developing critical thinking skills in mathematics

Check Out the New Website Shop!

Novels & Picture Books

Anchor Charts

• Critical Thinking

How To Encourage Critical Thinking in Math

By Mary Montero

Share This Post:

• Facebook Share
• Twitter Share
• Pinterest Share
• Email Share

Critical thinking is more than just a buzzword… It’s an essential skill that helps students develop problem-solving abilities and make logical connections between different concepts. By encouraging critical thinking in math, students learn to approach problems more thoughtfully, they learn to analyze and evaluate math concepts, identify patterns and relationships, and explore different strategies for finding the solution. Critical thinking also involves a great deal of persistence. Those are critical life skills!

When you think about it, students are typically asked to solve math problems and find the answer. Showing their work is frequently stressed too, which is important, but not the end. Instead, students need to be able to look at math in different ways in order to truly grasp a complete understanding of math concepts. Mathematics requires logical reasoning, problem-solving, and abstract thinking.

What Does Critical Thinking in Math Look Like?

When I think about critical thinking in math, I focus on:

• Solving problems through logical thinking . Students learn how to break down complex problems, analyze the different parts, and understand how they fit together logically.
• Identifying patterns and making connections. Students learn how to identify patterns across different math concepts, make connections between seemingly unrelated topics, and develop a more in-depth understanding of how math works.
• Evaluating and comparing solutions. Students learn to evaluate which solution is best for a given problem and identify any flaws in their reasoning or others’ reasoning when looking at different solutions

Mathematician Posters

These FREE Marvelous Mathematician posters have been a staple in my classroom for the last 8+ years! I first started using a version from MissMathDork and adapted them for my classroom over the years. 

I print, laminate, and add magnetic stickers on the back. At the beginning of the year, I only put one or two up at a time depending on our area of focus. Now, they are all hanging on my board, and I’ll pull out different ones depending on our area of focus. They are so empowering to my mathematicians and help them stay on track!

A Marvelous Mathematician:

• knows that quicker doesn’t mean better
• looks for patterns
• knows mistakes happen and keeps going
• makes sense of the most important details
• embraces challenges and works through frustrations
• uses proper math vocabulary to explain their thinking
• shows their work and models their thinking
• discusses solutions and evaluates reasonableness
• gives context by labeling answers
• applies mathematical knowledge to similar situations
• checks for errors (computational and conceptual)

Critical Thinking Math Activities

Here are a few of my favorite critical thinking activities. 

Square Of Numbers

I love to incorporate challenge problems (use Nrich and Openmiddle to get started) because they teach my students so much more than how to solve a math problem. They learn important lessons in teamwork, persistence, resiliency, and growth mindset. We talk about strategies for tackling difficult problems and the importance of not giving up when things get hard.

This square of numbers challenge was a hit!

ALL kids need to feel and learn to embrace challenge. Oftentimes, kids I see have rarely faced an academic challenge. Things have just come easy to them, so when it doesn’t, they can lack strategies that will help them. In fact, they will often give up before they even get started.

I tell them it’s my job to make sure I’m helping them stretch and grow their brain by giving them challenges. They don’t love it at first, but they eventually do! 

This domino challenge was another one from Nrich . I’m always on the hunt for problems like this!!  How would you guide students toward an answer??

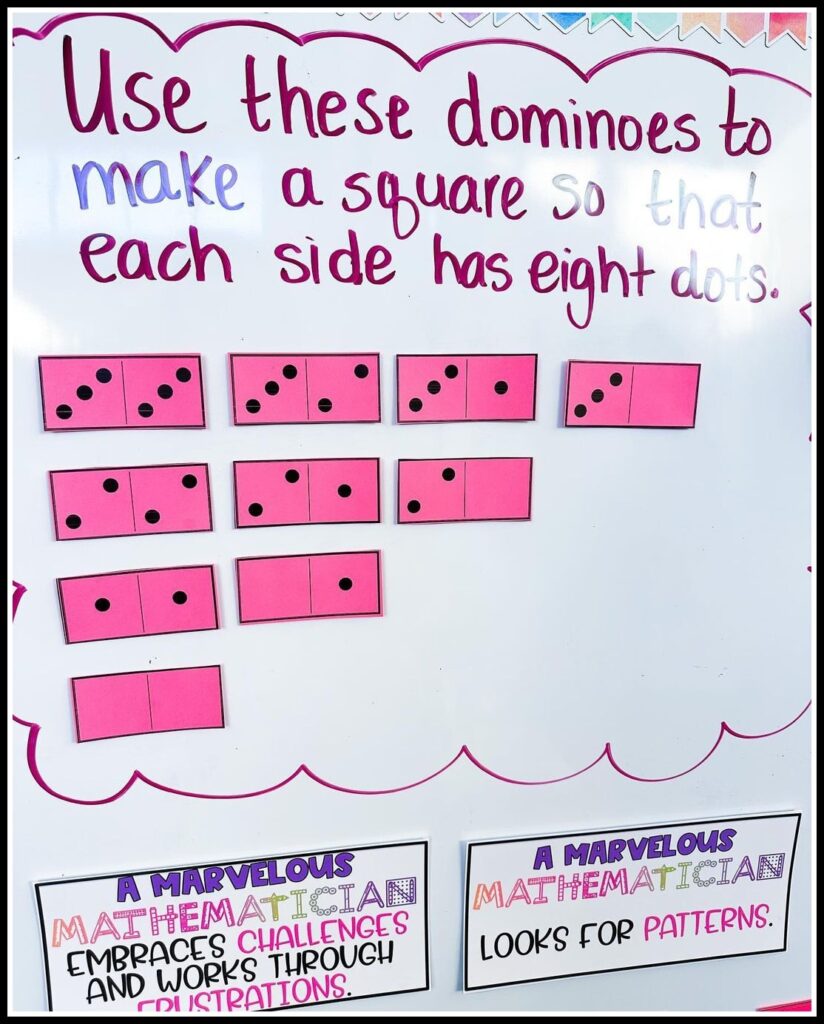
Fifteen Cards

This is a well-loved math puzzle with my students, and it’s amazing for encouraging students to consider all options when solving a math problem.

We have number cards 1-15 (one of each number) and only seven are laid out. With the given clues, students need to figure out which seven cards should be put out and in what order. My students love these, and after they’ve done a few, they enjoy creating their own, too! Use products, differences, and quotients to increase the challenge.

This is also adapted from Nrich, which is an AMAZING resource for math enrichment!

This is one of my favorite fraction lessons that I’ve done for years! Huge shout out to Meg from The Teacher Studio for this one. I give each child a slip of paper with this figure and they have to silently write their answer and justification. Then I tally up the answers and have students take a side and DEBATE with their reasoning! It’s an AMAZING conversation, and I highly recommend trying it with your students. 

Sometimes we leave it hanging overnight and work on visual models to make some proofs. 

Logic Puzzles

Logic puzzles are always a hit too! You can enrich and extend your math lessons with these ‘Math Mystery’ logic puzzles that are the perfect challenge for 4th, 5th, and 6th grades. The puzzles are skills-based, so they integrate well with almost ANY math lesson. You can use them to supplement instruction or challenge your fast-finishers and gifted students… all while encouraging critical thinking about important math skills!

Three levels are included, so they’re perfect to use for differentiation.

• Introductory logic puzzles are great for beginners (4th grade and up!)
• Advanced logic puzzles are great for students needing an extra challenge
• Extra Advanced logic puzzles are perfect for expert solvers… we dare you to figure these puzzles out! 

Do you have a group of students who are ready for more of a fraction challenge? My well-loved fraction puzzlers are absolutely perfect for fraction enrichment. They’ll motivate your students to excel at even the most challenging tasks! 

Math Projects

Math projects are another way to differentiation while building critical thinking skills. Math projects hold so much learning power with their real-world connections, differentiation options, collaborative learning opportunities, and numerous avenues for cross curricular learning too. 

If you’re new to math projects, I shared my best tips and tricks for using math projects in this blog post . They’re perfect for cumulative review, seasonal practice, centers, early finisher work, and more.

I use both concept-based math projects to focus on specific standards and seasonal math projects that integrate several skills.

Error Analysis

Finally, error analysis is always a challenging way to encourage critical thinking. When we use error analysis, we encourage students to analyze their own mistakes to prevent making the same mistakes in the future.

For my gifted students, I use error analysis tasks as an assessment when they have shown mastery of a unit during other tasks. For students in the regular classroom needing enrichment, I usually have them complete the tasks in a center or with a partner.

For students needing extra support, we complete error analysis in small groups.  We go step-by-step through the concept and they are always able to eventually identify what the error is. It is so empowering to students when they finally figure out the error AND it helps prevent them from making the same error in the future!

My FREE addition error analysis is a good place to start, no matter the grade level. I show them the process of walking through the problem and how best to complete an error analysis task.

When you’re ready for more, this bundle of error analysis tasks contains more than 240 tasks to engage and enrich your students in critical thinking practice.

If you want to dig even deeper, visit this conceptual vs computational error analysis post to learn more about using error analysis in the classroom. 

Related Critical Thinking Posts

• How to Increase Critical Thinking and Creativity in Your “Spare” Time
• More Tips to Increase Critical Thinking

Critical thinking is essential for students to develop a deeper understanding of math concepts, problem-solving skills, and a stronger ability to reason logically. When you learn how to encourage critical thinking in math, you’re setting your students up for success not only in more advanced math subjects they’ll encounter, but also in life. 

How do you integrate critical thinking in your classroom? Come share your ideas with us in our FREE Inspired In Upper Elementary Facebook group .

Mary Montero

I’m so glad you are here. I’m a current gifted and talented teacher in a small town in Colorado, and I’ve been in education since 2009. My passion (other than my family and cookies) is for making teachers’ lives easier and classrooms more engaging.

You might also like…

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

One Comment

Mary Thankyou for your inspirational activities. I have just read and loved the morning talk activities. I do have meetings with my students but usually at end of day. What time do you

©2023 Teaching With a Mountain View . All Rights Reserved | Designed by Ashley Hughes

Username or Email Address

Remember Me

Lost your password?

Review Cart

No products in the cart.

How to Improve Problem-Solving Skills: Mathematics and Critical Thinking

In today’s rapidly changing world, problem-solving has become a quintessential skill. When we discuss the topic, it’s natural to ask, “What is problem-solving?” and “How can we enhance this skill, particularly in children?” The discipline of mathematics offers a rich platform to explore these questions. Through math, not only do we delve into numbers and equations, but we also explore how to improve problem-solving skills and how to develop critical thinking skills in math. Let’s embark on this enlightening journey together.

What is Problem-Solving?

At its core, problem-solving involves identifying a challenge and finding a solution. But it’s not always as straightforward as it sounds. So, what is problem-solving? True problem-solving requires a combination of creative thinking and logical reasoning. Mathematics, in many ways, embodies this blend. When a student approaches a math problem, they must discern the issue at hand, consider various methods to tackle it, and then systematically execute their chosen strategy.

But what is problem-solving in a broader context? It’s a life skill. Whether we’re deciding the best route to a destination, determining how to save for a big purchase, or even figuring out how to fix a broken appliance, we’re using problem-solving.

How to Develop Critical Thinking Skills in Math

Critical thinking goes hand in hand with problem-solving. But exactly how to develop critical thinking skills in math might not be immediately obvious. Here are a few strategies:

• Contextual Learning: Teaching math within a story or real-life scenario makes it relevant. When students see math as a tool to navigate the world around them, they naturally begin to think critically about solutions.
• Open-ended Questions: Instead of merely seeking the “right” answer, encourage students to explain their thought processes. This nudges them to think deeply about their approach.
• Group Discussions: Collaborative learning can foster different perspectives, prompting students to consider multiple ways to solve a problem.
• Challenging Problems: Occasionally introducing problems that are a bit beyond a student’s current skill level can stimulate critical thinking. They will have to stretch their understanding and think outside the box.

What are the Six Basic Steps of the Problem-Solving Process?

Understanding how to improve problem-solving skills often comes down to familiarizing oneself with the systematic approach to challenges. So, what are the six basic steps of the problem-solving process?

• Identification: Recognize and define the problem.
• Analysis: Understand the problem’s intricacies and nuances.
• Generation of Alternatives: Think of different ways to approach the challenge.
• Decision Making: Choose the most suitable method to address the problem.
• Implementation: Put the chosen solution into action.
• Evaluation: Reflect on the solution’s effectiveness and learn from the outcome.

By embedding these steps into mathematical education, we provide students with a structured framework. When they wonder about how to improve problem-solving skills or how to develop critical thinking skills in math, they can revert to this process, refining their approach with each new challenge.

Making Math Fun and Relevant

At Wonder Math, we believe that the key to developing robust problem-solving skills lies in making math enjoyable and pertinent. When students see math not just as numbers on a page but as a captivating story or a real-world problem to be solved, their engagement skyrockets. And with heightened engagement comes enhanced understanding.

As educators and parents, it’s crucial to continuously ask ourselves: how can we demonstrate to our children what problem-solving is? How can we best teach them how to develop critical thinking skills in math? And how can we instill in them an understanding of the six basic steps of the problem-solving process?

The answer, we believe, lies in active learning, contextual teaching, and a genuine passion for the beauty of mathematics.

The Underlying Beauty of Mathematics

Often, people perceive mathematics as a rigid discipline confined to numbers and formulas. However, this is a limited view. Math, in essence, is a language that describes patterns, relationships, and structures. It’s a medium through which we can communicate complex ideas, describe our universe, and solve intricate problems. Understanding this deeper beauty of math can further emphasize how to develop critical thinking skills in math.

Why Mathematics is the Ideal Playground for Problem-Solving

Math provides endless opportunities for problem-solving. From basic arithmetic puzzles to advanced calculus challenges, every math problem offers a chance to hone our problem-solving skills. But why is mathematics so effective in this regard?

• Structured Challenges: Mathematics presents problems in a structured manner, allowing learners to systematically break them down. This format mimics real-world scenarios where understanding the structure of a challenge can be half the battle.
• Multiple Approaches: Most math problems can be approached in various ways . This teaches learners flexibility in thinking and the ability to view a single issue from multiple angles.
• Immediate Feedback: Unlike many real-world problems where solutions might take time to show results, in math, students often get immediate feedback. They can quickly gauge if their approach works or if they need to rethink their strategy.

Enhancing the Learning Environment

To genuinely harness the power of mathematics in developing problem-solving skills, the learning environment plays a crucial role. A student who is afraid of making mistakes will hesitate to try out different approaches, stunting their critical thinking growth.

However, in a nurturing, supportive environment where mistakes are seen as learning opportunities, students thrive. They become more willing to take risks, try unconventional solutions, and learn from missteps. This mindset, where failure is not feared but embraced as a part of the learning journey, is pivotal for developing robust problem-solving skills.

Incorporating Technology

In our digital age, technology offers innovative ways to explore math. Interactive apps and online platforms can provide dynamic problem-solving scenarios, making the process even more engaging. These tools can simulate real-world challenges, allowing students to apply their math skills in diverse contexts, further answering the question of how to improve problem-solving skills.

More than Numbers 

In summary, mathematics is more than just numbers and formulas—it’s a world filled with challenges, patterns, and beauty. By understanding its depth and leveraging its structured nature, we can provide learners with the perfect platform to develop critical thinking and problem-solving skills. The key lies in blending traditional techniques with modern tools, creating a holistic learning environment that fosters growth, curiosity, and a lifelong love for learning.

Join us on this transformative journey at Wonder Math. Let’s make math an adventure, teaching our children not just numbers and equations, but also how to improve problem-solving skills and navigate the world with confidence. Enroll your child today and witness the magic of mathematics unfold before your eyes!

FAQ: Mathematics and Critical Thinking

1. what is problem-solving in the context of mathematics.

Problem-solving in mathematics refers to the process of identifying a mathematical challenge and systematically working through methods and strategies to find a solution.

2. Why is math considered a good avenue for developing problem-solving skills?

Mathematics provides structured challenges and allows for multiple approaches to find solutions. This promotes flexibility in thinking and encourages learners to view problems from various angles.

3. How does contextual learning enhance problem-solving abilities?

By teaching math within a story or real-life scenario, it becomes more relevant for the learner. This helps them see math as a tool to navigate real-world challenges , thereby promoting critical thinking.

4. What are the six basic steps of the problem-solving process in math?

The six steps are: Identification, Analysis, Generation of Alternatives, Decision Making, Implementation, and Evaluation.

5. How can parents support their children in developing mathematical problem-solving skills?

Parents can provide real-life contexts for math problems , encourage open discussions about different methods, and ensure a supportive environment where mistakes are seen as learning opportunities.

6. Are there any tools or apps that can help in enhancing problem-solving skills in math?

Yes, there are various interactive apps and online platforms designed specifically for math learning. These tools provide dynamic problem-solving scenarios and simulate real-world challenges, making the learning process engaging.

7. How does group discussion foster critical thinking in math?

Group discussions allow students to hear different perspectives and approaches to a problem. This can challenge their own understanding and push them to think about alternative methods.

8. Is it necessary to always follow the six steps of the problem-solving process sequentially?

While the six steps provide a structured approach, real-life problem-solving can sometimes be more fluid. It’s beneficial to know the steps, but adaptability and responsiveness to the situation are also crucial.

9. How does Wonder Math incorporate active learning in teaching mathematics?

Wonder Math integrates mathematics within engaging stories and real-world scenarios, making it fun and relevant. This active learning approach ensures that students are not just passive recipients but active participants in the learning process.

10. What if my child finds a math problem too challenging and becomes demotivated?

It’s essential to create a supportive environment where challenges are seen as growth opportunities. Remind them that every problem is a chance to learn, and it’s okay to seek help or approach it differently.

Related posts

Summer Math Programs: How They Can Prevent Learning Loss in Young Students

As summer approaches, parents and educators alike turn their attention to how they can support young learners during the break. Summer is a time for relaxation, fun, and travel, yet it’s also a critical period when learning loss can occur. This phenomenon, often referred to as the “summer slide,” impacts students’ progress, especially in foundational subjects like mathematics. It’s reported…

Math Programs 101: What Every Parent Should Know When Looking For A Math Program

  As a parent, you know that a solid foundation in mathematics is crucial for your child’s success, both in school and in life. But with so many math programs and math help services out there, how do you choose the right one? Whether you’re considering Outschool classes, searching for “math tutoring near me,” or exploring tutoring services online, understanding…