Word Problems on Fraction
In word problems on fraction we will solve different types of problems on multiplication of fractional numbers and division of fractional numbers.

I. Word Problems on Addition of Fractions:
1. Nairitee took \(\frac{7}{8}\) hour to paint a table and \(\frac{2}{3}\) hour to paint a chair. How much time did he take in painting both items?
Total time taken in painting both items = \(\frac{7}{8}\) h + \(\frac{2}{3}\) h = (\(\frac{7}{8}\) + \(\frac{2}{3}\)) h
= (\(\frac{21 + 16}{24}\)) h
= \(\frac{37}{24}\) h
= 1\(\frac{13}{24}\) h
Therefore, Nairitee took 1\(\frac{13}{24}\) hours in painting both items.
2. Nitheeya and Nairitee \(\frac{3}{10}\) and \(\frac{1}{6}\) of a cake respectively. What portion of the cake did they eat together?
The portion of cake ate by Nitheeya = \(\frac{3}{10}\)
The portion of cake ate by Nitheeya = \(\frac{1}{6}\) The portion they ate together = \(\frac{3}{10}\) + \(\frac{1}{6}\)
= \(\frac{9}{30}\) + \(\frac{5}{30}\); [Since, LCM of 10 and 6 = 30]
= \(\frac{9 + 5}{30}\)
= \(\frac{14}{30}\)
= \(\frac{7}{15}\)
Therefore, together Nitheeya and Nairitee ate \(\frac{7}{15}\) of the cake.
3. Rachel took \(\frac{1}{2}\) hour to paint a table and \(\frac{1}{3}\) hour to paint a chair. How much time did she take in all?
II. Word Problems on Subtraction of Fractions:
1. Out of \(\frac{12}{17}\) m of cloth given to a tailor, \(\frac{1}{5}\) m were used. Find the length of cloth unused.
Length of the cloth given to the tailors = \(\frac{12}{17}\) m
Length of cloth used = \(\frac{1}{5}\) m
Length of the unused cloth = \(\frac{12}{17}\) m - \(\frac{1}{5}\) m
= (\(\frac{12}{17}\) - \(\frac{1}{5}\)) m
= (\(\frac{12 × 5}{17 × 5}\) - \(\frac{1 × 17}{5 × 17}\)) m; [Since, LCM of 17 and 5 = 85]
= (\(\frac{60}{85}\) - \(\frac{17}{85}\)) m
= (\(\frac{60 - 17}{85}\) m
= (\(\frac{43}{85}\) m
2. Nairitee has $6\(\frac{4}{7}\). She gives $4\(\frac{2}{3}\) to her mother. How much money does she have now?
Money with Nairitee = $6\(\frac{4}{7}\)
Money given to her mother = $4\(\frac{2}{3}\)
Money left with Nairitee = $6\(\frac{4}{7}\) - $4\(\frac{2}{3}\)
= $(6\(\frac{4}{7}\) - 4\(\frac{2}{3}\))
= $(\(\frac{46}{7}\) - \(\frac{14}{3}\))
= $(\(\frac{46 × 3}{7 × 3}\) - \(\frac{14 × 7}{3 × 7}\)) ; [Since, LCM of 7 and 3 = 21]
= $(\(\frac{138}{21}\) - \(\frac{98}{21}\))
= $\(\frac{40}{21}\)
= $1\(\frac{19}{21}\)
Therefore, Nairitee has $1\(\frac{19}{21}\).
3. If 3\(\frac{1}{2}\) m of wire is cut from a piece of 10 m long wire, how much of wire is left?
Total length of the wire = 10 m
Fraction of the wire cut out = 3\(\frac{1}{2}\) m = \(\frac{7}{2}\) m
Length of the wire left = 10 m – 3\(\frac{1}{2}\) m
= [\(\frac{10}{1}\) - \(\frac{7}{2}\)] m, [L.C.M. of 1, 2 is 2]
= [\(\frac{20}{2}\) - \(\frac{7}{2}\)] m, [\(\frac{10}{1}\) × \(\frac{2}{2}\)]
= [\(\frac{20 - 7}{2}\)] m
= \(\frac{13}{2}\) m
= 6\(\frac{1}{2}\) m
III. Word Problems on Multiplication of Fractions:
1. \(\frac{4}{7}\) of a number is 84. Find the number. Solution: According to the problem, \(\frac{4}{7}\) of a number = 84 Number = 84 × \(\frac{7}{4}\) [Here we need to multiply 84 by the reciprocal of \(\frac{4}{7}\)]
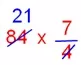
= 21 × 7 = 147 Therefore, the number is 147.
2. One half of the students in a school are girls, \(\frac{3}{5}\) of these girls are studying in lower classes. What fraction of girls are studying in lower classes?
Fraction of girls studying in school = \(\frac{1}{2}\)
Fraction of girls studying in lower classes = \(\frac{3}{5}\) of \(\frac{1}{2}\)
= \(\frac{3}{5}\) × \(\frac{1}{2}\)
= \(\frac{3 × 1}{5 × 2}\)
= \(\frac{3}{10}\)
Therefore, \(\frac{3}{10}\) of girls studying in lower classes.
3. Maddy reads three-fifth of 75 pages of his lesson. How many more pages he need to complete the lesson? Solution: Maddy reads = \(\frac{3}{5}\) of 75 = \(\frac{3}{5}\) × 75
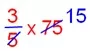
= 45 pages. Maddy has to read = 75 – 45. = 30 pages. Therefore, Maddy has to read 30 more pages.
IV. Word Problems on Division of Fractions:
1. A herd of cows gives 4 litres of milk each day. But each cow gives one-third of total milk each day. They give 24 litres milk in six days. How many cows are there in the herd?
Solution: A herd of cows gives 4 litres of milk each day. Each cow gives one-third of total milk each day = \(\frac{1}{3}\) of 4 Therefore, each cow gives \(\frac{4}{3}\) of milk each day. Total no. of cows = 4 ÷ \(\frac{4}{3}\) = 4 × \(\frac{3}{4}\) = 3 Therefore there are 3 cows in the herd.
Worksheet on Word problems on Fractions:
1. Shelly walked \(\frac{1}{3}\) km. Kelly walked \(\frac{4}{15}\) km. Who walked farther? How much farther did one walk than the other?
2. A frog took three jumps. The first jump was \(\frac{2}{3}\) m long, the second was \(\frac{5}{6}\) m long and the third was \(\frac{1}{3}\) m long. How far did the frog jump in all?
3. A vessel contains 1\(\frac{1}{2}\) l of milk. John drinks \(\frac{1}{4}\) l of milk; Joe drinks \(\frac{1}{2}\) l of milk. How much of milk is left in the vessel?
4. Between 4\(\frac{2}{3}\)and 3\(\frac{2}{3}\) which is greater and by how much?
5. What must be subtracted from 5\(\frac{1}{6}\) to get 2\(\frac{1}{8}\)?
You might like these
Conversion of Mixed Fractions into Improper Fractions |Solved Examples
To convert a mixed number into an improper fraction, we multiply the whole number by the denominator of the proper fraction and then to the product add the numerator of the fraction to get the numerator of the improper fraction. I

Types of Fractions |Proper Fraction |Improper Fraction |Mixed Fraction
The three types of fractions are : Proper fraction, Improper fraction, Mixed fraction, Proper fraction: Fractions whose numerators are less than the denominators are called proper fractions. (Numerator < denominator). Two parts are shaded in the above diagram.

5th Grade Fractions | Definition | Examples | Word Problems |Worksheet
In 5th Grade Fractions we will discuss about definition of fraction, concept of fractions and different types of examples on fractions. A fraction is a number representing a part of a whole. The whole may be a single object or a group of objects.

Conversion of Improper Fractions into Mixed Fractions |Solved Examples
In conversion of improper fractions into mixed fractions, we follow the following steps: Step I: Obtain the improper fraction. Step II: Divide the numerator by the denominator and obtain the quotient and remainder. Step III: Write the mixed fraction

Equivalent Fractions | Fractions |Reduced to the Lowest Term |Examples
The fractions having the same value are called equivalent fractions. Their numerator and denominator can be different but, they represent the same part of a whole. We can see the shade portion with respect to the whole shape in the figures from (i) to (viii) In; (i) Shaded

Subtraction of Fractions having the Same Denominator | Like Fractions
To find the difference between like fractions we subtract the smaller numerator from the greater numerator. In subtraction of fractions having the same denominator, we just need to subtract the numerators of the fractions.


Comparison of Like Fractions | Comparing Fractions | Like Fractions
Any two like fractions can be compared by comparing their numerators. The fraction with larger numerator is greater than the fraction with smaller numerator, for example \(\frac{7}{13}\) > \(\frac{2}{13}\) because 7 > 2. In comparison of like fractions here are some

Comparison of Fractions having the same Numerator|Ordering of Fraction
In comparison of fractions having the same numerator the following rectangular figures having the same lengths are divided in different parts to show different denominators. 3/10 3/5 > 3/10 In the fractions having the same numerator, that fraction is

Worksheet on Comparison of Like Fractions | Greater & Smaller Fraction
In worksheet on comparison of like fractions, all grade students can practice the questions on comparison of like fractions. This exercise sheet on comparison of like fractions can be practiced
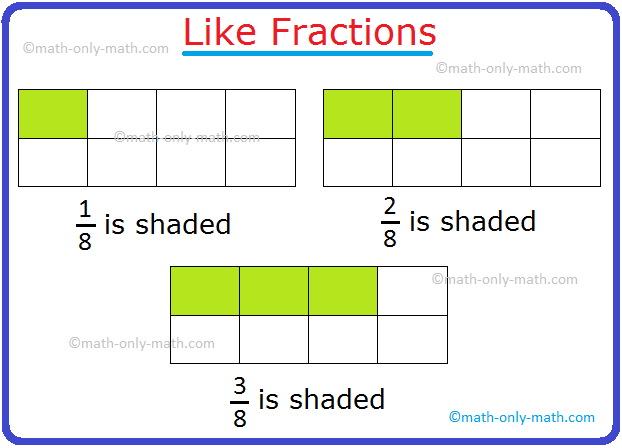
Like and Unlike Fractions | Like Fractions |Unlike Fractions |Examples
Like and unlike fractions are the two groups of fractions: (i) 1/5, 3/5, 2/5, 4/5, 6/5 (ii) 3/4, 5/6, 1/3, 4/7, 9/9 In group (i) the denominator of each fraction is 5, i.e., the denominators of the fractions are equal. The fractions with the same denominators are called
● Multiplication is Repeated Addition.
● Multiplication of Fractional Number by a Whole Number.
● Multiplication of a Fraction by Fraction.
● Properties of Multiplication of Fractional Numbers.
● Multiplicative Inverse.
● Worksheet on Multiplication on Fraction.
● Division of a Fraction by a Whole Number.
● Division of a Fractional Number.
● Division of a Whole Number by a Fraction.
● Properties of Fractional Division.
● Worksheet on Division of Fractions.
● Simplification of Fractions.
● Worksheet on Simplification of Fractions.
● Word Problems on Fraction.
● Worksheet on Word Problems on Fractions.
5th Grade Numbers
5th Grade Math Problems
From Word Problems on Fraction to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy

Recent Articles
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Dec 13, 24 08:43 AM
Patterns in Math | Missing Number | Counting Numbers | Worksheets
Dec 13, 24 12:31 AM
Concept of Pattern | Similar Patterns in Mathematics | Similar Pattern
Dec 12, 24 11:22 PM
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 12, 24 10:31 PM
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Child Login
- Kindergarten
- Number charts
- Skip Counting
- Place Value
- Number Lines
- Subtraction
- Multiplication
- Word Problems
- Comparing Numbers
- Ordering Numbers
- Odd and Even
- Prime and Composite
- Roman Numerals
- Ordinal Numbers
- In and Out Boxes
- Number System Conversions
- More Number Sense Worksheets
- Size Comparison
- Measuring Length
- Metric Unit Conversion
- Customary Unit Conversion
- Temperature
- More Measurement Worksheets
- Writing Checks
- Profit and Loss
- Simple Interest
- Compound Interest
- Tally Marks
- Mean, Median, Mode, Range
- Mean Absolute Deviation
- Stem-and-leaf Plot
- Box-and-whisker Plot
- Permutation and Combination
- Probability
- Venn Diagram
- More Statistics Worksheets
- Shapes - 2D
- Shapes - 3D
- Lines, Rays and Line Segments
- Points, Lines and Planes
- Transformation
- Quadrilateral
- Ordered Pairs
- Midpoint Formula
- Distance Formula
- Parallel, Perpendicular and Intersecting Lines
- Scale Factor
- Surface Area
- Pythagorean Theorem
- More Geometry Worksheets
- Converting between Fractions and Decimals
- Significant Figures
- Convert between Fractions, Decimals, and Percents
- Proportions
- Direct and Inverse Variation
- Order of Operations
- Squaring Numbers
- Square Roots
- Scientific Notations
- Speed, Distance, and Time
- Absolute Value
- More Pre-Algebra Worksheets
- Translating Algebraic Phrases
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
- Algebraic Identities
- Quadratic Equations
- Systems of Equations
- Polynomials
- Inequalities
- Sequence and Series
- Complex Numbers
- More Algebra Worksheets
- Trigonometry
- Math Workbooks
- English Language Arts
- Summer Review Packets
- Social Studies
- Holidays and Events
- Worksheets >
- Pre-Algebra >
- Fractions >
- Addition >
Fraction Addition Word Problems Worksheets
Let children work on our printable adding fractions word problems worksheets hammer and tongs! Whether it's sharing a meal with your friends or measuring the ingredients for a recipe, adding fractions is at the heart of it all, hence our worksheets. A wealth of real-life scenarios that involve addition of fractions with whole numbers and addition of two like fractions, two unlike fractions, and two mixed numbers, our pdf worksheets are indispensable for grade 3, grade 4, grade 5, and grade 6 students. The free fraction addition word problems worksheet is worth a try!

Adding Fractions with Whole Numbers
Dazzle 3rd grade kids with a gift of lifelike story problems! If you're a novice up against fraction addition, don't miss our pdf adding fractions word problems worksheets using whole numbers and fractions!
- Download the set

Adding Like Fractions Word Problems
Gerald ate 5/9 of an apple, and Garry ate 4/9 of it. How many apples did they eat in all? Good going! They both ate one whole apple. Simply combine the numerators and solve the like fraction word problems here!

Adding Unlike Fractions
A potpourri of word problems that involve adding unlike fractions, these pdfs mean that 4th grade and 5th grade students will breeze through addition of fractions with different denominators in their day-to-day lives.

Adding Mixed Numbers | Same Denominators
See in your mind's eye adding mixed numbers with same denominators riding on the several real-life scenarios in our printable worksheets! Convert the mixed numbers to fractions, and add them as usual.

Adding Mixed Numbers | Different Denominators
Steal a march on your 5th grade and 6th grade peers by getting your act together to power through the real-world situations featured in this set of printable adding mixed numbers word problems worksheets.
Related Worksheets
» Adding Like Fractions
» Adding Unlike Fractions
» Adding Mixed Numbers
» Adding Fractions with Whole Numbers
» Fraction Word Problems
Become a Member
Membership Information
Printing Help
How to Use Online Worksheets
How to Use Printable Worksheets
Privacy Policy
Terms of Use
Copyright © 2024 - Math Worksheets 4 Kids
This is a members-only feature!


IMAGES
VIDEO