network capacity assignment problem

Network flow problem

Author: Aaron Wheeler, Chang Wei, Cagla Deniz Bahadir, Ruobing Shui, Ziqiu Zhang (ChemE 6800 Fall 2020)

1 Introduction
2.1.1 The Assignment Problem
2.1.2 The Transportation Problem
2.1.3 The Shortest-Path Problem
2.1.4 Maximal Flow Problem
2.2.1 Ford–Fulkerson Algorithm
3.1 Formulation of the Problem
3.2 Solution of the Problem
4.1 The Minimum Cost Flow Problem
4.2 The Assignment Problem
4.3 The Shortest Path Problem
5 Conclusion
6 References

Introduction

Network flow problems arise in several key instances and applications within society and have become fundamental problems within computer science, operations research, applied mathematics, and engineering. Developments in the approach to tackle these problems resulted in algorithms that became the chief instruments for solving problems related to large-scale systems and industrial logistics. Spurred by early developments in linear programming, the methods for addressing these extensive problems date back several decades and they evolved over time as the use of digital computing became increasingly prevalent in industrial processes. Historically, the first instance of an algorithmic development for the network flow problem came in 1956, with the network simplex method formulated by George Dantzig. [1] A variation of the simplex algorithm that revolutionized linear programming, this method leveraged the combinatorial structure inherent to these types of problems and demonstrated incredibly high accuracy. [2] This method and its variations would go on to define the embodiment of the algorithms and models for the various and distinct network flow problems discussed here.

Theory, Methodology, and Algorithms

$X$

Additional constraints of the network flow optimization model place limits on the solution and vary significantly based on the specific type of problem being solved. Historically, the classic network flow problems are considered to be the maximum flow problem and the minimum-cost circulation problem, the assignment problem, bipartite matching problem, transportation problem, and the transshipment problem. [2] The approach to these problems become quite specific based upon the problem’s objective function but can be generalized by the following iterative approach: 1. determining the initial basic feasible solution; 2. checking the optimality conditions (i.e. whether the problem is infeasible, unbounded over the feasible region, optimal solution has been found, etc.); and 3. constructing an improved basic feasible solution if the optimal solution has not been determined. [3]

General Applications

The assignment problem.

Various real-life instances of assignment problems exist for optimization, such as assigning a group of people to different tasks, events to halls with different capacities, rewards to a team of contributors, and vacation days to workers. All together, the assignment problem is a bipartite matching problem in the kernel. [3] In a classical setting, two types of objects of equal amount are bijective (i.e. they have one-to-one matching), and this tight constraint ensures a perfect matching. The objective is to minimize the cost or maximize the profit of matching, since different items of two types have distinct affinity.

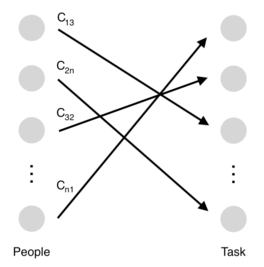
Figure 2 can be viewed as a network. The nodes represent people and tasks, and the edges represent potential assignments between a person and a task. Each task can be completed by any person. However, the person that actually ends up being assigned to the task will be the lone individual who is best suited to complete. In the end, the edges with positive flow values will be the only ones represented in the finalized assignment. [5]

$x_{ij}$

The concise-form formulation of the problem is as follows [3] :

$z=\sum _{i=1}^{n}\sum _{j=1}^{n}c_{ij}x_{ij}$

Subject to:

$\sum _{j=1}^{n}x_{ij}=1~~\forall i\in [1,n]$

The first constraint captures the requirement of assigning each person to a single task. The second constraint indicates that each task must be done by exactly one person. The objective function sums up the overall benefits of all assignments.

To see the analogy between the assignment problem and the network flow, we can describe each person supplying a flow of 1 unit and each task demanding a flow of 1 unit, with the benefits over all “channels” being maximized. [3]

A potential issue lies in the branching of the network, specifically an instance where a person splits its one unit of flow into multiple tasks and the objective remains maximized. This shortcoming is allowed by the laws that govern the network flow model, but are unfeasible in real-life instances. Fortunately, since the network simplex method only involves addition and subtraction of a single edge while transferring the basis, which is served by the spanning tree of the flow graph, if the supply (the number of people here) and the demand (the number of tasks here) in the constraints are integers, the solved variables will be automatically integers even if it is not explicitly stated in the problem. This is called the integrality of the network problem, and it certainly applies to the assignment problem. [6]

The Transportation Problem

People first came up with the transportation problem when distributing troops during World War II. [7] Now, it has become a useful model for solving logistics problems, and the objective is usually to minimize the cost of transportation.

Consider the following scenario:

$M$

Several quantities should be defined to help formulate the frame of the solution:

$S_{i}$

Here, the amount of material being delivered and being consumed is bound to the supply and demand constraints:

$\sum _{j}^{n}x_{ij}\ \leq S_{i}\qquad \forall i\in I=[1,m]$

The objective is to find the minimum cost of transportation, so the cost of each transportation line should be added up, and the total cost should be minimized.

$\sum _{i}^{m}\sum _{j}^{n}x_{ij}\ C_{ij}$

Using the definitions above, the problem can be formulated as such:

$\quad z=\sum _{i}^{m}\sum _{j}^{n}x_{ij}\ C_{ij}$

The problem and the formulation is adapted from Chapter 8 of the book: Applied Mathematical Programming by Bradley, Hax and Magnanti. [3]

The Shortest-Path Problem

The shortest-path problem can be defined as finding the path that yields the shortest total distance between the origin and the destination. Each possible stop is a node and the paths between these nodes are edges incident to these nodes, where the path distance becomes the weight of the edges. In addition to being the most common and straightforward application for finding the shortest path, this model is also used in various applications depending on the definition of nodes and edges. [3] For example, when each node represents a different object and the edge specifies the cost of replacement, the equipment replacement problem is derived. Moreover, when each node represents a different project and the edge specifies the relative priority, the model becomes a project scheduling problem.

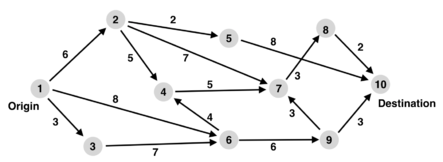
A graph of the general shortest-path problem is depicted as Figure 4:

$c_{12}$

The first term of the constraint is the total outflow of the node i, and the second term is the total inflow. So, the formulation above could be seen as one unit of flow being supplied by the origin, one unit of flow being demanded by the destination, and no net inflow or outflow at any intermediate nodes. These constraints mandate a flow of one unit, amounting to the active path, from the origin to the destination. Under this constraint, the objective function minimizes the overall path distance from the origin to the destination.

Similarly, the integrality of the network problem applies here, precluding the unreasonable fractioning. With supply and demand both being integer (one here), the edges can only have integer amount of flow in the result solved by simplex method. [6]

In addition, the point-to-point model above can be further extended to other problems. A number of real life scenarios require visiting multiple places from a single starting point. This “Tree Problem” can be modeled by making small adjustments to the original model. In this case, the source node should supply more units of flow and there will be multiple sink nodes demanding one unit of flow. Overall, the objective and the constraint formulation are similar. [4]

Maximal Flow Problem

This problem describes a situation where the material from a source node is sent to a sink node. The source and sink node are connected through multiple intermediate nodes, and the common optimization goal is to maximize the material sent from the source node to the sink node. [3]

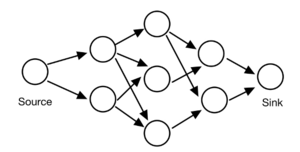
The given structure is a piping system. The water flows into the system from the source node, passing through the intermediate nodes, and flows out from the sink node. There is no limitation on the amount of water that can be used as the input for the source node. Therefore, the sink node can accept an unlimited amount of water coming into it. The arrows denote the valid channel that water can flow through, and each channel has a known flow capacity. What is the maximum flow that the system can take?

For the source and sink node, they have net flow that is non-zero:

${\textstyle m}$

Flow capacity definition is applied to all nodes (including intermediate nodes, the sink, and the source):

$C_{ab}$

The main constraints for this problem are the transport capacity between each node and the material conservation:

$0\leq x_{ab}\leq C_{ab}$

Overall, the net flow out of the source node has to be the same as the net flow into the sink node. This net flow is the amount that should be maximized.

Using the definitions above:

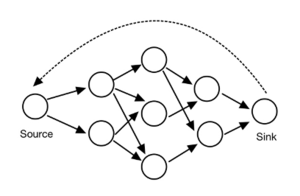
This expression can be further simplified by introducing an imaginary flow from the sink to the source.

By introducing this imaginary flow, the piping system is now closed. The mass conservation constraint now also holds for the source and sink node, so they can be treated as the intermediate nodes. The problem can be rewritten as the following:

$\quad z=x_{vu}$

The problem and the formulation are derived from an example in Chapter 8 of the book: Applied Mathematical Programming by Bradley, Hax and Magnanti. [3]

Ford–Fulkerson Algorithm

A broad range of network flow problems could be reduced to the max-flow problem. The most common way to approach the max-flow problem in polynomial time is the Ford-Fulkerson Algorithm (FFA). FFA is essentially a greedy algorithm and it iteratively finds the augmenting s-t path to increase the value of flow. The pathfinding terminates until there is no s-t path present. Ultimately, the max-flow pattern in the network graph will be returned. [8]

$0\leq f(e)\leq c_{e},\forall e\in E$

Numerical Example and Solution

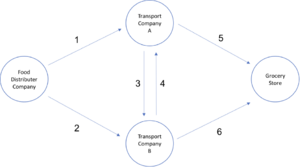
A Food Distributor Company is farming and collecting vegetables from farmers to later distribute to the grocery stores. The distributor has specific agreements with different third-party companies to mediate the delivery to the grocery stores. In a particular month, the company has 600 ton vegetables to deliver to the grocery store. They have agreements with two third-party transport companies A and B, which have different tariffs for delivering goods between themselves, the distributor, and the grocery store. They also have limits on transport capacity for each path. These delivery points are numbered as shown below, with path 1 being the transport from the Food Distributor Company to the transport company A. The limits and tariffs for each path can be found in the Table 2 below, and the possible transportation connections between the distributor company, the third-party transporters, and the grocery store are shown in the figure below. The distributor companies cannot hold any amount of food, and any incoming food should be delivered to an end point. The distributor company wants to minimize the overall transport cost of shipping 600 tons of vegetables to the grocery store by choosing the optimal path provided by the transport companies. How should the distributor company map out their path and the amount of vegetables carried on each path to minimize cost overall?

This question is adapted from one of the exercise questions in chapter 8 of the book: Applied Mathematical Programming by Bradley, Hax and Magnanti [3] .

Formulation of the Problem

$x_{1},x_{2},x_{3},...,x_{6}$

The second step is to write down the constraints. The first constraint ensures that the net amount present in the Transport Company A, which is the deliveries received from path 1 and path 2 minus the transport to Transport Company B should be delivered to the grocery store with path 5. The second constraint ensures this for the Transport Company B. The third and fourth constraints are ensuring that the total amount of vegetables shipping from the Food Distributor Company and the total amount of vegetables delivered to the grocery store are both 600 tons. The constraints 5 to 10 depict the upper limits of the amount of vegetables that can be carried on paths 1 to 6. The final constraint depicts that all variables are non-negative.

Solution of the Problem

This problem can be solved using Simplex Algorithm [11] or with the CPLEX Linear Programming solver in GAMS optimization platform. The steps of the solution using the GAMS platform is as follows:

variables x1,x2,x3,x4,x5,x6,z;

obj.. z=e= 10*x1+12.5*x2+5*x3+7.5*x4+10*x5+20*x6;

Overall, there are 10 constraints in this problem. The constraints 1, and 2 are equations for the paths 5 and 6. The amount carried in path 5 can be found by summing the amount of vegetables incoming to Transport Company A from path 1 and path 4, minus the amount of vegetables leaving Transport Company A with path 3. This can be attributed to the restriction that barrs the companies from keeping any vegetables and requires them to eventually deliver all the incoming produce. The equality 1 ensures that this constraint holds for path 5 and equation 2 ensures it for path 6. A sample of these constraints is written below for path 5:

c1.. x5 =e=x1-x3+x4;

Constraint 3 ensures that the sum of vegetables carried in path 1 and path 2 add to the total of 600 tons of vegetables that leave the Food Distributor Company. Likewise, the constraint 4 ensures that the sum amount of food transported in paths 5 and 6 adds up to 600 tons of vegetables that have to be delivered to the grocery store. A sample of these constraints is written below for the total delivery to the grocery store:

c3.. x5+x6=e=600;

Constraints 5 to 10 should ensure that the amount of food transported in each path should not exceed the maximum capacity depicted in the table. A sample of these constraints is written below for the capacity of path 1:

c5.. x1=l=250;

After listing the variables, objective function and the constraints, the final step is to call the CPLEX solver and set the type of the optimization problem as lp (linear programming). In this case the problem will be solved with a Linear Programming algorithm to minimize the objective (cost) function.

The GAMS code yields the results below:

x1 = 250, x2 = 350, x3 = 0, x4 = 50, x5 = 300, x6 = 300, z =16250.

Real Life Applications

Network problems have many applications in all kinds of areas such as transportation, city design, resource management and financial planning. [6]

There are several special cases of network problems, such as the shortest path problem, minimum cost flow problem, assignment problem and transportation problem. [6] Three application cases will be introduced here.

The Minimum Cost Flow Problem

Minimum cost flow problems are pervasive in real life, such as deciding how to allocate temporal quay crane in container terminals, and how to make optimal train schedules on the same railroad line. [12]

R. Dewil and his group use MCNFP to assist traffic enforcement. [13] Police patrol “hot spots”, which are areas where crashes occur frequently on highways. R. Dewil studies a method intended to estimate the optimal route of hot spots. He describes the time it takes to move the detector to a certain position as the cost, and the number of patrol cars from one node to next as the flow, in order to minimize the total cost. [13]

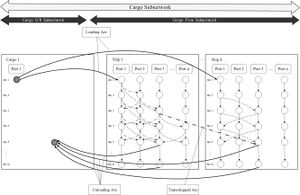
Dung-Ying Lin studies an assignment problem in which he aims to assign freights to ships and arrange transportation paths along the Northern Sea Route in a manner which yields maximum profit. [14] Within this network composed of a ship subnetwork and a cargo subnetwork( shown as Figure 12 and Figure 13), each node corresponds to a port at a specific time and each arc represents the movement of a ship or a cargo. Other types of assignment problems are faculty scheduling, freight assignment, and so on.

The Shortest Path Problem

Shortest path problems are also present in many fields, such as transportation, 5G wireless communication, and implantation of the global dynamic routing scheme. [15][16][17]

Qiang Tu and his group studies the constrained reliable shortest path (CRSP) problem for electric vehicles in the urban transportation network. [15] He describes the reliable travel time of path as the objective item, which is made up of planning travel time of path and the reliability item. The group studies the Chicago sketch network consisting of 933 nodes and 2950 links and the Sioux Falls network consisting of 24 nodes and 76 links. The results show that the travelers’ risk attitudes and properties of electric vehicles in the transportation network can have a great influence on the path choice. [15] The study can contribute to the invention of the city navigation system.

Since its inception, the network flow problem has provided humanity with a straightforward and scalable approach for several large-scale challenges and problems. The Simplex algorithm and other computational optimization platforms have made addressing these problems routine, and have greatly expedited efforts for groups concerned with supply-chain and other distribution processes. The formulation of this problem has had several derivations from its original format, but its overall methodology and approach have remained prevalent in several of society’s industrial and commercial processes, even over half a century later. Classical models such as the assignment, transportation, maximal flow, and shortest path problem configurations have found their way into diverse settings, ranging from streamlining oil distribution networks along the gulf coast to arranging optimal scheduling assignments for college students amidst a global pandemic. All in all, the network flow problem and its monumental impact, have made it a fundamental tool for any group that deals with combinatorial data sets. And with the surge in adoption of data-driven models and applications within virtually all industries, the use of the network flow problem approach will only continue to drive innovation and meet consumer demands for the foreseeable future.

1. Karp, R. M. (2008). George Dantzig’s impact on the theory of computation . Discrete Optimization, 5(2), 174-185.

2. Goldberg, A. V. Tardos, Eva, Tarjan, Robert E. (1989). Network Flow Algorithms, Algorithms and Combinatorics . 9. 101-164.

3. Bradley, S. P. Hax, A. C., & Magnanti, T. L. (1977). Network Models. Applied mathematical programming (p. 259). Reading, MA: Addison-Wesley.

4. Chinneck, J. W. (2006). Practical optimization: a gentle introduction. Systems and Computer Engineering . Carleton University, Ottawa. 11.

5. Roy, B. V. Mason, K.(2005). Formulation and Analysis of Linear Programs, Chapter 5 Network Flows .

6. Vanderbei, R. J. (2020). Linear programming: foundations and extensions (Vol. 285) . Springer Nature.

7. Sobel, J. (2014). Linear Programming Notes VIII: The Transportation Problem .

8. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Section 26.2: The Ford–Fulkerson method". Introduction to Algorithms (Second ed.). MIT Press and McGraw–Hill.

9. Jon Kleinberg; Éva Tardos (2006). "Chapter 7: Network Flow". Algorithm Design. Pearson Education.

10. Ford–Fulkerson algorithm . Retrieved December 05, 2020.

11. Hu, G. (2020, November 19). Simplex algorithm . Retrieved November 22, 2020.

12. Altınel, İ. K., Aras, N., Şuvak, Z., & Taşkın, Z. C. (2019). Minimum cost noncrossing flow problem on layered networks . Discrete Applied Mathematics, 261, 2-21.

13. Dewil, R., Vansteenwegen, P., Cattrysse, D., & Van Oudheusden, D. (2015). A minimum cost network flow model for the maximum covering and patrol routing problem . European Journal of Operational Research, 247(1), 27-36.

14. Lin, D. Y., & Chang, Y. T. (2018). Ship routing and freight assignment problem for liner shipping: Application to the Northern Sea Route planning problem . Transportation Research Part E: Logistics and Transportation Review, 110, 47-70.

15. Tu, Q., Cheng, L., Yuan, T., Cheng, Y., & Li, M. (2020). The Constrained Reliable Shortest Path Problem for Electric Vehicles in the Urban Transportation Network . Journal of Cleaner Production, 121130.

16. Guo, Y., Li, S., Jiang, W., Zhang, B., & Ma, Y. (2017). Learning automata-based algorithms for solving the stochastic shortest path routing problems in 5G wireless communication . Physical Communication, 25, 376-385.

17. Haddou, N. B., Ez-Zahraouy, H., & Rachadi, A. (2016). Implantation of the global dynamic routing scheme in scale-free networks under the shortest path strategy . Physics Letters A, 380(33), 2513-2517.

Optimization of Computer Networks by Pablo Pavón Mariño

Get full access to Optimization of Computer Networks and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

Chapter 5 Capacity Assignment Problems

5.1 introduction.

$c5-math-0001$

(Slow) Capacity planning : In Internet Service Provider (ISP) backbone networks, network links are virtual circuits hired to a network carrier,or transport connections established in an own network infrastructure. The link costs depend on the link distance and capacity according to the carrier tariffs or the infrastructure cost structure. ISPs periodically (e.g., every 6 months) execute a so-called capacity planning process [1] or capacity expansion ...

Get Optimization of Computer Networks now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Services on Demand

Related links, south african computer journal, on-line version issn 2313-7835 print version issn 1015-7999, sacj vol.29 n.1 grahamstown jul. 2017, http://dx.doi.org/10.18489/sacj.v29i1.393 .

RESEARCH ARTICLE

Optimising capacity assignment in multiservice MPLS networks

Abdoul Rassaki I ; Andre Nel II

I Applied Information Systems, University of Johannesburg. [email protected] II School of Mechanical and Industrial Engineering, University of Johannesburg. [email protected]

The general Multiprotocol Label Switch (MPLS) topology optimisation problem is complex and concerns the optimum selection of links, the assignment of capacities to these links and the routing requirements on these links. Ideally, all these are jointly optimised, leading to a minimum cost network which continually meets given objectives on network delay and throughput. In practice, these problems are often dealt with separately and a solution iterated. In this paper, we propose an algorithm that computes the shortest routes, assigns optimal flows to these routes and simultaneously determines optimal link capacities. We take into account the dynamic adaptation of optimal link capacities by considering the same Quality of Service (QoS) measure used in the flow assignment problem in combination with a blocking model for describing call admission controls (CAC) in multiservice broadband telecommunication networks. The main goal is to achieve statistical multiplexing advantages with multiple traffic and QoS classes of connections that share a common trunk present. We offer a mathematical programming model of the problem and proficient solutions which are founded on a Lagrangean relaxation of the problem. Experimental findings on 2-class and 6-class models are reported.

Keywords : MPLS, network capacity assignment, optimal routing, link flow, Lagrangean relaxation, QoS.

1 INTRODUCTION

The operation, performance and system cost of today's telecommunication networks are challenged by the routing, flow and capacity assignment strategy. MPLS networks are not immune from these challenges. Of primary importance in the design of the MPLS network is to ascertain the optimal link capacities and routes to be used between each origin-destination (O-D) pair, thereby mitigating system cost. The preferred outcome in network design is to minimize overall system costs which are composed of a) connection costs depending on capacities and end-to-end delay, and b) transfer costs which are incurred due to the limited line and node capacities. A profitable design will make simultaneous decisions on both routing and link capacities as they are closely related. Determining the routing between origin-destination pairs and assigning capacities to the links used by those routes is known as the capacity and flow assignment (CFA) problem (Gavish & Altinkemer, 2000).

In the MPLS network design process, tradeoffs have to be made between the response time for clients and the costs of the network. If high capacities are assigned to the network links, then we see elevated connection costs but a low response time. Conversely, if low capacity links are installed, the reverse will be true. This argument shows that the tradeoffs between response time and connection costs are an integral part of the proper design and operation of a communication network. The main focus of this research is on issues concerning routing and capacity assignment particularly in MPLS networks and more generally in all routed telecommunication networks. Currently, network designers use heuristic solution techniques during the design process. However, it is not possible using only such techniques to analyze the quality of the resulting design in terms of cost and response time.

Innovative techniques for MPLS network optimisation, subject to constraints on routing effected by QoS and other parameters, were recently established and illustrated in Rassaki and Nel (2013). The outcome of the investigation was to substantiate how to capitalize on the available bandwidth and diminish the results of network overcrowding with MPLS Traffic Engineering (TE).

An MPLS network is comprised of a pair of nodes known as label switching routers (LSRs). These LSRs have the capacity to switch and route packets using information stored in the label attached to each packet. To begin the process, a label switched path (LSP) is established for the packets being routed and distributed, and QoS considerations are determined for the LSR The parameters for QoS consist of the queuing and discarding protocols for every LSP on the path as well as the resources that are required to sustain the path. The establishment of the LSP and of the QoS parameters leads to the creation of the forwarding equivalence class (FEC). The FEC denotes a grouping of packets sharing transportation requirements. All packets in an FEC receive the same treatment on the way to the destination. These packets follow the same path and receive the same QoS treatment at each hop. The LSRs simply advance every packet on the strength of its own label value as it is unnecessary to scrutinize or analyze the packet's IP header. Each LSR builds a table, known as label information base (LIB), to specify how a packet must be treated and forwarded. The outcome of this process is that the forwarding mechanism used by an LSR is more straightforward and more timely than that of an IP router.

Packets arrive at an MPLS switching domain via an ingress LSR found at the border of the MPLS network. The ingress LSR reviews the packet to establish the required QoS, then allocates the packet to an FEC and LSP Next, it attaches the relevant label to the packet which is then directed to the next LSR down the LSR Within the MPLS network, every LSR on the length of the LSP collects the previously labeled packet and then transmits it to the subsequent LSR along the LSP. As the packet is received by the egress LSR at the periphery of the network closest to its destination, the edge LSR removes the packet's label, reviews the IP packet header and then directs the packet to its ultimate destination.

Multiprotocol label switching (Rosen, Viswanathan, & Callan, 2001) has many valuable attributes for Internet traffic engineering (TE), and as such will be extensively utilised for TE (Awduche, Malcolm, Agogbua, & McManus, 1999). In a straightforward manner, MPLS can establish an explicit-route label switched path (ER-LSP) as necessary, through manual administrative action or traffic requirement by applying CR-LDP (Jamoussi, 2002) or RSVP-TE (Awduche et al., 2001) signaling protocols. Further, traffic trunks that are comprised of traffic flows with comparable traits or traffic needs can simply be mapped on that ER-LSP

One of the primary motivations behind our research is the emergence of TE support in IP networks, for example in networks found to be using the MPLS protocol. The requirement of choosing the topology and scope of MPLS "explicit routes" to convey QoS multiservice is also discussed here. MPLS facilitates multiple paths from origin to destination since this protocol imparts the promise of advantageous network wide load balancing, which is a benefit that corresponds nicely with our current work. Further, it has been noted that it is equally beneficial to merge differentiated services (DiffServ) and MPLS protocols by applying QoS multiservice traffic on explicit routes (Wu, Cheval, & Vaananen, 1998).

From a "fast forwarding" technology, MPLS has evolved into a set of protocols that offers sophisticated traffic engineering options, Virtual Private Networks (VPNs) and multi-protocol support through logical distinction between IP forwarding and routing. MPLS has been widely deployed on the ISP backbone to replace Asynchronous Transfer Mode (ATM) and traditional IP routing. Further, it has been introduced into metro and access-networks, and even some private enterprise networks (Stallings & Case, 2013).

This paper develops mathematical programming techniques that directly consider both costs as well as service quality to design and operate telecommunication networks. A major incentive is the vigorous revision of link capacities by considering the same criterion used in the flow assignment problem in combination with a blocking model for describing call admission controls in multiservice broadband networks. Traffic of a number of different types requiring different bandwidth allocations is offered to each source-destination pair. The network manager must implement a call admission control scheme to minimize the packet delay and maximize the throughput earned from the network while maintaining agreed QoS constraints.

Section 2 presents a study of literature of closely related work, and the critical review thereof. In Section 3, we first describe our modeling framework then a nonlinear integer programming formulation of the network design problem is given. The following Sections 4 and 5 present our optimal capacity assignment formulation and algorithm. Section 6 presents the analytical evaluation of the network model. We introduce our multiservice blocking and network models in Sections 7 and 8. The basis of comparing two different call admission control parameters and performance are discussed in Section 9. Lastly, the conclusions are presented in Section 10.

2 REVIEW OF RELATED WORK

The topological design of distributed computer networks in capacity assignment is a subject with comparatively few published results, given that it has been studied since the late 1970s (Gerla, 1975; Maruyama & Tang, 1976; Kleinrock, 1976). As such, this complex field continues to be challenging to study; however, there are some recent findings on relative bandwidth allocation techniques (Martens & Skutella, 2006; Pompili, Scoglio, & Shoniregun, 2007; Truffot, Duhamel, & Mahey, 2010; Rassaki &Nel, 2015).

Most of the available literature examining this problem handles capacity assignment and flow assignment separately. All these research approaches to capacity assignment, also utilize different performance criteria. In the capacity assignment problem (Gerla, 1975; Maruyama & Tang, 1976; Amiri, 1992) the routing protocol is understood to be given and the optimal capacity for every link is chosen from within a discrete set of line capacities. The flow assignment problem (Bertsekas & Gallager, 1992; Kershenbaum, 1993; Kleinrock, 1976) begins with a given assignment of link capacities, critical paths between O-D pairs are established to minimize either the average message delay or the maximum message delay in the network.

An additional approach is to improve an existing network by redistributing the link capacities while maintaining the total sum of all capacities of the network.

It is important to note the distinction between the uncapacitated MPLS design problem where the capacities (bandwidth) of the physical links are the decision variables, and the capacitated MPLS design problem where the capacities of the physical links appear as constraints. The uncapacitated problem has been studied by, among others, Rohne, Jensen, Svinnset, and Venturin (1998), who first design a physical network under the assumption that all traffic will be routed on a node-by-node basis, and then configure the LSP highways by cross connecting flows in the physical network according to a cost model. Bauschert (1997) also considers the uncapacitated problem and uses a set of iteration loops to simultaneously design a virtual path connection network (VPCN) and virtual connection (VC) routing policy. This scheme relies on an initial pre-selection of paths and includes linear programming models.

A distinction is also made between real valued MPLS configurations and integer valued configurations. In the former, bandwidth is regarded as a resource which can be shared in any fashion while in the latter only certain sharing schemes are possible.

The most conventional manner of resolving the capacitated MPLS design problem is to draw on constrained non-linear programming (NLP) techniques. Unfortunately, with a network of any size, issues such as the quantity of decision variables and computation times grow to such a degree that these techniques become unrealistic to implement. Herzberg and Byes (1993) linearize the problem with a goal of reducing the computational burden while also arriving at integer valued solutions using standard LP solvers, but do not touch upon the problem of a large state space.

Balakrishnan and Graves (1989) study the special case of piecewise linear costs in directed networks, where each link is assigned a capacity and a path is identified for each O-D pair. In this study, the problem of the routing and capacity assignment is devised as a mixed integer program and a composite algorithm is developed to generate both lower bounds and feasible solutions. The model however does not take into account the delay issue that arises when link capacity utilisation reaches certain levels. LeBlanc and Simmons (1989) articulate the routing and capacity assignment problem with continuous link capacity variables. In addition, they propose an innovative convex delay function, demonstrating that, for their assumed length distribution, this novel function forecasts delay with more accuracy than the conventional delay function when flow-capacity ratios are less than 0.80. Computation results have been conveyed for networks with as many as 100 nodes.

Gopal, Kim, and Weinrib (1991) and Arvidsson (1995) devise heuristic optimisation algorithms that maximize a function in a sequence of steps which converge to a local optimum. These algorithms belong to the category of purported greedy algorithms which sees the steps taken at each optimisation point are those immediately giving the utmost reward with no consideration for long term repercussions. Whereas Gopal et al. rely on predefined paths, Arvidsson includes path searching in his algorithm. Pióro and Medhi (2004) surveyed and evaluated a large number of problems related to optimisation techniques. The reader can refer to Pióro and Medhi (2004) for a comprehensive list of references relating to network optimisation from a mathematical viewpoint.

Maruyama, Fratta, and Tang (1977) incorporate heuristic methods for capacity assignment (developed in Maruyama & Tang, 1976) into a more general procedure that iterates between a composite capacity assignment algorithm and flow assignment phase until a local optimum is reached. They also describe a priority assignment scheme which, with high likelihood, yields a less costly capacity assignment satisfying the delay requirements. A similar iterative procedure which alternates between capacity and flow assignment is used by Fratta, Gerla, and Kleinrock (1973) where different heuristic methods based on the flow deviation algorithm (Maruyama et al., 1977) for static route assignment is presented.

Gershet and Weihmayer (1990) examine the issue of assigning capacities to network switches and potential links in order to accommodate traffic demand between nodes and satisfy a performance requirement that specifies an upper bound on the link utilisation. The goal is to minimize switch and link capacity costs which are assumed to be continuous. A solution procedure which alternates between solving an uncapacitated design/routing subproblem and a capacity assignment subproblem is presented. The procedure is applied to a real network with 20 nodes and two levels of link capacities.

Gavish and Altinkemer (2000) expand upon the research of Whitney (1972) by taking into account every potential route for each communicating node pair. They devise the problem, using Lagrangean relaxation inserted in a subgradient optimisation methodology in order to realize lower bounds and a practicable resolution to the problem. They incorporate cut constraints which are redundant in the initial problem to better the lower bounds. These cut constraints are understood to have been classified in advance of the start of the solution procedure. Clearly the value of the solution relies a great deal on the number and selection of the cuts.

As can be seen from the short summary of the literature, the capacity and flow assignment problem is typically separated into two subproblems: capacity assignment, and route determination. These two issues are correlated, as the capacity designated to a link and the delay sustained by a particular flow utilising that link are connected. As such, examining these problems independently of one another may result in unsatisfactory outcomes. Having the routing method remain unchanged and attempting to make the best use of the capacity assignment, or vice versa, does not get to the core of the characteristics integral to the problem and could therefore produce sub-optimal results.

A further shortcoming of the earlier research perspectives is the absence of theoretical or empirical methodology to assess the value of the proposed solutions.

3 MODELING AND ANALYSIS

In this section, we present the appropriate notation and definitions and follow this with the collection of assumptions that define our model of the network. We identify the class of analysis and synthesis problems that confront us in network studies.

Our interest is in the numerical resolution of the ensuing network flow problem, subject to a constraint that the total link capacity not exceed C i j :

Minimize: The average end to end network delay.

We further believe that the cost of building the channel with capacity C ij is given by d ij C ij , an arbitrary function of the capacity and of the channel. If we say that D signifies the cost of the whole network, which we understand to be comprised of only the cost 1 of channel construction, we then have

where d ¡j is the positive cost per unit capacity on link (i, j).

We have earlier defined message delay as the total time it takes for a message to travel across a network. What we are more interested in, though, is the average message delay (2) and we consider this to be our key performance indicator.

In any practical network design procedure, a large number of design variables suggest themselves. Among these we include: the selection of channel capacities; the form of routing procedure; the form of flow control procedure; the topological design of the network; the storage capacity at each node; the choice of hardware and software programs to be used for the switching computer; the partitioning of messages into various-size packets; and so on. Since we are interested mainly in the queueing problems in this paper, we discuss neither the hardware nor many aspects of the software design of the switching computer itself any further.

4 PROBLEM FORMULATION

This section begins by considering the problem of assigning optimal capacities to the links in the network given the link topology (location of the nodes and links) and link flows. We consider a network consisting of N nodes and L links. The links have original capacities C 1 , C 2 , . . . , C L measured in bits/sec. Let i - j denote the link connecting O-D pair (i, j). Link i - j has capacity Qj measured in bits/sec. There are S classes of messages.The traffic requirements between the node pairs are measured in bits per second. We assume a flow distribution - a flow on each link which satisfies the requirements.

The objective is to compute the optimal link capacities for a network where the topology and traffic flows are known and fixed which minimizes the average network delay subject to the linear overall cost of the system:

In essence, we want to establish both the scope of resource capacity required for the given demand volume, and the manner in which to reasonably and efficiently disseminate it through the network using a series of routing/flow constraints. This determination, which is typically found in medium to long-term network planning, is broadly known as uncapacitated design.

When the network capacity is established and the demand volume is understood, the question becomes how to assign flows on distinct paths in such a way that specified network objectives (e.g., minimum cost routing or maximum total revenue) are optimised. The system costs are composed of connection costs which depend on link capacities and delay costs incurred by users due to the limited capacities of the links and the resulting queueing at intermediate nodes.

We wish to focus on three very basic design parameters that we must consider: first is the selection of the channel capacities Qj; second is the selection of the channel flows ; and third there is the topology itself. All of these may be varied to improve network performance. The notion of "optimum design" is extremely difficult to achieve in any realistic network design; however we define, the performance criterion, which is the average message delay T , and attempt to minimize this quantity (thereby optimising performance). This approach will allow us to make some important qualitative statements about network design and performance. Of course, any optimisation problem must be subject to some form of cost constraint, and here we choose the fixed cost constraint given in Eq. (4). Therefore we have a performance measure T , a cost constraint D, and three variables design "parameters," C tj , F tj , and the topology.

This study overcomes serious shortcoming of previous methods suggested in past research. In the routing selection process, these methods assume that a set of pre-specified candidate routes chosen from among all possible routes is given for every communicating O-D pair. Evidently, the value of the solutions offered by these methods relies greatly on the selection of the candidate route sets determined before the procedure is employed. The use of only a subset of all possible routes by these methods results in a practical limitation which is the potential of producing lower bounds higher than the values of the optimal solutions to the routing and capacity assignment problem. Our solution method removes this shortcoming by considering every promising route for each communicating node pair.

What is particularly attractive about the method known as Lagrangean relaxation is the way it offers both upper and lower bounds on the value of the objective function (Berezner & Krzesinski, 2001). In other words, it is understood that the optimal objective function value rests between the value of the best feasible solution found and a value that it can be no better than. In this paper, a Lagrangean problem is established by multiplying some of the constraints by Lagrange multipliers and adding them to the objective function. As a result, the Lagrangean problem is divisible to a routing subproblem and a link subproblem. Every category of subproblem is further divisible into subproblems for every link and for every communicating pair. The link subproblem consists of assigning a capacity to a link and the route subproblem deals with choosing a route for a communicating O-D pair.

To minimize the objective function, we proceed by using a Lagrange multiplier β and by forming the Lagrangean relaxation function as follows:

where D is the total cost of the network and T is given by the M/M/1 delay function:

In Eq. (6), if we find the minimum value of L with respect to the capacity assignment, then we will have found the solution to the capacity assignment problem since the bracketed term is identically equal to zero. The parameter β is the undetermined multiplier to be evaluated.

If β is large enough, it is a penalty for violating the constraint on total capacity. If the sum of the exceeds D, the term in the brackets is positive and if multiplied by β increases the value of the objective to be minimised. Values of C tj are sought which do not violate the constraint. If β is too large, however, it is possible to make this new objective function smaller by letting the sum of the C tj become strictly less than D, thus minimising the new objective function but not the original one. As β increases from zero, the sum of the C tj decreases as the first term is traded in the objective against the second. There is a unique value of β which makes the sum exactly equal to D. This is the value sought along with the corresponding values of the C tj .

Solving for C lj gives:

The objective now is to find the value of β . Once we have evaluated the constant β , this will be our solution.

From this equation, solving for β gives,

Using this last form in the Eq. (9), the optimal solution to the capacity assignment problem is

The solution to the Lagrangean problem for any specific values of the Langrange multipliers often breaches one or more of the relaxed constraints. Several Lagrangean-based algorithms include additional heuristics which allow these infeasible solutions to become feasible. As such, the algorithms can provide welcome solutions to the initial framework. The top feasible solutions of those offered by the procedure at any point denote the upper bound on the value of the true optimal solution.

The disparity that is seen between the upper and the lower bounds is known as the gap. Should the value of the gap become zero (or some minimum value determined using the integer properties of the model), we will have arrived at the optimal solution. If not, but the gap becomes satisfactorily small (e.g. less than 1%), the analyst might halt the procedure, content that the current best solution is within 1% of optimality.

In implementing Lagrangean relaxation, we are challenged to select which constraints will be relaxed. The objective is to have a relaxed problem which can be easily resolved and bring about ideal lower bounds. As the relaxed model may require solving hundreds or thousands of times while seeking the best multiplier values, the simplicity of the solution is vital to achieving the desired outcomes. Preferably, the solution to the relaxed problem will found by inspection or simply by sorting the objective function coefficients.

The algorithm assumes:

1. The nodes of the network and the input traffic flow for each pair of nodes are known. 2. A routing model determines the optimal flows F tj of all links (i, j) given the link original capacities Cj . We assume that the link flows minimize a cost function and F tj can be determined by minimising the average packet delay,

based on the M/M/1 channel model, where γ is the total input traffic into the network, and Cj and p[ are the capacity and the processing and propagation delay, respectively, of link (i, j). The algorithms described in Rassaki and Nel (2013) can be used for this purpose.

4.1 The algorithm

This section describes the different steps of the capacity assignment algorithm and how it works. The steps of the capacity assignment algorithm

Step 1: Select a network topology with initial capacities and requirements.

Step 2: Compute optimal link flows that minimize the average delay for the network using the FOA algorithm.

Step 3: Allocate the link capacities to minimize the delay with the link flows computed in step 2, given the constraints on the total cost of a system.

Step 4: Use these link capacities instead of the original capacities with the original requirements and go to step 2. The delay calculated in this step will be less than in step 2.

Step 5: Reallocate the optimal link capacities with the optimal link flows from step 4. The new delay will be smaller than the delay in step 3.

There is a guarantee of the convergence of the algorithm due to the finite (albeit large) number of shortest route flows. Because of the decrease in delay, repetitions of the same flow do not exist. And since the delay decreases with every iteration and it is positive, the algorithm converges.

5 NETWORK PERFORMANCE ANALYSIS

An application of our algorithm to the network topology shown in Figure 1 is next introduced. The network model consists of 8-nodes and 10-links which is a fictitious network connecting eight South African cities in different provinces to compute the optimal link capacities. Each link carries traffic in both directions. The double lines between nodes 3 and 4 and 7 and 8 indicate that there are two links in each direction connecting these nodes. The network carries 2 traffic classes: the bandwidth requirement of the first class is 1 unit and the bandwidth requirement of the second class is 40 units.

The capacity of each link is 5624 units. The traffic intensity matrix is given in Table 1 . Note that the table has zeros on the main diagonal and infinity (denoted by'-' here) wherever no links exists. Note also, that the mapping of the distance between cities is being done randomly and does not necessarily reflect the physical distance between cities. The class dependent intensities are given by p s j = γ s b s where p i j represents the traffic intensity between link (i, j) , γ ί ; is the class load factor and b s the bandwidth. These values are given in Table 2 .

Our algorithm and its variants adapted to the problems have been coded in C++ and compiled through gcc - on the GNU/Linux system. The numerical tests were performed on an Intel Core i3-2310 [email protected] computer with 2.5Gb RAM.

We now compare the network optimal link capacities with their initial values. The experiment results are expressed by presenting the values of the optimal routes, the optimal flow solution, the optimal link capacities and the average end to end delay in the network corresponding to the best feasible solution. An outcome of these experiments was that we were able to verify ways to optimize available bandwidth usage and also minimize the impact of traffic congestion on the network using MPLS TE.

Table 3 shows the optimal link flows and capacities computed after the convergence of the capacity assignment algorithm. The optimal and initial link capacities' values calculated are displayed in Figure 2 .

Figure 3(a) plots the capacity assigment for link (1-2) as the algorithm executes while the network delay is plotted in Figure 3(b) as the algorithm executes. The delays converge after 44 iterations. That is, when the newly calculated network delay is not significantly better than the previous one. One can see the convergence of the algorithm and how the network delay gets better and better after each iteration in Figure 3(b) . These results are obtained through explicit routing, in that an explicit LSP is already established through the network, profiting from all available network resources. Further, we were able to offer a degree of resource assurance with MPLS QoS elements. In particular, we were able to verify how to best plot traffic into a specific LSP with the aim of IP network performance enhancement.

Comparison with Figure 3(a) shows a strong correlation between the delay and the assigned capacity. This can be expected since the delay is a function of capacity. The delays decrease since the flows are shifted onto optimal paths in order to reduce the delays on congested links. The smaller flow on the congested links in turn leads to a decrease in the capacity required to achieve a given delay.

There are several approaches to capacity assignment, utilising different performance criteria. An additional approach is to improve an existing network by redistributing the link capacities while maintaining the total sum of all capacities of the network.

Kleinrock (1976) notes that the selection of an appropriate algorithm to allocate capacities will depend on the cost-capacity structure, on the presence of additional topological constraints, on the degree of human interaction allowed and, finally, on the tradeoff between cost and precision required by the particular application. Kershenbaum (1993) describes a capacity assignment approach that guarantees an optimal solution but can take an inordinate amount of time. The algorithm can yield some approximate results by alternatively strengthening the dominance criterion. Another approach originally proposed by Whitney guarantees a solution in a reasonable amount of time and also gives a bound on the quality of the solution it obtains (which is not, in general, optimal).

6 MULTISERVICE BLOCKING MODEL

In this section, we again model a network as a grouping of available means that allows telephone calls to arrive randomly. These telephone calls all have a related holding time and class. However, this time a call can be blocked.

The FOA (Rassaki & Nel, 2013) uses an objective function based on the M/M/1 queue. In this system, if a message or customer arrives when the channel is not busy, (i.e., no message in transmission), the message is transmitted immediately. If the channel is busy when the message arrives, the message is placed in a queue where it waits until the channel becomes free and then begins serving the next message.

Not all the systems deal with congestion by allowing messages to wait. Most traditional telephone systems block calls from entering the system if no capacity is available. Ross (2012) defines a loss system as a set of accessible means to which calls, each with a linked holding time and class, arrive at random instances.

This kind of system is fundamentally different from a queueing system because a call's system time is equal to its holding time. Here, a call arrives and requires a fixed amount of capacity, enough to handle a conversation. If the capacity is available, it is dedicated to the call for its duration. If not the call is blocked and lost. We consider such a system in this section.

6.1 Network model

Our goal is to obtain a capacity assignment such that the link blocking probabilities satisfy a certain grade of service (GoS).

6.2 Implementation

6.3 Blocking probabilities

There are several options for the blocking function E t (.) (Ross, 2012; Ross, Tang, & Wang, 1994) and references therein for examples). The authors introduce the stochastic knapsack to which objects arrive and depart at random times. We have opted to use the stochastic knapsack algorithm which, along with the computation of multiservice blocking probability, is described in Berezner and Krzesinski (2001).

The implementation starts by computing link flows that are optimal in terms of the network delay. Then we compute the link blocking probabilities using these flows for each link. To calculate the probabilities we need the traffic intensities for different classes which are given by p s . = p u Y s b s where p i j represents the traffic intensity on link (i, j ), y s is the class load factor and b s the bandwidth. After calculating these intensities, we run the multiservice blocking probability algorithm. The algorithm uses the link capacity as a loop index. Thus we first calculate blocking probabilities for the link with capacity 1, then use this to calculate for link with capacity 2, and so on. Each step reduces probabilities and it is quite natural: we expect calls to be lost less frequently on links with higher capacities. When the capacities are large enough, the blocking probability tends to zero. The iteration terminates as soon as the average blocking probability becomes less than the GoS required.

6.4 Service Separation

In this case, we calculate the optimal link capacities required for every class with certain blocking probability, then we sum all capacities to obtain the capacity on a link. Consider again the network model in Section 6. The network consists of 8 nodes and carries 2 traffic classes. The traffic intensity matrix is given in Table 1 and the class dependent intensities are given by multiplying these values by the load factors.

Table 4 summarizes the results of the computational tests. It presents the link blocking probabilities per service class for service integration as well as service separation and we compare the link capacities produced by the two services in Table 5 .

We can see from both Table 5 and Figure 4 that links with larger flows have larger capacities and therefore smaller service times which is a factor contributing to the reduction in the total delay of the network. The network model described in the previous section was capacitated with a GoS of 1%.

Ross (2012) and others have written papers on the issue of determining grade of service allocation to multi services connections (Chlebus, Coyle, Henderson, Pearce, & Taylor, 1994; Bean, Gibbens, & Zachary, 1995).

Note that our experiment combines two different models: the blocking model and the queueing model. However, these models are applied at different stages. First we have the queueing model associated with a network delay. Secondly, we have the blocking model associated with calls blocked and packets dropped. In first case, the capacities must be enough to accomodate the optimal flows, otherwise the network delay becomes indefinite. In the second situation, some capacities might be insufficient and calls will be dropped.

In order to evaluate the effect of applying service separation, we also compute the optimal link capacities for service integration and then compare the two. The total link capacity computed in service separation is the sum of the capacities required in both traffic classes.

Our conclusion is that the new capacity is sometimes larger than in the case of complete sharing; this is the penalty for service separation; the penalty is however not too large. For example, for link (4,5) the link capacity on complete sharing is 4645 while the separation case is 4647.

7 CONCLUSIONS AND FUTURE WORK

The thrust of this work is twofold: a) to select the optimal routes and link capacities for MPLS networks and b) to conduct the analysis at the call level in the presence of multiservice traffic sources. Overall system costs are minimised by trading off link capacity costs versus expected network delay costs.

The model is developed for MPLS networks managers and users who deal with these tradeoffs. It is an extension of the method described in Rassaki and Nel (2015) that is applied to thousands of IP networks. The new approach combines two different models: the queueing model and the blocking probability model. First, we have the queueing model associated with the expected network delay. Secondly, we have the blocking model associated with calls blocked and packets dropped. In first case, the capacities must be enough to accommodate the optimal flows, otherwise the network delay becomes indefinite. In the second situation, some capacities might be insufficient and calls will be dropped.

Considering the most basic model, we see one individual transmission link accepting input traffic that results from the superposition of N traffic classes. Two CAC strategies are defined for the multiservice structure in which a distinct level of service is necessary for every class. The comparison between the two strategies brings the following conclusions: a) service separation is not the most appealing option for two reasons: weak performance, and a higher degree of resource management complexity and service deployment; b) the test results for service integration reveal concerns about fairness in some circumstances, even though it is less difficult to put into practice; and c) test outcomes are somewhat influenced by the holding time distribution (specifically, blocking probabilities are dependent on the offered traffic, but also on the arrival rate and holding times).

Selecting an acceptance threshold is significant as far as implementation in a realistic network environment. It is essential to be aware of, in advance, every potential traffic class and to establish a GoS administrative protocol for these classes. Although there will be supplementary complexity costs, the bonus of expanded capacity makes them defensible.

In future work, we plan to improve and assess unique effective procedures to deliver QoS differentiation to the IP flows passing through the MPLS domain.

Amiri, A. (1992). Routing and capacity assignment in backbone communication networks (Doctoral dissertation, Ohio State University). [ Links ]

Arvidsson, Ä. (1995). High level B-ISDN/ATM traffic management in real time. In Performance modelling and evaluation of ATM networks (pp. 177-207). Springer. https://doi.org/10.1007/978-0-387-34881-0_10

Awduche, D., Berger, L., Gan, D., Li, T., Srinivasan, V, & Swallow, G. (2001, December). IETF RFC 3 209: RSVP-TE extension to RSVP for LSP tunnels. Internet Engineering Task Force.

Awduche, D., Malcolm, J., Agogbua, J., & McManus, J. (1999, September). RFC 2702: Requirements f or traffic engineering over MPLS. Internet Engineering Task Force.

Bauschert, T. (1997). Multihour design of multi-hop virtual path based wide-area ATM networks. P roceedings of 15th International Teletraffic Conference, 1019-1030.

Bertsekas, D. & Gallager, R. (1992). Data networks (2nd). Prentice-Hall, Englewood Cliffs. [ Links ]

Chlebus, E., Coyle, A., Henderson, W., Pearce, C. E. M., & Taylor, P G. (1994). Mean-value analysis for examining call admission thresholds in multiservice networks. In The Fourteenth International T eletraffic Conference, Antibes, France.

Fisher, M. L. (1981). The Lagrangian relaxation method for solving integer programming problems. M anagement science, 27(1), 1-18. [ Links ]

Gavish, B. & Altinkemer, K. (2000, December). Backbone network design tools with economic tradeoffs. ORSA Journal of Computing, 2, 226-252. [ Links ]

Gerla, M. (1975). Approximations and bounds for the topological design of distributed computer network. In ACM 4th Int Confon Data Communications Symposium, Quebec, Canada.

Gershet, H. & Weihmayer, R. (1990). Joint optimization of data network design and facility location. IEEE Journal on Selected Areas in Communications, 8, 149-152. [ Links ]

Gopal, G., Kim, C.-K., & Weinrib, A. (1991). Algorithms for reconfigurable networks. In 13th International Teletraffic Congress Proceedings (pp. 288-289). Citeseer.

Herzberg, M. & Byes, S. (1993). Bandwidth management for reconfigurable multi-service networks. Australian Teletraffic Research, 25(2). [ Links ]

Jamoussi, B. e. a. (2002, January). IETF RFC 3212: Constraint-based LSP setup using LDP. Internet Engineering Task Force.

Kershenbaum, A. (1993). Telecommunications network design algorithms. McGraw-Hill.

Kleinrock, L. (1976). Queueing systems vol 2: Computer applications. John Wiley and Sons.

Maruyama, K. & Tang, D. T. (1976). Discrete link capacity assignment in communication networks. In ICCC 3rd Int Conf, Toronto, Canada (pp. 92-97).

Pióro, M. & Medhi, D. (2004). Routing, flow, and capacity design in communication and computer networks. Elsevier.

Rassaki, A. & Nel, A. (2013, August). Quality of service in MPLS networks. In IASTED 15th Int C onference on Control and Applications, Honolulu, USA, pp 67-74, Aug. 2013.

Rassaki, A. & Nel, A. (2015). Optimal capacity assignment in IP networks. In Digital Information Processing and Communications (ICDIPC), 2015 Fifth International Conference on (pp. 256-261). IEEE. https://doi.org/10.1109/icdipc.2015.7323038

Rohne, M., Jensen, T., Svinnset, L., & Venturin, R. (1998). Designing VP networks. In Fourteenth N ordic Teletraffic Seminar, Copenhagen, Danemark (pp. 17-30).

Rosen, E., Viswanathan, A., & Callan, R. (2001, January). IETF RFC 3031: Multiprotocol label switching a rchitecture. Internet Engineering Task Force.

Ross, K. W. (2012). Multiservice loss models for broadband telecommunication networks. Springer Science & Business Media.

Stallings, W. & Case, T. (2013). Business data communications infrastructure, networking and security. Upper Saddle River, NJ. Pearson, Education Inc. [ Links ]

Whitney, V (1972). Lagrangian optimization of stochastic communication systems models. In Proceedings MRI Symposium on Computer-Communication Networks, Brooklyn, New York (pp. 332-342).

Wu, L., Cheval, P, & Vaananen, P (1998). MPLS extensions for differential services. Internet Engineering Task Force. Retrieved from https://tools.ietf.org/html/draft-wu-mpls-diff-ext-00

Received: 9 June 2016 Accepted: 23 February 2017 Available online: 9 July 2017

1 The cost of the nodes may be incorporated in the channel cost directly.

Network capacity assignment for multicast services using genetic algorithms

Ieee account.

Change Username/Password
Update Address

Purchase Details

Payment Options
Order History
View Purchased Documents

Profile Information

Communications Preferences
Profession and Education
Technical Interests
US & Canada: +1 800 678 4333
Worldwide: +1 732 981 0060
Contact & Support
About IEEE Xplore
Accessibility
Terms of Use
Nondiscrimination Policy
Privacy & Opting Out of Cookies

A not-for-profit organization, IEEE is the world's largest technical professional organization dedicated to advancing technology for the benefit of humanity. © Copyright 2024 IEEE - All rights reserved. Use of this web site signifies your agreement to the terms and conditions.

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

We're Hiring!
Help Center

A Genetic Algorithm to Solve Capacity Assignment Problem in a Flow Network

Computer networks and power transmission networks are treated as capacitated flow networks. A capacitated flow network may partially fail due to maintenance. Therefore, the capacity of each edge should be optimally assigned to face critical situations-i.e., to keep the network functioning normally in the case of failure at one or more edges. The robust design problem (RDP) in a capacitated flow network is to search for the minimum capacity assignment of each edge such that the network still survived even under the edge's failure. The RDP is known as NP-hard. Thus, capacity assignment problem subject to system reliability and total capacity constraints is studied in this paper. The problem is formulated mathematically, and a genetic algorithm is proposed to determine the optimal solution. The optimal solution found by the proposed algorithm is characterized by maximum reliability and minimum total capacity. Some numerical examples are presented to illustrate the efficiency of the proposed approach.

Related Papers

Moatamad Mohamed

The robust design in a flow network is one of the most important problems. It is defined as searching the optimal capacity that can be assigned to the nodes such that the network still survived even under the node's failure. This problem is considered NP-hard. So, this study presents a genetic-based algorithm to determine the maximum node capacity for a two-commodity flow network with node failure. I.e., searching the minimum sum of the assigned capacities and the maximum network reliability. The obtained results show that The proposed GA-based algorithm succeeded to solve the robust problem for the two-commodity flow network considering the node's failure.

Younes Hassan

Abdelhamid Daamouche

System reliability is an important performance index for many real-life systems, such logistic information system, electric power systems, computer systems and transportation systems. These systems can be modelled as stochastic-flow networks (SFNs) composed of arcs and nodes. In this paper, we investigate components assignment problem for stochastic flow networks subject to two constraints namely total lead-time, and system reliability. A new approach based on random weighted genetic algorithm (RWGA) is proposed for searching an optimal components assignment which leads to maximizing system reliability and minimizing total lead time. The results revealed that an optimal components assignment leads to the maximum reliability and minimum total lead-time using the proposed approach. Keyword Component Assignment Problem, Genetic Algorithm, Lead-Time, System Reliability.

Many real-world networks such as freight, power and long distance transportation networks are represented as multi-source multi-sink stochastic flow network. The objective is to transmit flow successfully between the source and the sink nodes. The reliability of the capacity vector of the assigned components is used an indicator to find the best flow strategy on the network. The Components Assignment Problem (CAP) deals with searching the optimal components to a given network subject to one or more constraints. The CAP in multi-source multi-sink stochastic flow networks with multiple commodities has not yet been discussed, so our paper investigates this scenario to maximize the reliability of the capacity vector subject to an assignment budget. The mathematical formulation of the problem is defined, and a proposed solution based on genetic algorithms is developed consisting of two steps. The first searches the set of components with the minimum cost and the second searches the flow vector of this set of components with maximum reliability. We apply the solution approach to three commonly used examples from the literature with two sets of available components to demonstrate its strong performance.

International Journal of Network Management

Hamed Alazemi

Michael Todinov

A framework for topology optimization of repairable flow networks and reliability networks is presented. The optimization consists of determining the optimal network topology with a maximum transmitted flow achieved within a specified budget for building the network. A method for a topology optimization of reliability networks of safety-critical systems has also been developed. The proposed method solves the important problem related to how to build within a fixed budget the system characterised by the smallest risk of failure. Both methods are based on pruning the full complexity network by using the bound and branch method as a way of exploring possible network topologies. The methods have a superior running time compared to methods based on a full exhaustive search. A method has also been developed for assessing the threshold flow rate reliability of repairable flow networks with complex topology. The method is based on estimating the probability that the output flow will be equa...

Journal of Computer Science

Abdelhamid DAAMOUCHE

Aswan University Journal of Sciences and Technology

Samer Lahoud

Human-centric Computing and Information Sciences

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

Braess Paradox in Optimal Multiperiod Resource-Constrained Restoration Scheduling Problem

Research paper
Published: 04 April 2024

Cite this article

Juanjuan Lin ORCID: orcid.org/0000-0001-6778-4311 1 , 2 ,
Qizhou Hu 1 &
Yu Jiang 3 , 4

This study examines the Braess paradox in the context of the multiple-period restoration scheduling problem. A bilevel programming model is devised, where the upper-level problem is to determine the optimal sequence of recovery activities considering the limited resource constraint, while the low-level problem is the traffic assignment model that captures passengers’ responses to the changes in the transportation network capacity. Then, a novel genetic algorithm (GA) is developed to solve the proposed restoration scheduling problem. Our case study first shows that the optimal restoration schedule does not concur with the results obtained based on the link importance measurement, and the former can achieve a 4% total travel time reduction compared with the latter. Then, various numerical experiments are conducted to illustrate the occurrence and properties of the Braess paradox, which is that the network performance in some restoration periods can be better than that before the disruption or after a disrupted link is recovered. Moreover, it is revealed that with sufficient resources for multiple links to be repaired simultaneously, it is unnecessary to do so in the optimal rehabilitation schedule due to the existence of the Braess paradox. Finally, in terms of algorithmic performance, our proposed-GA outperforms the particle swarm optimisation algorithm and can reduce the computation time by up to 14%.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Data availability

The data that support the findings of this study are available on request from the corresponding author.

Liu K, Zhai C, Dong Y (2020) Optimal restoration schedules of transportation network considering resilience. Struct Infrastruct Eng 17(8):1141–1154

Article Google Scholar

Sun W, Bocchini P, Davison BD (2020) Resilience metrics and measurement methods for transportation infrastructure: the state of the art. Sustain Resil Infrastruct 5(3):168–199

Zhou Y, Wang J, Yang H (2019) Resilience of transportation systems: concepts and comprehensive review. IEEE T Intell Transp Syst 20(12):4262–4276

Zhang X, Mahadevan S, Sankararaman S, Goebel K (2018) Resilience-based network design under uncertainty. Reliab Eng Syst Saf 169:364–379

Jiang Y, Wang Y, Szeto WY, Chow AHF, Nagurney A (2020) Probabilistic assessment of transport network vulnerability with equilibrium flows. Int J Sustain Transp 15(7):512–523

Zhang W, Wang N, Nicholson C (2017) Resilience-based post-disaster recovery strategies for road-bridge networks. Struct Infrastruct Eng 13(11):1404–1413

Holling CS (1973) Resilience and stability of ecological systems. Annu Rev Ecol Syst 4:1–23

Gu Y, Fu X, Liu Z, Xu X, Chen A (2020) Performance of transportation network under perturbations: reliability, vulnerability, and resilience. Transp Res Part E: Logist Transp Rev 133:101809

Zhang X, Miller-Hooks E, Denny K (2015) Assessing the role of network topology in transportation network resilience. J Transp Geogr 46:35–45

Aydin NY, Duzgun HS, Wenzel F, Heinimann HR (2017) Integration of stress testing with graph theory to assess the resilience of urban road networks under seismic hazards. Nat Hazards 91(1):37–68

Dunn S, Wilkinson SM (2016) Increasing the resilience of air traffic networks using a network graph theory approach. Transp Res Part E: Logist Transp Rev 90:39–50

Zhou J, Coit DW, Felder FA, Wang D (2021) Resiliency-based restoration optimization for dependent network systems against cascading failures. Reliab Eng Syst Saf 207:107383

Berche B, Von Ferber C, Holovatch T, Holovatch Y (2009) Resilience of public transport networks against attacks. Eur Phys J B 71(1):125–137

Zhang W, Wang N (2016) Resilience-based risk mitigation for road networks. Struct Saf 62:57–65

Osei-Asamoah A, Lownes NE (2014) Complex network method of evaluating resilience in surface transportation networks. Transport Res Rec 2467(1):120–128

Karamlou A, Bocchini P (2016) Sequencing algorithm with multiple-input genetic operators: application to disaster resilience. Eng Struct 117:591–602

Kaviani A, Thompson RG, Rajabifard A, Sarvi M (2018) A model for multi-class road network recovery scheduling of regional road networks. Transportation 47(1):109–143

Yoon S, Suh W, Lee YJ (2021) Optimal decision making in post-hazard bridge recovery strategies for transportation networks after seismic events. Geomat Nat Haz Risk 12(1):2629–2653

Wu Y, Hou G, Chen S (2021) Post-earthquake resilience assessment and long-term restoration prioritization of transportation network. Reliab Eng Syst Saf 211:107612

Gokalp C, Patil PN, Boyles SD (2021) Post-disaster recovery sequencing strategy for road networks. Transp Res Part B: Methodol 153:228–245

Fang Y, Sansavini G (2019) Optimum post-disruption restoration under uncertainty for enhancing critical infrastructure resilience. Reliab Eng Syst Saf 185:1–11

Bocchini P, Frangopol DM (2012) Optimal resilience- and cost-based post-disaster intervention prioritization for bridges along a highway segment. J Bridge Eng 17(1):117–129

Liu J, Schonfeld PM, Zhan S, Wang KCP, Peng Q (2022) Reducing an urban rail transit network’s passenger-oriented vulnerability by adding turn-back tracks. Transportmetrica B 10(1):667–692

Google Scholar

Gauthier P, Furno A, El Faouzi NE (2018) Road network resilience: how to identify critical links subject to day-to-day disruptions. Transport Res Rec 2672(1):54–65

Cox A, Prager F, Rose A (2011) Transportation security and the role of resilience: a foundation for operational metrics. Transp Policy 18(2):307–317

Sun W, Bocchini P, Davison BD (2021) Policy-based disaster recovery planning model for interdependent infrastructure systems under uncertainty. Struct Infrastruct Eng 17(4):555–578

Somy S, Shafaei R, Ramezanian R (2021) Resilience-based mathematical model to restore disrupted road-bridge transportation networks. Struct Infrastruct Eng 18(9):1334–1349

Ye Q, Ukkusuri SV (2014) Resilience as an objective in the optimal reconstruction sequence for transportation networks. J Transp Saf Secur 7(1):91–105

Zhang C, Kong J, Simonovic SP (2018) Restoration resource allocation model for enhancing resilience of interdependent infrastructure systems. Saf Sci 102:169–177

Kusumastuti RD, Husodo ZA, Suardi L, Danarsari DN (2014) Developing a resilience index towards natural disasters in Indonesia. Int J Disaster Risk Reduct 10:327–340

Merschman E, Doustmohammadi M, Salman AM, Anderson M (2020) Post-disaster decision framework for bridge repair prioritization to improve road network resilience. Transport Res Rec 2674(3):81–92

Li Z, Jin C, Hu P, Wang C (2019) Resilience-based transportation network recovery strategy during emergency recovery phase under uncertainty. Reliab Eng Syst Saf 188:503–514

Sohouenou PYR, Neves LAC (2021) Assessing the effects of link-repair sequences on road network resilience. Int J Crit Infr Prot 34:100448

Rey D, Bar-Gera H (2020) Long-term scheduling for road network disaster recovery. Int J Disaster Risk Reduct 42:101353

Liu Y, Mcneil S, Hackl J, Adey BT (2020) Prioritizing transportation network recovery using a resilience measure. Sustain Resil Infrastruct 7(1):70–81

Braess D, Nagurney A, Wakolbinger T (2005) On a paradox of traffic planning. Transp Sci 39(4):446–450

Bagloee SA, Ceder AA, Sarvi M, Asadi M (2019) Is it time to go for no-car zone policies? Braess Paradox detection. Transp Res Part A: Policy Pract 121:251–264

Jiang Y, Rasmussen TK, Nielsen OA (2022) Integrated optimization of transit networks with schedule-and frequency-based services subject to the bounded stochastic user equilibrium. Transp Sci 56(6):1452–1468

Ye J, Jiang Y, Chen J, Liu Z, Guo R (2021) Joint optimization of transfer location and capacity for a capacitated multimodal transport network with elastic demand: a bi-level programming model and paradoxes. Transp Res Part E: Logist Transp Rev 156:102540

Yao J, Cheng Z, Dai J, Chen A, An S (2019) Traffic assignment paradox incorporating congestion and stochastic perceived error simultaneously. Transportmetrica A: Transp Sci 15(2):307–325

Jiang Y, Szeto WY (2016) Reliability-based stochastic transit assignment: formulations and capacity paradox. Transp Res Part B: Methodol 93:181–206

Szeto WY, Jiang Y (2014) Transit assignment: approach-based formulation, extragradient method, and paradox. Transp Res Part B: Methodol 62:51–76

Szeto WY, Wang Y, Wong SC (2014) The chemical reaction optimization approach to solving the environmentally sustainable network design problem. Comput Aided Civ Infrastruct Eng 29(2):140–158

Beckmann MJ, McGuire CB, Winsten CB (1956) Studies in the economics of transportation. Yale University, New Haven

Sheffi Y (1985) Urban transportation networks: Equilibrium analysis with mathematical programming methods. Prentice-Hall, New Jersey

Magnanti TL, Wong RT (1984) Network design and transportation planning: models and algorithms. Transp Sci 18(1):1–55

Shayanfar E, Schonfeld P (2019) Selecting and scheduling interrelated road projects with uncertain demand. Transportmetrica A: Transp Sci 15(2):1712–1733

Jiang Y (2022) Reliability-based equitable transit frequency design. Transportmetrica A: Transp Sci 18(3):879–909

Calvete HI, Galé C, Oliveros MJ (2011) Bilevel model for production-distribution planning solved by using ant colony optimization. Comput Oper Res 38(1):320–327

Roca-Riu M, Estrada M, Trapote C (2012) The design of interurban bus networks in city centers. Transp Res Part A: Policy Pract 46(8):1153–1165

Hackl J, Adey BT, Lethanh N (2018) Determination of near-optimal restoration programs for transportation networks following natural hazard events using simulated annealing. Comput Aided Civ Infrastruct Eng 33(8):618–637

Qiang Q, Nagurney A (2007) A unified network performance measure with importance identification and the ranking of network components. Optim Lett 2(1):127–142

Article MathSciNet Google Scholar

Download references

Acknowledgements

The authors are grateful to the anonymous reviewers for their constructive comments. This research is supported by the Scholarship Fund of China Scholarship Council (CSC No. 202006840084) , the National Natural Science Foundation of China (Grant No. 51178157) and the Key Science and Technology Program of Henan Province (Grant No. 182102310004).

Author information

Authors and affiliations.

School of Automation, Nanjing University of Science and Technology, Nanjing, China

Juanjuan Lin & Qizhou Hu

School of Urban Construction and Design, Taizhou Institute of Science and Technology, Nanjing University of Science and Technology, Taizhou, China

Juanjuan Lin

DTU Management, Technical University of Denmark, Copenhagen, Denmark

Lancaster University Management School, Lancaster University, Lancaster, UK

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Juanjuan Lin .

Ethics declarations

Conflict of interest.

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Lin, J., Hu, Q. & Jiang, Y. Braess Paradox in Optimal Multiperiod Resource-Constrained Restoration Scheduling Problem. Int J Civ Eng (2024). https://doi.org/10.1007/s40999-024-00963-4

Download citation

Received : 19 July 2023

Revised : 02 February 2024

Accepted : 07 March 2024

Published : 04 April 2024

DOI : https://doi.org/10.1007/s40999-024-00963-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Braess paradox
Traffic assignment
Bilevel network design
Network resilience
Restoration scheduling
Find a journal
Publish with us
Track your research

Help | Advanced Search

Mathematics > Optimization and Control

Title: hub network design problem with capacity, congestion and heterogeneous economies of scale.

Abstract: We propose a joint model that links the strategic level location and capacity decisions with the operational level routing and hub assignment decisions to solve hub network design problem with congestion and heterogeneous economics of scale. We also develop a novel flow-based mixed-integer second-order cone programming (MISOCP) formulation. We perform numerical experiments on a real-world data set to validate the efficiency of solving the MISOCP reformulation. The numerical studies yield observations can be used as guidelines in the design of transportation network for a logistics company.

Submission history

Access paper:.

Other Formats

References & Citations

Google Scholar
Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

IMAGES

Solved following problems for the given network. Capacity
Network Capacity Planning 101: Best Practices & Tutorial
What Determines The Capacity Of A Network?
What Is Network Capacity Planning?
Best Network Capacity Planning Tools + Guide
Network Capacity Planning 101: Requirements & Best Practices

VIDEO

Week 4
NPTEL Assignment|Week 9 solution|Network Analysis@shivasaiforyou-basicelectr1790
CS304 Assignment No.2 spring 2023 100% Correct Complete Solution BY Learning With Happy Mood|CS304
CS407 Routing and Switching
NPTEL Assignment|Week 8 solution|@ network analysis@shivasaiforyou-basicelectr1790
NPTEL Assignment|Week 6|solution|Network Analysis@shivasaiforyou-basicelectr1790

COMMENTS

On Solving the Capacity Assignment Problem Using Continuous ...
The Capacity Assignment problem focuses on finding the best possible set of capacities for the links that satisfy the traffic requirements in a prioritized network while minimizing the cost. Apart from the traditional methods for solving this NP-Hard problem, one new method that uses Learning Automata (LA) strategies has been recently reported.
Network flow problem
The network flow problem can be conceptualized as a directed graph which abides by flow capacity and conservation constraints. The vertices in the graph are classified into origins (source X {\displaystyle X} ), destinations (sink O {\displaystyle O} ), and intermediate points and are collectively referred to as nodes ( N {\displaystyle N} ).
Chapter 5 Capacity Assignment Problems
Chapter 5 Capacity Assignment Problems 5.1 Introduction. Given a network topology , with the set of nodes and the set of links, the capacity assignment problem decides on the capacity allocated to each link .This problem appears in two main (quite diverse) contexts: (i) as a problem to be solved periodically at long time scales (e.g., every 6 months) to upgrade the capacity of deployed links ...
PDF Chapter 5 Network Flows
is a min-cost-ﬂow problem, basic feasible solutions assign integer values to variables. Hence, this formulation addresses the requirement that units of inventory are indivisible. 5.2.3 Assignment Problems The assignment problem involves allocating a number of jobs to workers in some optimal manner. A simple example should be suﬃcient to ...
On The Bottleneck and Capacity Assignment Problems
this paper we investigate the capacity and oottleneck assignment problems (we further. refer to them as CAP and BAP respectively) in a probabilistic framework. [GG,AV). These problems can be formulated as follows. Let. A = {ajj}fJ=1 be a. n. x n matrix of real numbers which we further call. weights. In. the bottleneck (capacity) assignment ...
Capacity Assignment Problems
This chapter is devoted to capacity assignment problems in two contexts: (i) long‐term capacity planning where link capacities are upgraded, for example every 6 months to match a forecasted traffic growth, (ii) fast capacity allocation in wireless networks, where capacities are updated at a subsecond rate to adapt to varying network conditions by adjusting transmission power or access ...
Capacity assignment in multiservice packet networks with soft maximum
The problem of capacity assignment has been addressed in the literature for various network scenarios with different objectives. The studies in Verma et al. (1998), Diwan et al. (2002) and Choi (2008) address the problem of capacity assignment with hard end-to-end delay
Optimising capacity assignment in multiservice MPLS networks
In the capacity assignment problem (Gerla, 1975; Maruyama & Tang, 1976; Amiri, 1992) the routing protocol is understood to be given and the optimal capacity for every link is chosen from within a discrete set of line capacities. ... When the network capacity is established and the demand volume is understood, the question becomes how to assign ...
On the capacity assignment problem in packet-switching computer
On the capacity assignment problem in packet-switching computer networks E. D. Sykas Department of Electrical Engineering, National Technical UniversiO, of Athens, Scopelou 42, Athens 113 63, Greece (Received September 1984; revised FebruatT 1986) The capacity assignment problem in a packet-switching communica- tion network is examined with a new look and under general assumptions about the ...
Capacity Assignment Problems
This chapter is devoted to capacity assignment problems in two contexts: (i) long-term capacity planning where link capacities are upgraded, for example every 6 months to match a forecasted traffic growth, (ii) fast capacity allocation in wireless networks, where capacities are updated at a subsecond rate to adapt to varying network conditions by adjusting transmission power or access ...
Capacity assignment in multiservice packet networks with soft maximum
The problem of capacity assignment has been addressed in the literature for various network scenarios with different objectives. The studies in Verma et al. (1998), Diwan et al. (2002) and Choi (2008) address the problem of capacity assignment with hard end-to-end delay guarantees.
PDF A Fast and Efficient Solution to the Capacity Assignment Problem Using
integer programming problem, the details of which can be found in [12,13]. II. Previous Solutions II.1 The Marayuma -Tang Solution The Marayuma/Tang (MT-CA) solution to the Capacity Assignment (CA) problem [7] is based on several low level heuristic routines adapted for total network cost optimization.
PDF Network Flow Problems
Min-Cost Max-Flow. A variant of the max-flow problem. Each edge e has capacity c(e) and cost cost(e) You have to pay cost(e) amount of money per unit flow flowing through e. Problem: find the maximum flow that has the minimum total cost. A lot harder than the regular max-flow. - But there is an easy algorithm that works for small graphs.
PDF Transportation Network Design
5.1 Network Capacity Expansion 5.2 Combined traffic assignment and signal control 5.3 Optimising Toll 5.4 Formal Notation 6 Formulation of capacity expansion problem ... assignment problem tries to model these behaviour. Therefore, the traffic assignment will be discussed
Network capacity assignment for multicast services using genetic
Abstract: This letter focuses on the problem of network capacity assignment to accommodate the introduction of additional multicast services in existing unicast networks. The problem is firstly formalized by defining a cost function to evaluate the goodness of a given capacity allocation configuration. Then, a novel approach based on the genetic algorithms is provided to find the near-optimal ...
A Genetic Algorithm to Solve Capacity Assignment Problem in a Flow Network
The robust design problem (RDP) in a capacitated flow network is to search for the minimum capacity assignment of each edge such that the network still survived even under the edge's failure. The RDP is known as NP-hard. Thus, capacity assignment problem subject to system reliability and total capacity constraints is studied in this paper.
A Genetic Algorithm to Solve Capacity Assignment Problem in a Flow Network
The robust design problem (RDP) in a capacitated flow network is to search for the minimum capacity assignment of each edge such that the network still survived even under the edge's failure. The ...
PDF A Genetic Algorithm to Solve Capacity Assignment Problem in a Flow Network
The capacity assignment problem (CAP) is generally defined as the search for the optimal capacities that minimize the delay the network and maximize its reliability [in Zantuti (2008)].
An optimal capacity assignment for the robust design problem in
Therefore, each edge in the network should be assigned sufficient capacity to keep the network functioning normally. The robust design problem (RDP) in a capacitated flow network is to search for the minimum capacity assignment of each edge such that the network still survived even under the edge's failure.
Maximum Network Capacity Problem under the ...
This paper considers the problem of finding the maximum OD flow pattern for the capacity constrained transportaion network under the condition that the flow pattern is described by the user equilibrium assignment. We first show the theoretical relation between the network capacity problem and the particular class of equilibrium assignment models. Then, the mathematical formulation and the ...
DAA
Network Flow Problems. The most obvious flow network problem is the following: Problem1: Given a flow network G = (V, E), the maximum flow problem is to find a flow with maximum value. Problem 2: The multiple source and sink maximum flow problem is similar to the maximum flow problem, except there is a set {s 1,s 2,s 3.....s n} of sources and a set {t 1,t 2,t 3.....t n} of sinks.
A Genetic Algorithm to Solve Capacity Assignment Problem in a Flow Network
The robust design problem (RDP) in a capacitated flow network is to search for the minimum capacity assignment of each edge such that the network still survived even under the edge's failure. The RDP is known as NP-hard. Thus, capacity assignment problem subject to system reliability and total capacity constraints is studied in this paper.
Braess Paradox in Optimal Multiperiod Resource-Constrained ...
A bilevel model is formulated, where the upper-level problem is to determine the optimal restoration scheduling considering resource constraints, while the lower-level problem is the traffic assignment model that captures passengers' response to changes in network topology and capacity as a result of restoration activities.
[2404.03521] Hub Network Design Problem with Capacity, Congestion and
We propose a joint model that links the strategic level location and capacity decisions with the operational level routing and hub assignment decisions to solve hub network design problem with congestion and heterogeneous economics of scale. We also develop a novel flow-based mixed-integer second-order cone programming (MISOCP) formulation. We perform numerical experiments on a real-world data ...
Large-scale multimodal transportation network models and algorithms
Some researchers further examine the network capacity problem in the context of traffic management and control strategies, and combine the network capacity model with road toll, network design and signal control. ... In this section, we extend the traffic assignment problem for urban road network (Eqs. (10)-(13) in NCP1) to a combined mode ...