hypothesis testing assignment quizlet

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.

There are 5 main steps in hypothesis testing:

• State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a  or H 1 ).
• Collect data in a way designed to test the hypothesis.
• Perform an appropriate statistical test .
• Decide whether to reject or fail to reject your null hypothesis.
• Present the findings in your results and discussion section.

Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

Table of contents

Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.

After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.

The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.

• H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.

There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).

If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.

Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.

Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .

• an estimate of the difference in average height between the two groups.
• a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.

Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.

In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.

In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .

In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.

In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.

However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.

If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”

These are superficial differences; you can see that they mean the same thing.

You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.

If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Normal distribution
• Descriptive statistics
• Measures of central tendency
• Correlation coefficient

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved March 25, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3 hypothesis testing.

In reviewing hypothesis tests, we start first with the general idea. Then, we keep returning to the basic procedures of hypothesis testing, each time adding a little more detail.

The general idea of hypothesis testing involves:

• Making an initial assumption.
• Collecting evidence (data).
• Based on the available evidence (data), deciding whether to reject or not reject the initial assumption.

Every hypothesis test — regardless of the population parameter involved — requires the above three steps.

Example S.3.1

Is normal body temperature really 98.6 degrees f section  .

Consider the population of many, many adults. A researcher hypothesized that the average adult body temperature is lower than the often-advertised 98.6 degrees F. That is, the researcher wants an answer to the question: "Is the average adult body temperature 98.6 degrees? Or is it lower?" To answer his research question, the researcher starts by assuming that the average adult body temperature was 98.6 degrees F.

Then, the researcher went out and tried to find evidence that refutes his initial assumption. In doing so, he selects a random sample of 130 adults. The average body temperature of the 130 sampled adults is 98.25 degrees.

Then, the researcher uses the data he collected to make a decision about his initial assumption. It is either likely or unlikely that the researcher would collect the evidence he did given his initial assumption that the average adult body temperature is 98.6 degrees:

• If it is likely , then the researcher does not reject his initial assumption that the average adult body temperature is 98.6 degrees. There is not enough evidence to do otherwise.
• either the researcher's initial assumption is correct and he experienced a very unusual event;
• or the researcher's initial assumption is incorrect.

In statistics, we generally don't make claims that require us to believe that a very unusual event happened. That is, in the practice of statistics, if the evidence (data) we collected is unlikely in light of the initial assumption, then we reject our initial assumption.

Example S.3.2

Criminal trial analogy section  .

One place where you can consistently see the general idea of hypothesis testing in action is in criminal trials held in the United States. Our criminal justice system assumes "the defendant is innocent until proven guilty." That is, our initial assumption is that the defendant is innocent.

In the practice of statistics, we make our initial assumption when we state our two competing hypotheses -- the null hypothesis ( H 0 ) and the alternative hypothesis ( H A ). Here, our hypotheses are:

• H 0 : Defendant is not guilty (innocent)
• H A : Defendant is guilty

In statistics, we always assume the null hypothesis is true . That is, the null hypothesis is always our initial assumption.

The prosecution team then collects evidence — such as finger prints, blood spots, hair samples, carpet fibers, shoe prints, ransom notes, and handwriting samples — with the hopes of finding "sufficient evidence" to make the assumption of innocence refutable.

In statistics, the data are the evidence.

The jury then makes a decision based on the available evidence:

• If the jury finds sufficient evidence — beyond a reasonable doubt — to make the assumption of innocence refutable, the jury rejects the null hypothesis and deems the defendant guilty. We behave as if the defendant is guilty.
• If there is insufficient evidence, then the jury does not reject the null hypothesis . We behave as if the defendant is innocent.

In statistics, we always make one of two decisions. We either "reject the null hypothesis" or we "fail to reject the null hypothesis."

Errors in Hypothesis Testing Section  

Did you notice the use of the phrase "behave as if" in the previous discussion? We "behave as if" the defendant is guilty; we do not "prove" that the defendant is guilty. And, we "behave as if" the defendant is innocent; we do not "prove" that the defendant is innocent.

This is a very important distinction! We make our decision based on evidence not on 100% guaranteed proof. Again:

• If we reject the null hypothesis, we do not prove that the alternative hypothesis is true.
• If we do not reject the null hypothesis, we do not prove that the null hypothesis is true.

We merely state that there is enough evidence to behave one way or the other. This is always true in statistics! Because of this, whatever the decision, there is always a chance that we made an error .

Let's review the two types of errors that can be made in criminal trials:

Table S.3.2 shows how this corresponds to the two types of errors in hypothesis testing.

Note that, in statistics, we call the two types of errors by two different  names -- one is called a "Type I error," and the other is called  a "Type II error." Here are the formal definitions of the two types of errors:

There is always a chance of making one of these errors. But, a good scientific study will minimize the chance of doing so!

Making the Decision Section  

Recall that it is either likely or unlikely that we would observe the evidence we did given our initial assumption. If it is likely , we do not reject the null hypothesis. If it is unlikely , then we reject the null hypothesis in favor of the alternative hypothesis. Effectively, then, making the decision reduces to determining "likely" or "unlikely."

In statistics, there are two ways to determine whether the evidence is likely or unlikely given the initial assumption:

• We could take the " critical value approach " (favored in many of the older textbooks).
• Or, we could take the " P -value approach " (what is used most often in research, journal articles, and statistical software).

In the next two sections, we review the procedures behind each of these two approaches. To make our review concrete, let's imagine that μ is the average grade point average of all American students who major in mathematics. We first review the critical value approach for conducting each of the following three hypothesis tests about the population mean $\mu$:

In Practice

• We would want to conduct the first hypothesis test if we were interested in concluding that the average grade point average of the group is more than 3.
• We would want to conduct the second hypothesis test if we were interested in concluding that the average grade point average of the group is less than 3.
• And, we would want to conduct the third hypothesis test if we were only interested in concluding that the average grade point average of the group differs from 3 (without caring whether it is more or less than 3).

Upon completing the review of the critical value approach, we review the P -value approach for conducting each of the above three hypothesis tests about the population mean \(\mu\). The procedures that we review here for both approaches easily extend to hypothesis tests about any other population parameter.

Module 8: Inference for One Proportion

Hypothesis testing (1 of 5), learning outcomes.

• When testing a claim, distinguish among situations involving one population mean, one population proportion, two population means, or two population proportions.
• Given a claim about a population, determine null and alternative hypotheses.

Introduction

In inference, we use a sample to draw a conclusion about a population. Two types of inference are the focus of our work in this course:

• Estimate a population parameter with a confidence interval.
• Test a claim about a population parameter with a hypothesis test.

We can also use samples from two populations to compare those populations. In this situation, the two types of inference focus on differences in the parameters.

• Estimate a difference in population parameters with a confidence interval.
• Test a claim about a difference in population parameters with a hypothesis test.

In “Estimating a Population Proportion,” we learned to estimate a population proportion using a confidence interval. For example, we estimated the proportion of all Tallahassee Community College students who are female and the proportion of all American adults who used the Internet to obtain medical information in the previous month. We will revisit confidence intervals in future modules.

Now we look more carefully at how to test a claim with a hypothesis test. Statistical investigations begin with research questions. We begin our discussion of hypothesis tests with research questions that require us to test a claim. Later we look at how a claim becomes a hypothesis.

Research Questions about Testing Claims

Let’s revisit some of the research questions from examples in the module Types of Statistical Studies and Producing Data that involve testing a claim.

Is the average course load for community college students less than 12 semester hours? This question contains a claim about a population mean. The question contains information about the population, the variable, and the parameter. The population is all community college students. The variable is course load in semester hours . It is quantitative, so the parameter is a mean. The claim is, “The mean course load for all community college students is less than 12 semester hours.”

Do the majority of community college students qualify for federal student loans? This question contains a claim about a population proportion and information about the population, the variable, and the parameter. The population is all community college students. The variable is Qualify for federal student loan (yes or no). It is categorical, so the parameter is a proportion. The claim is, “The proportion of community college students who qualify is greater than 0.5” (a majority means more than half, or 0.5).

In community colleges, do female students and male students have different mean GPAs? This question contains a claim that compares two population means. Again, we see information about the populations, the variable, and the parameters. The two populations are female community college students and male community college students. The variable is GPA . It is quantitative, so the parameters are means. The claim is, “The mean GPA for female community college students is different from the mean GPA for male community college students.” Notice that the claim compares the two population means, but there is no claim about the numeric value of either mean.

Are college athletes more likely than nonathletes to receive academic advising? This question contains a claim that compares two population proportions: college athletes and college students who are not athletes. The variable is Receive academic advising (yes or no). The variable is categorical, so the parameters are proportions. The claim is, “The proportion of all college athletes who receive academic advising is greater than the proportion of all nonathletes in college who receive academic advising.” Notice that the claim compares two population proportions, but there is no claim about the numeric value of either proportion.

In the case of testing a claim about a single population parameter, we compare it to a numeric value. In the case of testing a claim about two population parameters, we compare them to each other.

Identify the type of claim in each research question below.

Next Steps: Forming Hypotheses

We already know that in inference we use a sample to draw a conclusion about a population. If the research question contains a claim about the population, we translate the claim into two related hypotheses.

The null hypothesis is a hypothesis about the value of the parameter. The null hypothesis relates to our work in Linking Probability to Statistical Inference where we drew a conclusion about a population parameter on the basis of the sampling distribution. We started with an assumption about the value of the parameter, then used a simulation to simulate the selection of random samples from a population with this parameter value. Or we used the parameter value in a mathematical model to describe the center and spread of the sampling distribution. The null hypothesis gives the value of the parameter that we will use to create the sampling distribution. In this way, the null hypothesis states what we assume to be true about the population.

The alternative hypothesis usually reflects the claim in the research question about the value of the parameter. The alternative hypothesis says the parameter is “greater than” or “less than” or “not equal to” the value we assume to true in the null hypothesis.

Stating Hypotheses

Here are the hypotheses for the research questions from the previous example. The null hypothesis is abbreviated H 0 . The alternative hypothesis is abbreviated H a .

Is the average course load for community college students less than 12 semester hours?

• H 0 : The mean course load for community college students is equal to 12 semester hours.
• H a : The mean course load for community college students is less than 12 semester hours.

Do the majority of community college students qualify for federal student loans?

• H 0 : The proportion of community college students who qualify for federal student loans is 0.5.
• H a : The proportion of community college students who qualify for federal student loans is greater than 0.5.

When the research question contains a claim that compares two populations, the null hypothesis states that the parameters are equal. We will see in Modules 9 and 10 that we translate the null hypothesis into a statement about “no difference” in parameter values. We revisit this idea in more depth later.

In community colleges, do female students and male students have different mean GPAs?

• H 0 : In community colleges, female and male students have the same mean GPAs.
• H a : In community colleges, female and male students have different mean GPAs.

Are college athletes more likely than nonathletes to receive academic advising?

• H 0 : In colleges, the proportion of athletes who receive academic advising is equal to the proportion of nonathletes who receive academic advising.
• H a : In colleges, the proportion of athletes who receive academic advising is greater than the proportion of nonathletes who receive academic advising.

Here are some general observations about null and alternative hypotheses.

• The hypotheses are competing claims about the parameter or about the comparison of parameters.
• Both hypotheses are statements about the same population parameter or same two population parameters.
• The null hypothesis contains an equal sign.
• The alternative hypothesis is always an inequality statement. It contains a “less than” or a “greater than” or a “not equal to” symbol.
• In a statistical investigation, we determine the research question, and thus the hypotheses, before we collect data.

The process of forming hypotheses, collecting data, and using the data to draw a conclusion about the hypotheses is called hypothesis testing .

Contribute!

Improve this page Learn More

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

• Quality Improvement
• Talk To Minitab

Understanding Hypothesis Tests: Why We Need to Use Hypothesis Tests in Statistics

Topics: Hypothesis Testing , Data Analysis , Statistics

Hypothesis testing is an essential procedure in statistics. A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. When we say that a finding is statistically significant, it’s thanks to a hypothesis test. How do these tests really work and what does statistical significance actually mean?

In this series of three posts, I’ll help you intuitively understand how hypothesis tests work by focusing on concepts and graphs rather than equations and numbers. After all, a key reason to use statistical software like Minitab is so you don’t get bogged down in the calculations and can instead focus on understanding your results.

To kick things off in this post, I highlight the rationale for using hypothesis tests with an example.

The Scenario

An economist wants to determine whether the monthly energy cost for families has changed from the previous year, when the mean cost per month was $260. The economist randomly samples 25 families and records their energy costs for the current year. (The data for this example is FamilyEnergyCost and it is just one of the many data set examples that can be found in Minitab’s Data Set Library.)

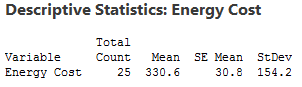
I’ll use these descriptive statistics to create a probability distribution plot that shows you the importance of hypothesis tests. Read on!

The Need for Hypothesis Tests

Why do we even need hypothesis tests? After all, we took a random sample and our sample mean of 330.6 is different from 260. That is different, right? Unfortunately, the picture is muddied because we’re looking at a sample rather than the entire population.

Sampling error is the difference between a sample and the entire population. Thanks to sampling error, it’s entirely possible that while our sample mean is 330.6, the population mean could still be 260. Or, to put it another way, if we repeated the experiment, it’s possible that the second sample mean could be close to 260. A hypothesis test helps assess the likelihood of this possibility!

Use the Sampling Distribution to See If Our Sample Mean is Unlikely

For any given random sample, the mean of the sample almost certainly doesn’t equal the true mean of the population due to sampling error. For our example, it’s unlikely that the mean cost for the entire population is exactly 330.6. In fact, if we took multiple random samples of the same size from the same population, we could plot a distribution of the sample means.

A sampling distribution is the distribution of a statistic, such as the mean, that is obtained by repeatedly drawing a large number of samples from a specific population. This distribution allows you to determine the probability of obtaining the sample statistic.

Fortunately, I can create a plot of sample means without collecting many different random samples! Instead, I’ll create a probability distribution plot using the t-distribution , the sample size, and the variability in our sample to graph the sampling distribution.

Our goal is to determine whether our sample mean is significantly different from the null hypothesis mean. Therefore, we’ll use the graph to see whether our sample mean of 330.6 is unlikely assuming that the population mean is 260. The graph below shows the expected distribution of sample means.

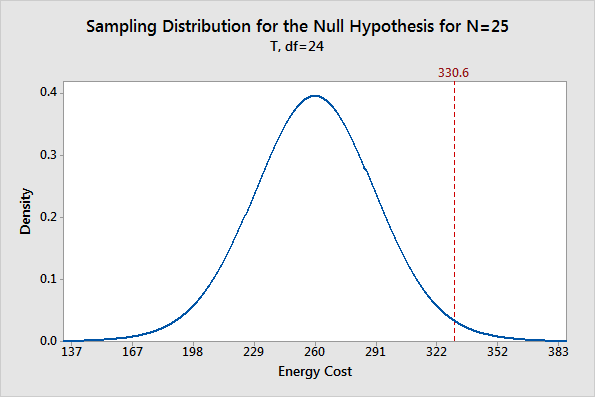
You can see that the most probable sample mean is 260, which makes sense because we’re assuming that the null hypothesis is true. However, there is a reasonable probability of obtaining a sample mean that ranges from 167 to 352, and even beyond! The takeaway from this graph is that while our sample mean of 330.6 is not the most probable, it’s also not outside the realm of possibility.

The Role of Hypothesis Tests

We’ve placed our sample mean in the context of all possible sample means while assuming that the null hypothesis is true. Are these results statistically significant?

As you can see, there is no magic place on the distribution curve to make this determination. Instead, we have a continual decrease in the probability of obtaining sample means that are further from the null hypothesis value. Where do we draw the line?

This is where hypothesis tests are useful. A hypothesis test allows us quantify the probability that our sample mean is unusual.

For this series of posts, I’ll continue to use this graphical framework and add in the significance level, P value, and confidence interval to show how hypothesis tests work and what statistical significance really means.

• Part Two: Significance Levels (alpha) and P values
• Part Three: Confidence Intervals and Confidence Levels

If you'd like to see how I made these graphs, please read: How to Create a Graphical Version of the 1-sample t-Test .

You Might Also Like

• Trust Center

© 2023 Minitab, LLC. All Rights Reserved.

• Terms of Use
• Privacy Policy
• Cookies Settings

Statistics Made Easy

How to Write Hypothesis Test Conclusions (With Examples)

A   hypothesis test is used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we reject the null hypothesis .

Otherwise, if the p-value is not less than some significance level then we fail to reject the null hypothesis .

When writing the conclusion of a hypothesis test, we typically include:

• Whether we reject or fail to reject the null hypothesis.
• The significance level.
• A short explanation in the context of the hypothesis test.

For example, we would write:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that…

Or, we would write:

We fail to reject the null hypothesis at the 5% significance level.   There is not sufficient evidence to support the claim that…

The following examples show how to write a hypothesis test conclusion in both scenarios.

Example 1: Reject the Null Hypothesis Conclusion

Suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test at a 5% significance level using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

Suppose the p-value of the test turns out to be 0.002.

Here is how she would report the results of the hypothesis test:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that this particular fertilizer causes plants to grow more during a one-month period than they normally do.

Example 2: Fail to Reject the Null Hypothesis Conclusion

Suppose the manager of a manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, he measures the mean number of defective widgets produced before and after using the new method for one month.

He performs a hypothesis test at a 10% significance level using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

Suppose the p-value of the test turns out to be 0.27.

Here is how he would report the results of the hypothesis test:

We fail to reject the null hypothesis at the 10% significance level.   There is not sufficient evidence to support the claim that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing 4 Examples of Hypothesis Testing in Real Life How to Write a Null Hypothesis

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Search code, repositories, users, issues, pull requests...

Provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications

Hypothesis Testing Assignment

santhoshprince93/Hypothesis-Testing-Assignment

Folders and files, repository files navigation, hypothesis-testing-assignment.

A F&B manager wants to determine whether there is any significant difference in the diameter of the cutlet between two units. A randomly selected sample of cutlets was collected from both units and measured? Analyze the data and draw inferences at 5% significance level. Please state the assumptions and tests that you carried out to check validity of the assumptions.

Minitab File : Cutlets.mtw

A hospital wants to determine whether there is any difference in the average Turn Around Time (TAT) of reports of the laboratories on their preferred list. They collected a random sample and recorded TAT for reports of 4 laboratories. TAT is defined as sample collected to report dispatch.

Analyze the data and determine whether there is any difference in average TAT among the different laboratories at 5% significance level.     Minitab File: LabTAT.mtw

Sales of products in four different regions is tabulated for males and females. Find if male-female buyer rations are similar across regions. TeleCall uses 4 centers around the globe to process customer order forms. They audit a certain % of the customer order forms. Any error in order form renders it defective and has to be reworked before processing. The manager wants to check whether the defective % varies by centre. Please analyze the data at 5% significance level and help the manager draw appropriate inferences

Minitab File: CustomerOrderForm.mtw  

• Jupyter Notebook 100.0%

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.4: Basic Concepts of Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 1715

• John H. McDonald
• University of Delaware

Learning Objectives

• One of the main goals of statistical hypothesis testing is to estimate the \(P\) value, which is the probability of obtaining the observed results, or something more extreme, if the null hypothesis were true. If the observed results are unlikely under the null hypothesis, reject the null hypothesis.
• Alternatives to this "frequentist" approach to statistics include Bayesian statistics and estimation of effect sizes and confidence intervals.

Introduction

There are different ways of doing statistics. The technique used by the vast majority of biologists, and the technique that most of this handbook describes, is sometimes called "frequentist" or "classical" statistics. It involves testing a null hypothesis by comparing the data you observe in your experiment with the predictions of a null hypothesis. You estimate what the probability would be of obtaining the observed results, or something more extreme, if the null hypothesis were true. If this estimated probability (the \(P\) value) is small enough (below the significance value), then you conclude that it is unlikely that the null hypothesis is true; you reject the null hypothesis and accept an alternative hypothesis.

Many statisticians harshly criticize frequentist statistics, but their criticisms haven't had much effect on the way most biologists do statistics. Here I will outline some of the key concepts used in frequentist statistics, then briefly describe some of the alternatives.

Null Hypothesis

The null hypothesis is a statement that you want to test. In general, the null hypothesis is that things are the same as each other, or the same as a theoretical expectation. For example, if you measure the size of the feet of male and female chickens, the null hypothesis could be that the average foot size in male chickens is the same as the average foot size in female chickens. If you count the number of male and female chickens born to a set of hens, the null hypothesis could be that the ratio of males to females is equal to a theoretical expectation of a \(1:1\) ratio.

The alternative hypothesis is that things are different from each other, or different from a theoretical expectation.

For example, one alternative hypothesis would be that male chickens have a different average foot size than female chickens; another would be that the sex ratio is different from \(1:1\).

Usually, the null hypothesis is boring and the alternative hypothesis is interesting. For example, let's say you feed chocolate to a bunch of chickens, then look at the sex ratio in their offspring. If you get more females than males, it would be a tremendously exciting discovery: it would be a fundamental discovery about the mechanism of sex determination, female chickens are more valuable than male chickens in egg-laying breeds, and you'd be able to publish your result in Science or Nature . Lots of people have spent a lot of time and money trying to change the sex ratio in chickens, and if you're successful, you'll be rich and famous. But if the chocolate doesn't change the sex ratio, it would be an extremely boring result, and you'd have a hard time getting it published in the Eastern Delaware Journal of Chickenology . It's therefore tempting to look for patterns in your data that support the exciting alternative hypothesis. For example, you might look at \(48\) offspring of chocolate-fed chickens and see \(31\) females and only \(17\) males. This looks promising, but before you get all happy and start buying formal wear for the Nobel Prize ceremony, you need to ask "What's the probability of getting a deviation from the null expectation that large, just by chance, if the boring null hypothesis is really true?" Only when that probability is low can you reject the null hypothesis. The goal of statistical hypothesis testing is to estimate the probability of getting your observed results under the null hypothesis.

Biological vs. Statistical Null Hypotheses

It is important to distinguish between biological null and alternative hypotheses and statistical null and alternative hypotheses. "Sexual selection by females has caused male chickens to evolve bigger feet than females" is a biological alternative hypothesis; it says something about biological processes, in this case sexual selection. "Male chickens have a different average foot size than females" is a statistical alternative hypothesis; it says something about the numbers, but nothing about what caused those numbers to be different. The biological null and alternative hypotheses are the first that you should think of, as they describe something interesting about biology; they are two possible answers to the biological question you are interested in ("What affects foot size in chickens?"). The statistical null and alternative hypotheses are statements about the data that should follow from the biological hypotheses: if sexual selection favors bigger feet in male chickens (a biological hypothesis), then the average foot size in male chickens should be larger than the average in females (a statistical hypothesis). If you reject the statistical null hypothesis, you then have to decide whether that's enough evidence that you can reject your biological null hypothesis. For example, if you don't find a significant difference in foot size between male and female chickens, you could conclude "There is no significant evidence that sexual selection has caused male chickens to have bigger feet." If you do find a statistically significant difference in foot size, that might not be enough for you to conclude that sexual selection caused the bigger feet; it might be that males eat more, or that the bigger feet are a developmental byproduct of the roosters' combs, or that males run around more and the exercise makes their feet bigger. When there are multiple biological interpretations of a statistical result, you need to think of additional experiments to test the different possibilities.

Testing the Null Hypothesis

The primary goal of a statistical test is to determine whether an observed data set is so different from what you would expect under the null hypothesis that you should reject the null hypothesis. For example, let's say you are studying sex determination in chickens. For breeds of chickens that are bred to lay lots of eggs, female chicks are more valuable than male chicks, so if you could figure out a way to manipulate the sex ratio, you could make a lot of chicken farmers very happy. You've fed chocolate to a bunch of female chickens (in birds, unlike mammals, the female parent determines the sex of the offspring), and you get \(25\) female chicks and \(23\) male chicks. Anyone would look at those numbers and see that they could easily result from chance; there would be no reason to reject the null hypothesis of a \(1:1\) ratio of females to males. If you got \(47\) females and \(1\) male, most people would look at those numbers and see that they would be extremely unlikely to happen due to luck, if the null hypothesis were true; you would reject the null hypothesis and conclude that chocolate really changed the sex ratio. However, what if you had \(31\) females and \(17\) males? That's definitely more females than males, but is it really so unlikely to occur due to chance that you can reject the null hypothesis? To answer that, you need more than common sense, you need to calculate the probability of getting a deviation that large due to chance.

In the figure above, I used the BINOMDIST function of Excel to calculate the probability of getting each possible number of males, from \(0\) to \(48\), under the null hypothesis that \(0.5\) are male. As you can see, the probability of getting \(17\) males out of \(48\) total chickens is about \(0.015\). That seems like a pretty small probability, doesn't it? However, that's the probability of getting exactly \(17\) males. What you want to know is the probability of getting \(17\) or fewer males. If you were going to accept \(17\) males as evidence that the sex ratio was biased, you would also have accepted \(16\), or \(15\), or \(14\),… males as evidence for a biased sex ratio. You therefore need to add together the probabilities of all these outcomes. The probability of getting \(17\) or fewer males out of \(48\), under the null hypothesis, is \(0.030\). That means that if you had an infinite number of chickens, half males and half females, and you took a bunch of random samples of \(48\) chickens, \(3.0\%\) of the samples would have \(17\) or fewer males.

This number, \(0.030\), is the \(P\) value. It is defined as the probability of getting the observed result, or a more extreme result, if the null hypothesis is true. So "\(P=0.030\)" is a shorthand way of saying "The probability of getting \(17\) or fewer male chickens out of \(48\) total chickens, IF the null hypothesis is true that \(50\%\) of chickens are male, is \(0.030\)."

False Positives vs. False Negatives

After you do a statistical test, you are either going to reject or accept the null hypothesis. Rejecting the null hypothesis means that you conclude that the null hypothesis is not true; in our chicken sex example, you would conclude that the true proportion of male chicks, if you gave chocolate to an infinite number of chicken mothers, would be less than \(50\%\).

When you reject a null hypothesis, there's a chance that you're making a mistake. The null hypothesis might really be true, and it may be that your experimental results deviate from the null hypothesis purely as a result of chance. In a sample of \(48\) chickens, it's possible to get \(17\) male chickens purely by chance; it's even possible (although extremely unlikely) to get \(0\) male and \(48\) female chickens purely by chance, even though the true proportion is \(50\%\) males. This is why we never say we "prove" something in science; there's always a chance, however miniscule, that our data are fooling us and deviate from the null hypothesis purely due to chance. When your data fool you into rejecting the null hypothesis even though it's true, it's called a "false positive," or a "Type I error." So another way of defining the \(P\) value is the probability of getting a false positive like the one you've observed, if the null hypothesis is true.

Another way your data can fool you is when you don't reject the null hypothesis, even though it's not true. If the true proportion of female chicks is \(51\%\), the null hypothesis of a \(50\%\) proportion is not true, but you're unlikely to get a significant difference from the null hypothesis unless you have a huge sample size. Failing to reject the null hypothesis, even though it's not true, is a "false negative" or "Type II error." This is why we never say that our data shows the null hypothesis to be true; all we can say is that we haven't rejected the null hypothesis.

Significance Levels

Does a probability of \(0.030\) mean that you should reject the null hypothesis, and conclude that chocolate really caused a change in the sex ratio? The convention in most biological research is to use a significance level of \(0.05\). This means that if the \(P\) value is less than \(0.05\), you reject the null hypothesis; if \(P\) is greater than or equal to \(0.05\), you don't reject the null hypothesis. There is nothing mathematically magic about \(0.05\), it was chosen rather arbitrarily during the early days of statistics; people could have agreed upon \(0.04\), or \(0.025\), or \(0.071\) as the conventional significance level.

The significance level (also known as the "critical value" or "alpha") you should use depends on the costs of different kinds of errors. With a significance level of \(0.05\), you have a \(5\%\) chance of rejecting the null hypothesis, even if it is true. If you try \(100\) different treatments on your chickens, and none of them really change the sex ratio, \(5\%\) of your experiments will give you data that are significantly different from a \(1:1\) sex ratio, just by chance. In other words, \(5\%\) of your experiments will give you a false positive. If you use a higher significance level than the conventional \(0.05\), such as \(0.10\), you will increase your chance of a false positive to \(0.10\) (therefore increasing your chance of an embarrassingly wrong conclusion), but you will also decrease your chance of a false negative (increasing your chance of detecting a subtle effect). If you use a lower significance level than the conventional \(0.05\), such as \(0.01\), you decrease your chance of an embarrassing false positive, but you also make it less likely that you'll detect a real deviation from the null hypothesis if there is one.

The relative costs of false positives and false negatives, and thus the best \(P\) value to use, will be different for different experiments. If you are screening a bunch of potential sex-ratio-changing treatments and get a false positive, it wouldn't be a big deal; you'd just run a few more tests on that treatment until you were convinced the initial result was a false positive. The cost of a false negative, however, would be that you would miss out on a tremendously valuable discovery. You might therefore set your significance value to \(0.10\) or more for your initial tests. On the other hand, once your sex-ratio-changing treatment is undergoing final trials before being sold to farmers, a false positive could be very expensive; you'd want to be very confident that it really worked. Otherwise, if you sell the chicken farmers a sex-ratio treatment that turns out to not really work (it was a false positive), they'll sue the pants off of you. Therefore, you might want to set your significance level to \(0.01\), or even lower, for your final tests.

The significance level you choose should also depend on how likely you think it is that your alternative hypothesis will be true, a prediction that you make before you do the experiment. This is the foundation of Bayesian statistics, as explained below.

You must choose your significance level before you collect the data, of course. If you choose to use a different significance level than the conventional \(0.05\), people will be skeptical; you must be able to justify your choice. Throughout this handbook, I will always use \(P< 0.05\) as the significance level. If you are doing an experiment where the cost of a false positive is a lot greater or smaller than the cost of a false negative, or an experiment where you think it is unlikely that the alternative hypothesis will be true, you should consider using a different significance level.

One-tailed vs. Two-tailed Probabilities

The probability that was calculated above, \(0.030\), is the probability of getting \(17\) or fewer males out of \(48\). It would be significant, using the conventional \(P< 0.05\)criterion. However, what about the probability of getting \(17\) or fewer females? If your null hypothesis is "The proportion of males is \(17\) or more" and your alternative hypothesis is "The proportion of males is less than \(0.5\)," then you would use the \(P=0.03\) value found by adding the probabilities of getting \(17\) or fewer males. This is called a one-tailed probability, because you are adding the probabilities in only one tail of the distribution shown in the figure. However, if your null hypothesis is "The proportion of males is \(0.5\)", then your alternative hypothesis is "The proportion of males is different from \(0.5\)." In that case, you should add the probability of getting \(17\) or fewer females to the probability of getting \(17\) or fewer males. This is called a two-tailed probability. If you do that with the chicken result, you get \(P=0.06\), which is not quite significant.

You should decide whether to use the one-tailed or two-tailed probability before you collect your data, of course. A one-tailed probability is more powerful, in the sense of having a lower chance of false negatives, but you should only use a one-tailed probability if you really, truly have a firm prediction about which direction of deviation you would consider interesting. In the chicken example, you might be tempted to use a one-tailed probability, because you're only looking for treatments that decrease the proportion of worthless male chickens. But if you accidentally found a treatment that produced \(87\%\) male chickens, would you really publish the result as "The treatment did not cause a significant decrease in the proportion of male chickens"? I hope not. You'd realize that this unexpected result, even though it wasn't what you and your farmer friends wanted, would be very interesting to other people; by leading to discoveries about the fundamental biology of sex-determination in chickens, in might even help you produce more female chickens someday. Any time a deviation in either direction would be interesting, you should use the two-tailed probability. In addition, people are skeptical of one-tailed probabilities, especially if a one-tailed probability is significant and a two-tailed probability would not be significant (as in our chocolate-eating chicken example). Unless you provide a very convincing explanation, people may think you decided to use the one-tailed probability after you saw that the two-tailed probability wasn't quite significant, which would be cheating. It may be easier to always use two-tailed probabilities. For this handbook, I will always use two-tailed probabilities, unless I make it very clear that only one direction of deviation from the null hypothesis would be interesting.

Reporting your results

In the olden days, when people looked up \(P\) values in printed tables, they would report the results of a statistical test as "\(P< 0.05\)", "\(P< 0.01\)", "\(P>0.10\)", etc. Nowadays, almost all computer statistics programs give the exact \(P\) value resulting from a statistical test, such as \(P=0.029\), and that's what you should report in your publications. You will conclude that the results are either significant or they're not significant; they either reject the null hypothesis (if \(P\) is below your pre-determined significance level) or don't reject the null hypothesis (if \(P\) is above your significance level). But other people will want to know if your results are "strongly" significant (\(P\) much less than \(0.05\)), which will give them more confidence in your results than if they were "barely" significant (\(P=0.043\), for example). In addition, other researchers will need the exact \(P\) value if they want to combine your results with others into a meta-analysis.

Computer statistics programs can give somewhat inaccurate \(P\) values when they are very small. Once your \(P\) values get very small, you can just say "\(P< 0.00001\)" or some other impressively small number. You should also give either your raw data, or the test statistic and degrees of freedom, in case anyone wants to calculate your exact \(P\) value.

Effect Sizes and Confidence Intervals

A fairly common criticism of the hypothesis-testing approach to statistics is that the null hypothesis will always be false, if you have a big enough sample size. In the chicken-feet example, critics would argue that if you had an infinite sample size, it is impossible that male chickens would have exactly the same average foot size as female chickens. Therefore, since you know before doing the experiment that the null hypothesis is false, there's no point in testing it.

This criticism only applies to two-tailed tests, where the null hypothesis is "Things are exactly the same" and the alternative is "Things are different." Presumably these critics think it would be okay to do a one-tailed test with a null hypothesis like "Foot length of male chickens is the same as, or less than, that of females," because the null hypothesis that male chickens have smaller feet than females could be true. So if you're worried about this issue, you could think of a two-tailed test, where the null hypothesis is that things are the same, as shorthand for doing two one-tailed tests. A significant rejection of the null hypothesis in a two-tailed test would then be the equivalent of rejecting one of the two one-tailed null hypotheses.

A related criticism is that a significant rejection of a null hypothesis might not be biologically meaningful, if the difference is too small to matter. For example, in the chicken-sex experiment, having a treatment that produced \(49.9\%\) male chicks might be significantly different from \(50\%\), but it wouldn't be enough to make farmers want to buy your treatment. These critics say you should estimate the effect size and put a confidence interval on it, not estimate a \(P\) value. So the goal of your chicken-sex experiment should not be to say "Chocolate gives a proportion of males that is significantly less than \(50\%\) ((\(P=0.015\))" but to say "Chocolate produced \(36.1\%\) males with a \(95\%\) confidence interval of \(25.9\%\) to \(47.4\%\)." For the chicken-feet experiment, you would say something like "The difference between males and females in mean foot size is \(2.45mm\), with a confidence interval on the difference of \(\pm 1.98mm\)."

Estimating effect sizes and confidence intervals is a useful way to summarize your results, and it should usually be part of your data analysis; you'll often want to include confidence intervals in a graph. However, there are a lot of experiments where the goal is to decide a yes/no question, not estimate a number. In the initial tests of chocolate on chicken sex ratio, the goal would be to decide between "It changed the sex ratio" and "It didn't seem to change the sex ratio." Any change in sex ratio that is large enough that you could detect it would be interesting and worth follow-up experiments. While it's true that the difference between \(49.9\%\) and \(50\%\) might not be worth pursuing, you wouldn't do an experiment on enough chickens to detect a difference that small.

Often, the people who claim to avoid hypothesis testing will say something like "the \(95\%\) confidence interval of \(25.9\%\) to \(47.4\%\) does not include \(50\%\), so we conclude that the plant extract significantly changed the sex ratio." This is a clumsy and roundabout form of hypothesis testing, and they might as well admit it and report the \(P\) value.

Bayesian statistics

Another alternative to frequentist statistics is Bayesian statistics. A key difference is that Bayesian statistics requires specifying your best guess of the probability of each possible value of the parameter to be estimated, before the experiment is done. This is known as the "prior probability." So for your chicken-sex experiment, you're trying to estimate the "true" proportion of male chickens that would be born, if you had an infinite number of chickens. You would have to specify how likely you thought it was that the true proportion of male chickens was \(50\%\), or \(51\%\), or \(52\%\), or \(47.3\%\), etc. You would then look at the results of your experiment and use the information to calculate new probabilities that the true proportion of male chickens was \(50\%\), or \(51\%\), or \(52\%\), or \(47.3\%\), etc. (the posterior distribution).

I'll confess that I don't really understand Bayesian statistics, and I apologize for not explaining it well. In particular, I don't understand how people are supposed to come up with a prior distribution for the kinds of experiments that most biologists do. With the exception of systematics, where Bayesian estimation of phylogenies is quite popular and seems to make sense, I haven't seen many research biologists using Bayesian statistics for routine data analysis of simple laboratory experiments. This means that even if the cult-like adherents of Bayesian statistics convinced you that they were right, you would have a difficult time explaining your results to your biologist peers. Statistics is a method of conveying information, and if you're speaking a different language than the people you're talking to, you won't convey much information. So I'll stick with traditional frequentist statistics for this handbook.

Having said that, there's one key concept from Bayesian statistics that is important for all users of statistics to understand. To illustrate it, imagine that you are testing extracts from \(1000\) different tropical plants, trying to find something that will kill beetle larvae. The reality (which you don't know) is that \(500\) of the extracts kill beetle larvae, and \(500\) don't. You do the \(1000\) experiments and do the \(1000\) frequentist statistical tests, and you use the traditional significance level of \(P< 0.05\). The \(500\) plant extracts that really work all give you \(P< 0.05\); these are the true positives. Of the \(500\) extracts that don't work, \(5\%\) of them give you \(P< 0.05\) by chance (this is the meaning of the \(P\) value, after all), so you have \(25\) false positives. So you end up with \(525\) plant extracts that gave you a \(P\) value less than \(0.05\). You'll have to do further experiments to figure out which are the \(25\) false positives and which are the \(500\) true positives, but that's not so bad, since you know that most of them will turn out to be true positives.

Now imagine that you are testing those extracts from \(1000\) different tropical plants to try to find one that will make hair grow. The reality (which you don't know) is that one of the extracts makes hair grow, and the other \(999\) don't. You do the \(1000\) experiments and do the \(1000\) frequentist statistical tests, and you use the traditional significance level of \(P< 0.05\). The one plant extract that really works gives you P <0.05; this is the true positive. But of the \(999\) extracts that don't work, \(5\%\) of them give you \(P< 0.05\) by chance, so you have about \(50\) false positives. You end up with \(51\) \(P\) values less than \(0.05\), but almost all of them are false positives.

Now instead of testing \(1000\) plant extracts, imagine that you are testing just one. If you are testing it to see if it kills beetle larvae, you know (based on everything you know about plant and beetle biology) there's a pretty good chance it will work, so you can be pretty sure that a \(P\) value less than \(0.05\) is a true positive. But if you are testing that one plant extract to see if it grows hair, which you know is very unlikely (based on everything you know about plants and hair), a \(P\) value less than \(0.05\) is almost certainly a false positive. In other words, if you expect that the null hypothesis is probably true, a statistically significant result is probably a false positive. This is sad; the most exciting, amazing, unexpected results in your experiments are probably just your data trying to make you jump to ridiculous conclusions. You should require a much lower \(P\) value to reject a null hypothesis that you think is probably true.

A Bayesian would insist that you put in numbers just how likely you think the null hypothesis and various values of the alternative hypothesis are, before you do the experiment, and I'm not sure how that is supposed to work in practice for most experimental biology. But the general concept is a valuable one: as Carl Sagan summarized it, "Extraordinary claims require extraordinary evidence."

Recommendations

Here are three experiments to illustrate when the different approaches to statistics are appropriate. In the first experiment, you are testing a plant extract on rabbits to see if it will lower their blood pressure. You already know that the plant extract is a diuretic (makes the rabbits pee more) and you already know that diuretics tend to lower blood pressure, so you think there's a good chance it will work. If it does work, you'll do more low-cost animal tests on it before you do expensive, potentially risky human trials. Your prior expectation is that the null hypothesis (that the plant extract has no effect) has a good chance of being false, and the cost of a false positive is fairly low. So you should do frequentist hypothesis testing, with a significance level of \(0.05\).

In the second experiment, you are going to put human volunteers with high blood pressure on a strict low-salt diet and see how much their blood pressure goes down. Everyone will be confined to a hospital for a month and fed either a normal diet, or the same foods with half as much salt. For this experiment, you wouldn't be very interested in the \(P\) value, as based on prior research in animals and humans, you are already quite certain that reducing salt intake will lower blood pressure; you're pretty sure that the null hypothesis that "Salt intake has no effect on blood pressure" is false. Instead, you are very interested to know how much the blood pressure goes down. Reducing salt intake in half is a big deal, and if it only reduces blood pressure by \(1mm\) Hg, the tiny gain in life expectancy wouldn't be worth a lifetime of bland food and obsessive label-reading. If it reduces blood pressure by \(20mm\) with a confidence interval of \(\pm 5mm\), it might be worth it. So you should estimate the effect size (the difference in blood pressure between the diets) and the confidence interval on the difference.

In the third experiment, you are going to put magnetic hats on guinea pigs and see if their blood pressure goes down (relative to guinea pigs wearing the kind of non-magnetic hats that guinea pigs usually wear). This is a really goofy experiment, and you know that it is very unlikely that the magnets will have any effect (it's not impossible—magnets affect the sense of direction of homing pigeons, and maybe guinea pigs have something similar in their brains and maybe it will somehow affect their blood pressure—it just seems really unlikely). You might analyze your results using Bayesian statistics, which will require specifying in numerical terms just how unlikely you think it is that the magnetic hats will work. Or you might use frequentist statistics, but require a \(P\) value much, much lower than \(0.05\) to convince yourself that the effect is real.

• Picture of giant concrete chicken from Sue and Tony's Photo Site.
• Picture of guinea pigs wearing hats from all over the internet; if you know the original photographer, please let me know.