solving multi step equations homework 3

Free Multi Step Equations Worksheets

Multi Step Equations Worksheet Library

Free solving multi step equations worksheets and answer keys.

Download Free PDF Multi-Step Equations Worksheets and Answer Keys

Welcome to the Mashup Math Multi Step Equations Worksheet Library , where you can download free PDF worksheets with a variety of practice problems.

Each solving multi step equations worksheet in the library below is available as a PDF file that is easy to download or print. Each practice worksheet includes a variety of practice problems and a complete answer key.

You can click on any of the blue text links below to preview, download, or print any of our free worksheets. The second section of this page features a short review of how to solve a variety of multi-step equations , similar to the practice problems on our solving multi step equations worksheets pdf library.

Each PDF worksheet shared in the library below is a sample from the Mashup Math Practice Worksheet Libraries available on our website, where you can access tons of free algebra practice worksheets. | Reference Guide: How to Download/Print

Two-Sided Equations

Click Image to Preview

Extended Practice (Beginner)

Extended Practice (Intermediate)

▶️ Solving Two-Step Algebraic Equations (A)

▶️ Solving Two-Step Algebraic Equations (B)

▶️ Solving Two-Step Algebraic Equations (C)

▶️ Solving Two-Step Equations Extended Practice (A)

▶️ Solving Two-Step Equations Extended Practice (B)

▶️ Solving 2-Sided Algebraic Equations (A)

▶️ Solving 2-Sided Algebraic Equations (B)

▶️ Solving 2-Sided Algebraic Equations (C)

▶️ Solving Multi-Step Equations (A)

▶️ Solving Multi-Step Equations (B)

▶️ Solving Multi-Step Equations (C)

▶️ Solving Multi-Step Equations Extended Practice (Beginner)

▶️ Solving Multi-Step Equations Extended Practice (Intermediate)

▶️ Solving Multi-Step Equations Extended Practice (Advanced)

🛑 Are You Looking for More FREE Math Worksheets with Answers?

Visit the Mashup Math K-12 Worksheets Library , where you can download hundreds of practice worksheets with complete answer keys for Grades K-12+.

Multi Step Equations Worksheet Review

Are you struggling to solve any of the practice problems on any multi step equations worksheet shared in our free library? If so, this section will give you a step-by-step review of how to solve many types of problems that you will see on our solving multi step equations worksheets pdf downloads.

When it comes to solving multi step algebraic equations, the number one goal is always to isolate the variable by itself on one side of the equation by using inverse operations to rearrange the equation.

Inverse operations refers to the fact that each of the four main math operations—addition, subtraction, multiplication, and division—has an inverse, or opposite operation. The inverse of addition is subtraction and the inverse of subtraction is addition. And, the inverse of multiplication is division and the inverse of division is multiplication. With this in mind, let’s work through some practice problem examples of how to solve a mult-step algebraic equation.

Solving Multi-Step Equations Example #1

Example: Solve for x: 3x + 4 = 13

Let’s start off with a very simple multi-step equation, where we have to solve for x.

As with solving any algebraic equation, the aim is to isolate the variable (which is x in this case). We can do that using inverse operations to rearrange the equation, 3x + 4 = 13, so that x is by itself on one side of the equals sign, as follows:

Step #1: Isolate the x-term

3x + 4 = 13

3x + 4 -4 = 13 -4

Completing step one required us to isolate the x term by moving the +4 to the right side of the equation by applying inverse operations (the opposite of adding 4 is subtracting 4). After completing the first step, we are left with a new simplified equation, 3x=9, that we can solve as follows:

Step #2: Solve for x

(3x) /3 = 9 /3

For the second step, we had to divide both sides of the equation by 3 to get x by itself, resulting in x=3.

Final Answer: x=3 is the solution to the two-step equation 3x + 4 = 13.

We can do a check to confirm that our answer is correct by taking x=3 and substituting it into the equation that we started with (3x+4=13 in this case) and seeing if the left-side of the equation and the right-side of the equation equal the same value. If they do, then you know that you have solved the problem correctly. If not, then it is likely the case that you made an error somewhere along the process of solving the equation, and you should go by and solve the problem again.

Example #1 Check:

3(3) +4 = 13

Since x=3 work out, we have successfully solved this algebraic equation! Figure 01 below illustrates how we solved Example #1 in two steps.

Figure 01: Multi Step Equations Worksheet Review: Example #1 Solved

Solving Two-Step Equations Example #2

Example: Solve for x: 7𝑥 + 9 = 4𝑥 + 24

For our second example, notice that there is an x-term on each side of the equals sign. Our goal, however, is isolate the x, and we can do that by first isolating the x-term as follows:

Step #1: Isolate the x-term part one

7𝑥 + 9 = 4𝑥 + 24

7x -4x + 9 = 4x -4x + 24

3x + 9 = 24

Now we have a new simplified equation, 3x +9 =24. Our next step is to completely isolate the x-term as follows:

Step #2: Isolate the x-term part two

3x + 9 -9 = 24 -9

Now we are left with 3x=15. The last step to solving this multi step equation is to get x by itself on the left-side of the equation. Since 3x means “3 times x,” we can use inverse operations (i.e. division is the inverse of multiplication) as follows:

(3x) /3 = 15 /3

Final Answer: x=5 is the solution to the multi-step equation 7𝑥 + 9 = 4𝑥 + 24

We can check our answer by taking x=5 and substituting them back into 7𝑥 + 9 = 4𝑥 + 24 as follows:

7(5) + 9 = 4(5) + 24

35 + 9 = 20 + 24

Since we ended up with 44 on each side of the equals sign, we can say that our answer checks out and this multi step equation has been successfully solved.

The image in Figure 02 shows the step-by-step process for solving this multi-step equation below.

Figure 02: Multi Step Equations Worksheet Review: Example #2 Solved

Get More Free Math Resources!

Sign up for our mailing list and get two free pdf workbooks!

• Multi-Step Equation

Browse by Topics

• Cursive Writing
• Phonics Worksheets
• Vowels Worksheets
• Consonants Worksheets
• Consonant Blends
• Digraphs and Trigraphs Worksheets
• R Controlled Vowels
• Syllables Worksheets
• Rhyming Words Worksheets
• Reading Comprehension
• Standard Charts
• Number Charts
• Number Names Charts
• Coloring Activity
• Connecting Dots
• Trace & Color
• Cartoon Coloring
• Matching Activity
• Christmas Worksheets
• New Year worksheets
• Columbus Day Worksheets
• Easter Worksheets
• Halloween Worksheets
• Martin Luther King Worksheets
• Memorial Day Worksheets
• Saint Patrick’s Day
• Labor Day Worksheets
• Thanksgiving Day Worksheets
• Valentine’s Day Worksheets
• Veteran’s Day Worksheets
• Addition Tables
• Vertical Number Addition
• Horizontal Number Addition
• Picture Addition
• Addition Activities
• 3 Addends Addition
• Subtraction Tables
• Vertical Number Subtraction
• Horizontal Number Subtraction
• Picture Subtraction
• Subtraction Activities
• Problems Ending with Zero
• Multiplication Tables
• Number Multiplication - Vertical
• Number Multiplication - Horizontal
• Picture Application
• Multiplication Activities
• Division Tables
• Number Division - Horizontal
• Long Division - without Reminder
• Long Division - with Reminder
• Division Activities
• Decimal Addition
• Decimal Subtraction
• Roman Numerals
• Skip Counting
• Odd & Even Numbers
• Cardinal & Ordinal Numbers
• Rounding Numbers
• Estimation of Numbers
• Estimation of Time & Money
• Counting & Cardinality
• Comparing Numbers
• Ordering Numbers
• Representing Fractions
• Types of Fractions
• Fraction Addition
• Fraction Subtraction
• Comparing and Ordering Fractions
• Multiplying and Dividing Fractions
• Prime & Composite Numbers
• Squares & Cubes
• Divisibility Rules
• Factors & Multiples
• Tally Marks
• Pictographs
• Mean Median Mode Range
• Order of Operations
• Scientific Notation
• Algebraic Expressions
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Graphing Lines
• Point Slope Form
• Two Point Form
• Two Intercept Form
• One Step Equation
• Two Step Equation
• Multi Step Equation
• Graphing Linear Equation
• Solving Quadratic Equation
• Roots of Quadratic Equation
• Identifying Functions
• Evaluating Functions
• Function Table
• Domain and Range
• Trigonometric Charts
• Identifying Polynomials
• Classifying Polynomials
• Adding Polynomials
• Subtracting Polynomials
• Multiplying Polynomials
• Dividing Polynomials
• Polynomials - Box Method
• Big Vs Small
• Heavy Vs Light
• Long Vs Short
• More Vs Less
• Tall Vs Short
• Measurement of Length
• Length - Unit Conversions
• Measurement of Weight
• Weight - Unit Conversions
• Measurement of Capacity
• Capacity - Unit Conversions
• Temperature
• Compose / Decompose Shapes
• Lines, Rays, Line Segments, Planes
• Area of Triangles
• Area of Circles
• Area of Squares
• Area of Rectangles
• Area of Quadrilaterals
• Perimeter of Triangles
• Perimeter of Squares
• Perimeter of Rectangles
• Perimeter of Quadrilaterals
• Naming Angles
• Types of Angles
• Measuring Angles
• Complement / Supplement Angles
• Pair of Angles
• Circumference of Circles
• Types of Triangles
• Pythagorean Theorem
• Median and Centroid of Triangles
• Triangle Inequality Theorem
• Angles in Triangles
• Identifying Rectangles
• Area of Square
• Perimeter of Square
• Parallelogram
• Midpoint Formula
• Identifying Quadrilateral
• Area of Quadrilateral
• Perimeter of Quadrilateral
• Distance Formula
• Addition Word problems
• Money Word problems
• Time Word problems
• Lines / Rays Word problems

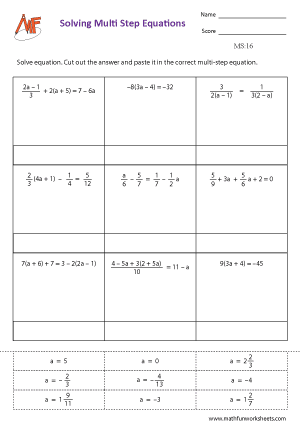
Multi-Step Equation Worksheets

This web page contains multi-step equation worksheets with different types of solved problems. Students from Grade 7 use these worksheets for practice. Solving equations with integers, fractions, decimals, matching, and cut-paste activities are also included here. After two-step equation worksheets, these worksheets are more popular for higher school studies.

Multi-Step Equation worksheets free download pdf

Solving equations - integers.

Solving Equations - Fractions

Solving Equations - Decimals

Solving Equations - Mixed

Cut Paste Activity

• Write for us
• Privacy Policy

Kindergarten Workbooks

• Alphabet Workbooks
• Numbers Workbooks
• Addition / Subtraction Workbooks
• Measurement Workbooks
• Geometry Workbooks

Grade 1 Workbooks

• Numbers and Placevalue Workbooks
• Addition and Subtraction Workbooks

Grade 2 Workbooks

• Operations and Algebraic thinking Workbooks
• Numbers and Operations Workbooks

Grade 3 Workbooks

• Operations and Algebraic Thinking
• Number and Operations in Base 10

Adobe Reader is required to download all the pdf files. If adobe reader is not installed in your computer, you may download it here for free: Adobe Reader Download.

Copyright © 2024. Math Fun Worksheets. All reserved!

Join the Math Fun Family! 🎉

Unlock unlimited access to our math worksheets sign up for free and enjoy endless learning opportunities., subscribe to view our website ad-free and keep the fun going.

Download Limit Reached

You have reached the maximum limit of 5 worksheets Downloads.

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Into Math Grade 8 Module 3 Lesson 1 Answer Key Solve Multi-step Linear Equations

We included H MH Into Math Grade 8 Answer Key PDF Module 3 Lesson 1 Solve Multi-step Linear Equations to make students experts in learning maths.

HMH Into Math Grade 8 Module 3 Lesson 1 Answer Key Solve Multi-step Linear Equations

I Can solve linear equations with integer and rational number coefficients.

శ్రీ వేంకటేశ ప్రపత్తిః

Turn and Talk Is there another equation that will solve the same problem? Explain.

Build Understanding

This is an example of a linear equation with only one solution.

Turn and Talk Which equation did you prefer to work with? Why?

Step It Out

A. Look at the decimals in the equation and think about how you could rewrite the equation with integer coefficients. What is the least power of 10 you could multiply each term by to eliminate all the decimals? ___________________ Answer: simplification: Multiply both sides by 100 1.2n *100 – 1.5 * 100 = 0.45n *100 120n – 150 = 45n B. Multiply each term of the original equation to eliminate all the decimals. Solve the equation. 1.2n – 1.5 = 0.45n ___ (1.2n) — ___ (1.5) = ___ (0.45n) ___ n – ___ = ___n ___n = ____ n = ____ Answer: simplification: Multiply both sides by 100 1.2n *100 – 1.5 * 100 = 0.45n *100 120n – 150 = 45n add 150 to both sides 120n – 150 + 150 = 45n + 150 120n = 45n + 150 120n – 45n = 150 75n = 150 n = 150/75 n = 2 C. Do you get the same solution? ___________________ Answer: Yes, both are equal. D. Which equation was easier to solve? Why? ___________________ Answer: The equation that is not having decimals because without decimals we can easily simplify the equation.

Turn and Talk How is solving an equation that involves fractions similar to solving an equation with decimals? What methods can you use to solve each Answer: Simplify both sides of the equation by combining like terms. If there are fractions, multiply both sides of the equation by the LCD (Least common denominator) of all the fractions. If there are decimals, multiply both sides of the equation by the lowest power of 10 to convert them into whole numbers.

B. Write the original equation, eliminate the fractions, and solve. \(\frac{1}{4}\)(p – 8) = 10 4[\(\frac{1}{4}\)(p – 8)] = 4(10) p – ___ = ___ P = ___ Answer: The above-given equation: 1/4(p – 8) = 10 to eliminate the factors, we need to multiply by 4 both sides (4) (1/4)[p- 8] = 10 * 4 p – 8 = 40 p = 40+ 8 p = 48

4. Solve the equation 4(2.5x + 2) – x = 26.9. A. Use the Distributive Property to write an equivalent equation. __________________ Distributive law: a(b + c) = ab + ac Answer: The given equation: 4(2.5x + 2) – x = 26.9. (4 * 2.5x + 4 * 2) – x = 26.9 10x + 8 – x = 26.9 B. Combine like terms, terms that have the same variable raised to the same exponent, and solve. __________________ Answer: continuing the part (A) combine like terms: 9x + 8 =26.9 9x = 26.9 – 8 9x = 18.9 x = 18.9/9 x = 2.1

Check Understanding

Question 2. Solve the equation. Check your solution. \(\frac{1}{5}\)(n – 10) = 6 – 3\(\frac{1}{2}\) Answer: The given equation: 1/5(n – 10) = 6 – 3 1/2 convert mixed numbers to improper fractions 3 1/2 = 7/2 1/5(n – 10) = 6 – 7/2 1/5n – 1/5 * 10 = 12 – 7/2 1/5 n – 2 = 5/2 1/5 n = 5/2 + 2 1/5 n = 9/2 multiply both sides by n 5 * 1/5 n = 5 * 9/2 n = 45/2 n = 22.5

On Your Own

Question 7. What is a first step to solve the equation 0.3n – 15 = 0.2n – 5? ______________ Answer: The above-given equation: 0.3n – 15 = 0.2n – 5 Multiply both sides by 10. 0.3n * 10 – 15 * 10 = 0.2n * 10 – 5 * 10 3n – 150 = 2n – 50 3n – 2n = -50 + 150 n = 100

Solve each equation. Check your solution.

Question 8. 3(x – 2) + 6 = 5(x + 4) ______________ Answer: The above-given equation: 3(x – 2) + 6 = 5(x + 4) Simplification: apply the distributive property. 3x – 6 + 6 = 5x + 20 3x = 5x + 20 subtract 5x from both sides 3x – 5x = 5x + 20 – 5x -2x = 20 x = -10

Question 9. 2.2(4p + 2) = 13.2 ______________ Answer: The above-given equation: 2.2(4p + 2) = 13.2 simplification: multiply both sides by 10 2.2(4p + 2) * 10 = 13.2 * 10 22(4p + 2) = 132 divide both sides by 22 22(4p + 2)/22 = 132/22 4p + 2 = 6 4p = 6 – 2 4p = 4 p = 1

Question 11. 2(11t + 1.5t) = 12 – 5t ______________ Answer: The above-given equation: 2(11t + 1.5t) = 12 – 5t Simplification: add similar elements 2(12.5t) = 12 – 5t 25t = 12 – 5t add 5t to the both sides 25t + 5t = 12 – 5t + 5t 30t = 12 t = 12/30 t =2/5 t = 0.4

Question 12. \(\frac{7}{8}\)m – \(\frac{1}{2}\) = \(\frac{3}{16}\)m + 5 Answer: The above-given equation: 7/8 m – 1/2 = 3/16m + 5 simplification: get all like terms into one side 7/8 m – 3/16 m = 5 + 1/2 7/8 m – 3/16 m = 10 + 1/2 7/8 m – 3/16 m = 11/2 11/16 m = 11/2 multiply both sides by 16 16 * 11/16 m = 11/2 * 16 11m = 88 m= 88/11 m = 8

Question 13. 9(n + 1) = 2(n – 1) Answer: The above-givene equation: 9(n + 1) = 2(n – 1) simplification: apply the distributive property 9n + 9 = 2n – 2 subtract 2n from both sides 9n + 9- 2n = 2n – 2 – 2n 7n + 9 = -2 7n = -2 – 9 7n = -11 n = -11/7

Question 14. \(\frac{4}{5}\)x – 3 = \(\frac{3}{10}\)x + 7 Answer: The above-given equation: 4/5 x – 3 = 3/10 x + 7 add 3 to the both sides 4/5 x – 3 + 3 = 3/10 x + 7 + 3 4/5 x = 3/10 x + 10 subtract 3/10 x from both sides 4/5 x – 3/10 x = 3/10 x + 10 – 3/10 x x(4/5 – 3/10) = 10 x(8 – 3/10) = 10 x(5/10) = 10 x(1/2) = 10 1/2 x = 10 x = 20

Question 15. -4(-5 – b) = \(\frac{1}{3}\)(b + 16) Answer: The above-given equation: -4(-5 – b) = 1/3(b + 16) apply distributive property 20 + 4b = 1/3b + 16/3 subtract 20 from both sides 20 + 4b – 20 = 1/3b + 16/3 – 20 4b = 1/3b + (16 – 60/3) 4b = 1/3b – 44/3 subtract 1/3b from both sides 4b – 1/3b = 1/3b – 44/3 – 1/3b b(4 – 1/3) = -44/3 b(12 – 1/3) = -44/3 b(11/3) = -44/3 11/3b = -44/3 b = -44/11 b = -4

Question 16. 3.6w = 2(0.8w + 12) Answer: The above-given equation: 3.6w = 2(0.8w + 12) apply distributive property 3.6w = 2 * 0.8w + 12 * 2 3.6w = 1.6w + 24 3.6w – 1.6w = 24 2w = 24 w = 12

I’m in a Learning Mindset!

How is the first step in solving a multi-step linear equation different from the first step in solving a multi-step word problem? Answer: The main goal in solving multi-step equations, just like in one-step and two-step equations, is to isolate the unknown variable on one side of the equation while keeping the constant or number on the opposite side. – Get rid of any grouping symbols such as square brackets, parentheses, etc, by applying the Distributive Property of Multiplication over Addition. – Simplify both sides of the equation, if possible, by combining like terms. – Decide where you want to keep the variable because that will help you decide where to place the constant. – Eliminate numbers or variables by applying opposite operations: addition and subtraction are opposite operations as in the case of multiplication and division.

Lesson 3.1 More Practice/Homework

Solve Multi-step Linear Equations

B. 21 = -2p – 5 __________ Answer: The above-given equation: 21 = -2p – 5 21 + 2p = -5 2p = -5 – 21 2p = -26 p = -26/2 p = -13

Question 3. Reason What step would you perform first to solve the following equation? Explain your reasoning. \(\frac{1}{4}\)(12 – 8x) = \(\frac{2}{3}\)(6x) Answer: The above-given equation: 1/4(12 – 8x) = 2/3 (6x) Multiply fractions: a(b/c) = a . b/c 1* (12 – 8x)/4 = 2/3 (6x) 12 – 8x/4 = 4x 3 – 2x = 4x 3 = 4x + 2x 3 = 6x switching the sides 6x = 3 x = 1/2 x = 0.5

Question 4. Heather has a family phone plan. The monthly payment for the family plan includes a $70 charge for unlimited talk and text, a $20 line fee per phone, and a $22.91 equipment fee for each phone. Their total monthly bill is $241.64. Write and solve an equation to find how many phones are on the plan. Answer: The number of phones = f The equation would be: f($70 + $20 + $22.91) = $241.64 f(112.91) = 241.64 f = 241.64/112.91 f = 2.14 approximately 2 phones. Therefore, there are 2 phones are on the plan.

Question 5. a + 3(a – 1) = 3(2 + 1) Answer: The above-given equation: a + 3(a – 1) = 3(2 + 1) simplification: a + 3a – 3 = 3(3) a + 3a – 3 = 9 a + 3a = 9 + 3 4a = 12 a = 12/4 a = 3

Question 6. 5y – 3(2 – y) = 10 Answer: The above-given equation: 5y – 3(2 – y) = 10 simplification: 5y – 6 + 3y = 10 8y – 6 = 10 8y = 10 + 6 8y = 16 y = 16/8 y = 2

Question 7. 1.2x – 2 = 7 + 0.9x Answer: The above-given equation: 1.2x – 2 = 7 + 0.9x multiply both sides by 10 1.2x * 10 – 2 * 10 = 7 * 10 + 0.9x * 10 12x – 20 = 70 + 9x get all like terms into one side 12x – 9x = 70 + 20 3x = 90 x = 90/3 x = 30

Question 8. -k + 4(k + 1) = 2k Answer: The above-given equation: -k + 4(k + 1) = 2k simplification: -k + 4k + 4 = 2k 3k + 4 = 2k get like terms on one side 3k – 2k = 4 k = 4

Question 9. 4(\(\frac{x}{6}\) + 5) = 2x + 10 Answer: The above-givne equation: 4(x/6) + 5 = 2x + 10 4x/6 + 5 = 2x + 10 get like on one side 2/3x – 2x = 10 -5 2x – 6x/3 = 5 -4x/3 = 5 -4x = 15 x = -15/4

Question 10. 3w + \(\frac{w}{2}\) + 1 = 10 – w Answer: The above-given equation: 3w + w/2 + 1 = 10 – w subtract 1 from both sides 3w + w/2 + 1 – 1 = 10 – w – 1 3w + w/2 = 9 – w multiply both sides by 2 3w * 2 + w/2 * 2 = 18 – w2 6w + w = 18 – w2 7w = 18 – w2 add w2 to both sides 7w + w2 = 18 – w2 + w2 9w = 18 w = 2

Question 11. Which could be the first step in solving the equation 0.05x + 3 — 0.02x = 4? A. Add 3 to each side of the equation. B. Divide each side of the equation by 100. C. Multiply each side of the equation by 100. D. Subtract 0.02x from each side of the equation. Answer: Option C is correct. The above-given equation; 0.05x + 3 – 0.02x = 4 0.03x + 3 = 4 Multiply both sides by 100 3x + 300 = 400 3x = 100 x = 33.333

Question 12. Solve the equation. Check your solution. \(\frac{3}{2}\)(x + 6) = 16 + \(\frac{1}{2}\)(x – 24) x = ___ Answer: The above-given equation: 3/2(x + 6) = 16 +1/2(x – 24) apply distributive property 3/2 x + 3/2 * 6 = 16 + 1/2 x – 1/2 * 24 3/2 x = 1/2 x – 20 subtract 1/2 x from both sides 3/2 x – 1/2 x = 1/2 x – 20 – 1/2 x x = -20

Question 13. Laurie earns $7.50 per hour at the fruit stand plus an extra $2.00 per hour on Sundays. One week in August, she worked on Sunday, Monday, and Wednesday. She worked the same number of hours on Monday and on Wednesday. On Sunday she worked 4 hours. If she earned a total of $83.00 for the week, how many hours did Laurie work on Monday? Write and solve an equation. Answer: The equation would be: we don’t know the number of hours so assume it as ‘h’ on Sundays, he works 4 hours and he gets $2 extra. In a week, he works for three days 7.50 + 2 = 9.50 In the question asked only for Monday hours 2(7.50h) + 9.50(4) = 83 14.50h + 38 = 83 14.50h = 83 – 38 14.50h = 45 h = 45/14.50 h = 3.1 (approximately 3 hours)

Question 14. Which equation has the solution x = 8? A. x + 2x – 4 = \(\frac{1}{4}\)(3x + 4) B. x + \(\frac{1}{2}\)(x + 8) = 4(1 + 3) C. 2(x – 4) = \(\frac{1}{4}\)(1 + 3) + x D. x + 4(1 + 3) = \(\frac{1}{2}\)(2x + 4) Answer: Option B is correct solve all the equations x + 1/2(x + 8) = 4(1 +3) x + 1/2 x + 1/2 . 8 = 16 x + 1/2 x + 4 = 16 x + 1/2 x = 16 – 4 x(1 + 1/2) = 12 x(3/2) = 12 3x/2 = 12 3x = 24 x = 8

Question 15. Each year Rolando saves 8% of his income. This year he saved $3000; his salary was $2000 less than the previous year. What was his salary in the previous year? Write and solve an equation. Answer: The previous income = N The income he saves each year = 8% of N In the present year, he saved = $3000 The salary = N – 2000 The equation would be: 8% (N – 2000) = 3000 8/100(N – 2000) = 3000 N- 2000 = 3000 x 100/8 N – 2000 = 37500 N = 37500 + 2000 N = 39500. Therefore, the previous salary is 39500.

Spiral Review

Question 16. Triangle ABC is dilated by a scale factor of 1.5 to form Triangle DEF. Are Triangles ABC and DEF congruent? Why or why not? Answer: Congruent means when they are the same shape and same size. If triangle ABC is dilated to form triangle DEF, that means that they will have the same shape and the same size. So yes Triangles ABC and DEF will be congruent to one another because they will be the same shape, and they will have the same size as well.

Question 17. A triangle has angles measuring 45°, 55°, and 80°. It is dilated by a scale factor of 2. What are the angle measures of the dilated image? Answer: Dilations preserve angle measures, regardless of the scale factor. Therefore, the angle measures of the image will be the same as that of the pre-image, so our answer is still 4545 °, 5555 °, and 8080 °.

POWERGRID Pivot Point Calculator

Leave a Comment Cancel Reply

You must be logged in to post a comment.