assignment on matrices class 12

Search This Blog

Featured posts, maths through stories | 17 camels & 3 sons, maths assignment class 12 chapter 3 | matrices, mathematics assignment class 12 , chapter 3 | matrices  .

Mathematics assignment for class XII chapter 3, Extra questions with answer key on chapter 3 matrices strictly according to the CBSE syllabus and very useful for examinations.

Mathematics Assignment On Matrices Class XII Chapter 3 

Find a matrix X such that 2A + B + X = 0, where

Ans:  K = 1

Ans: x = 5, y = 3

If B is a skew symmetric matrix, write whether the matrix (ABA') is symmetric or skew symmetric matrix

Ans: Skew symmetric matrix

Show that matrix B'AB is symmetric or skew symmetric according as A is symmetric or skew symmetric matrix.

Ans:  x = π / 3

and hence find a matrix X such that A 2  – 5A + 4I + X = 0

Solution Hint

Post a Comment

Breaking news, popular post on this blog, theorems on quadrilaterals ch-8 class-ix.

Lesson Plan Math Class 8 | Direct and Inverse Variation CH-4

Lesson Plan Maths Class 10 | For Mathematics Teacher

• Assignment 10 15
• Assignment 11 13
• Assignment 12 16
• Assignment 8 8
• Assignment 9 5
• Lesson plan 10 15
• Lesson Plan 12 14
• Lesson Plan 8 10
• Maths 10 20
• Maths 11 22
• Maths 12 18
• Story Telling 1

SUBSCRIBE FOR NEW POSTS

Get new posts by email:.

• You don't have any recent items yet.
• You don't have any courses yet.
• Add Courses
• You don't have any books yet.
• You don't have any Studylists yet.

CBSE Worksheets for Class 12 Maths Matrices Assignment

• Multiple Choice

Course : Mathematics (MATHS02)

University : university of rajasthan.

• More from: Mathematics MATHS02 University of Rajasthan 67   documents Go to course

Recommended for you

Students also viewed.

• Problems&Solutions - problem and solutions
• Cma+Audit-2016 +v-2 - efbwefvbwe
• Theatre - Britannica Online Encyclopedia 1
• CBSE Sample Paper Class 7 Maths SA2 Set 1
• Wolfe's & Beal's method
• ME010201 Advanced Abstract Algebra

Related documents

• Jam2024 IB - It is useful for iit jam
• Leec101 - Hello
• Delhi excise policy case 1264313 e92
• CA Intermediate Law Question Paper NOV. 2023
• CA Intermediate Accounts Question Paper Nov. 2023
• Paper 6 Set1 - kfbefblkw

CBSE NCERT Solutions

NCERT and CBSE Solutions for free

Class 12 Mathematics Matrices and Determinants Assignments

We have provided below free printable Class 12 Mathematics Matrices and Determinants Assignments for Download in PDF. The Assignments have been designed based on the latest NCERT Book for Class 12 Mathematics Matrices and Determinants . These Assignments for Grade 12 Mathematics Matrices and Determinants cover all important topics which can come in your standard 12 tests and examinations. Free printable Assignments for CBSE Class 12 Mathematics Matrices and Determinants , school and class assignments, and practice test papers have been designed by our highly experienced class 12 faculty. You can free download CBSE NCERT printable Assignments for Mathematics Matrices and Determinants Class 12 with solutions and answers. All Assignments and test sheets have been prepared by expert teachers as per the latest Syllabus in Mathematics Matrices and Determinants Class 12. Students can click on the links below and download all Pdf Assignments for Mathematics Matrices and Determinants class 12 for free. All latest Kendriya Vidyalaya Class 12 Mathematics Matrices and Determinants Assignments with Answers and test papers are given below.

Mathematics Matrices and Determinants Class 12 Assignments Pdf Download

We have provided below the biggest collection of free CBSE NCERT KVS Assignments for Class 12 Mathematics Matrices and Determinants . Students and teachers can download and save all free Mathematics Matrices and Determinants assignments in Pdf for grade 12th. Our expert faculty have covered Class 12 important questions and answers for Mathematics Matrices and Determinants as per the latest syllabus for the current academic year. All test papers and question banks for Class 12 Mathematics Matrices and Determinants and CBSE Assignments for Mathematics Matrices and Determinants Class 12 will be really helpful for standard 12th students to prepare for the class tests and school examinations. Class 12th students can easily free download in Pdf all printable practice worksheets given below.

Topicwise Assignments for Class 12 Mathematics Matrices and Determinants Download in Pdf

Advantages of Class 12 Mathematics Matrices and Determinants Assignments

• As we have the best and largest collection of Mathematics Matrices and Determinants assignments for Grade 12, you will be able to easily get full list of solved important questions which can come in your examinations.
• Students will be able to go through all important and critical topics given in your CBSE Mathematics Matrices and Determinants textbooks for Class 12 .
• All Mathematics Matrices and Determinants assignments for Class 12 have been designed with answers. Students should solve them yourself and then compare with the solutions provided by us.
• Class 12 Students studying in per CBSE, NCERT and KVS schools will be able to free download all Mathematics Matrices and Determinants chapter wise worksheets and assignments for free in Pdf
• Class 12 Mathematics Matrices and Determinants question bank will help to improve subject understanding which will help to get better rank in exams

Frequently Asked Questions by Class 12 Mathematics Matrices and Determinants students

At https://www.cbsencertsolutions.com, we have provided the biggest database of free assignments for Mathematics Matrices and Determinants Class 12 which you can download in Pdf

We provide here Standard 12 Mathematics Matrices and Determinants chapter-wise assignments which can be easily downloaded in Pdf format for free.

You can click on the links above and get assignments for Mathematics Matrices and Determinants in Grade 12, all topic-wise question banks with solutions have been provided here. You can click on the links to download in Pdf.

We have provided here topic-wise Mathematics Matrices and Determinants Grade 12 question banks, revision notes and questions for all difficult topics, and other study material.

We have provided the best collection of question bank and practice tests for Class 12 for all subjects. You can download them all and use them offline without the internet.

Related Posts

Class 12 Economics Assignments

Class 12 Entrepreneurship Assignments

Class 12 Mathematics Relations and Functions Assignments

CLASS XII RELATIONS AND FUNCTIONS

CLASS XII INVERSE TRIGONOMETRY

CLASS XII MATRICES

CLASS XII DETERMINANTS

CLASS XII CONTINUITY & DIFFERENTIABILITY

CLASS XII APPLICATION OF DERIVATIVES

CLASS XII INTEGRATION

CLASS XII APPLICATIONS OF INTEGRATION

CLASS XII DIFFERENTIAL EQUATIONS

CLASS XII VECTOR ALGEBRA

CLASS XII THREE DIMENTIONAL GEOMETRY

CLASS XII LINEAR PROGRAMMING PROBLEMS

CLASS XII PROBABILITY

CLASS XII ASSIGNMENTS (Old)

Ch 1 Relation and Function

Ch 2 Inverse Trigonometry

Ch 3 Matrices

Ch 4 Determinants

Ch 5 Continuity and Differentiability

Ch 6 Application of Derivatives

Ch 7 Integrals

Ch 8 Applications of Integrals

Ch 9 Differential Equations

Ch 10 Vector Algebra

Ch 11 3D Geometry

Ch 13 Probability

Formula List (Book 1 Based)

Formula List (Book 2 Based)

• Math Article

Matrices For Class 12

Matrices Class 12 Notes

Matrix is one of the important concepts of Mathematics and one of the most powerful tools, which has various applications such as in solving linear equations, budgeting, sales projection, cost estimation, etc. Matrices for class 12 covers the important concepts in matrices, such as types, order, matrix elementary transformation operations and so on. Students can get a detailed explanation of matrix concepts here. Matrices for class 12 helps the students with their higher studies, as it covers all the basic topics. Go through the notes on class 12 matrices to score good marks in the examinations.

Matrices for Class 12 Topics

The topics covered in matrices for class 12 include the following topics:

• Introduction
• Types of Matrices  
• Operations on Matrices 
• Transpose of a Matrix 

Symmetric and Skew Symmetric Matrices

Elementary operation (transformation) of a matrix .

• Invertible Matrices

Matrices Definition

A matrix is a function that consists of an ordered rectangular array of numbers. The numbers in the array are called the entities or the elements of the matrix. The horizontal array of elements in the matrix is called rows, and the vertical array of elements are called the columns. If a matrix has m rows and n columns, then it is known as the matrix of order m x n.

Learn: Matrices

To know, how to determine the order of a matrix, visit here .

Types of Matrices

Depending upon the order and elements, matrices are classified as:

• Column matrix
• Square matrix
• Diagonal matrix
• Scalar matrix
• Identity matrix
• Zero matrix

Let’s understand the definition of all these types of matrices along with examples here.

Equality of Matrices

Two matrices are said to be equal if-

(i) The order of both the matrices is the same

(ii) Each element of one matrix is equal to the corresponding element of the other matrix

Operations on Matrices

In Chapter 3 of Class 12 Matrices, certain operations on matrices are discussed, namely, the addition of matrices, multiplication of a matrix by a scalar, difference and multiplication of matrices.

Also, Check:

• Addition of Matrices
• Subtraction of matrices
• Matrix multiplication

Transpose of a Matrix

 If A = [a ij ] be an m × n matrix, then the matrix obtained by interchanging the rows and columns of A is called the transpose of A and is denoted by A′ or (A T ). 

In other words, if A = [a ij ] m × n , then A′ = [a ji ] n × m . 

\(\begin{array}{l}Matrix ,\ A = \begin{bmatrix} 2 &1&3\\ -4&0&5\\ \end{bmatrix}\end{array} \)

To learn more about transpose of a matrix , visit here.

 A square matrix A = [a ij ] is said to be symmetric if the transpose of A is equal to A, that is, [a ij ] = [a ji ] for all possible values of i and j.

A square matrix A = [a ij ] is a skew-symmetric matrix if A′ = – A, that is a ji = – a ij for all possible values of i and j. Also, if we substitute i = j, we have a ii = – a ii and thus, 2a ii = 0 or a ii = 0 for all i’s. Therefore, all the diagonal elements of a skew-symmetric matrix are zero.

To understand the symmetric and skew-symmetric matrix in detail, visit here .

There are six operations (transformations) on a matrix, three of which are due to rows, and three are due to columns, known as elementary operations or transformations.

• The interchange of any two rows or two columns.
• The multiplication of the elements of any row or column by a non zero number.
• The addition to the elements of any row or column, the corresponding elements of any other row or column are multiplied by any non zero number.

Learn more about the elementary operations of the matrix here.

Invertible Matrices 

Suppose a square matrix A of order m, and if there exists another square matrix B of the same order m, such that AB = BA = I, then B is called the inverse matrix of A, and it is denoted by A -1 . Also, matrix A is said to be an invertible matrix here.

To get complete information about invertible matrices, visit here .

Video Lesson on Matrices and Determinants Class 12

Matrices for Class 12 Examples

Example 1: 

It is given that, the two matrices are equal. Therefore, the corresponding elements present in matrices should be equal to each other. By comparing the corresponding elements in the matrices, we get:

2y-7 = 3y-2

⇒3y-2y =-7+2

⇒2b-b = -3-4

Therefore, the values of the variables are:

\(\begin{array}{l}AB=\begin{bmatrix} 1\\3\\-6 \end{bmatrix}\begin{bmatrix} -2&4&5 \end{bmatrix}\\=\begin{bmatrix} -2&4&5\\ -6&12&15\\ 12&-24&-30 \end{bmatrix}\end{array} \)

Now, we need to calculate the transpose of AB.

\(\begin{array}{l}(AB)^T=\begin{bmatrix} -2&-6&12\\ 4&12&-24\\ 5&15&-30 \end{bmatrix}\end{array} \)

\(\begin{array}{l}A^T=\begin{bmatrix} 1&3&-6 \end{bmatrix}\end{array} \)

\(\begin{array}{l}B^T=\begin{bmatrix} -2\\ 4\\5 \end{bmatrix}\end{array} \)

\(\begin{array}{l}B^TA^T=\begin{bmatrix} -2\\ 4\\5 \end{bmatrix}\begin{bmatrix} 1&3&-6 \end{bmatrix}=\begin{bmatrix} -2&-6&12\\ 4&12&-24\\ 5&15&-30 \end{bmatrix}\end{array} \)

Therefore, (AB) T = B T A T .

Hence verified.

To learn more on matrix-related concepts, register with BYJU’S – The Learning App and download the app today!

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Thank you so much. This is very helpful for me in this pandemic situation.

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Class 6 Maths
• Class 6 Science
• Class 6 Social Science
• Class 6 English
• Class 7 Maths
• Class 7 Science
• Class 7 Social Science
• Class 7 English
• Class 8 Maths
• Class 8 Science
• Class 8 Social Science
• Class 8 English
• Class 9 Maths
• Class 9 Science
• Class 9 Social Science
• Class 9 English
• Class 10 Maths
• Class 10 Science
• Class 10 Social Science
• Class 10 English
• Class 11 Maths
• Class 11 Computer Science (Python)
• Class 11 English
• Class 12 Maths
• Class 12 English
• Class 12 Economics
• Class 12 Accountancy
• Class 12 Physics
• Class 12 Chemistry
• Class 12 Biology
• Class 12 Computer Science (Python)
• Class 12 Physical Education
• GST and Accounting Course
• Excel Course
• Tally Course
• Finance and CMA Data Course
• Payroll Course

Interesting

• Learn English
• Learn Excel
• Learn Tally
• Learn GST (Goods and Services Tax)
• Learn Accounting and Finance
• GST Tax Invoice Format
• Accounts Tax Practical
• Tally Ledger List
• GSTR 2A - JSON to Excel

You are learning...

Chapter 3 Class 12 Matrices

Click on any of the links below to start learning from Teachoo ...

Learn Chapter 3 Matrices of Class 12 free with solutions of all NCERT Questions including Examples and Exercises.  

In this chapter, we learn

• What a matrix is , how we form it and what is its order
• Then we see different types of matrix like Square matrix, Zero matrix, Identity Matrix, Row Matrix, Column Matrix etc.
• If two matrices are equal , then how to find its elements
• How to add and subtract matrices ,
• And their Statement questions
• Then how to multiply the matrices , keeping in mind their order
• And its statement questions
• How to solve a x + y, or an x + y + z equation using matrices
• Then, finding an element when some equation is given
• Or, finding a whole matrix when some equation is given
• What is a Transpose of a Matrix , and its order
• Then, What are Symmetric and skew symmetric matrices ... and how to represent any matrix as a sum of symmetric and skew symmetric matrix
• Then, doing some proof questions using Transpose property - (AB)' = B'A'
• And finding Inverse of a matrix using elementary Transformation. Please check all of its questions. Specially the ones marked important
• And then, finally, there are some questions on proof using Mathematical Induction

Check out the chapter NCERT way, or the preferred ... concept wise way

Serial order wise

Concept wise.

What's in it?

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

NCERT Solutions for Class 12 Maths Chapter 3 Matrices

Class 12 Maths Chapter 3 NCERT Solutions Class 12 Math Exercise 3.1 in English Class 12 Math Exercise 3.2 in English Class 12 Math Exercise 3.3 in English Class 12 Math Exercise 3.4 in English 12th Maths Chapter 3 Misc. Exercise

Get here modified NCERT Solutions for Class 12 Maths Chapter 3 Matrices in English and Hindi Medium updated for academic session 2024-25. The question answers and solutions are revised according to new NCERT books published for 2024-25 board exams.

Class 12 Maths Chapter 3 Solutions in English Medium

• Class 12 Math Exercise 3.1 in English
• Class 12 Math Exercise 3.2 in English
• Class 12 Math Exercise 3.3 in English
• Class 12 Math Exercise 3.4 in English
• 12th Maths Chapter 3 Misc. Exercise

Class 12 Math Chapter 3 Solutions in Hindi Medium

• Class 12 Math Exercise 3.1 in Hindi
• Class 12 Math Exercise 3.2 in Hindi
• Class 12 Math Exercise 3.3 in Hindi
• Class 12 Math Exercise 3.4 in Hindi
• 12th Maths Chapter 3 Misc. Exercise in Hindi

Class 12 Maths Chapter 3 Solutions are useful for CBSE and UP Board students, they can download these plus two solutions in PDF format free otherwise use online these updated solutions for the new academic session 2024-25. In Uttar Pradesh now NCERT Textbooks are implemented for class 12, so students of 10+2 can use these UP Board Solution for Class 12 Maths Chapter 3. In every question of 12th Maths Chapter 3 Matrix, the explanation of each step is given. The step by step solutions for plus two Maths is given with video solution and text file format. Madhya Pradesh and Gujrat Board are also following Textbooks of NCERT. So, these solutions of 12th Maths Chapter 3, is important not only for CBSE or UP Board Students, but the other boards also who are using 12th NCERT Textbooks as current course books.

Download NCERT Solutions Class 12 Maths chapter 3 exercise 3.1, 3.2, 3.3, 3.4 and miscellaneous exercises in English and Hindi Medium for CBSE Board . UP Board Students are using the same NCERT Books, so they can also use these solutions as UP Board Solutions 12 Maths Chapter 3 for the academic session 2024-25. We have done everything perfectly to provide solutions of Class 12 Maths for CBSE and UP Board, if you feel some problem, inform us. We will definitely rectify.

Class 12 Maths Chapter 3 Study Material

• Class 12 Maths NCERT Book Chapter 3
• Download 12th Maths Revision Book Chapter 3
• Download 12th Maths Revision Book Answers
• Download Class 12 Maths Chapter 3 Assignment 1
• Download Class 12 Maths Chapter 3 Assignment 2
• Download Class 12 Maths Chapter 3 Assignment 2 Answers
• Download Class 12 Maths Chapter 3 Assignment 3
• Download Class 12 Maths Chapter 3 Assignment 4
• Class 12 Maths NCERT Solutions
• Class 12 all Subjects NCERT Solutions

The arrangement of real numbers in a rectangular array enclosed in brackets as [] or () is known as a Matrix (Matrices is plural of matrix). Matrix operations are used in electronic physics, computers, budgeting, cost estimation, analysis and experiments. They are also used in cryptography, modern psychology, genetics, industrial management etc. In general an m x n matrix is matrix having m rows and n columns. it can be written as follows:

• Order of a Matrix There may be any number of rows and any number of columns in a matrix. If there are m rows and n columns in matrix A, its order is m x n and it is read as an m x n matrix.
• Transpose of a Matrix The transpose of a given matrix A is formed by interchanging its rows and columns and is denoted by A’.
• Symmetric Matrix A square matrix A is said to be a symmetric matrix if A’ = A.
• Skew-Symmetric Matrix A square matrix A is said to be a skew symmetric if A’ = – A. all elements in the principal diagonal of a skew symmetric matrix are zeroes.
• Addition of Matrix If A and B are any two given matrices of the same order, then their sum is defined to be a matrix C whose respective elements are the sum of the corresponding elements of the matrices A and B and we write this as C = A + B.

Types of Matrices

• Row matrix: A row matrix has only one row but any number of columns.
• Column matrix: A column matrix has only one column but any number of rows.
• Square matrix: A square matrix has the number of column equal to the number of rows.
• Rectangular Matrix: A matrix is said to be a rectangular matrix if the number of rows is not equal to the number of columns.
• Diagonal matrix: If in a square matrix has all elements 0 except principal diagonal elements, it is called diagonal matrix.
• Scalar Matrix: A diagonal matrix is said to be a scalar matrix if all the elements in its principal diagonal are equal to some non-zero constant.
• Zero or Null matrix: If all elements of a matrix are zero, then the matrix is known as zero matrix and denoted by O.
• Unit or Identity matrix: If in a square matrix has all elements 0 and each diagonal elements are non-zero, it is called identity matrix and denoted by I.
• Equal Matrices: Two matrices are said to be equal if they are of the same order and if their corresponding elements are equal.

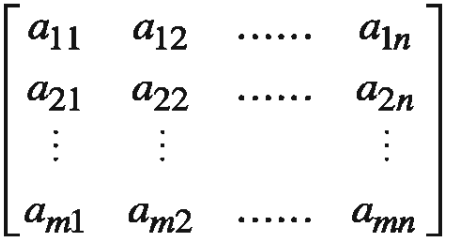
Properties of Matrices

• When a matrix is multiplied by a scalar, then each of its element is multiplied by the same scalar.
• If A and B are any two given matrices of the same order, then their sum is defined to be a matrix C whose respective elements are the sum of the corresponding elements of the matrices A and B and we write this as C = A + B.
• For any two matrices A and B of the same order, A + B = B + A. i.e. matrix addition is commutative.
• For any three matrices A, B and C of the same order, A + (B + C) = (A + B) + C i.e., matrix addition is associative.
• Additive identity is a zero matrix, which when added to a given matrix, gives the same given matrix, i.e., A + O = A = O + A.
• If A + B = O, then the matrix B is called the additive inverse of the matrix of A.
• If A and B are two matrices of order m x p and p x n respectively, then their product will be a matrix C of order m x n.

Invertible Matrix

A square matrix of order n is invertible if there exists a square matrix B of the same order such that AB = I = BA, Where I is identify matrix of order n. Theorems of invertible matrices

• Theorem 1: Every invertible matrix possesses a unique inverse.
• Theorem 2: A square matrix is invertible iff it is non-singular.

Historical Facts!

Matrix is a latin word. Originally matrices are used for solutions of simultaneous linear equations in Mathematics . An important Chinese Text between 300 BC and 200 AD, nine chapters of Mathematical Art(Chiu Chang Suan Shu), give the use of matrix methods to solve simultaneous equations. Carl Friedrich Gauss(1777 – 1855) also gave the method to solve simultaneous equations by matrix method.

What does chapter 3 of class 12th Maths explore about Matrix?

A matrix is an ordered rectangular array of numbers or functions. The numbers or functions are called the elements or the entries of the matrix. We denote matrices by capital letters. The following are some examples of matrices: – In the above examples, the horizontal lines of elements are said to constitute, rows of the matrix and the vertical lines of elements are said to constitute, columns of the matrix. Thus A has 3 rows and 2 columns and B has 3 rows and 3 columns.

What are the practical implimentations of matrices chapter 3 of 12th Maths in different fields?

The knowledge of matrices is necessary in various branches of mathematics. Matrices are one of the most powerful tools in mathematics. The evolution of the concept of matrices is the result of an attempt to obtain compact and simple methods of solving a system of linear equations. Matrix notation and operations are used in electronic spreadsheet programs for personal computer, which in turn is used in different areas of business and science like budgeting, sales projection, cost estimation, analyzing the results of an experiment, etc. Also, many physical operations such as magnification, rotation, and reflection through a plane can be represented mathematically by matrices. Matrices are also used in cryptography. This mathematical tool is not only used in certain branches of sciences but also in genetics, economics, sociology, modern psychology, and industrial management.

How many exercises are there in chapter 3 of class 12th Maths for 1st term exam?

There are 5 exercises in chapter 3 of class 12th Maths. The first exercise (Ex 3.1) has 15 sums (5 examples and 10 questions). The second exercise (Ex 3.2) contains 36 sums (14 examples and 22 questions). In the third exercise (Ex 3.3), there are 15 sums (3 examples and 12 questions). The fourth exercise has 21 sums (3 examples and 18 questions). There are 18 sums (3 examples and 15 questions) in the last (Miscellaneous) exercise.

Are there any theorems in chapter 3 of class 12th Maths?

Yes, there are four theorems in chapter 3 of class 12th Maths. All the theorems are nice, easy, and important. Proofs of these theorems are short and easy. Students can easily understand the theorems and proofs of these theorems.

« Inverse Trigonometric Functions

Determinants ».

Copyright 2024 by Tiwari Academy | A step towards Free Education

NCERT Solutions Class 12 Maths Chapter 3 Matrices

NCERT Solutions for Class 12 Maths Chapter 3 Matrices provide a detailed explanation of all the fundamental concepts covered under this topic. Matrices are an indispensable part of maths studies that simplifies work to a great extent. The topic of matrices finds its applications in various branches of mathematics. It is a simple method for solving linear equations. The applications of matrices are not only limited to representing the coefficients of linear equations; they are also used in electronic spreadsheets that are required in business and science. Moreover, the use of matrices is also prevalent in genetics, economics, sociology, modern psychology, and industrial management. Thus, it is crucial to attaining a deep knowledge of this topic and its applications.

NCERT Solutions Class 12 Maths Chapter 3, students will become acquainted with the fundamentals of matrix and matrix algebra. Some of the important topics explained in this chapter are based on understanding the representation of matrices, their orders, types, and algebra. With the regular practice of Class 12 Maths NCERT Solutions Chapter 3, students will quickly gain a deep understanding of this topic. To learn and practice with NCERT Solutions Chapter 3 Matrices, download the exercises provided in the links below.

• NCERT Solutions Class 12 Maths Chapter 3 Ex 3.1
• NCERT Solutions Class 12 Maths Chapter 3 Ex 3.2
• NCERT Solutions Class 12 Maths Chapter 3 Ex 3.3
• NCERT Solutions Class 12 Maths Chapter 3 Ex 3.4
• NCERT Solutions Class 12 Maths Chapter 3 Miscellaneous Exercise

NCERT Solutions for Class 12 Maths Chapter 3 PDF

A matrix is a rectangular arrangement of an array of numbers or functions. These numbers or functions are known as the elements of the matrix. NCERT Solutions for Class 12 Maths are meticulously formulated guides that promote the fundamental understanding of the representation of matrices along with their properties and their types. To practice with these solutions, click on the links of the pdf files given below.

☛ Download Class 12 Maths NCERT Solutions Chapter 3 Matrices

NCERT Class 12 Maths Chapter 3   Download PDF

NCERT Solutions for Class 12 Maths Chapter 3 Matrices

NCERT solutions Class 12 Maths Chapter 3 Matrices are highly competent guides that efficiently impart the complete knowledge of Matrices and their applications. These resources deliver deep conceptual knowledge of each concept to strengthen the students’ key skills. The interactive format of these solutions is pretty apt for in-depth study of all topics. To practice the exercise-wise NCERT Solutions Class 12 Maths Matrices, try the links given below.

• Class 12 Maths Chapter 3 Ex 3.1 - 10 Questions
• Class 12 Maths Chapter 3 Ex 3.2 - 22 Questions
• Class 12 Maths Chapter 3 Ex 3.3 - 12 Questions
• Class 12 Maths Chapter 3 Ex 3.4 - 18 Questions
• Class 12 Maths Chapter 3 Miscellaneous Ex - 15 Questions

☛ Download CBSE Class 12 Maths Chapter 3 NCERT Book

Topics Covered: The topics covered in NCERT Solutions Class 12 Maths Chapter 3 are an introduction to fundamentals of the matrix, order of a matrix , types of matrices , operations on matrices, transpose of a matrix , symmetric and skew-symmetric matrices , elementary operation of a matrix, and invertible matrices . The important subtopics included in this chapter are the properties of matrix operations and the transpose of a matrix.

Total Questions: Class 12 Maths Chapter 3 Matrices has 62 questions in 4 exercises along with 15 more provided in a miscellaneous exercise. Out of these 41 questions are short answer types, 11 multiple choice questions, and 25 long answer type questions.

List of Formulas in NCERT Solutions Class 12 Maths Chapter 3

A matrix is a rectangular array of numbers represented as rows and columns. Performing arithmetic operations on matrices requires a basic understanding of their types, rules, and properties. Thus, it is highly important to concentrate on the laws, and identities of matrices. NCERT Solutions Class 12 Maths Chapter 3 explains each of these concepts with the help of interactive illustrations. Some of the important terms and definitions elaborated in these NCERT Solutions for Class 12 Maths Chapter 3 are given below.

• Order of Matrix: The order of the matrix is defined as the product of the number of rows by the number of columns. A matrix with ‘m’ rows and ‘n’ columns is known as a matrix of order m × n. The numerical notation of a matrix A of order m x n is A = [a ij ] m × n
• Column Matrix: A matrix of order m x1 is known as a column matrix. The notation used to represent a column matrix is [a ij ] mx1 .
• Row Matrix: A matrix of order 1 x n is known as a row matrix. The notation used to represent a column matrix is [a ij ]
• Square Matrix: A matrix of order m × n matrix is a square matrix if m=n.
• Diagonal Matrix: A matrix M = [a ij ] m×m is called a diagonal matrix if a ij = 0, when i is not equal to j.
• Scalar Matrix: A matrix M = [a ij ]n×n is known as a scalar matrix if a ij =0 when i is not equal to j and a ij = k, when i is equal to j, where k is some constant.
• Identity Matrix: A matrix M = [a ij ] n×n is an identity matrix if a ij = 1, when i = j, a ij = 0, when i≠j.
• Zero Matrix: A matrix with all its elements as zero is called a zero matrix.
• Equal Matrices: Two matrices A and B are said to be equal if they have the same order and equal corresponding elements, i.e., the value of a ij = b ij for all i and j.
• Negative of a Matrix: The negative of a matrix is denoted by – A. It can be represented as -A = (-1) A

FAQs on NCERT Solutions for Class 12 Maths Chapter 3

What is the importance of ncert solutions for class 12 maths chapter 3 matrices.

NCERT Solutions for Class 12 Maths Chapter 3 Matrices are purposefully designed by subject experts to deliver a deep conceptual understanding of fundamentals. With the thorough practice of these solutions, students can perform strategic exam preparation. These well-framed solutions are apt for raising the math proficiency and confidence in students required to face various competitive exams. Practicing with these resources also promotes a sense of self-accomplishment.

What are the Important Topics Covered in NCERT Solutions Class 12 Maths Chapter 3?

Chapter 3 Matrices of class 12 Maths briefly defines all the important applications and uses of matrices in various subjects and disciplines. The important topics covered in the NCERT Solutions Class 12 Maths Chapter 3 are the order of a matrix, types of matrices, their mathematical operations, transpose of a matrix, symmetric matrices, skew-symmetric matrices, elementary operation, and invertible matrices. Solving the complete set of questions provided in these solutions will be quite helpful in improving the fundamental understanding of matrices. The prime objective of these solutions is to improve the learnability and math potential of kids to help them achieve their desired results.

Do I Need to Practice all Questions Provided in NCERT Solutions Class 12 Maths Matrices?

Practicing all the questions included in NCERT Solutions Class 12 Maths Matrices gives a step-by-step knowledge of each topic. Questions in these solutions are well-placed at a gradually increasing level to help students comfortably adjust to the rising complexity. Students can quickly grasp the core fundamentals of Matrices and their applications by solving and practicing these sums. Learning with these solutions is also beneficial in preparing for various competitive exams and higher-level studies.

How Many Questions are there in Class 12 Maths NCERT Solutions Chapter 3 Matrices?

NCERT Solutions Class 12 Maths Chapter 3 Matrices has 77 questions in 5 exercises. Practicing these questions ensures an accurate and clear understanding of this topic. Students can also plan systematic learning of these exercises and concepts based on Matrices. The lucid format of these solutions is efficient in acquiring a sound knowledge of the operations and types of Matrices.

What are the Important Formulas in NCERT Solutions Class 12 Maths Chapter 3?

NCERT Solutions Class 12 Maths Chapter 3 mainly focuses on the Matrices, their types, and properties. Some of the important concepts explained in these solutions are based on arithmetic operations and the properties of matrices. These topics are covered in detail with the help of examples and illustrations. These solutions are heavily focused on imparting a precise conceptual understanding of fundamentals.

Why Should I Practice NCERT Solutions for Class 12 Maths Chapter 3 Matrices?

NCERT Solutions for Class 12 Maths Chapter 3 Matrices is a competent learning resource that offers complete guidance and practice of core concepts for higher-level studies. These solutions cover the whole syllabus of CBSE Class 12 Maths Chapter 3 to provide comprehensive learning of all topics. The format of these solutions is pretty convenient to clear doubts and learn complex concepts. With the thorough practice of these resources, students can ensure good results in their annual maths exam.