ai websites for presentations

stop bullying

11 templates

44 templates

welcome back

90 templates

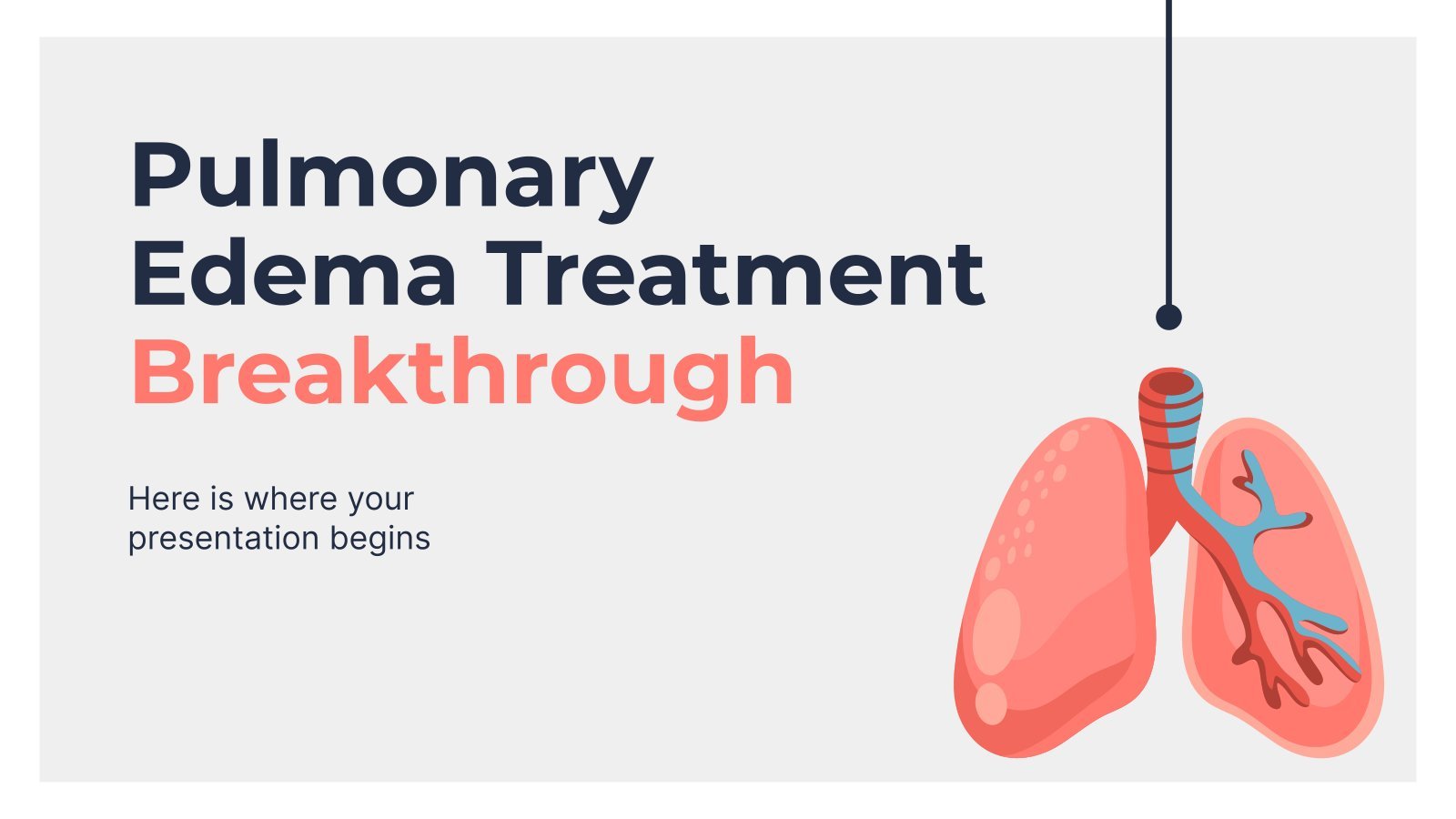
27 templates

business pitch

695 templates

Create your presentation Create personalized presentation content

Writing tone, number of slides, ai presentation maker.

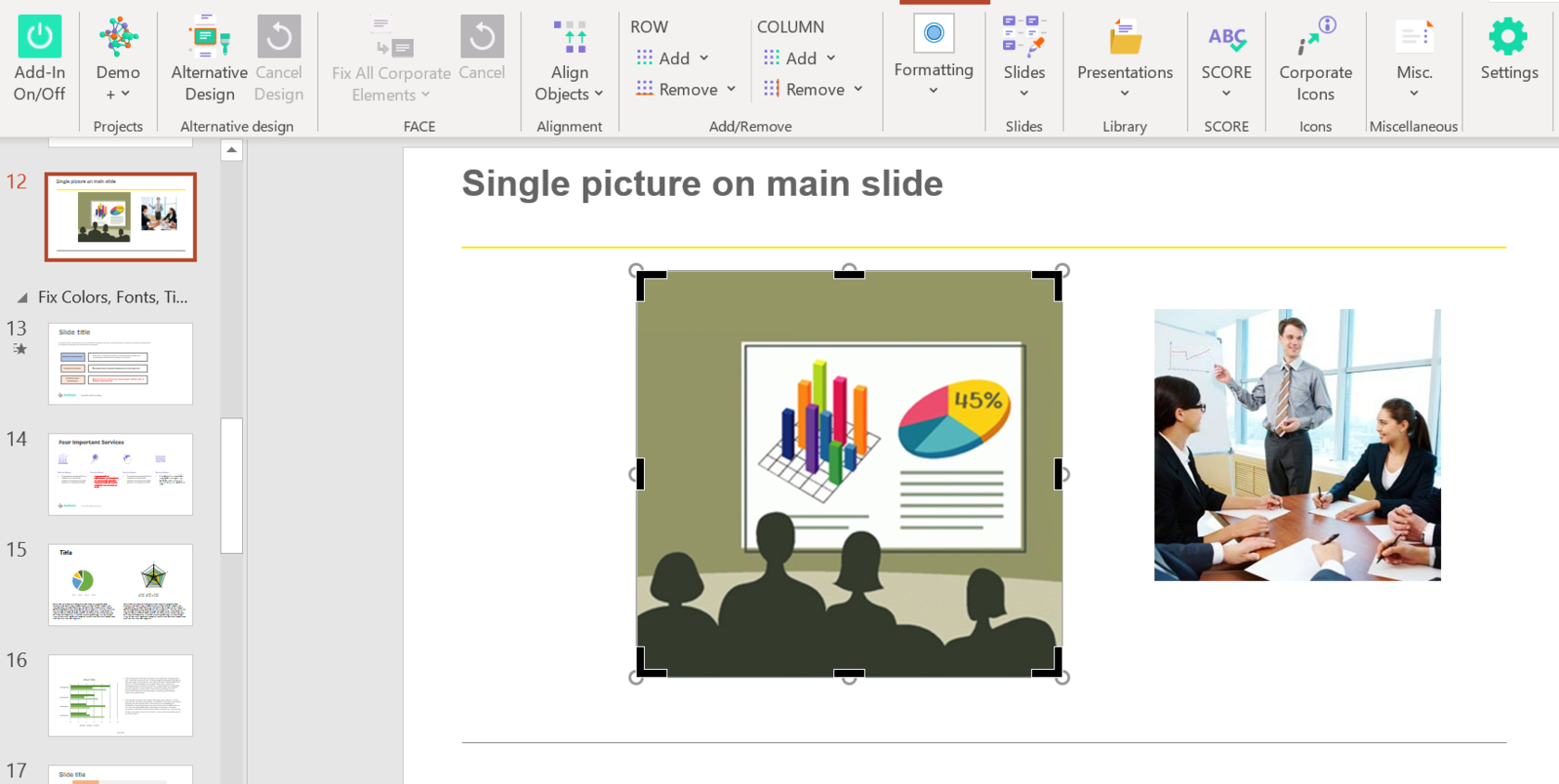
When lack of inspiration or time constraints are something you’re worried about, it’s a good idea to seek help. Slidesgo comes to the rescue with its latest functionality—the AI presentation maker! With a few clicks, you’ll have wonderful slideshows that suit your own needs . And it’s totally free!

Generate presentations in minutes

We humans make the world move, but we need to sleep, rest and so on. What if there were someone available 24/7 for you? It’s time to get out of your comfort zone and ask the AI presentation maker to give you a hand. The possibilities are endless : you choose the topic, the tone and the style, and the AI will do the rest. Now we’re talking!

Customize your AI-generated presentation online

Alright, your robotic pal has generated a presentation for you. But, for the time being, AIs can’t read minds, so it’s likely that you’ll want to modify the slides. Please do! We didn’t forget about those time constraints you’re facing, so thanks to the editing tools provided by one of our sister projects —shoutouts to Wepik — you can make changes on the fly without resorting to other programs or software. Add text, choose your own colors, rearrange elements, it’s up to you! Oh, and since we are a big family, you’ll be able to access many resources from big names, that is, Freepik and Flaticon . That means having a lot of images and icons at your disposal!

How does it work?

Think of your topic.

First things first, you’ll be talking about something in particular, right? A business meeting, a new medical breakthrough, the weather, your favorite songs, a basketball game, a pink elephant you saw last Sunday—you name it. Just type it out and let the AI know what the topic is.

Choose your preferred style and tone

They say that variety is the spice of life. That’s why we let you choose between different design styles, including doodle, simple, abstract, geometric, and elegant . What about the tone? Several of them: fun, creative, casual, professional, and formal. Each one will give you something unique, so which way of impressing your audience will it be this time? Mix and match!

Make any desired changes

You’ve got freshly generated slides. Oh, you wish they were in a different color? That text box would look better if it were placed on the right side? Run the online editor and use the tools to have the slides exactly your way.

Download the final result for free

Yes, just as envisioned those slides deserve to be on your storage device at once! You can export the presentation in .pdf format and download it for free . Can’t wait to show it to your best friend because you think they will love it? Generate a shareable link!

What is an AI-generated presentation?

It’s exactly “what it says on the cover”. AIs, or artificial intelligences, are in constant evolution, and they are now able to generate presentations in a short time, based on inputs from the user. This technology allows you to get a satisfactory presentation much faster by doing a big chunk of the work.

Can I customize the presentation generated by the AI?

Of course! That’s the point! Slidesgo is all for customization since day one, so you’ll be able to make any changes to presentations generated by the AI. We humans are irreplaceable, after all! Thanks to the online editor, you can do whatever modifications you may need, without having to install any software. Colors, text, images, icons, placement, the final decision concerning all of the elements is up to you.

Can I add my own images?

Absolutely. That’s a basic function, and we made sure to have it available. Would it make sense to have a portfolio template generated by an AI without a single picture of your own work? In any case, we also offer the possibility of asking the AI to generate images for you via prompts. Additionally, you can also check out the integrated gallery of images from Freepik and use them. If making an impression is your goal, you’ll have an easy time!

Is this new functionality free? As in “free of charge”? Do you mean it?

Yes, it is, and we mean it. We even asked our buddies at Wepik, who are the ones hosting this AI presentation maker, and they told us “yup, it’s on the house”.

Are there more presentation designs available?

From time to time, we’ll be adding more designs. The cool thing is that you’ll have at your disposal a lot of content from Freepik and Flaticon when using the AI presentation maker. Oh, and just as a reminder, if you feel like you want to do things yourself and don’t want to rely on an AI, you’re on Slidesgo, the leading website when it comes to presentation templates. We have thousands of them, and counting!.

How can I download my presentation?

The easiest way is to click on “Download” to get your presentation in .pdf format. But there are other options! You can click on “Present” to enter the presenter view and start presenting right away! There’s also the “Share” option, which gives you a shareable link. This way, any friend, relative, colleague—anyone, really—will be able to access your presentation in a moment.

Discover more content

This is just the beginning! Slidesgo has thousands of customizable templates for Google Slides and PowerPoint. Our designers have created them with much care and love, and the variety of topics, themes and styles is, how to put it, immense! We also have a blog, in which we post articles for those who want to find inspiration or need to learn a bit more about Google Slides or PowerPoint. Do you have kids? We’ve got a section dedicated to printable coloring pages! Have a look around and make the most of our site!

The World's Best AI Presentation Maker

Key features of our AI presentation maker

Use AI to create PPTs, infographics, charts, timelines, project plans, reports, product roadmaps and more - effortless, engaging, and free to try

Effortless Creation

Instantly transform ideas into professional presentations with our AI-driven design assistant.

Personalized Design

Automatically receive design suggestions tailored to your unique style and content.

Anti-fragile Templates

Employ templates that effortlessly adapt to your content changes, preserving design integrity.

PowerPoint Compatibility

Efficiently export your presentations to PowerPoint format, ensuring compatibility and convenience for all users.

Ensure consistent brand representation in all presentations with automatic alignment to your visual identity.

Seamless Sharing

Share your presentations effortlessly, with real-time sync and comprehensive access control

Analytics &Tracking

Leverage detailed insights on engagement and performance to refine your presentations.

Multi-device Compatibility

Edit and present from anywhere, with seamless access across all your devices.

Multilingual Support

Reach a global audience with presentation AI that supports multiple languages.

Idea to Deck in seconds

ChatGPT for Presentations Create stunning PPTs at the speed of thought with the world's best AI slide maker. You focus on the story. We handle the fine print.

Creative power that goes way beyond templates

Impress your audience with professional and engaging presentations created through AI. Easy to customize. Hard to go wrong.

Brand consistent

Ensure that your presentations match your brand's style and messaging through our proprietary "Brand Sync" feature.

Presentations.AI is simple, fast and fun

Bring your ideas to life instantly

You bring the story. We bring design.

A collaborative AI partner at your command

Create at the speed of thought.

10 Best AI Presentation Generators (July 2024)

Unite.AI is committed to rigorous editorial standards. We may receive compensation when you click on links to products we review. Please view our affiliate disclosure .

In the digital age, AI-powered presentation generators are revolutionizing the way we create and deliver presentations. These tools leverage artificial intelligence to streamline the creation process, enhance visual appeal, and boost audience engagement. Here, we discuss the top 10 AI presentation generators that can help you elevate your next presentation.

Create presentations using AI with Plus AI for Google Slides

This tool enables users to create presentations and edit slides using Generative AI in Google Slides.

The AI-powered suggestions are a game-changer. It's like having a personal presentation assistant. The process is extremely simple, s tart with a prompt to generate a customizable outline, then watch as the AI turns it into slides in just a few minutes.

Once this is complete you have multiple options including rewriting the content to change the tone, or remixing the slide to transform the content into a specific layout.

Best of all, Plus AI will generate an outline, which you can customize before generating the presentation itself. To offer additional flexibility, when generating your slides, you can choose a visual theme. After the slides are generated, you can edit them just like any other presentation in Google Slides, export them for PowerPoint, and continue to edit them with Plus AI.

Top Features of Plus AI

Powered by the latest in Generative AI
Integration between Google Slides and Powerpoint is seamless
It creates a presentation that needs only minor editing when used with detailed prompts
The ability to rewrite content on slides is a game-changer

Use discount code: UNITEAI10 to claim a 10% discount .

Read Review →

Visit Plus AI →

2. Slides AI

SlidesAI - AI Powered Text To Presentation

Slide AI simplifies the presentation-making process. Users start by adding their desired text into the system. This text forms the foundation of the presentation, with Slide AI's intelligent algorithms analyzing and structuring the content into a visually appealing format. This innovative approach not only enhances efficiency but also democratizes design skills, allowing users to focus on content quality without worrying about design complexities.

Understanding the significance of personalization, Slide AI offers extensive customization options. Users can select from a range of pre-designed color schemes and font presets to align the presentation's aesthetics with their message or brand identity. For those seeking a unique touch, the platform provides tools to create custom designs, offering unparalleled flexibility in tailoring the look and feel of presentations.

3. Beautiful.ai

How to create a presentation in Beautiful.ai

Beautiful.ai is more than just a presentation tool; it's a smart assistant that helps you craft compelling narratives. As you begin to personalize your presentation, Beautiful.ai starts to understand your needs, offering suggestions for further enhancements. This predictive feature is a game-changer, making the design process more intuitive and less time-consuming.

But the innovation doesn't stop there. Beautiful.ai's voice narration feature adds an extra layer of communication, making your content more engaging. Imagine being able to narrate your slides, adding a personal touch to your presentation. This feature can be particularly useful for remote presentations, where the personal connection can sometimes be lost.

Top features of Beautiful.ai

Anticipates user needs and offers suggestions
Facilitates the creation of clear, concise presentations
Voice narration feature for enhanced communication

Visit Beautiful.ai →

4. Slidebean

Slidebean is a web-based presentation tool that revolutionizes the way presentations are made. With just a few clicks, users can create powerful presentations that leave a lasting impression. The beauty of Slidebean lies in its ability to separate content creation from slide design. This means you can focus on what matters most – your message – while Slidebean takes care of the design.

Slidebean is particularly suitable for small to medium businesses that may not have a dedicated design team. Even users with zero design skills can create professional-looking slides, thanks to the collection of design templates, premium fonts, and high-end color palettes. Slidebean is not just an alternative to PowerPoint and Keynote; it's a step up.

6. Synthesia

Synthesia is a robust AI presentation maker that stands out for its user-friendly interface and unique features. One of its standout features is the ability to create your own AI avatar. This means you can add a personal touch to your presentation, making it more engaging and memorable.

With Synthesia, you don't need to be an expert to create high-quality presentations. The tool offers a wide range of professionally designed video templates that you can use as a starting point. From there, you can customize your presentation to suit your needs. Whether you're presenting to a small team or a large audience, Synthesia has you covered.

Top features of Synthesis:

User-friendly interface
Allows creation of personalized AI avatar
Offers a wide range of professionally designed video templates

Visit Synthesia →

7. Simplified

Simplified is an AI presentation maker designed with collaboration in mind. It enables teams to work together seamlessly, creating presentations with the help of AI. This means you can collaborate with your team in real-time, making changes and seeing updates instantly.

After the AI generates a presentation, you can customize fonts, colors, and textures to make your presentation more impactful. You can also convert your slides into a video presentation by adding transitions. This feature can be particularly useful for remote presentations, where visual engagement is key.

Top features of Simplified:

Designed for team collaboration
Allows customization of fonts, colors, and textures
Can convert slides into video presentations

Visit Simplified →

8. Sendsteps

Sendsteps is a drag-and-drop AI presentation maker that simplifies the creation process. It's not just about creating slides; it's about creating an interactive experience for your audience. With Sendsteps, you can add interactive elements such as polls, SMS voting, quizzes, etc., to your presentation, making it more engaging and interactive.

One of the standout features of Sendsteps is its multilingual support. You can create presentations in more than 11 languages, including Spanish, Italian, Portuguese, French, and Dutch. This makes it a great tool for international teams or for presentations to a global audience.

Top features of Sendsteps:

Drag-and-drop interface
Offers interactive elements like polls, SMS voting, quizzes
Supports creation of presentations in more than 11 languages

Visit Sendsteps →

Prezi is a powerful AI presentation maker that can transform your ordinary slides into impactful presentations. It's not just about adding slides and text; it's about creating a narrative that captivates your audience. With Prezi, you can add a dynamic flow to your presentation, making it more engaging and memorable.

However, Prezi offers limited customization options after you choose a template. This means that while you can create a stunning presentation quickly, you may not have as much control over the final look and feel. Despite this, Prezi is a great tool for those who want to create a professional presentation quickly and easily.

Top features of Prezi:

Transforms ordinary slides into impactful presentations
Offers limited customization options after template selection

Visit Prezi →

Kroma is a popular AI presentation tool used by large organizations such as Apple and eBay. It gives you access to over a million creative assets and numerous data visualization elements, allowing you to create a visually stunning presentation. Whether you're presenting data, sharing a project update, or pitching a new idea, Kroma can help you do it.

One of the standout features of Kroma is its integration with MS PowerPoint and Apple’s Keynote. This means you can easily import your existing presentations and enhance them with Kroma's powerful features.

Top features of Kroma:

Used by large organizations like Apple and eBay
Provides access to over a million creative assets and data visualization elements
Can be easily integrated with MS PowerPoint and Apple’s Keynote

Visit Kroma →

In the digital age, AI-powered presentation generators are revolutionizing the way we create and deliver presentations. These tools utilize artificial intelligence to simplify the creation process, enhance visual appeal, and increase audience engagement. By leveraging AI, users can quickly produce professional presentations that would typically require extensive time and design skills. Features such as personalized templates, voice narration, real-time collaboration, and multilingual support make these tools versatile and accessible for various needs. Adopting AI-driven presentation tools can greatly improve the quality and impact of your presentations, making them more engaging and effective.

10 Best AI Game Generators (July 2024)

10 Best AI Voice Changer Tools (July 2024)

Alex McFarland is an AI journalist and writer exploring the latest developments in artificial intelligence. He has collaborated with numerous AI startups and publications worldwide.

15 Best AI Presentation Makers in 2024 [Free & Paid]

Written by: Idorenyin Uko

Creating a presentation from scratch can be time-consuming. Managing moving parts like content, design and visuals adds to the complexity.

The good news: AI is revolutionizing the way presentations are created. AI presentation makers leverage the power of artificial intelligence to simplify the process of creating visually appealing and impactful presentations. Anyone, regardless of their design experience, can whip up stunning presentations, pitch decks, slide decks and more in a fraction of the time.

Yet, with so many AI presentation makers flooding the market, making a choice can be overwhelming. We’ve got you covered!

In this article, we’ll review the 15 best AI presentation makers in 2024. Our extensive review covers their features, pricing, pros and cons so that you can make an informed decision.

Let’s get to it.

Beautiful.ai
Wonderslide

Visme’s AI-Powered Tools

Visme is an all-in-one visual design and content authoring software that lets you create presentations for different purposes.

Visme’s AI presentation maker takes it up a notch. With accurate prompts, you can generate ready-to-use presentation slides in minutes. The tool not only gives you a creative head start but also provides design suggestions and customization options for you to choose from.

Best AI Presentation Makers - Visme home page

The possibilities are endless. All you have to do is converse with the Visme AI chatbot, provide detailed information about the content type, tone and style and watch the AI do the rest. The tool cleverly transforms your prompts into beautiful, multi-page presentations. That way, you can spend more time honing your pitch to perfection! It's like having your very own presentation wizard at your fingertips.

Visme isn’t just an AI presentation maker. It has other AI-powered tools like AI Document Generator , AI Report Writer , AI Business Plan Generator , AI Image Generator , AI Edit Tools and AI Text Generator. These tools can help you create stunning visual content in minutes and boost productivity.

Visme's drag-and-drop editor makes it easy for anyone with little to no design skills to create eye-catching pitch decks , slide decks and interactive presentations for sales , marketing , webinar and business .

Rich Library of Templates and Styles

The extensive template library in Visme means users will always have options to showcase their ideas. Visme has thousands of presentation templates for any purpose, use case, industry and more. Our professionally designed AI presentation templates ensure your slides have a polished and visually appealing look.

Array of Customization Options

The Visme editor is foolproof. This means anyone can customize their AI-generated presentation to fit their unique needs or tastes. The tool lets you customize every aspect of your presentation or project.

You can change the color theme of your presentation using the preset color themes or create your own color palette. It's also easy to modify the font type and color. You'll have access to 400+ font types to play with in Visme.

Extensive Library of Stock Photos/ AI Image Generator

Not satisfied with the images in your presentation? We've got you covered.

Visme’s royalty-free graphic library includes thousands of free icons, illustrations, stock photos , videos, 3D graphics, audio clips, charts and graphs to include in your presentations.

Or you can simply generate new ones with the AI image generator. There's also the option to upload your own image and use Visme's AI image touchup tools to beautify it.

Audio and Voiceover

Visme offers dozens of free audio clips you can attach to individual slides or set as background music for your entire presentation. In addition, you can record a voiceover for your next presentation. The audio clip will be saved to your audio library for reuse in other presentations.

Data Visualization

If you need to visualize data, Visme has over 20 charts, graphs and maps to choose from. You’ll also find 30+ widgets, tables and diagrams to display data in a snackable format and complement your data visualization needs. Plus, you can modify the color, values, legends and text for all of your data visualizations.

The best part of using Visme is that it supports integration with lots of third-party tools. For more advanced customization, you can connect your charts to live data or import data from other tools into your charts.

Animations and Interactive Elements

Ditch boring presentations and enliven them with animations and interactive elements available in Visme's editor. Engage your audience and keep them immersed with interactive navigations, transitions, hover effects, pop ups, embeddable content and more.

Animated 3D Graphics and Illustrations

Visme's animation software has over 450 3D animation graphics, illustrations and special effects. Not only are our 3D graphics incredibly versatile, but we guarantee they'll wow your audience and take your presentation to the next level.

Keep your presentations consistent with your brand by creating a brand kit with Visme. The kit includes your logo, fonts, colors and other visual assets.

You can either upload these assets manually, use a brand guideline template or use an AI-powered brand wizard. Using the Brand Design Tool is super easy. Just input your website URL and the wizard will grab your logo, fonts and colors and add them to your brand kit.

Collaboration

Collaboration is seamless with Visme, no matter the size of your team. Your team members can edit your presentation, leave comments and draw annotations in real-time or asynchronously.

With the Workflow feature , you can streamline the review, collaboration and project sign-off processes. You can assign specific slides to different team members, set due dates and require approvals.

Presenter Studio

Visme’s Presenter Studio lets you easily record projects and presentations for your audience to view at their own pace. Take advantage of the Presenter Notes feature to stay on track and recall important points while delivering your presentation.

Download and Sharing Options

Once your presentation is ready, there are several ways to share it with your audience. You can generate a shareable online link or an embed code that can be placed on a website. Plus, you can download your slides in different formats, including:

Image: JPG and PNG
Document: PDF & PDF with Bleed Marks
Video: MP4 and GIF
Present Offline: PPTX and HTML5
LMS Export Formats: SCORM and xAPI

Track how your audience has engaged with your presentation with Visme analytics. This tool offers valuable insights into metrics like views, unique visits, average time spent, average completion and more.

Visme’s pricing plans include:

Basic: FreeStarter: $29.00/month
Pro: $59/month
Visme for Teams: Contact Sales
Intuitive and easy-to-use editor
Ability to chat with the AI chatbot, meaning users are not limited in terms of style, tone, language, or other elements.
Full suite of AI-powered tools to help users streamline their content production.
Multiple design and customizable options.
Thousands of free icons, illustrations, stock photos, videos, 3D graphics, audio clips, charts and graphs to include in your presentations.
Unlimited number of template styles to choose from
A wide selection of data visualizations, including charts, graphs, maps and widgets
Tools that enable teams of all sizes to collaborate effectively.
A diverse collection of templates catering to different presentation needs and themes.
Robust animation and interactive features

Due to a wide variety of features, it may take some time to use all available options.

2. Slidesgo

Slidesgo is a popular online platform with free PowerPoint and Google Slides templates to elevate your presentations. The tool offers an AI PowerPoint maker that helps you generate presentations in minutes. It uses artificial intelligence to analyze content and automatically generate visually appealing slides, complete with images, videos and other design elements.

Best AI Presentation Makers - Slidesgo home page

Just type out your topic and choose your preferred style and tone. Then you can customize the template by choosing your own colors, adding and rearranging elements.

Intuitive AI presentation maker that can generate presentations quickly.
Easy Customization: Users can easily customize slides to suit their specific needs. They can change colors, fonts and images, as well as add or edit content to create unique presentations.
Regular Updates: Slidesgo regularly updates its template library, ensuring users can access fresh and contemporary presentation designs.
User-Friendly Interface: The platform features a user-friendly interface. Users can easily browse through templates, preview them and download the ones they like without any hassle.
Compatibility: Templates provided by Slidesgo are compatible with popular presentation software, including Microsoft PowerPoint and Google Slides.

Slidesgo has two pricing plans:

Premium: $5.99/month/user
Education: $3.50/month/user
AI presentation software saves time as users don't need to start from scratch.
Supports more than 13 languages.
Interface is easy to navigate and use.
Number of free templates is limited.
Limited customization of design elements and layout alterations.
Prompts, writing tone and style are limited. Users cannot create prompts beyond the provided options or criteria.
Some bugs and layout limitations
Animation and interactive elements are limited.
Pricing is based on the number of users.

3. Beautiful.ai

Beautiful.ai is an AI-powered presentation maker designed to simplify the process of creating visually appealing and engaging presentations.

Best AI Presentation Makers - beautiful.ai home page

The DesignerBot offers users an innovative platform that leverages artificial intelligence to automate design elements, allowing for stunning presentations without the need for extensive design skills.

Automated Design: The AI PowerPoint generator automatically arranges text, images and data in an aesthetically pleasing manner, saving users time and effort in designing each slide.
AI Writer: Beautiful.ai can summarize, expand or rewrite text in a different tone.
Text to Image Generator: Users can generate an Al image with a detailed search prompt.
Data Visualization: Beautiful.ai can transform raw data into interactive and visually appealing charts and graphs, simplifying complex information for easy understanding.
Brand Customization: Users can customize AI-generated presentations to match their brand colors, fonts and logos, ensuring brand consistency across presentations.
Collaboration: Beautiful.ai allows for real-time collaboration, enabling teams to work together on presentations, share feedback and make edits simultaneously.
Intuitive Interface: The platform features a user-friendly interface with drag-and-drop functionality, making it accessible to users with varying technical expertise. Integrations: Supports integrations with Slack, Dropbox, PowerPoint and Monday.com.

Beautiful.ai offers three paid plans.

Pro: $12/month
Team: $50/month
Enterprise: Contact Sales
Rich media library containing millions of free stock photos, videos and icons.
Supports real-time collaboration.
Customize templates to align with users’ brand identity.
Ability to add voice narration over slides.
Doesn’t have a free plan.
Steep learning curve.
Limited design capabilities and interactive elements.
Only supports integrations with a handful of third-party tools.

4. Storydoc

Storydoc is an innovative AI-powered presentation maker that transforms the way presentations are created and delivered. It combines the power of artificial intelligence with storytelling techniques, enabling users to craft compelling narratives and visually engaging presentations seamlessly.

Best AI Presentation Makers - Storydoc home page

Professional Templates: Access pre-made templates for the most popular use cases.
AI-Driven Design: The platform uses AI algorithms to automate presentation creation. It structures and writes your content, assigns a design template and optimizes performance.
AI Writing Assistant: Generate any text, rephrase to perfection and brainstorm ideas.
AI Visual Assistant: Instantly generate any image you can imagine directly in your slides.
Automatic Analytics Insights : Get full visibility into how people engage with your slide deck.
Integrations : Connect your favorite tools to improve business processes.

Storydoc’s pricing plans includes:

Starter: $40/month/ user
Pro: $60/month/ user
Supports integrations with a vast number of third-party software.
AI-powered design results in professional-looking presentations—great for users without graphic design skills.
Workflow is simple and intuitive.
Modern user interface.
Limited number of templates.
Rigid Platform.
Limited options to tailor templates, fonts and colors to match brand identity and create a unique visual style.
Pricing is on the high side.
Cannot embed presentations through an iframe or embed.

Canva is a popular online design platform that offers a user-friendly AI-powered presentation maker. With the Magic Design for Presentations, you can generate a first draft of your presentation instantly.

Best AI Presentation Makers - Canva home page

Simply input your text and watch as it transforms into a well-organized outline, vibrant slides and compelling content.

Template Library: Canva offers a vast collection of professionally designed templates specifically tailored for presentations. Users can choose from various themes, styles and layouts.
Library of Assets: Get access to a library of millions of photos, icons, graphics, media elements and more.
Drag-and-Drop Interface: The intuitive drag-and-drop interface makes it easy to add text, images, video and other elements to slides.
Real-time Collaboration: Ability to collaborate and get team members on the same page at the same time.
Brand Kit: Users can store your logo, brand colors and fonts to maintain brand consistency.
Magic Write: Easily generate, summarize, expand and re-write text.
AI Photo Editing: Quickly erase, add to, edit and enhance your photos using AI-powered photo editing tools.

Let’s take a look at Canvas’ pricing plan

Canva Free: $0/month
Canva Pro: $14.99/ month
Canva for Teams: $29.99/month
Intuitive and user-friendly interface.
Supports collaboration across teams of all sizes.
Offers a diverse range of templates suitable for different industries.
Offers an AI writing tool and an AI photo editing tool.
Free plan only provides basic features and some advanced elements and templates are behind a paywall.
Users might need some time to explore all the features, especially the advanced customization options.

6. Design.AI

Design.AI offers a cutting-edge AI presentation maker designed to simplify the process of creating visually appealing and impactful presentations. This all-in-one platform provides a range of powerful features to enhance your creative projects.

Best AI Presentation Makers - Designs.ai home page

With AI writing assistance, a logo maker, a video presentation creator and natural-sounding AI voiceovers, it's your go-to toolkit for creating compelling content.

Smart Templates: Design.AI boasts a wide selection of smart templates tailored for various presentation needs. These templates adapt to the content, ensuring consistent and polished designs across slides.
Branding Kit: Users can apply consistent branding on all their presentations
AI Writer: Create powerful, compelling marketing copy using AI to boost engagement and sales.
Designmaker: Users can automatically generate thousands of design variations for creative projects.
Speechmaker: Convert text into realistic voiceovers and add them to your presentation
Automated Design Elements: The AI algorithms automatically handle design elements, such as layout, color schemes and typography, streamlining the creation process and maintaining a cohesive visual style.
Millions of Design Assets: Rich library of stock images, graphics, shapes, frames and stickers.
Content Enhancement: Design.AI provides premade color palettes, font pairs and illustrations, helping users refine their designs for clarity and impact.

Designs.AI has three pricing plans:

Basic: $29/month
Pro: $69/month
Enterprise: $199/month
Simple and user-friendly design interface.
Offers a wide array of additional tools.
No free plan.
While automation is a strength, users might find limitations in terms of highly specialized or unique design needs.
Doesn’t provide robust analytics or statistics for projects.
Lacks data visualization capabilities.
Users might require time to familiarize themselves with the platform's features.

7. Simplified

Simplified offers an advanced AI presentation maker that revolutionizes the way presentations are created. The text to presentation AI is crafted to simplify the creative process for users of all skill levels.

Best AI Presentation Makers - Simplified home page

With the power of artificial intelligence, Simplified streamlines your design, enhances your creativity and improves your presentation quality.

Premade Templates: Simplified offers a vast selection of smart templates designed for various uses.
AI-Design Assistance: The platform offers AI-driven design suggestions, helping users create polished and professional slides effortlessly. From layout to color schemes, AI ensures a consistent and visually appealing design.
Collaborative Tools: The tool offers real-time collaboration features that improve teamwork and productivity.
AI-Powered Tools: Simplified provides a wide range of AI-powered tools like AI writer, AI image generator, magic resizer and so on.
Design Customization Tool: An intuitive drag-and-drop interface lets users easily customize their design. Users can easily add text, images, videos and other elements to their presentation.
Brand Kit: Users can create custom brand kits for their projects and business branding.

Simplified offers three pricing plans for its AI-Powered Graphic Design Tools, Stock Photos & Templates:

Free Forever
Pro: $9/month
Business: $15/month
Interface is easily navigable.
Wide range of smart AI-powered tools.
Rich library of stock images, icons and other visual assets.
Turn presentations into a video project.
Offers multiple export formats (PNG, JPG, PDF and SVG).
Customization features are basic and limited.
Limited number of predesigned templates.
Basic animation features.
Limited Data visualization tools.

Tome is an AI-powered presentation maker that helps users create professional and engaging presentations without any design skills. It uses artificial intelligence to analyze content and automatically generate visually appealing slides, complete with images and animations.

Best AI Presentation Makers - Tome home page

Users can simply input their text and data, select a template or theme and let Tome do the rest.

Real-Time Collaboration: Tome AI presentation maker allows for collaboration and real-time feedback, making it ideal for teams and businesses.
Third-Party Integration: Tome supports integration with various third-party tools such as Typeform, Google Sheets, Figma, Miro and others.
AI-powered Designs: Automated slide creation using AI technology.
Turn Documents into Presentations: Paste documents into Tome and convert them into structured narratives in a single click.
AI Image Generator: Generate unique and professional images from text prompts.
Robust Library of Brand Assets: Search Tome’s image libraries or upload your own.
AI Writer: Fine-tune your copy by using AI to rewrite text, adjust tone and reduce or extend the length.
Free Forever: $0
Pro: $8/month/users
Enterprise: Contact for Sales
Easy to use, even for those with no design experience.
Saves time by automating the design process.
Produces high-quality, visually appealing presentations.
Collaboration tools make it ideal for teams.
Provides tools for incorporating animations, videos, graphs and more.
Limited customization options compared to other presentation software.
Occasional glitches or errors in AI-generated slides.
Limited control over design elements.
Not suitable for complex, data-heavy presentations.

9. Sendsteps

Sendsteps offers an innovative AI presentation maker that enables users to create engaging and impactful presentations in minutes. What makes Sendsteps stand out is its ability to facilitate real audience participation and engagement.

Best AI Presentation Makers - Sendsteps home page

AI-Generated Presentation Design: Users can describe the topic or upload a document and then the AI tool will generate interactivity, design and content.
AI Content Creator: You can easily generate compelling text, visually stunning word clouds, or interactive quiz questions to boost audience engagement.
Multi-Language Support: Create presentations in 86 languages, including English, Spanish, Dutch, Portuguese, Italian and French.
Interactive Quizzes: Sendsteps supports interactive quizzes, enabling presenters to create engaging quizzes to test audience knowledge and enhance participation.
Live Polls and Surveys: Sendsteps enables presenters to conduct live polls and surveys during presentations, allowing audience members to participate and provide instant feedback.
Audience Feedback: Sendsteps' AI analyzes audience responses, providing valuable insights into audience sentiment and engagement levels.

Sendsteps’s pricing tiers include

Free: $0.00/month
Starter: $13.99/month
Professional: $33.99/month
Easy to use interface, even for those with no design experience.
Offers a wide range of customizable templates and themes.
Provides a comprehensive suite of real-time audience engagement tools, including live polls, quizzes and surveys.
Support for multiple languages makes it accessible to a global audience.
Limited control over design elements compared to traditional presentation software.
Not suitable for highly complex or data-intensive presentations.
Limited design assets and customization options.
Occasional glitches or errors in the AI-generated slides.
Limited integration with other apps and services compared to some other presentation software.

10. Decktopus

Decktopus is an AI-driven presentation maker that aims to simplify the process of creating visually appealing and professional presentations. It combines intuitive design elements with artificial intelligence technology to help users craft engaging presentations with ease.

Best AI Presentation Makers - Decktopus home page

AI Content Suggestions: The platform provides AI-driven content suggestions, including target audience, purpose text and visuals. This helps users refine their message and enhance the overall quality of their presentations.
Smart Templates: Decktopus offers a range of smart templates that automatically adjust based on the content, ensuring consistency and aesthetics throughout the presentation.
Brand Customization: Users can easily customize and personalize the AI-generated content, slide layouts, colors, fonts and graphics to align with their brand identity and presentation style.
Ease of Use: The user-friendly interface and drag-and-drop functionality make it easy for users, even those without design skills, to create professional-looking presentations.
Collaboration: Decktopus enables collaboration, allowing multiple users to work on the same presentation simultaneously.
Pro AI: $14.99/month
Business AI: $48/user/month
Features an intuitive interface.
AI-driven content suggestions and smart templates save time and effort.
Support collaboration with an unlimited number of team members.
Rich library of design assets, including images, icons and graphics.
Support integrations with multiple third-party software.
Design customization options are basic.
Customization options are totally controlled by AI.
Doesn’t have a brand kit.
No option to import PowerPoint presentations.
Users cannot export in HTML.

Gamma AI is an advanced presentation maker that integrates artificial intelligence technology to streamline the presentation creation process. It is designed to help users create visually stunning and engaging presentations.

Best AI Presentation Makers - Gamma home page

This makes it an ideal choice for businesses, educators and professionals seeking an efficient and innovative presentation solution.

Smart Templates: Gamma AI offers a wide array of smart templates professionally designed for stunning presentations.
Brand Customization: Users can customize templates, fonts, colors and layouts to match their branding.
Export Capabilities: Ability to export presentations in PDF and PPT format.
Analytics: Users can measure audience engagement with built-in analytics.
AI-driven Content Suggestions: This feature helps users refine their message and enhance their content.
Real-time Collaboration: Multiple users can work on the same presentation simultaneously, share feedback and make edits in a collaborative environment.

Gamma’s pricing plans are as follows:

Free: $0/user/month
Plus: $10 /user/month
Pro: $20/user/ month
Presentations have a polished and professional look.
User-friendly interface makes the tool accessible to users with varying levels of technical expertise.
Limited export options.
Free plan shows limited change history.
Limited capability for highly specific or intricate design customization.

Plus is an innovative AI presentation maker that integrates artificial intelligence to simplify the presentation creation process. The tool makes it easy for individuals or businesses to generate AI presentations or edit slides with AI.

Best AI Presentation Makers - Plus home page

What makes Plus special is that it has seamless integrations between Google Slides and PowerPoint.

AI Design Assistance: The platform employs AI algorithms to provide content outlines and design suggestions and generate slides from text prompts.
Presentation Editing with AI: Users can insert slides, remix layouts or create new formats with text prompts with AI.
AI Writing and Rewriting Tool: You can modify the language and grammar, change the tone, lengthen, summarize or translate your text with Plus.
Custom Presentation Themes: Easily generate custom presentations and add your logo, custom fonts and colors to match your brand or ask AI to do it for you.
Multi-language Support: Plus AI can generate, edit and translate Google Slides presentations in Spanish, French, German, Portuguese, Italian and nearly any other language.

Below are the plan options in Plus AI

Free: Free forever
Slides:$15/user/month
Pro:$25/user/month
Enterprise: Contact sales for pricing
Offers multi-language support.
Real-time collaboration features available in Google Slides.
Super easy to use, so users are sure to have a smooth and hassle-free experience.
Supports integrations with a vast number of third-party tools like Slack, Notion, Confluence, Coda, Canva, etc.
Offers more than 100,000 character prompts.
Ability to automate workflows for future projects.
Functions as an add-on on Google Slides, but you need to have a Google account to use it.
Limited number of layouts and themes.
Design customization options in Plus are limited.
Lacks detailed analytics for tracking audience engagement.

13. Appy Pie

Appy Pie's AI presentation maker is a user-friendly and innovative tool designed to simplify the process of creating engaging presentations.

Best AI Presentation Makers - Appypie home page

By leveraging artificial intelligence technology, the platform helps users craft visually appealing slideshows without requiring extensive design skills.

User-Friendly Interface: Appy Pie Design offers an intuitive and user-friendly interface that makes it easy for anyone, regardless of their design expertise, to create presentations.
AI-Powered Features: The tool leverages the power of artificial intelligence (AI) to streamline the presentation creation process. It also offers AI-generated suggestions for text, images and design elements.
Extensive Template Collection: AI-Powered Appy Pie’s Presentation Template Collection offers a vast and diverse range of beautifully crafted designs, catering to every occasion and celebration.
Customization Options: Users can customize every aspect of their presentation, including layouts, text, fonts, colors, images and layouts.
Extensive Image Library: With a vast library of AI-generated images, illustrations, icons and backgrounds,
Custom Design: Appy Pie gives users plenty of options to enhance their presentations visually. You can also upload your visual to add a personal touch.

Appypie design starts at $8/month. Additional features attract extra usage costs.

User-friendly interface.
Offers a wide array of AI-powered design and productivity tools.
Supports integrations with a wide range of third-party tools.
Rich library of templates.
Real-time collaboration features are limited.
Customization options are basic.
Doesn’t offer a brand kit.

14. Wonderslide

Wonderslide is another AI-powered tool that helps you create presentations blazingly fast. Once you upload your draft slide, select your color, logo, themed images and fonts and the AI will handle the rest.

Best AI Presentation Makers - Wonderslide home page

Customization and Branding: Users can choose a color, font and style consistent with their company’s brand book.
AI-Powered Design: The platform provides AI-driven design suggestions.
Free Start: $0.00/month
Pay As You Go: $4.99 per one-time use.
Monthly: $9.99/month
Yearly: $69.00/year
Enterprise plan: Book a demo call
AI designer works with PowerPoint and Google Slides files.
Brand and customization options are limited.
Lacks collaborative design features.
Designs look amateurish.
Inability to create presentations from scratch, requiring a draft presentation.
Lacks animations and interactive elements.
Limited number of design assets, illustrations, icons and graphics.

15. SlidesAI

SlidesAI is an innovative AI-powered presentation add-on tool that simplifies the process of creating visually appealing and compelling presentations in Google Slides. Anyone, regardless of their design ability, can create presentation slides with AI in seconds.

Best AI Presentation Makers - Slides.AI home page

AI-Powered Design Assistance: The platform provide AI-driven design suggestions, including images, layout, color schemes and typography.
Magic Write: The AI-powered tool lets users generate high-quality outlines and text or rewrite existing content.
Integration: The tool supports easy integration with Google Slides.
Basic: $0.00/month
Pro: $10.75/month
Premium: $21.50/month
Team: Pricing varies based on the number of team members
Institution: Contact Sales
Supports 100+ languages.
Clean user interface.
No technical expertise is required to use the app.
The platform is rigid; you must install the tool as a Google Slides extension.
Limited download and export options.
Template library is limited.
Some users report technical glitches while using the tool.
Overall presentation designs aren’t impressive.

Visme is not just the best presentation maker . It offers a wide range of AI-powered tools to get your creative juices flowing and boost productivity, including:

AI Document Generator

AI Report Writer
AI Business Plan Generator
AI Image Generator
AI Edit Tools
AI Text Generator

Brand Wizard

This tool streamlines the process of creating documents like business proposals, newsletters, reports, ebooks, whitepapers, case studies, plans, etc. The tool ignites your creative spark as you generate your first draft and produce incredible documents that will wow your audience.

By using Visme, you get more than the AI document generator. With the AI business plan generator , you can produce investment-ready business plans in seconds. Visme’s AI report writer automates the process of writing and designing reports. It allows you focus on analyzing data and deriving meaningful insights rather than getting bogged down in the intricacies of report creation.

Visme AI Edit Tools

With the Visme AI TouchUp tools, you can modify the appearance of any image. Users can easily erase and replace objects they don’t want in your images, remove backgrounds and unblur low-quality, smudged or motion-blurred images.

In addition, the tool also lets you enlarge the size of your images without losing visual quality.

Visme AI Text Generator

Whether you need creative content, professional articles, marketing copy, or even academic papers, Visme’s AI text generator can assist you in producing high-quality, tailored text.

The tool is also handy for editing tasks. You can edit, proofread, lengthen, summarize and switch tones for your text.

Visme’s AI Image Generators

We’ve reviewed the 11 Best AI Image Generators in 2023 [Free & Paid] . Here’s what we found: Visme stands out as one of the best you can find on the market. The design possibilities are limitless. Users can select from several creative outputs, including photos, paintings, pencil drawings, 3D graphics, icons and abstract art.

The AI-powered Brand Wizard helps keep your design on brand. The wizard generates your brand's fonts and styles across beautiful templates. Simply input your website URL, confirm your brand colors and fonts, choose the branded template theme you like the most and watch the magic happen.

Easily Tap into the Power of AI with Visme

And there you have it—our comprehensive review of the finest AI presentation makers in 2024.

But hey, if you're on the hunt for an exceptional AI presentation maker that not only meets but exceeds your expectations, look no further than Visme! We highly recommend giving it a try.

Our review clearly shows that Visme offers an unparalleled array of features. Not only can you create captivating presentations with ease, but you also gain access to a treasure trove of content authoring and visual design tools. Plus, the added perks of Visme's AI-powered solutions take your creativity to a whole new level.

But that's not all! By choosing Visme, you unlock a world of possibilities. Explore an extensive library of professionally designed templates for presentations, infographics, reports, plans, social media graphics and other assets. Collaborate seamlessly with your team, add animations and interactive elements and choose from our vast library of icons, stock photos and videos to make your content exceptional.

Ready to get started? Sign up now and let Visme's AI presentation maker transform your ideas into captivating visual stories that dazzle your audience.

Create stunning presentations in minutes with Visme

Trusted by leading brands

Effortless Design Content in Minutes with the AI Design Generator

Supercharge your content creation and designs in minutes with the power of the AI Designer.

About the Author

AI Presentation Maker

Effortlessly create stunning presentations with our free ai presentation maker, designed to save you time and inspire your audience..

credit card not required

Magic Create

Presentation

Maximum pages: 1 page

Stock Media

Create impressive presentations with ai in minutes.

Tired of spending hours crafting presentations? Say hello to Fliki AI Presentation Maker, your ultimate solution for creating professional presentations in no time.

Our AI powerpoint generator empowers you to input your presentation idea and let AI do the heavy lifting. With AI-generated templates, premium stock media, and advanced features, you can transform your ideas into captivating presentations that leave a lasting impression.

Whether you're crafting pitch decks, educational presentations, marketing slideshows, or anything in between, our AI PPT generator is your go-to solution for captivating your audience and conveying your message effectively.

How to create a presentation in 3 simple steps

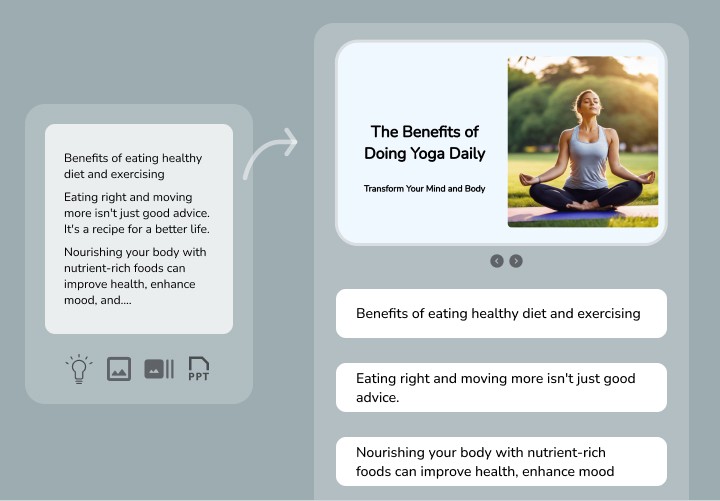
Write your presentation topic.

Begin by entering your presentation idea and selecting your preferred visual type - whether it's stock media or AI-generated media.

Converting text into a professional presentation with Fliki AI presentation maker

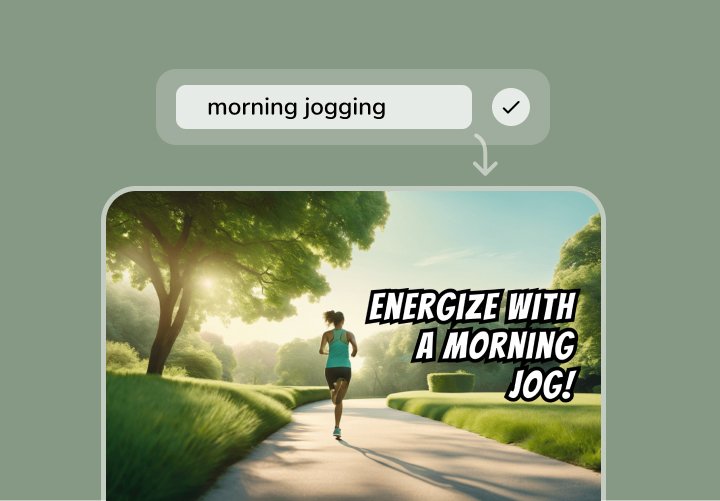
Customize your presentation

Personalize your presentation with different elements such as shapes, text, images, and media layers.

Generating an engaging slide on morning jog using Fliki AI presentation maker

Download your presentation

Once your presentation is perfected, download it in PPTX format.

Interface with a download button for Fliki AI presentation maker’s output

Loved by content creators around the world

5,000,000 +.

happy content creators, marketers, & educators.

average satisfaction rating from 5,500+ reviews on G2, Capterra, Trustpilot & more.

$95+ million

and 1,750,000+ hours saved in content creation so far.

A man with short dark hair smiling while wearing a black jacket, set against a blue sky background

Nicolai Grut

Digital Product Manager

Excellent Neural Voices + Super Fast App

I love how clean and fast the interface is, using Fliki is fast and snappy and the content is "rendered" incredibly quickly.

A woman with curly brown hair smiling, with a backdrop of green foliage

Lisa Batitto

Public Relations Professional

Hoping for something like this!

I'm having a great experience with Fliki so I was excited about this deal. My first project is turning my blog posts into videos, and posting on YouTube/TikTok.

Frequently asked questions

Yes, Fliki offers a tier that allows users to explore text to voice and text to video features without any cost.

You can generate 5 minutes of free audio and video content per month. However, certain advanced features and premium AI capabilities may require a paid subscription.

Fliki stands out from other tools because we combine text to video AI and text to speech AI capabilities to give you an all in one platform for your content creation needs.

Fliki helps you create visually captivating videos with professional-grade voiceovers, all in one place. In addition, we take pride in our exceptional AI Voices and Voice Clones known for their superior quality.

Fliki supports over 75 languages in over 100 dialects.

The AI speech generator offers 1300+ ultra-realistic voices, ensuring that you can create videos with voice overs in your desired language with ease.

No, our text-to-video tool is fully web-based. You only need a device with internet access and a browser preferably Google Chrome, to create, edit, and publish your videos.

An AI-generated presentation is created using artificial intelligence technology. It analyzes user input to generate engaging content, opening up exciting possibilities for various fields like business, education, and digital marketing.

Yes, our AI Presentation Maker provides customization options. You can make changes to colors, include brand assets, and more using our intuitive online editor.

Yes, our AI Presentation Maker is completely free to use. Create stunning presentations without any cost or subscription fees.

Once your presentation is ready, simply navigate to the download options. You can choose to download it in various formats such as PPTX or PDF directly from the platform. Additionally, if you prefer to have each slide as an individual image, you can download a zip file containing JPG, PNG, or WebP images of each slide.

Fliki supports voice cloning, allowing you to replicate your own voice or create unique voices for different characters. This feature saves time on recording and adds authenticity to your content.

It also opens up creative possibilities and assists individuals with speech impairments. With Fliki, you can personalize your content, enhance creativity, and overcome limitations with ease.

No, prior experience as a designer or video editor is not required to use Fliki. Our intuitive and user-friendly platform offers capabilities that make it super easy for anyone to create content.

Our Voice Cloning AI, Text to Speech AI, and Text to Video AI, combined with our ready to use templates and 10 million+ rich stock media, allow you to create high-quality videos without any design or video editing expertise.

You can cancel your subscription at anytime by navigating to Account and selecting "Manage billing"

Prices are listed in USD. We accept all major debit and credit cards along with GPay, Apple Pay and local payment wallets in supported countries.

Fliki operates on a subscription system with flexible pricing tiers. Users can access the platform for free or upgrade to a premium plan for advanced features.

The paid subscription includes benefits like ultra realistic AI voices, extended video durations, commercial usage rights, watermark removal, and priority customer support.

Payments can be made through the secure payment gateway provided.

Check out our pricing page for more information.

Stop wasting time, effort and money creating videos

Hours of content you create per month: 4 hours

To save over 96 hours of effort & $ 4800 per month

No technical skills or software download required.

Filter by Keywords

10 Best AI Tools for Presentations in 2024

Senior Content Marketing Manager

May 11, 2024

Presentations are a powerful way to share information, but building your slide deck is often time-consuming.

Artificial intelligence (AI) is revolutionizing how people put professional and engaging presentations together, allowing you to create polished presentations in seconds. With AI, say goodbye to tediously moving elements around on a slide and say hello to getting time back in your schedule to work on the stuff that matters most.

Ready to harness this presentation superpower? Learn more about AI presentation tools , what to look for, and some of the best AI presentation makers available in 2024.

What to look for in AI tools for presentations

1. beautiful.ai, 2. simplified’s ai presentation maker, 3. slidebean, 4. designs.ai, 6. presentations.ai, 8. kroma.ai, 10. deckrobot.

What are AI Tools for Presentations?

Various software and platforms use AI to help users create, enhance, and deliver visually appealing slides. These tools can assist with all aspects of the presentation creation process, from the initial creation to supercharging engagement.

Depending on the specific AI presentation tool, it can help you with tasks such as:

Designing stunning presentations: AI can understand and follow the rules for good design, enabling it to craft professional-looking slide decks that are visually appealing and relevant to your content
Creating content: Tell the AI writing tool what you want to write about, and it will generate content for each slide and even create your speech notes
Building visuals for data: Give the platform your data, and it can create easy-to-read visualizations of your information ready to add to your slide deck

AI presentation makers help you produce engaging content faster and connect with your audience more effectively. But with so many AI presentation makers available today, you’ll want to work with a few options and determine which suits your workflow and style best.

When looking for an AI presentation maker, you’ll want to find something that feels intuitive and has a user-friendly interface. You don’t want to spend hours learning how to use a new piece of software, and you shouldn’t need extensive technical expertise to put these tools to work.

You’ll also want to ensure that the AI tool you choose integrates well with the rest of your tech stack. A stunning presentation is no good if you can’t get it to work with your preferred software, such as Google Slides or Microsoft PowerPoint.

You should also look for AI-powered tools that offer the functionality you need. For example, maybe you love designing slides but aren’t strong at crafting engaging copy. In that case, look for tools that focus on content generation with interactive elements so you can flex your design skills.

Or, you may want an AI presentation generator that does everything, from designing graphics to writing copy. These are often paid tools, but you can use free trials to determine your best options for creating presentations.

10 Best AI Presentation Tools 2024

Beautiful.ai is an innovative AI presentation maker that aims to revolutionize how you create engaging presentations. The platform makes smart design recommendations through its intuitive interface and streamlines the creation process. You focus on your content while Beautiful.ai manages the aesthetics. Customizable templates, smart charts for data visualization, and analytics to track which slides get the most engagement from your audience are available.

Beautiful.ai best features

Insightful analytics give you information on which slides in your presentation are making the most significant impact in a professional or academic setting
Secure sharing helps protect sensitive information while making it easy to access for key stakeholders
Seamless integration allows you to design slides in Beautiful.ai and edit them in PowerPoint

Beautiful.ai limitations

While the templates offer beautiful designs, some users complain that there aren’t enough options compared with other platforms. Some users may want more control over their final design than the platform allows

Beautiful.ai pricing

Pro for individuals: $12/mo
Team for team collaboration: $40/mo
Enterprise for advanced security and support: Contact sales for a custom plan

Beautiful.ai ratings and reviews

G2: 4.7/5 (160+ reviews)
Capterra: 4.6/5 (70+ reviews)

AI presentation tools from Simplified's AI Presentation Maker

Simplified’s AI Presentation Maker promises to help you make on-brand presentations effortlessly. The platform handles image and content creation for any topic, and you can customize the results to suit your needs. All you have to do is tell the AI what topic you want to present, and it will generate the presentation in a few seconds.

Simplified best features

A range of pre-designed templates and a vast visual library, even for users on the free plan
Integration with all your favorite platforms, including Google Drive and Shopify
Easy real-time collaboration on presentations

Simplified limitations

The software can quickly become expensive, especially compared with similar services. It may be too costly for small organizations

Simplified pricing

Design Free: $0 for one seat
Design Pro: $6/month for one seat
Design Business: $10/month for five seats
Enterprise: Contact for pricing

Simplified ratings and reviews

G2: 4.6/5 (1800+ reviews)
Capterra: 4.7/5 (160+ reviews)

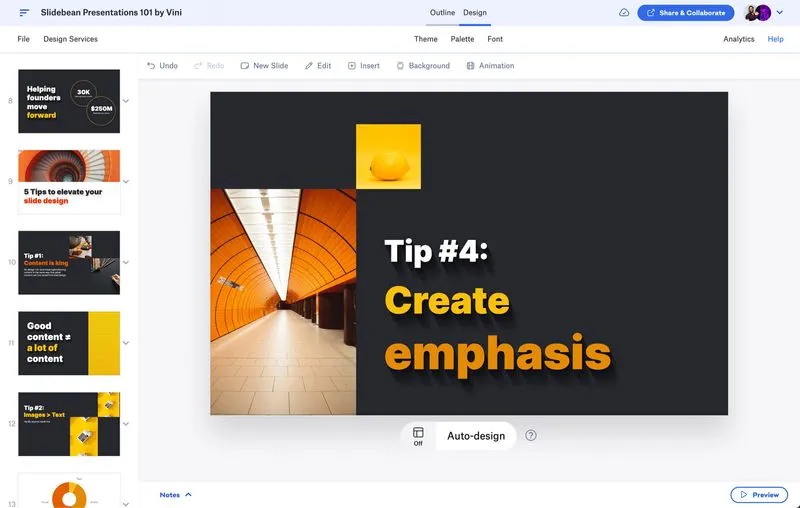
Slidebean is an AI presentation software that focuses on helping founders and startups create their pitch decks. It helps simplify the pitching process and ensures you have the right pitch for the right stage of company development. Whether you need an initial pitch deck, a marketing presentation, or a sales deck, Slidebean has solutions to suit your needs and help you get a yes.

Slidebean best features

Online sharing keeps your deck (and ideas!) secure while putting the right information in front of the right investors
Analytics track the activity of every slide in your deck so you know who viewed it, how many times, and when
Easy collaboration options help you get the whole team in on the action

Slidebean limitations

The user interface can be clunky, and some users may find editing AI-generated graphics and images difficult

Slidebean pricing

All Access: $199/year
Accelerate: $499/year

Slidebean ratings and reviews

G2: 4.5/5 (20+ reviews)
Capterra: 4.2/5 (50+ reviews)

Designs.ai offers a full suite of AI-powered creation tools. The platform offers AI writing assistance, a logo maker, a video presentation maker, and natural-sound AI voiceovers.

Those looking for help designing presentations will love the platform’s Designmaker, which creates visual content for you in seconds. Choose from a vast library of presentation templates, then give the platform your content and let it take care of the rest.

Designs.ai best features

The huge library of templates and design elements enables you to customize your AI presentations to suit your needs
One-click resize feature allows you to optimize your presentation for Instagram, mobile, projector screens, and other devices
Intuitive design editor means that you don’t have to be a master of graphic design to create a gorgeous deck

Designs.ai limitations

Exporting files can be slow and cumbersome

Designs.ai pricing

Basic: $19/month
Enterprise: Call for a custom quote

Designs.ai ratings and reviews

G2: 4.3/5 (6+ reviews)
Capterra: 4.5/5 (2+ reviews)

Pitch helps you create sleek presentations in seconds. Pick your template and add your content; you’ll soon have a beautiful deck ready to share. The platform allows you to share a link, present your presentation live, or even embed it on the web so you can direct viewers to it anytime. It has robust integration capabilities, connecting with tech-stack favorites like Slack, Vimeo, and YouTube.

Pitch best features

Great integration capabilities make it easy to add content to your deck and share it with others
Analytics help you track what’s working in your deck and see what you need to tweak
Great presentation tools make it simple to share, record, and present your deck

Pitch limitations

While the AI-generated slides are aesthetically pleasing, slide editing features can be clunky

Pitch pricing

Starter: $0, free forever
Pro: $8 per member per month
Enterprise: Contact for a custom quote

Pitch ratings and reviews

G2: 4.4/5 (40+ reviews)
Capterra: 4.9/5 (30+ reviews)

AI presentation tools from Presentations.ai

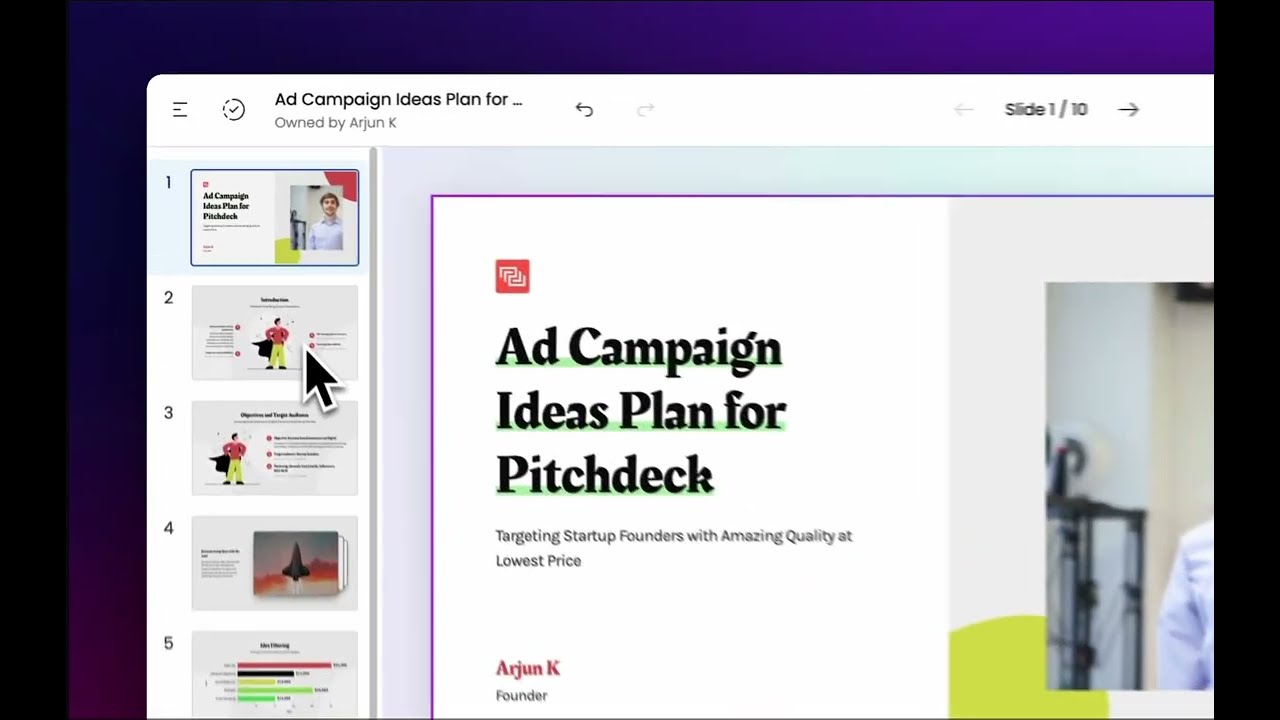
Presentations.ai aims to help you reduce presentation creation time while improving your overall presentation design quality. The platform uses AI technology to make creation effortless and offers many personalized design options. You can then share, track, and analyze your presentations to see how they perform with your audience.

Presentations.ai best features

Create presentations in seconds from a single prompt
Get the perfect final look with various presentation tools and customization options
Great branding options so you have a consistent, polished look for everything you create

Presentations.ai limitations

The platform focuses heavily on pitch decks and marketing presentations, so the templates may be frustrating for users looking to create educational or informative presentations. Some templates and slides are behind a paywall, limiting options for free users

Presentations.ai pricing

Starter: $0 (beta pricing)
Pro: $396 (beta pricing)

Presentations.ai ratings and reviews

Not available

Gamma uses natural language processing to help users create dynamic decks. Start writing your content, then use the built-in AI chatbot to change the look of your deck. When you’re happy with the deck, enter present mode and show your work off in a live presentation or send it as a webpage for users to view independently. It’s a flexible, user-friendly platform that helps you engage your audience.

Gamma best features

Change up the look of your slide deck at any time with the help of the AI-assisted presentation tool
Embed GIFs, charts, videos, and even websites to bring presentations to life
Receive instantaneous feedback on your presentations from viewers with quick reactions

Gamma limitations

Templates offer significant color customization, but there is little variation in layout and design

Gamma pricing

Starter: Free
Pro: Coming soon
G2: 4/5 (6+ reviews)
Capterra: 4/5 (1+ reviews)

Kroma.ai helps you create beautiful decks whether you present them to potential investors or need to share your ideas and data.

Simply pick your template, choose your colors, and add your logo. Then, use the grab-and-go expertly generated content to take your presentation to the next level, making it more persuasive and engaging with the help of industry leaders.

Kroma.ai best features

Choose content from industry experts to boost your professional presentation
Make your numbers stand out with robust data visualization tools
Create stunning presentations with expertly designed templates that ensure that you have the right format for the job

Kroma.ai limitations

Some parts of the user interface aren’t hugely intuitive
Some users may not care about the expert-written content, which is one of the platform’s big selling points

Kroma.ai pricing

Explorer: Free
Premium: $49.99 per user per month
Enterprise: $1,699 per year

Kroma.ai ratings and reviews

Tome wants to be your go-to AI presentation tool. Tell the platform what you want to do with a simple prompt, and it will generate images, copy, and slides to help you achieve your goal.

You can tweak every aspect of the design, asking the AI tool to change the tone or generate a new AI image in a different style. It’s also great for turning boring documents into dynamic presentations.

Tome best features

It helps you find and cite references that support your claims
Easy language translations permit you to your share presentations across the world
Excellent customizable templates allow you to create pitch decks, marketing presentations, and educational presentations

Tome limitations

Some users are encountering issues with the platform, though this could be because the tool is still in development

Tome pricing

Free Forever
Pro: $8 per person per month
Enterprise: Contact for custom pricing

Tome ratings and reviews

G2: 4.8/5 (20+ reviews)

DeckRobot is a handy plug-in that turns your drafts into polished presentation decks in seconds. It even ensures that your final deck complies with your corporate branding guidelines so you maintain consistent branding in everything you create. It’s a great way to reduce manual design time, and all your data stays securely on your servers.

DeckRobot best features

Plug-in for PowerPoint presentations takes the first draft of your presentation and turns it into a polished final deck
Your data stays secure because all information stays on your server
It allows you to redesign with preset corporate branding in one click

DeckRobot limitations

This plug-in is for PowerPoint, so if you’re using another platform, you’ll need to opt for another AI solution

DeckRobot pricing

Call for custom pricing

DeckRobot ratings and reviews

Receive the latest WriteClick Newsletter updates.

Thanks for subscribing to our blog!

Please enter a valid email

Free training & 24-hour support
Serious about security & privacy
99.99% uptime the last 12 months

The presentation software for everyone.

This is Beautiful.ai. It makes your whole approach to presentations easier – starting with design that works faster. Use it to win pitches, reimagine reports, and get better work done every day.

Create beautiful presentations in minutes

More than ever, ideas need to be presented meaningfully, easily, and without putting other work on hold. Beautiful.ai works smarter, so you can do great work faster.

Jumpstart your ideas

Start your presentation inspired. Look, we made it easy. Beautiful.ai's presentation software is filled with tons of smart templates for you to choose from, so it’s easy to start, finish and impress in no time.

And put formatting on autopilot

Beautiful.ai applies the rules of great design in real-time. Just add content and your slides adapt like magic. No resizing text or images. Ever.

And keep every slide on brand

Look your very best every time with beautifully designed themes. When you sign up, this presentation software unlocks millions of modern images and icons that reflect your brand. Now every slide is consistent–and consistently creative.

And impress in no time

With intuitive controls, dial up your productivity. Smooth animations bring your stunning slides to life, because boring presentations are so 1995.

Increase efficiency with time saving features

Beautiful.ai removes outdated steps so you get from messy ideas to the right message ASAP. Whether you’re working on one slide or an absurd amount of presentations, our presentation software helps organize your thoughts so your story comes to life fast.

Hundreds of pre-built slides

Start inspired with hundreds of customizable, beautifully designed smart slides in our slide gallery and save hours from having to start from scratch.

Simple intuitive controls

Create new layouts in seconds.

Smart templates have built-in layout variations that you can toggle to quickly visualize your content in different ways.

A really simple way to make killer presentations

Beautiful.ai has made creating presentations so simple and saved a ton of our team's time

Beautiful.ai is amazing in every sense of the word. I am able to easily create the best, most professional presentations.

It's so much more helpful, fast, and design-oriented than anything else I've tried

With absolutely no design background -- I'm creating beautiful - and powerful presentations

It’s like working side-by-side with a designer

Beautiful.ai helps me cut down time and focus on my content for a great presentation!

Meet your new productivity expert

Beautiful.ai is the best presentation software for businesses looking for tools that increase their productivity and for individuals who need advanced features and customizations for stunning online presentations.

Get a head start with hundreds of presentation templates

With galleries of Smart Slides and Presentation Templates to inspire you, it’s easy to get a headstart on pitches, reports, and training decks. Never stare at a blank page or look generic again.

Search for anything you need

Search for inspiration, existing content, or slide layout templates in our slide library, so you can get your creative juices flowing and not waste hours recreating old content.

Visualize your data

Bring your data to life with dozens of beautifully designed charts, diagrams and graphs. Powerful data visualization tools give you granular control over every detail.

Presentation templates for every use case

Present your best work, anytime, anywhere.

Export to power point, advanced sharing options, view on any device.

Save time by designing in Beautiful.ai and exporting to PowerPoint for a seamless workflow. You can even make edits to your slides in PowerPoint, when you upgrade to Pro .

With quick and easy sharing options, you can invite your colleagues via email, share a link, or embed your presentation on a website or blog.

Everything is created and stored on the cloud. So you can access and share your content anywhere and on any device.

Virtually every presentation tool you need.

As a presentation tool made by designers but geared towards everyone, Beautiful.ai comes fully loaded with dozens of essential presentation creation tools as well as many you didn’t even know you needed. Your only limit will be your imagination.

60+ Customizable Smart Slide Templates

Stay on-brand consistently with customizable themes

Bring ideas to life with automatic animations

Add audio or narration to your slides for context

Measure presentation metrics with viewer analytics

Millions of free photos, videos and icons

The ultimate presentation software for teams

Control slides, branding, and updates across your company. Beautiful.ai’s Team Plan has all the tools that make life easier–so you can make all the brilliant presentations you need.

Success Stories

Check out how other brands have secured funding, won business and closed the sale with Beautiful.ai. It’s time to present your best work ever.

“I haven’t opened PowerPoint since December of 2019. I have literally taken it off my taskbar at the bottom of my computer because I have no need to open it ever. So, that is fantastic.”

“Beautiful.ai allows you to tell a better story with less effort and more impact”

“Clients will often say, ‘Wow, you always have the best slide decks. How did you put that together?’ And they don’t realize that it took me 15 minutes before the meeting.”

Go from basic to beautiful in minutes.

Summarize PowerPoints with AI
Summarize Word documents with AI
Summarize PDF with AI
Generate PowerPoints with AI from text
Create Presentation with AI
GPT for Presentations
Chat with Document Groups
Import files from Cloud
Request Demo

Master presentations and documents with AI

Summarize PowerPoint or Word documents, generate presentations with AI and much more. Start using our AI to boost your productivity.

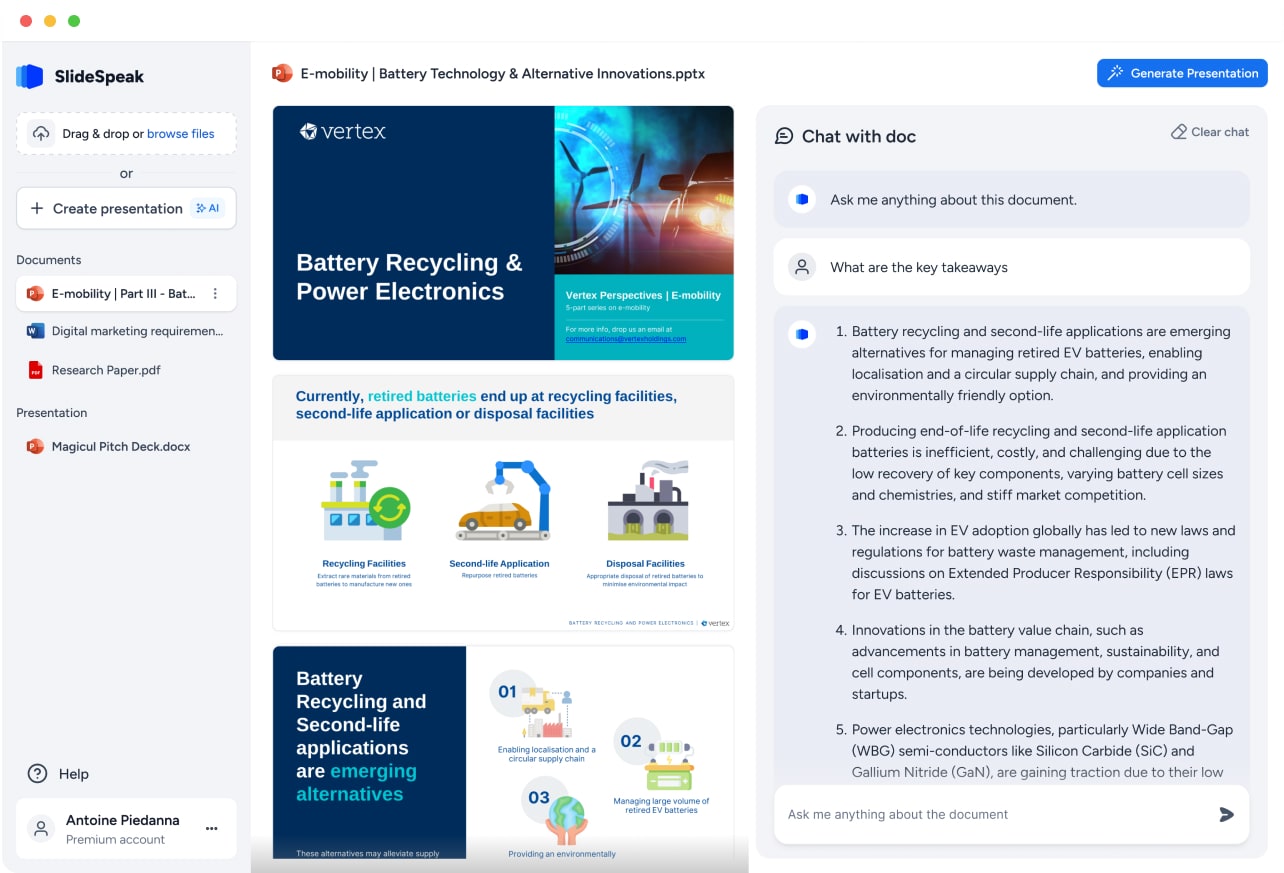
ChatGPT for PowerPoint slides and documents

Give our AI a document and watch the magic...

Simply upload your PPTX, Word or PDF file and ask our AI to summarize it for you. Our ChatGPT-powered platform will generate highly accurate summaries for you. Learn More

Use our AI to create presentations for you. Simply upload a document and ask SlideSpeak to generate a presentation based on the content. Learn More

Our AI understands the content of all documents you've uploaded. Simply ask questions, request summaries and much more.

As smooth as ChatGPT, but with your documents.

Upload your PowerPoint documents and ask questions about the content.

Generate Summaries
Generate Presentations
Ask literally anything...

Frequently Asked Questions

Stay up to date with our newsletter.

Read our blog

Articles how to use AI with Presentations, Word Documents and PDFs and more.

Top 5 AI PDF Translator Tools in 2024 that are Free

July 17, 2024
Comments Off on Top 5 AI PDF Translator Tools in 2024 that are Free

5 Ways how to use AI to Write a Resume

July 9, 2024
Comments Off on 5 Ways how to use AI to Write a Resume

6 Ways to Generate a Quiz with AI from Word Documents

June 24, 2024
Comments Off on 6 Ways to Generate a Quiz with AI from Word Documents

Your AI to generate presentations and summaries

Chat with your PowerPoint files, ask questions, get summaries, generate presentations and more.

No credit card required
Free to use

AI generate presentations and summaries.

Summarize and generate PowerPoint files with ChatGPT. Upload, chat, and gain new insights from your presentations. Use SlideSpeak AI to boost your productivity.

Help Center
Affiliate Program 💵
Call us: +1 ‪(512) 777-1759‬
Compress PowerPoint
Convert PowerPoint to PDF
Convert PowerPoint to PSD
Convert PowerPoint to Figma
Convert PDF to Word
Terms of Service

AI Presentation Generator

AI Presentation Maker

AI Image Generator

WORD to PPT

Reports to PPT

Outline to PPT

Research Papers to PPT

AI PDF Summarizer

AI WORD Summarizer

AI File Summarizer

AI Document Summarizer

Convert to PPT

AI Summarizer

Smart Slide Creation for Any Topic

What is an AI Presentation Generator?

An AI Presentation Generator leverages artificial intelligence to create presentations. It simplifies the process of slide creation, transforming a basic topic input into a comprehensive, visually appealing presentation. It's not just a PowerPoint AI; it's an intelligent system designed to intuitively understand your presentation needs and execute them flawlessly.

Intelligent Topic Analysis

Our AI Presentation Generator excels in understanding and analyzing the topic you provide. It's more than just a random presentation generator; it intelligently assesses your topic and curates content that's relevant and engaging. From creating a presentation title generator to selecting pertinent data, this tool ensures your slides are both informative and captivating.

AI-Designed Templates for Every Theme

Our AI Presentation Generator stands out with its array of AI-designed templates, ensuring each presentation is not only content-rich but also visually striking. AI-generated images are closely related to the topic and contents of your presentations, offering a perfect blend of design and relevance.

Log in or sign up to get started. Chat with our friendly AI about the topic you're thinking of. Check out the outline of our AI whips up for you. Like what you see? Give it a thumbs-up!

Pick Your Favorite Look: Dive into our collection of AI-designed templates and themes. Choose one that catches your eye and fits your story.

Relax and Watch the Magic Happen. Sit back and let AI do the heavy lifting for you! Get a customized design and stunning presentation filled with informative and professional content.

You can then edit the presentation using your preferred application, such as MS PowerPoint or Google Slides, or with our online AI Presentation Maker.

Superfast presentation creation

Join 500K professionals & educators

✓ Create with AI ✓ Convert to PPT with AI ✓ Compatible with PowerPoint ✓ Built in templates ✓ Auto Layout

Presentations that move audiences

Refine, enhance, and tailor your content quicker than ever before.

Enter a title or idea to get started.

Prezi is good for business

Keep teams engaged and customers asking for more

Prezi is smart for education

Make lessons more exciting and easier to remember

Millions of people — from students to CEOs — use Prezi to grab attention, stand out, and capture imaginations

The most engaging presentations happen on Prezi

Create with confidence

Professionally designed templates.

Choose from hundreds of modern, beautifully made templates.

Millions of reusable presentations

Focus on your own creativity and build off, remix, and reuse presentations from our extensive content library.

Real creative freedom

Open canvas.

Create, organize, and move freely on an open canvas. Create seamless presentations without the restrictions of linear slides.

Ready-made asset libraries

Choose from millions of images, stickers, GIFs, and icons from Unsplash and Giphy.

A presentation that works for you

Present in-person.

Have the confidence to deliver a memorable presentation with presenter notes and downloadable presentations.

Present over video conference

Keep your audience engaged by putting yourself in the center of your presentation.

Your own ideas, ready to present faster

Prezi AI is your new creative partner. Save time, amplify your ideas, and elevate your presentations.

The specialists on visual storytelling since 2009

From TED talks to classrooms. In every country across the world. Prezi has been a trusted presentation partner for over 15 years.

*independent Harvard study of Prezi vs. PowerPoint

See why our customers love us

Prezi is consistently awarded and ranks as the G2 leader across industries based on hundreds of glowing customer reviews.

Prezi powers the best presenters to do their best presentations

Free AI Presentation Generator

With Venngage's AI Presentation Generator, you can overcome a lack of inspiration or time constraints. Just enter your prompt, and your presentation will be ready instantly!

Browse through more presentations

How to write a prompt that generates the presentations you want?

Purpose and Topic: Clearly state the main purpose and topic of the presentation.

Target Audience: Identify the intended audience to tailor the content and style.

Key Points or Data: Specify essential points or data that need to be included

Sample prompts you can modify and use

“environmental presentation template: create a simple, elegant environmental presentation template focusing on sustainability and conservation”, “business proposal presentation template: create a modern business proposal presentation template highlighting finance and market analysis.”, “marketing strategy presentation: generate a marketing strategy presentation with creative, engaging visuals and data-driven content.”, “corporate business presentation proposal: design a corporate business presentation proposal with professional visuals and include a standard proposal structure.”, boost your engagement with personalized content.

AI algorithms can customize content for specific audiences, boosting engagement and effectiveness.

Using our AI Presentation Generator, you can now save hours on drafting and designing — jump straight to the fun part by delivering impressive results and enjoying the creative process!

Increase Your Productivity & Save Time

Starting a project is often the hardest part. Venngage's free AI presentation generator is designed to help you overcome this initial hurdle by quickly delivering a solid first draft. Within minutes, you'll have a ready-to-use presentation that requires minimal customization, yet is fully editable for further creative edits when needed.

Although AI sets a strong foundation, it can't capture every nuance. You can further customize by revising text, selecting colors, and rearranging elements to fully align with your vision and requirements.

Maintain Quality and Consistency Across Your Projects

Do you frequently create presentations? Generating fresh ideas and maintaining quality can become a daunting task, not to mention the challenge of innovative design. With an AI presentation generator, simply provide a custom prompt, and let our tool handle the rest — quickly delivering your finished presentation within minutes.

Enjoy peace of mind knowing that each of your presentations will feature consistent, high-quality designs and structure.

How Can You Create a Presentation in Under 5 Minutes?

Step 1: start with your topic.

What will your presentation be about? It could be anything from a business meeting to an unusual sighting of an exotic animal. Simply enter your subject to inform the AI of your focus.

Step 2: Select style and tone

Consider the design style you want for your presentation, like simple, abstract, geometric, or elegant, to ensure a perfect fit. Then, choose the tone that suits your message, from fun and creative to casual, professional, or formal. Decide how you want to captivate your audience.

Step 3: Define your AI Prompt

For optimal results when creating an AI-generated presentation template, keep these six tips handy: Define the objective, detail the audience, outline key points, specify style and tone, include visual preferences, and set constraints and length if you have any.

Step 4: Edit and customize as much as needed

Now that you have your slides, feel free to adjust them. Want to change the color scheme or move a text box? Don’t like the text? Customize it freely, however, you want and like! Use Venngage’s online editor's tools to tweak the slides to your preference.

Step 5: Download and share for free

Export your presentation in .pdf format and download it. Excited to share it with friends or colleagues? Create a link for easy sharing!

Venngage is more than just an AI presentation generator

Venngage is your one-stop shop for creating impactful presentations, infographics, reports, and more. It's a favorite among professionals, educators, and marketers for a reason:

Effortless Design

Browse a vast library of pre-made templates and customize them with your own text, images, and branding for a unique and polished look.

Drag-and-Drop Simplicity

The intuitive interface makes creating stunning visuals a breeze. Drag, drop, and edit with ease, and collaborate seamlessly with team members using built-in collaboration tools.

Data Made Clear

Transform your data into clear and informative charts and graphs. Import data directly from spreadsheets and let Venngage do the work.

Consistent Branding

Maintain a professional image with Venngage's Brand Kit. Save your company colors, fonts, and logos to ensure consistent branding across all your designs.

High-Quality Exports

Export your creations in various high-resolution formats like PDF, PNG, and many more, perfect for both digital and print use.

Can I customize the presentations generated by the AI?

Yes, you can fully customize all AI-generated templates on Venngage's platform.

Are there more presentation designs available?

Yes, Venngage offers a wide variety of presentation designs to suit different needs and preferences. Whether you're looking for something sleek and modern, or more detailed and data-focused, you'll find numerous options to choose from in our extensive template library.

Are the AI-generated presentation using Venngage’s tool copyright-free?

Yes, the AI-generated presentation created using Venngage's tools is copyright-free. You can use them for both personal and commercial purposes without any restrictions on copyright. However, it's always good practice to ensure that any externally sourced content you include is also cleared for use.

How many presentations can I generate for free?

The number of presentations you can generate for free on Venngage is currently unlimited.

Explore trending designs

Infographic Maker

Brochure maker, accessible design maker.

Samsung Newsroom's videos will no longer be supported on Internet Explorer. Please try a different type of web browser .

SmartThings
Custom range
Content Type
Press Release

Samsung Galaxy Z Fold6 and Z Flip6 Elevate Galaxy AI to New Heights

Meet the new galaxy ai upleveled by the unique foldable form factor of galaxy z series and the connected galaxy ecosystem galaxy buds3 pro enhances sound and communication quality through innovative ai capabilities.

Samsung Electronics today announced its all-new Galaxy Z Fold6 and Galaxy Z Flip6, along with Galaxy Buds3 and Galaxy Buds3 Pro at Galaxy Unpacked in Paris.

Earlier this year, Samsung ushered in the era of mobile AI through the power of Galaxy AI. 1 With the introduction of the new Galaxy Z series, Samsung is opening the next chapter of Galaxy AI by leveraging its most versatile and flexible form factor perfectly designed to enable a range of unique mobile experiences. Whether using Galaxy Z Fold’s large screen, Galaxy Z Flip’s FlexWindow or making the most of the iconic FlexMode, Galaxy Z Fold6 and Flip6 will provide more opportunities to maximize AI capabilities. Built on the foundation of Samsung’s history of form factor innovation, Galaxy AI uses powerful, intelligent and durable foldable experience to accelerate a new era of communication, productivity and creativity.

“Samsung’s long history of innovation has allowed us to lead in the mobile space, creating the foldable form factor and ushering in the mobile AI era. Now, we are excited to bring these two complementary technologies together and unlock new possibilities for users around the world,” said TM Roh, President and Head of Mobile eXperience Business at Samsung Electronics. “Our foldables meet the unique needs of every user and now enhanced by the power of Galaxy AI, Samsung is delivering an experience like never before.”

Samsung’s continued innovation for foldables has created the slimmest and lightest Galaxy Z series ever, optimized for portability. The perfectly symmetrical design with straight edge provides an aesthetically sleek finish while a new cover screen ratio on Galaxy Z Fold6 provides a more natural bar-type viewing experience. Along with design refinements, the new Galaxy Z series is engineered to provide even more durability, offering you greater peace of mind. The dual rail hinge structure is further supported by a strengthened folding edge, better distributing the shock of external impacts. Plus, enhanced layers on the main screen help to improve the crease while maintaining strength. The latest Galaxy Z series is also equipped with enhanced Armor Aluminum 2 and Corning® Gorilla® Glass Victus® 2 3 , making this the most durable Galaxy Z series yet.

In addition to being reliable, every element of the Galaxy Z series is also powerful. Both the Galaxy Z Fold6 and Flip6 are equipped with the Snapdragon® 8 Gen 3 Mobile Platform for Galaxy , 4 the most advanced Snapdragon mobile processor yet, combining best-in-class CPU, GPU and NPU performance. The processor is optimized for AI processing and offers enhanced graphics along with improved overall performance. The upgraded cooling system maximizes performance with a larger vapor chamber on Galaxy Z Fold6 and, for the first time ever, a vapor chamber on Galaxy Z Flip.

Galaxy Z Fold6: Large Screen Productivity Elevated by AI

The Galaxy Z Fold6 offers a range of AI-powered features and tools that maximize the large screen and significantly enhance productivity.

Note Assist 5 on Samsung Notes offers translation, summaries and auto formatting for simple and easy meeting notes. Plus, a newly embedded transcript feature enables transcription, translation and summarizing of voice recordings directly in Notes. Texts in PDF files can be translated and overlaid perfectly through PDF overlay translation feature in Notes 6 — and it even supports text in images and graphs. A newly added Composer 7 from Samsung Keyboard generates suggested text based on simple keywords for email and supported social media apps. For social media in particular, the Composer creates text that reflects your tone by analyzing previous posts. Additionally, the S Pen 8 experience is expanded further meeting with Galaxy AI on the Galaxy Z Fold6’s screen. All-new Sketch to image 9 allows you to create more sophisticated art pieces by generating image options when you simply sketch or draw on the photos in Gallery or Note screen.

The Galaxy Z Fold6 enables you to evolve the way you work, play and stay informed thanks to Samsung’s longstanding partnership with Google. The latest Google Gemini app 10 is fully integrated on the new Galaxy Z series, providing your own AI-powered assistant right on your phone. By simply swiping the corner of the screen or saying, “Hey Google”, you can bring up Gemini’s overlay and get help with writing, learning or planning. Gemini is integrated with some of your favorite Google apps, making it easy to organize a perfect travel itinerary by getting real-time flight and hotel booking information — and explore famous landmarks and the best routes to get there using Google Maps. When you want detailed information about a K-pop music video while watching YouTube on Galaxy Z Fold6’s large screen, you can access Gemini overlay in the multi-window split screen to ask questions. If you’re curious about who the artist is in the video, just long press the home button and circle, highlight or tap on screen — and Circle to Search 11 will offer instant search results.

Galaxy AI has also enhanced barrier-free communication on Galaxy Z Fold6. Maximizing its unique dual screen form factor, Interpreter 12 comes with a new conversation mode that enables both parties to conveniently view translations on the main and cover screens for more natural interactions. It also offers one-way translation, so you can easily understand when listening during lectures or any other type of presentation. Live Translate , 13 which translates phone calls directly on your device in real-time, is also now being extended beyond Samsung’s own native calling app to a selection of popular third-party apps.

From capturing to editing to viewing, AI-powered ProVisual Engine on the Galaxy Z Fold6 takes your creativity to the next level. The advanced editing experience with Photo Assist 14 on the large screen helps to effortlessly create professional-grade content. Portrait Studio 15 creates a variety of different portrait styles such as 3D cartoon or watercolor for more creative possibilities. And if you want to enjoy every second with a more detailed view, Instant Slow-mo 16 allows you to instantly slow a video by generating additional frames while maintaining a smooth viewing experience. You also have the option of saving or directly sharing your videos with friends and family so they can enjoy them as well.

Not only does Galaxy Z Fold6 allow you to create content, it allows you to enjoy it, too. Galaxy Z Fold6 offers an upgraded gaming experience, anchored by its powerful chipset and 1.6x larger vapor chamber for the ability to game for longer, while still maintaining performance. Vivid, life-like graphics are supported by Ray Tracing and are brought to life on a 7.6-inch screen 17 that offers a brighter display of up to 2,600nit to deliver more immersive gaming.

Galaxy Z Flip6: Creating Unique Experiences, Customized to You

The Galaxy Z Flip6 is not just optimized for portability, but it offers a range of new customization and creativity features so you can make the most of every moment.

The 3.4-inch Super AMOLED FlexWindow 18 has been enhanced yet again, enabling AI-assisted functions without even needing to open the device. And for those communications on-the-go, you can reply to texts with Suggested replies 19 which analyzes your latest messages to suggest a tailored response. With Galaxy AI, you can get the most out of your pocket-sized device, and many of these convenient features exist on FlexWindow. FlexWindow provides access to Samsung Health 20 updates and notifications and also allows you to select the next track you want to listen to on your music widget. Plus, FlexWindow offers more Widgets than ever, and allows you to check information from multiple Widgets simultaneously.

It wouldn’t be Galaxy Z Flip without a variety of ways for you to customize your device either. With the AI-powered Photo Ambient , 21 a wallpaper can change in real-time based on the time and weather. You can also easily create a unified look and feel with suggested screen layout options by analyzing your wallpaper — such as moving the clock and changing the frame color to ensure the background image stands.

Creativity also goes beyond FlexWindow. FlexCam continues to offer the most versatile camera experience and unlocks new creative options. With the new Auto Zoom , 22 FlexCam automatically finds the best framing for your shot by detecting the subject and zooming in and out before making any necessary adjustments. That way, you don’t have to choose between your friends or an incredible backdrop being in the shot — and it’s all hands-free.

New 50MP Wide and 12MP Ultra-wide sensors provide an upgraded camera experience with clear and crisp details in pictures. The new 50MP sensor supports 2x optical zoom for noise-free photos, while offering AI zoom for an advanced shooting experience with up to 10x zoom. Nightography, enhanced with video HDR allows you to capture more brilliant videos — even in dim lighting — and goes further by partnering with popular social apps as well. The night capturing feature is now available in-app on Instagram, so you can take amazing photos at night and message or share them directly from within the app.

You can continue using all the creative and customizable features of Galaxy Z Flip6 without worrying about battery life either, with longer usage time 23 made possible by hardware and software optimization.

Security You Can Trust, Controlled by You

Galaxy Z Fold6 and Flip6 are secured by Samsung Knox , Samsung Galaxy’s defense-grade, multi-layer security platform built to safeguard critical information and protect against vulnerabilities with end-to-end hardware, real-time threat detection and collaborative protection. In the era of AI, Samsung’s commitment to empowering you with choice over your device settings is stronger than ever, which is why you have full control over how you allow your data to enhance AI experiences through Galaxy AI settings. 24 As an added layer of protection, Enhanced Data Protection offers end-to-end encryption when you backup, sync or restore your data with Samsung Cloud. The new Galaxy Z series is also backed by Samsung’s expansive list of security and privacy features including Knox Vault, Security & Privacy Dashboard, Auto Blocker, passkeys, Secure Wi-Fi and Private sharing in Quick Share.

Ongoing Journey to a Sustainable Future

The latest Galaxy Z series reinforces Samsung’s commitment to do more for people and the planet with less by reimagining how mobile technology is designed and packaged. Samsung continues to scale its use of recycled materials with the Galaxy Z Fold6 and Flip6 25 by featuring recycled gold and copper for the first time . 26

Earlier this year, Samsung introduced recycled minerals like cobalt and rare earth elements 27 in the Galaxy S24 series, all of which can be found in components of the Galaxy Z Fold6 and Flip6, along with recycled plastics, aluminum and glass. The Galaxy Z Fold6 and Flip6 also come in a packaging box made from 100% recycled paper material, and they provide seven generations of OS upgrades and seven years of security updates . 28

Galaxy Buds3 Series: Expanding the Connected Experience through Galaxy AI

With the power of Galaxy AI , the Galaxy Buds3 series brings a new communication experience. If you’re attending a class in a foreign language, you can turn on Interpreter 29 in Listening mode on Galaxy Z Fold6 or Flip6 with Galaxy Buds3 series plugged into your ears. This will allow you to hear the lecture translated directly through your Galaxy Buds, removing language barriers that may exist in your studies. Also, simply saying two words through Voice Command 30 allows you to control functions like playing or stopping music without manually touching the earbuds or a connected smartphone. Sound can also be intelligently optimized, regardless of how you wear your Galaxy Buds. The microphones in the Buds3 series analyze both internal and external sound in real time to enhance sound and Active Noise Cancellation (ANC) quality through Adaptive EQ and Adaptive ANC . And if you are listening to music, your Galaxy Buds3 Pro will constantly collect and identify surrounding sound and automatically adjust the optimal level of noise and sound without manual adjustment through Adaptive Noise Control , Siren Detect and Voice Detect , 31 all for your convenience.

Built upon a variety of collected statistical data, the Galaxy Buds3 series comes with a new computational design boasting a comfortable fit. The premium blade design also targets style-centric consumers with an ultra-sleek and modern style complemented with Blade Lights . 32 This new design enables a more intuitive physical experience by allowing you to control the device by simply pinching or swiping up or down on the blade, thereby offering convenience and tasteful aesthetics at the same time. Galaxy Buds3 and Buds3 Pro offer two purpose-built design options. Galaxy Buds3 Pro is Canal Type for those looking for immersive sound, while Buds3 is Open Type for people who prefer to use the device in a variety of situations for an extended period of time.

To deliver a premium audio experience, Galaxy Buds3 Pro is equipped with advanced hardware. Galaxy Buds3 Pro comes with enhanced 2-way speakers with planar tweeter for sophisticated, precise high range sound production, and Dual Amplifiers for a crystal-clear sound experience on the go. And now, thanks to Ultra High Quality 33 Audio that supports a doubled sampling rate with SSC codec, you can listen to a high-resolution audio source as it was intended and enjoy every sound in superb detail. This level of sound quality extends to phone calls, too. With a pre-trained model based on machine learning, the Galaxy Buds3 series is now able to restore the original voice of the speaker in various noise environments while also providing a rich and natural call — similar to the high-quality calls of smartphones — with the Super-Wideband 34 Call feature.

Not only is the Galaxy Buds3 series created to provide the premium audio experience, but it is also designed to do more with less for people and the planet. Galaxy Buds3 and Buds3 Pro feature several components in the cradle and earbuds that use recycled plastics sourced from discarded fishing nets or water barrels. Every Galaxy Buds3 series is packaged in a packaging box made with 100% recycled paper material.

Availability

The Galaxy Z Fold6, Z Flip6 and Galaxy Buds3 series will be available for pre-order starting today, July 10, with general availability starting July 24.

Galaxy Z Fold6 is available in Silver Shadow, Pink and Navy, while Galaxy Z Flip6 is also available in Silver Shadow, Yellow, Blue and Mint color options 35 so you can choose a color that best suits your style. Or order online at Samsung.com and access exclusive Galaxy Z series colors such as Crafted Black, White as well as a Peach color option for Galaxy Z Flip6.

The Galaxy Buds3 series offers an ultra-sleek, modern and comfortable design available in two colors, Silver and White. 36

For your peace of mind, Samsung Care+ 37 — which protects your products with certified care from Samsung experts for accidental damage — will be provided one-year free during pre-order periods.

For more information about Galaxy Z Fold6, Z Flip6, Galaxy Buds3 and Buds3 Pro, please visit: Samsung Newsroom , Samsungmobilepress.com or Samsung.com .

Specifications


		7.6-inch QXGA+* Dynamic AMOLED 2X Infinity Flex Display (2160 x 1856, 20.9:18), 374ppi 120Hz adaptive refresh rate (1~120Hz)

		6.3-inch HD+ Dynamic AMOLED 2X Display (2376 x 968, 22.1:9), 410ppi 120Hz adaptive refresh rate (1~120Hz)

		68.1 x 153.5 x 12.1mm
		.
		132.6 x 153.5 x 5.6mm

		239g
		10MP Selfie Camera F2.2, Pixel size: 1.22μm, FOV: 85˚
		4MP Under Display Camera F1.8, Pixel size: 2.0μm, FOV: 85˚
		12MP Ultra-Wide Camera F2.2, Pixel size: 1.12μm, FOV: 123˚
		50MP Wide-angle Camera Dual Pixel AF, OIS, F1.8, Pixel size: 1.0μm, FOV: 85˚
		10MP Telephoto Camera PDAF, OIS, F2.4, Pixel size: 1.0μm, FOV: 36˚, 3X optical zoom

		Snapdragon 8 Gen 3 Mobile Platform for Galaxy
		Snapdragon is a product of Qualcomm Technologies, Inc. and/or its subsidiaries. Snapdragon is a trademark or registered trademark of Qualcomm Incorporated.
		12GB Memory with 1TB internal storage 12GB Memory with 512GB internal storage 12GB Memory with 256GB internal storage

		4,400mAh (typical) dual battery

		Wired Charging: Up to 50% charge in around 30 min. with 25W Adapter* and 3A USB-C cable* Fast Wireless Charging 2.0 Wireless PowerShare***

		IP48


		5G, LTE, Wi-Fi 6E**, Bluetooth v5.3

		Capacitive Fingerprint sensor (side), Accelerometer, Barometer, Gyro sensor, Geomagnetic sensor, Hall sensor, Proximity sensor, Light sensor
		Samsung Knox with Samsung Knox Vault
		Up to two Nano SIM* and Multi eSIM**

		Silver Shadow, Pink, Navy [Samsung.com Exclusive] Crafted Black, White


		6.7-inch FHD+* Dynamic AMOLED 2X 120Hz Adaptive refresh rate (1~120Hz) Infinity Flex Display (2640 x 1080, 22:9)

		3.4-inch Super AMOLED 60Hz Display* 720 x 748 306 PPI

		71.9 x 85.1 x 14.9mm
		.
		71.9 x 165.1 x 6.9mm

		187g
		10MP Selfie Camera F2.2, Pixel size: 1.22μm, FOV: 85˚
		12MP Ultra-Wide Camera F2.2, Pixel size: 1.12μm, FOV: 123˚
		50MP Wide-angle Camera Dual Pixel AF, OIS, F1.8, Pixel size: 1.0μm, FOV: 85˚
		Snapdragon 8 Gen 3 Mobile Platform for Galaxy
		Snapdragon is a product of Qualcomm Technologies, Inc. and/or its subsidiaries. Snapdragon is a trademark or registered trademark of Qualcomm Incorporated.
		12GB Memory with 512GB internal storage 12GB Memory with 256GB internal storage

		4,000mAh (typical) dual battery

		Wired Charging: Up to 50% charge in around 30min. with 25W Adapter* and 3A USB-C cable* Fast Wireless Charging 2.0 Wireless PowerShare***

		IP48


		5G, LTE, Wi-Fi 6E**, Bluetooth® v5.3

		Capacitive Fingerprint sensor (side), Accelerometer, Barometer, Gyro sensor, Geomagnetic sensor, Hall sensor, Proximity sensor, Light sensor
		Samsung Knox with Samsung Knox Vault
		One Nano SIM* and Multi eSIM**

		Silver Shadow, Yellow, Blue, Mint [Samsung.com Exclusive] Crafted Black, White, Peach


	Silver, White * Available colors may vary by market, carrier or retailer.	Silver, White * Available colors may vary by market, carrier or retailer.
	Earbud: 18.1 x 20.4 x 31.9 mm Charging Case: 58.9 x 48.7 x 24.4 mm	Earbud: 18.1 x 19.8 x 33.2 mm Charging Case: 58.9 x 48.7 x 24.4 mm
	Earbud: 4.7g Charging Case: 46.5g	Earbud: 5.4g Charging Case: 46.5g * with M size eartip
	1-Way: 11mm Dynamic Driver	Enhanced 2-Way: 10.5mm Dynamic + 6.1mm Planar
	3 Mics + VPU	3 Mics + VPU
	UHQ* 24bit Hi-Fi 360 Audio with Direct Multi-Channel* Ultra high quality audio up to 24bit/96kHz is available on Galaxy S24 series, S23 series, Z Fold6, Z Flip6, Z Fold5, Z Flip5 and Tab S9 series with One UI 6.1.1 or above. Additional devices may be supported in the future 24-bit Hi-Fi sound requires Samsung Galaxy devices running OneUI 4.0 or higher and Galaxy Buds3. 24-bit Hi-Fi sound support may vary depending on the application *** Direct Multi-channel is supported with Android One UI version 4.1.1 or later, 360 Audio Supports One UI 3.1 or later	UHQ* 24bit Hi-Fi 360 Audio with Direct Multi-Channel* * Ultra high quality audio up to 24bit/96kHz is available on Galaxy S24 series, S23 series, Z Fold6, Z Flip6, Z Fold5, Z Flip5 and Tab S9 series with One UI 6.1.1 or above. Additional devices may be supported in the future 24-bit Hi-Fi sound requires Samsung Galaxy devices running OneUI 4.0 or higher and Galaxy Buds3 Pro. 24-bit Hi-Fi sound support may vary depending on the application. * Direct Multi-channel is supported with Android One UI version 4.1.1 or later, 360 Audio Supports One UI 3.1 or later.
	ANC	ANC Ambient sound Voice Detect* *** Galaxy Buds3 Pro can distinguish between noise and human voices. When you speak, it switches temporarily to Ambient mode and reduces media volume so that you can hear conversations without taking out your earbuds.
	Earbuds: 48mAh (typical) Charging Case: 515mAh (typical)* * The typical capacity has been tested under third party laboratory conditions. The typical capacity is the estimated average capacity considering the deviation in battery capacity among the battery samples tested under the IEC 61960-3 standard. The rated capacity is 45mAh (earbuds), 500mAh (charging case). Actual battery life may vary depending on the network environment, usage patterns and other factors.	Earbuds: 53mAh (typical) Charging Case: 515mAh (typical)* * The typical capacity has been tested under third party laboratory conditions. The typical capacity is the estimated average capacity considering the deviation in battery capacity among the battery samples tested under the IEC 61960-3 standard. The rated capacity is 50mAh (earbuds), 500mAh (charging case). Actual battery life may vary depending on the network environment, usage patterns and other factors.
	Up to 5 hours / Total up to 24 hours (ANC on) Up to 6 hours / Total up to 30 hours (ANC off)* * Earbuds provide up to 5hrs play time with ANC on (up to 6 hours with ANC off), while the case provides up to 24 hours of battery life (up to 30 hours with ANC off) when the case and earbuds are charged to 100%. Based on internal testing. Audio playback time tested by pairing a pre-production Galaxy Buds3 to a recently released Galaxy smartphone with default settings including ANC off. Actual battery life may vary and depend on usage conditions, settings, number of times charged, Bluetooth signal strength and other factors. Default setting refers to the original setting for the Galaxy Buds3 when it was first released, simply with the power turned on.	Up to 6 hours / Total up to 26 hours (ANC on) Up to 7 hours / Total up to 30 hours (ANC off)* * Earbuds provide up to 6hrs play time with ANC on (up to 7 hours with ANC off), while the case provides up to 26 hours of battery life (up to 30 hours with ANC off) when the case and earbuds are charged to 100%. Based on internal testing. Audio playback time tested by pairing a pre-production Galaxy Buds3 Pro to a recently released Galaxy smartphone with default settings including ANC on. Actual battery life may vary and depend on usage conditions, settings, number of times charged, Bluetooth signal strength and other factors. Default setting refers to the original setting for the Galaxy Buds3 Pro when it was first released, simply with the power turned on.
	Up to 3.5 hours / Total up to 18h (ANC on) Up to 4 hours / Total up to 20h (ANC off) * Earbuds provide up to 3.5hrs voice call time with ANC on (up to 4 hours with ANC off), while the case provides up to 18 hours of battery life (up to 20 hours with ANC off) when the case and earbuds are charged to 100%. Based on internal testing. Voice call time tested by pairing pre-production Galaxy Buds3 to a recently released Galaxy smartphone with default settings including ANC off. Actual battery life may vary and depend on usage conditions, settings, number of times charged, Bluetooth signal strength and other factors.	Up to 4.5 hours / Total up to 20h (ANC on) Up to 5 hours / Total up to 22h (ANC off) * Earbuds provide up to 4.5hrs voice call time with ANC on (up to 5 hours with ANC off), while the case provides up to 20 hours of battery life (up to 22 hours with ANC off) when the case and earbuds are charged to 100%. Based on internal testing. Voice call time tested by pairing pre-production Galaxy Buds3 Pro to a recently released Galaxy smartphone with default settings including ANC on. Actual battery life may vary and depend on usage conditions, settings, number of times charged, Bluetooth signal strength and other factors.
	Bluetooth® 5.4, Auto Switch AAC, SBC	Bluetooth® 5.4, Auto Switch AAC, SBC
	Voice Pickup Unit (VPU), Force & Touch (Swipe), SWIR, Accelerometer, Hall sensor	Voice Pickup Unit (VPU), Force & Touch (Swipe), SWIR, Accelerometer, Hall sensor
	Android 10 or higher with more than 1.5GB of Memory * Some features may not be available on non-Samsung devices. Availability may vary by market, operator or connected device.	Android 10 or higher with more than 1.5GB of Memory * Some features may not be available on non-Samsung devices. Availability may vary by market, operator or connected device.
	IP57* * earbuds only	IP57* * earbuds only

1 Samsung Account login may be required to use certain Samsung AI features. Samsung does not make any promises, assurances or guarantees as to the accuracy, completeness or reliability of the output provided by AI features. Availability of Galaxy AI features may vary depending on the region/country, OS/One UI version, device model and phone carrier. Some function availability may vary by device model. Galaxy AI service may be limited for minors in certain regions with age restrictions over AI usage. Galaxy AI features will be provided for free until the end of 2025 on supported Samsung Galaxy devices. Different terms may apply for AI features provided by third parties. 2 Enhanced Armor Aluminum is incorporated into frame and hinge housing of the device. Armor Aluminum Frame does not include volume and side keys. 3 Corning® Gorilla® Glass Victus®2 is incorporated into front and rear of the device. 4 Snapdragon is a trademark or registered trademark of Qualcomm Incorporated. Snapdragon branded products are products of Qualcomm Technologies, Inc. and/or its subsidiaries. 5 Features for Note Assist require a network connection and Samsung Account login. Service availability may vary by language. Voice recording feature in the Samsung Notes app may not be supported in some countries. Summarizing feature is activated when a certain number of characters is met and is under the character limit. Audio files must be under 3 hours in duration to be processed. Accuracy of results is not guaranteed. 6 Overlay translation not supported for PDF files secured with password. 7 Composer requires a network connection and Samsung Account login. Service availability may vary by language. Accuracy of results is not guaranteed. 8 S Pen sold separately. 9 Sketch to image requires a network connection and Samsung Account login. Editing with Sketch to Image may result in a resized photo up to 12MP. A visible watermark is overlaid on the image output upon saving in order to indicate that the image is generated by AI. The accuracy and reliability of the generated output is not guaranteed. 10 Google Gemini app requires Google Account login. Product functionality may be dependent on app and device settings. Some functions may not be compatible with certain apps. Service availability may vary by country, language and device model. Accuracy of results is not guaranteed. 11 Sequences shortened and simulated. Results for illustrative purposes only. Results may vary depending on visual matches. Requires internet connection. Users may need to update Android to the latest version. Product functionality may be dependent on your app and device settings. Some functions may not be compatible with certain apps. Availability of the service varies by country and language. Accuracy of results is not guaranteed. Circle to Search is not available via the FlexWindow. 12 Interpreter requires Samsung Account login. Certain languages may require language pack download. Service availability may vary by language. Accuracy of results is not guaranteed. Availability and supported features may vary by country, region or carrier. Availability of supported languages may vary. 13 Live Translate requires a network connection and Samsung Account login. Live Translate is only available on the pre-installed Samsung Phone apps and some third-party apps. Support may vary by region. Certain languages may require language pack download. Service availability may vary by language. Accuracy of results is not guaranteed. 14 Features for Photo Assist require a network connection and Samsung Account login. Editing with Generative Edit results in a resized photo up to 12MP. A visible watermark is overlaid on the image output upon saving in order to indicate that the image is generated by AI. The accuracy and reliability of the generated output is not guaranteed. 15 Portrait Studio requires a network connection and Samsung Account login. Supports JPG, HEIC (HEIF), BMP and PNG files. The background must not be transparent. Editing with Generative Portrait results in a resized photo up to 12MP. A visible watermark is overlaid on the image output upon saving in order to indicate that the image is generated by AI. The accuracy and reliability of the generated output is not guaranteed. 16 Instant Slow-mo feature is available on Samsung Video Player and Samsung Gallery. May not be available on certain video file types. Accuracy of results not guaranteed. 17 Measured diagonally, Galaxy Z Flip6’s Main Screen size is 6.7-inch in the full rectangle and 6.6-inch when accounting for the rounded corners; actual viewable area is less due to the rounded corners and camera hole. 18 Measured diagonally, Galaxy Z Flip6’s Cover Screen is 3.4-inch in the full rectangular form; actual viewable area is approximately 95% of the full rectangular area due to the rounded corners and lower cutout. Galaxy Z Flip6’s Cover is equipped with a proximity sensor and supports HBM. Galaxy Z Flip6’s Cover Screen HBM has a peak brightness of 1,600nits for a brighter and clearer display. 19 Suggested Replies feature for Chat Assist requires network connection to receive messages. It can suggest replies with or without network connection once the messages are received by the device. Samsung Account login required. Only supported from the FlexWindow of Galaxy Z Flip6. Service availability may vary by language and app. Accuracy of results is not guaranteed. 20 Samsung Health requires a network connection and Samsung Health login. Availability of Samsung Health may vary depending on country. Supported items may vary by country. 21 Photo Ambient requires a network connection and Samsung Account login. Reflection of real-time weather conditions may be delayed as service relies on local weather information updates. Certain indoor, nighttime and low-resolution photos may not be compatible. The accuracy and reliability of the generated output is not guaranteed. Service is currently only available on Galaxy S24 series, Z Flip6 and Fold6. 22 Auto Zoom is limited in low-light conditions. Auto Zoom mode will disengage if the zoom is manually adjusted or if switched between front and back camera. 23 Actual battery life varies by network environment, features and apps used, frequency of calls and messages, the number of times charged and many other factors. 24 Samsung Account login required. Galaxy AI settings preventing server access will limit the functionality of some AI features. Regardless of server access, Samsung does not save user input or output data. 25 For more information about the recycled materials in the latest Galaxy Z series, as well as other Galaxy devices, please review the product environmental reports located on the Samsung Sustainability website . 26 The gold bonding wires in certain camera modules of Galaxy Z Fold6 and Flip6 are made with 100% recycled gold sourced from e-waste and gold scraps. In addition, the copper foils of main logic boards and select FPCBs are designed with 100% recycled copper sourced from discarded copper wires and chips. The above measurements are based on weight. 27 Neodymium 28 Galaxy Z Fold6 and Flip6 will be supported with seven generations of OS upgrades and seven years of security updates from the global launch date. 29 Audio interpretation is only available when wearing Buds and connected to a Samsung Galaxy smartphone. Interpreter feature is not directly provided by Buds themselves. If Buds are unavailable, the interpreted content is provided on the screen of your Samsung Galaxy smartphone. Certain languages may require language pack download. Service availability may vary by language, country, region or carrier. Samsung Galaxy devices may require the latest software update to properly support Galaxy AI features. 30 Language Setting follows the system language setting. Voice Command menu appears when language pack same as system language exists. Supporting Language at the time of launch includes Korean and US English, and the supporting language will be expanded further. 31 Adaptive Noise Control, Voice Detect and Siren Detect features are only available on Samsung Galaxy Buds3Pro. Adaptive Noise Control, Voice Detect and Siren Detect are all off by default.. 32 Blade Lights only available on Samsung Galaxy Buds3 Pro. 33 Ultra-high quality audio up to 24bit/96kHz’ is available on Galaxy S24 series, S23 series, Z Fold6, Z Flip6, Z Fold5, Z Flip5 and Tab S9 series with One UI 6.1.1 or above. Ultra-high quality audio feature is only available on select Samsung Galaxy devices at this time. Additional devices may be supported in the future. 34 Super-Wideband call feature allow Buds to transmit voice up to 16kHz, while previous BT earphones only transmit up to the 8kHz band. 35 Availability of color for Galaxy Z series may vary by market, region or carrier. 36 Availability of color for Galaxy Buds3 series may vary by market, region or carrier. 37 Terms and conditions apply. Samsung Care+ coverage, service type and promotion details may vary by country/region and deductible (service fee) may apply. To be eligible for Samsung Care+ promotion benefit, registration may be required. For detailed Samsung Care+ information, please visit https://www.samsung.com/samsung-care-plus/

TAGS Galaxy AI Galaxy Buds3 Galaxy Buds3 Pro Galaxy Unpacked Galaxy Unpacked 2024 Galaxy Z Flip6 Galaxy Z Fold6

Products > Mobile

Press Resources > Press Release

Samsung-Mobile-Galaxy-Unpacked-2024-Galaxy-Z-Fold6-and-Z-Flip6-Official-press-release_dl1.jpg

Samsung-Mobile-Galaxy-Unpacked-2024-Galaxy-Z-Fold6-and-Z-Flip6-Official-press-release_dl2.jpg

Samsung-Mobile-Galaxy-Unpacked-2024-Galaxy-Z-Fold6-and-Z-Flip6-Official-press-release_dl3.jpg

Samsung-Mobile-Galaxy-Unpacked-2024-Galaxy-Z-Fold6-and-Z-Flip6-Official-press-release_dl4.jpg

Samsung-Mobile-Galaxy-Unpacked-2024-Galaxy-Z-Fold6-and-Z-Flip6-Official-press-release_dl5.jpg

Samsung-Mobile-Galaxy-Unpacked-2024-Galaxy-Z-Fold6-and-Z-Flip6-Official-press-release_dl6.jpg

Samsung’s Expanded Wearables Portfolio Unlocks Intelligent Health Experiences for All
[Video] Galaxy AI: A Personal Real-Time Interpreter That Writes Emails and Crafts Messages on the Fly — New Ways To Communicate
[Video] Adjust Angles From a Distance, Capture Even the Smallest Details — New Ways To Create
[Video] Maximize Efficiency and Imagination With Galaxy AI — New Ways To Get Things Done
[Video] A Personal Smart Health Assistant — New Ways To Manage Health

For any issues related to customer service, please go to Customer Support page for assistance. For media inquiries, please click Media Contact to move to the form.

Get daily updates from Samsung Newsroom

Media Contact
SAMSUNG.COM
Terms of Use
Privacy and Cookies

People & Culture
More stories
TVs & Displays
Home Appliances
Network Solutions
Semiconductors
More Products
Citizenship
Environments
Sustainability

More From Forbes

How BCG Is Revolutionizing Consulting With AI: A Case Study

Share to Facebook
Share to Twitter
Share to Linkedin

In a world where AI is transforming every sector, companies are constantly seeking ways to gain a competitive edge. Boston Consulting Group (BCG) is leading the charge by embracing artificial intelligence (AI), particularly generative AI, to revolutionize its internal operations and consulting services. Let’s delve into how BCG is leveraging AI to transform its business processes and the consulting industry as a whole.

The Strategic Importance Of AI At BCG

AI is not just a buzzword at BCG; it is a fundamental element of their strategy. Vlad Lukic, Managing Director and Senior Partner at BCG, emphasizes the significance of AI, stating, "It gets into the crux of our business, right? And it's going to be fundamental to the toolkit and skills that we need to have." AI serves as an assistant, enabling BCG consultants to operate at unprecedented speeds, thus allowing them to generate insights faster and drive impactful results for their clients.

Real-World Applications Of AI At BCG

1. Interview Processing and Analysis:

Lukic recalls his summer internship, where he had to interview 30 engineers about materials science over three days, transcribe the conversations, distill the insights, and create slides. This labor-intensive process took two weeks. In contrast, a recent consultant used BCG's enterprise GPT to perform a similar task. "On the third day, he had slides and insights ready to go," Lukic marvels. The AI tool transcribed interviews, highlighted key themes, and generated draft presentations in minutes, reducing a two-week process to two or three days.

Best High-Yield Savings Accounts Of 2024

Best 5% interest savings accounts of 2024.

2. Gene: BCG's Innovative Conversational AI:

Another striking example of AI's impact at BCG is the development of Gene, a conversational AI designed to engage with humans and create audio experiences. Originally conceived as a co-host for BCG's "Imagine This" podcast about the future, Gene has evolved into a versatile tool for client engagement and content creation.

Paul Michelman, editor-in-chief at BCG, explains, "Gene was born for a specific job, really one job, and its original training was to be a co-host of a podcast." However, the potential of Gene quickly became apparent, and its applications have expanded. Gene now appears at live events with clients and other audiences, engaging in conversations about the future of AI and thought leadership.

Enterprise GPT: A Game Changer

BCG's enterprise GPT is a cornerstone of their AI strategy. Rolled out to every employee, this tool ensures all data remains within BCG's control. Consultants can also build their own GPTs for specific engagements, fostering innovation and efficiency. Over 3,000 GPTs have been created, addressing tasks from document summarization to administrative functions. Lukic highlights its impact on productivity, noting, "It's really helping us move to a different level of speed."

Evolving Roles And Skills In The AI Era

With AI taking over routine tasks, the role of consultants is evolving. Lukic underscores the need for purposeful toil and sanity checks to ensure junior consultants develop essential skills. He explains, "We are forcing some of those conversations with our team members, so that we can build their skills along the way." This includes teaching consultants how to engage with AI tools effectively, ensuring they can provide accurate and reliable insights.

The development of Gene has also prompted new considerations in AI deployment. Bill Moore from BCG Design Studios, who created Gene, explains the challenges in balancing autonomy and control: "We adjust, we work with the temperature to keep that sort of fine-tuned and we'll drop it down to zero if we need really accurate responses."

Measuring The Impact Of AI

BCG conducted a scientific experiment involving 750 employees to measure the impact of generative AI on performance and efficiency. The results were compelling. For straightforward tasks, productivity increased by 30-40% for new hires and 20-30% for experienced consultants. However, for complex tasks, productivity sometimes decreased due to the challenges of debugging AI-generated outputs. This experiment highlighted the importance of understanding where AI can be most effective and implementing proper guardrails to ensure accuracy.

Insights From BCG's GenAI Experiment

BCG's broader research into generative AI reveals significant insights into its value and potential pitfalls. The study found that around 90% of participants improved their performance when using GenAI for creative ideation. However, when applied to business problem-solving—a task outside the tool's current competence—many participants trusted misleading outputs, resulting in a 23% decline in performance compared to those who didn't use the tool. This underscores the necessity of proper training and understanding the limitations of AI tools.

Ensuring Accuracy And Mitigating Risks

To mitigate risks associated with AI, BCG has implemented several guardrails. Human experts review AI-generated insights, and workflows are designed to ensure continuous oversight. Additionally, BCG fine-tunes their models based on usage and feedback, reducing the likelihood of errors.

In the case of Gene, transparency and ethical considerations are paramount. Paul Michelman emphasizes, "We think it's very important... to be fully clear when we're using technology. And two, to really avoid anthropomorphizing." This approach extends to Gene's voice, which is intentionally androgynous and slightly robotic to clearly differentiate it from a human.

Governance And Strategic Implementation Of AI

BCG employs a dual approach to AI implementation. While top-down initiatives identify key workflows that can benefit from AI, grassroots innovation is also encouraged. A senior task force focuses on internal support functions and consulting cohorts, identifying where AI can eliminate bottlenecks and enhance productivity.

The Future Of Consulting In The AI Era

Looking ahead, AI is poised to reshape the consulting industry. Lukic predicts that within a decade, 50% of current tasks will be automated through AI, allowing consultants to focus more on change management and driving adoption within client organizations.

Bill Moore envisions a future where conversational interfaces like Gene become a new layer of interaction with technology, potentially revolutionizing accessibility and user experience.

Strategies For Successful AI Adoption

For CEOs considering AI adoption, Lukic offers two key pieces of advice. First, don't wait. Start addressing frictions and building the necessary governance structures now. Second, engage the organization. Avoid outsourcing AI implementation entirely and instead, focus on building internal capabilities.

Transforming Consulting With AI

BCG's strategic application of AI, particularly generative AI and conversational AI like Gene, showcases how embracing technology can revolutionize internal processes and enhance client service. By leveraging AI tools like enterprise GPT and Gene, BCG is boosting productivity, fostering innovation, and preparing its workforce for the future. As AI continues to evolve, BCG's proactive approach provides a valuable blueprint for other organizations aiming to harness the power of AI in their own operations.

Editorial Standards
Reprints & Permissions

Join The Conversation

One Community. Many Voices. Create a free account to share your thoughts.

Forbes Community Guidelines

Our community is about connecting people through open and thoughtful conversations. We want our readers to share their views and exchange ideas and facts in a safe space.

In order to do so, please follow the posting rules in our site's Terms of Service. We've summarized some of those key rules below. Simply put, keep it civil.

Your post will be rejected if we notice that it seems to contain:

False or intentionally out-of-context or misleading information
Insults, profanity, incoherent, obscene or inflammatory language or threats of any kind
Attacks on the identity of other commenters or the article's author
Content that otherwise violates our site's terms.

User accounts will be blocked if we notice or believe that users are engaged in:

Continuous attempts to re-post comments that have been previously moderated/rejected
Racist, sexist, homophobic or other discriminatory comments
Attempts or tactics that put the site security at risk
Actions that otherwise violate our site's terms.

So, how can you be a power user?

Stay on topic and share your insights
Feel free to be clear and thoughtful to get your point across
‘Like’ or ‘Dislike’ to show your point of view.
Protect your community.
Use the report tool to alert us when someone breaks the rules.

Thanks for reading our community guidelines. Please read the full list of posting rules found in our site's Terms of Service.

Camel integration quarterly digest: Q2 2024

Welcome to our second edition of Red Hat’s quarterly newsletter all about Apache Camel! This series aims to share all noteworthy Camel goodness over the last quarter so you don’t miss a thing! Be sure to read the previous edition to catch up on all the exciting updates and insights in Q1 2024.

Red Hat build of Apache Camel 4.4

Red Hat build of Apache Camel 4.4 introduced several new features and enhancements, including support for JDK 21, newly supported components like Jasypt security and Splunk, and new tools such as Kaoto visual designer and HawtIO diagnostic console. It offers modernized integration capabilities, streamlined data management with the "Variables" feature, and extended support for new environments including Quarkus 3.8, Spring Boot 3.2 and new architectures like IBM Power and IBM Z. Additionally, it facilitates easier migrations from Red Hat Fuse using new supporting resources.

For more details, visit the What’s new in Red Hat build of Apache Camel 4.4 article.

Red Fuse 7 Extended Lifecycle Phase

Red Hat Fuse 7 (based on Apache Camel 2) has entered the Extended Lifecycle Support (ELS) phase , requiring an ELS subscription in addition to the base product subscription. During the ELS-1 phase, which lasts two years following the end of Maintenance Support, Red Hat will provide Critical impact security fixes and selected urgent-priority bug fixes as they become available. Proactive delivery of Critical impact security fixes will continue independently of customer requests. The most recent version, Fuse 7.13, was released on May 23rd.

Red Hat recommends transitioning to the Red Hat build of Apache Camel 4. This new version offers new and enhanced features and greater support for modern integration needs. For detailed guidance, you can start on the Fuse to Camel migration page .

A new way forward for Camel on OpenShift

For over six years, Camel K has led the way in cloud-native, low-code, and managed integration services. Many of its features are now part of Camel Core, benefiting all Camel users with cloud-native capabilities. This shift allows us to provide a more stable and innovative environment by focusing on the mature cloud-native features in Camel Core. Our efforts lead us towards the one solution for all existing and new customers needing enterprise integration in the hybrid cloud; the Red Hat build of Apache Camel 4.

For more details, read the recent announcement of Red Hat Camel K End of Life Notice and stay tuned for more updates and resources to assist with transition from Camel K to Red Hat build of Apache Camel 4.

Dive into the latest developments within Apache Camel 4 through our curated selection of articles.

Implement AI-driven edge to core data pipelines Bruno Meseguer presented a new solution pattern describing how to enhance real-time decision-making with AI-driven edge to core data pipelines. Learn to preprocess data at the edge, securely transmit it, and integrate AI models at the core using Red Hat OpenShift AI, Red Hat build of Apache Camel and Red Hat streams for Apache Kafka.

Configure SOAP web services with Apache Camel on Quarkus Luis Falero Otiniano explained the complete walkthrough of setting up a Camel Quarkus project and creating REST-to-SOAP integration routes, enabling efficient integration of SOAP web services in Quarkus applications

Feeding LLMs efficiently: data ingestion to vector databases with Apache Camel Zineb Bendhiba explored how to set up a pipeline for managing and processing vast amounts of data to optimize LLM performance. It covers integrating Apache Camel with vector databases for effective data retrieval and indexing.

Kaoto release v2.0 and Kaoto release v2.1 Ricardo Martinez announced new releases of Kaoto 2.x which focuses on low-code development of Apache Camel integrations in Visual Studio Code and Red Hat OpenShift Dev Spaces.

Build an extendable multichannel messaging platform Bruno Meseguer introduced a new solution pattern integrating multiple communication channels and services, ensuring efficient message handling and delivery.

Event-driven API Management Abdelhamid Soliman outlined an architecture which pushes internal events from an event broker (Kafka) to API consumers, allowing to manage events as an API product by applying API management practices to an event-driven API product. Apache Camel is used in Webhook delivery system as webhook creator, dispatcher, 3scale custom HMAC policy and order event simulator.

Demos and Presentations

See Apache Camel 4 in action in the following demos and presentations:

On-demand webinar - Optimizing Enterprise Integration Strategies in a World of the Hybrid Cloud by Mike Ward, Ivo Bek and Otavio Piske
UPS's Journey to OpenShift with Red Hat Integration by Will Chang and Alex Pomponio at Red Hat Summit 2024
Quickly run Camel JBang with Spring Boot or Quarkus (community, v4.6) by Claus Ibsen
Kaoto 2.0 Introduction by Ricardo Martinez
Quickly run Apache Camel and Kafka locally using Docker Compose and test for failover by Claus Ibsen
Quarkus meets AI : Build your own LLM-powered application by Zineb Bendhiba and Dimitris Andreadis
Try OpenShift AI and integrate with Apache Camel by Bruno Meseguer

You may meet us at the upcoming conferences:

17-19th WeAreDevelopers in Berlin
Doing integration in easiest and cheapest way by Zheng Feng and Vicky Wu
7-11th Devoxx Belgium
21-24th IBM TechXchange in Vegas
2-4th Devoxx Morocco in Marrakech
12-15th KubeCon NA & BackstageCon in Salt Lake City
4-5th Open Source Experience in Paris
Red Hat Enterprise Linux
Red Hat OpenShift
Red Hat Ansible Automation Platform
See all products
See all technologies
Developer Sandbox
Developer Tools
Interactive Tutorials
API Catalog
Operators Marketplace
Learning Resources
Cheat Sheets

Communicate

Contact sales
Find a partner

Report a website issue

Site Status Dashboard
Report a security problem

RED HAT DEVELOPER

Build here. Go anywhere.

We serve the builders. The problem solvers who create careers with code.

Join us if you’re a developer, software engineer, web designer, front-end designer, UX designer, computer scientist, architect, tester, product manager, project manager or team lead.

IMAGES

Instant
The Top 5 AI Presentation Makers for 2023: A Comparison
Revolutionize Your Presentations with Sendsteps: AI & PPT Maker
creating presentations with ai
9 Best AI Presentation Software And Tools In 2023
9 Best AI Presentation Software And Tools In 2023

VIDEO

How to Generate Ai Slides Presentation ft. PopAi
5 AI Websites to Boost Productivity #productivity #ai #websites
Create presentations, Websites and Documents with AI (Gama)
Powerpresent AI
Top AI Websites You Must Visit!
How to use Gamma App for Creating AI Generated Slides for Free

COMMENTS

Free AI presentation maker
AI presentation maker. When lack of inspiration or time constraints are something you're worried about, it's a good idea to seek help. Slidesgo comes to the rescue with its latest functionality—the AI presentation maker! With a few clicks, you'll have wonderful slideshows that suit your own needs. And it's totally free!
Free online AI Presentation Maker
‍Free AI Presentation Maker for Stunning Decks . Create professional, stunning presentations in minutes. Generate ready-to-use presentations from just a text prompt. Get Started for Free. Top companies and cool startups, they're all jazzed about our AI PPT Maker. ...
Presentations.AI
Create stunning PowerPoint presentations in seconds with Presentations.AI - the ultimate AI presentation maker. Just type your idea and watch as we craft a professional PPT for you. Perfect for all: businesses, educators, and hobbyists. Dive in now, start for free!
Gamma
Create unlimited presentations, websites, and more—in seconds. Everything you need to quickly create and refine content with advanced AI. Gamma allows me to package up information in ways I can't with slides, while still creating good flow for my presentations. Ann Marie, Director of Product at Koalafi.
10 Best AI Presentation Generators (July 2024)
Visit Beautiful.ai →. 4. Slidebean. Slidebean is a web-based presentation tool that revolutionizes the way presentations are made. With just a few clicks, users can create powerful presentations that leave a lasting impression. The beauty of Slidebean lies in its ability to separate content creation from slide design.
Free Online AI Presentation Maker
Visme AI Presentation Maker generates presentations for any purpose: choose a style that fits your subject and taste the most and remember - the more accurate the prompt, the better the result. Ready-to-use presentations in minutes. Starting is often the hardest part of a project. Visme's free AI presentation maker helps you overcome this ...
The first presentation maker with design AI
The first presentation maker with design AI. Create professional, stunning presentations in minutes. Beautiful.ai has hundreds of smart slides built with AI-assisted design, so you can present ideas meaningfully, easily, and without putting other work on hold. Get Started. How it works.
AI Powerpoint
Create a working presentation or document you can refine and customize in under a minute. Sign up for free and turn your ideas into life with Gamma. Gamma allows me to package up information in ways I can't with slides, while still creating good flow for my presentations. A new medium for presenting ideas, powered by AI.
DesignerBot: Your Personal AI Presentation Maker
Meet your AI presentation maker. Get the power of generative AI right inside your Beautiful.ai workspace. DesignerBot is a powerful creative partner that designs slides quickly, helps brainstorm ideas and generates text and images in a snap. All you have to do is ask, and watch DesignerBot generate a unique deck for you in seconds.
15 Best AI Presentation Makers in 2024 [Free & Paid]
Plus is an innovative AI presentation maker that integrates artificial intelligence to simplify the presentation creation process. The tool makes it easy for individuals or businesses to generate AI presentations or edit slides with AI. What makes Plus special is that it has seamless integrations between Google Slides and PowerPoint. Features
Free AI presentation maker
Generate a beautiful presentation in seconds, with Pitch's AI generator. Enter a prompt, select a color palette and font, then endlessly edit and adapt your AI-generated presentation with your team.
AI Presentation Maker
Say hello to Fliki AI Presentation Maker, your ultimate solution for creating professional presentations in no time. Our AI powerpoint generator empowers you to input your presentation idea and let AI do the heavy lifting. With AI-generated templates, premium stock media, and advanced features, you can transform your ideas into captivating ...
AI Presentation Maker
Experience seamless presentation creation with SlidesPilot's AI Presentation Maker, your AI-Driven PowerPoint Copilot. Harness cutting-edge AI to design, structure, and refine PowerPoint slides with ease. Ideal for innovators, educators, and anyone looking to elevate their presentation game with smart technology. Dive into the future of presentations today.
12 Best AI Tools for Presentations in 2024
Tools for creating documents and web pages along with presentations; Designs.ai. Great for: Fully loaded AI tools. Paid plan starts at: $29/month. Designs.ai offers an AI-powered presentation builder that can help you with the entire process, from outlining to creating professional decks. But they also offer many other AI tools like image and ...
10 Best AI Tools for Presentations in 2024
10 Best AI Presentation Tools 2024. 1. Beautiful.ai. Via Beautiful.ai. Beautiful.ai is an innovative AI presentation maker that aims to revolutionize how you create engaging presentations. The platform makes smart design recommendations through its intuitive interface and streamlines the creation process.
AI Presentation Generator
Discover SlidesPilot's comprehensive AI Presentation Suite for business and education, including AI Presentation Maker, PowerPoint Image Generator, and easy conversions from PDF and Word to PPT. Enhance your presentations with smart, AI-driven tools that simplify slide creation across any topic. Dive into a vast collection of free PowerPoint templates and Google Slides Themes, all designed to ...
Free AI presentation maker: generate slides in seconds
Try the AI Menti Builder today! This is the first version of the AI Menti Builder, and we are committed to continually enhancing our AI-generated content to ensure it becomes more accurate. Try it out and let us know what you think! Add a prompt and watch as it instantly crafts an interactive draft of a presentation, fully customizable by you.
Beautiful.ai
Virtually every presentation tool you need. As a presentation tool made by designers but geared towards everyone, Beautiful.ai comes fully loaded with dozens of essential presentation creation tools as well as many you didn't even know you needed. Your only limit will be your imagination. View All Templates.
SlideSpeak
Our ChatGPT-powered platform will generate highly accurate summaries for you. Use our AI to create presentations for you. Simply upload a document and ask SlideSpeak to generate a presentation based on the content. Our AI understands the content of all documents you've uploaded. Simply ask questions, request summaries and much more.
AI Presentation Generator
AI-Designed Templates for Every Theme. Our AI Presentation Generator stands out with its array of AI-designed templates, ensuring each presentation is not only content-rich but also visually striking. AI-generated images are closely related to the topic and contents of your presentations, offering a perfect blend of design and relevance.
Presentations and videos with engaging visuals for hybrid teams
Prezi AI is your new creative partner. Save time, amplify your ideas, and elevate your presentations. ... Prezi has been a trusted presentation partner for over 15 years. 180+ countries. 140,000,000+ 140M+ people who ️ Prezi. 25%. more effective than slides* 40%. more memorable* *independent Harvard study of Prezi vs. PowerPoint See why our ...
Free AI Presentation Generator
Venngage's free AI presentation generator is designed to help you overcome this initial hurdle by quickly delivering a solid first draft. Within minutes, you'll have a ready-to-use presentation that requires minimal customization, yet is fully editable for further creative edits when needed. Although AI sets a strong foundation, it can't ...
Gamma: How to Use It to Teach
Gamma is an AI-powered presentation generator that can output in slides, documents, or webpages with very little input required beyond a written request. Crucially, this tool can use AI to ...
AI Presentation Maker
Create a working presentation or document you can refine and customize in under a minute. Sign up for free and turn your ideas into life with Gamma. Gamma allows me to package up information in ways I can't with slides, while still creating good flow for my presentations. A new medium for presenting ideas, powered by AI.
Samsung Galaxy Z Fold6 and Z Flip6 Elevate Galaxy AI to New Heights
Earlier this year, Samsung ushered in the era of mobile AI through the power of Galaxy AI. 1 With the introduction of the new Galaxy Z series, Samsung is opening the next chapter of Galaxy AI by leveraging its most versatile and flexible form factor perfectly designed to enable a range of unique mobile experiences. Whether using Galaxy Z Fold ...
How BCG Is Revolutionizing Consulting With AI: A Case Study
The AI tool transcribed interviews, highlighted key themes, and generated draft presentations in minutes, reducing a two-week process to two or three days. ... Transforming Consulting With AI.
Illustrator on the web (beta) overview
Illustrator on the web (beta) FAQ; Troubleshooting issues FAQ; Keyboard shortcuts for Illustrator on the web (beta) Create and combine shapes on the web; Add and edit text on the web; Apply colors and gradients on the web; Draw and edit paths on the web; Work with cloud documents on the web; Invite collaborators to edit on the web; Illustrator ...
Camel integration quarterly digest: Q2 2024
Demos and Presentations. See Apache Camel 4 in action in the following demos and presentations: On-demand webinar - Optimizing Enterprise Integration Strategies in a World of the Hybrid Cloud by Mike Ward, Ivo Bek and Otavio Piske; UPS's Journey to OpenShift with Red Hat Integration by Will Chang and Alex Pomponio at Red Hat Summit 2024

stop bullying

welcome back

business pitch

Create your presentation Create personalized presentation content

Generate presentations in minutes

Customize your AI-generated presentation online

How does it work?

Choose your preferred style and tone

Make any desired changes

Download the final result for free

The World's Best AI Presentation Maker

Key features of our AI presentation maker

Effortless Creation

Personalized Design

Anti-fragile Templates

PowerPoint Compatibility

Seamless Sharing

Analytics &Tracking

Multi-device Compatibility

Multilingual Support

Idea to Deck in seconds

Creative power that goes way beyond templates

Brand consistent

Presentations.AI is simple, fast and fun

Bring your ideas to life instantly

You bring the story. We bring design.

A collaborative AI partner at your command

Create at the speed of thought.

10 Best AI Presentation Generators (July 2024)

Table Of Contents

2. Slides AI

3. Beautiful.ai

4. Slidebean

6. Synthesia

7. Simplified

8. Sendsteps

You may like

Recent Posts

15 Best AI Presentation Makers in 2024 [Free & Paid]

Table of Contents

Visme’s AI-Powered Tools

Rich Library of Templates and Styles

Array of Customization Options

Extensive Library of Stock Photos/ AI Image Generator

Audio and Voiceover

Data Visualization

Animations and Interactive Elements

Animated 3D Graphics and Illustrations

Collaboration

Presenter Studio

Download and Sharing Options

2. Slidesgo

3. Beautiful.ai

4. Storydoc

6. Design.AI

7. Simplified

9. Sendsteps

10. Decktopus

13. Appy Pie

14. Wonderslide

15. SlidesAI

AI Document Generator

Brand Wizard

Visme AI Edit Tools

Visme AI Text Generator

Visme’s AI Image Generators

Easily Tap into the Power of AI with Visme

Create stunning presentations in minutes with Visme

Recommended content for you:

Effortless Design Content in Minutes with the AI Design Generator

About the Author

AI Presentation Maker

Magic Create

Stock Media

How to create a presentation in 3 simple steps

Customize your presentation

Download your presentation

Loved by content creators around the world

$95+ million

Excellent Neural Voices + Super Fast App