- Texas Go Math
- Big Ideas Math
- enVision Math
- EngageNY Math
- McGraw Hill My Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy


Go Math Grade 5 Chapter 11 Answer Key Pdf Geometry and Volume
Go Math Grade 5 Chapter 11 Answer Key Pdf: Go Math Grade 5 Answer Key Chapter 11 Geometry and Volume contains the 5th standard solutions with brief explanations which helps the students to gain the highest marks in the exams. This chapter contains the concepts of Geometry and volume of rectangular prisms. We provide the Go Math Grade 5 Answer Key in such a way that the students will never feel difficulty in learning the geometry and volume.
Geometry and Volume Go Math Grade 5 Chapter 11 Answer Key Pdf
Every student has a chance to know how to find out the Geometry and Volume and how to find out the volume of shapes with the Go Math Grade 5 Key. Get quick solutions with Go Math Answer Key. Get the solutions to this chapter topic wise. Go through the topics mentioned below and start your preparation. The concepts in this chapter include polygons, triangles, quadrilaterals, estimate volume, understand volume, the volume of the rectangular prism
Lesson 1: Polygons
Share and Show – Lesson 1: Polygons – Page No. 639
Problem solving – lesson 1: polygons – page no. 640.
Lesson 2: Triangles
Share and Show – Lesson 2: Triangles – Page No. 645
Problem solving – lesson 2: triangles – page no. 646.
Lesson 3: Quadrilaterals
Share and Show – Lesson 3: Quadrilaterals – Page No. 651
Problem solving – lesson 3: quadrilaterals – page no. 652.
Lesson 4: Properties of Two-Dimensional Figures
Share and Show – Lesson 4: Properties of Two-Dimensional Figures – Page No. 455
On your own – lesson 4: properties of two-dimensional figures – page no. 456, share and show – lesson 4: properties of two-dimensional figures – page no. 656, problem solving – lesson 4: properties of two-dimensional figures – page no. 657.
Mid-Chapter Checkpoint
Mid-Chapter Review – Vocabulary – Page No. 661
Mid-chapter review – page no. 662.
Lesson 5: Unit Cubes and Solid Figures
Share and Show – Lesson 5: Unit Cubes and Solid Figures – Page No. 665
Lesson 5: unit cubes and solid figures – page no. 666.
Lesson 6: Understand Volume
Share and Show – Lesson 6: Understand Volume – Page No. 671
Problem solving – lesson 6: understand volume – page no. 672.
Lesson 7: Estimate Volume
Share and Show – Lesson 7: Estimate Volume – Page No. 677
Problem solving – lesson 7: estimate volume – page no. 678.
Lesson 8: Volume of Rectangular Prisms
Share and Show – Lesson 8: Volume of Rectangular Prisms – Page No. 683
Unlock the problem – lesson 8: volume of rectangular prisms – page no. 684.
Lesson 9: Algebra Apply Volume Formulas
Share and Show – Lesson 9: Algebra Apply Volume Formulas – Page No. 689
Problem solving – lesson 9: algebra apply volume formulas – page no. 690.
Lesson 10: Problem Solving Compare Volumes
Share and Show – Lesson 10: Problem Solving Compare Volumes – Page No. 695
On your own – lesson 10: problem solving compare volumes – page no. 696.
Lesson 11: Find Volume of Composed Figures
Share and Show – Lesson 11: Find Volume of Composed Figures – Page No. 701
Problem solving – lesson 11: find volume of composed figures – page no. 702.
Chapter Review/Test
Chapter Review/Test – Page No. 705
Chapter review/test – page no. 706, chapter review/test – page no. 707, chapter review/test – page no. 708, chapter review/test – page no. 709, chapter review/test – page no. 710.
- Chapter Review/Test – Page No. 4910
Chapter Review/Test – Page No. 4920
Chapter review/test – page no. 4930, chapter review/test – page no. 4940.

Answer: Triangle
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of three sides. So, the name of the polygon is a triangle.
Question 1. b. Are all the sides and all the angles congruent? _____
Answer: Yes
Explanation: When line segments have the same length or when angles have the same measure, they are congruent. All sides are equal in the above figure. Thus the above figure is congruent.
Question 1. c. Is the polygon a regular polygon? _____
Explanation: In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above figure is a regular polygon.
Name each polygon. Then tell whether it is a regular polygon or not a regular polygon.

Answer: i. Hexagon ii. Regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of 6 sides. So, the name of the polygon is Hexagon. In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above figure is a regular polygon.

Answer: i. Quadrilateral ii. Not regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of 4 sides. So, the name of the polygon is Quadrilateral. The above figure doesn’t have the same sides thus the above figure is not a regular polygon.

Answer: i. Octagon ii. Regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of 8 sides. So, the name of the polygon is Octagon. In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above Octagon is a regular polygon.

Answer: i. Quadrilateral ii. Regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of 4 sides. So, the name of the polygon is Quadrilateral. In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above Quadrilateral is a regular polygon.

Answer: i. Triangle ii. Not regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of three sides. So, the name of the polygon is a triangle. The above figure doesn’t have the same sides thus the above figure is not a regular polygon.

Answer: i. Heptagon ii. Regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of 7 sides. So, the name of the polygon is Heptagon. In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above Heptagon is a regular polygon.

Answer: i. Hexagon ii. Not regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of six sides. So, the name of the polygon is a Hexagon. The above figure doesn’t have the same sides and angles thus the above figure is not a regular polygon.

Answer: i. Pentagon ii. Not regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of five sides. So, the name of the polygon is a pentagon. The above figure doesn’t have the same sides and angles thus the above figure is not a regular polygon.

Answer: i. Pentagon ii. Regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of five sides. So, the name of the polygon is a pentagon. In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above Pentagon is a regular polygon.

Question 11. Which polygons in the floor plan have four equal sides and four congruent angles? How many of these polygons are there? polygon: __________ The number of polygons: __________
Answer: polygon: Quadrilateral The number of polygons: 8
Explanation: By seeing the above figure we can say that there are eight Quadrilaterals in the octagon. And the number of polygons is 8.
Question 12. Is there a quadrilateral in the floor plan that is not a regular polygon? Name the quadrilateral and tell how many of the quadrilaterals are in the floor plan. Name of quadrilateral: __________ The number of quadrilaterals: __________
Answer: Name of quadrilateral: Trapezoid The number of quadrilaterals: 8
Explanation: The name of the Quadrilateral for the above figure is Trapezoid. There is 8 number of quadrilaterals in the floor plan.
Question 13. Sketch eight points. Then connect the points to draw a closed plane figure. What kind of polygon did you draw? __________
Answer: Octagon
Question 14. Look at the angles for all regular polygons. As the number of sides increases, do the measures of the angles increase or decrease? What pattern do you see? angles measures __________
Answer: Increase
Explanation: As the number of sides increases, the measures of the angles increase. we know that The measure of the interior angle in a regular polygon is equal to x = (n-2)/n(180°) where n is the number of sides of the regular polygon. x is the measure of the interior angle in a regular polygon.

Classify each triangle. Write isosceles, scalene, or equilateral.
Then write acute, obtuse, or right.

Answer: △ – Scalene ∠ – Acute
Explanation: The 3 sides of the triangle are unequal. If three sides of the triangle are different it is known as Scalene. The angles are less than 90° thus the angle is known as an acute angle.

Answer: △ – Equilateral ∠ – Acute
Explanation: The 3 sides of the triangle are equal. If three sides of the triangle are equal it is known as the equilateral triangle. The angles are less than 90° thus the angle is known as an acute angle.

△ – Isosceles ∠ – Acute
Explanation: The 2 sides of the triangle are equal and the third side is not equal. If two sides of the triangle are different it is known as Isosceles. The angles are less than 90° thus the angle is known as an acute angle.
On Your Own

Answer: △ – Scalene ∠ – Right
Explanation: The 3 sides of the triangle are unequal. If three sides of the triangle are different it is known as Scalene. One of the angle is 90° thus the angle is known as a right angle.

Answer: △ – Isosceles ∠ – Acute

Answer: △ – Scalene ∠ – Obtuse
Explanation: The 3 sides of the triangle are unequal. If three sides of the triangle are different it is known as Scalene. The angles are more than 90° thus the angle is known as an obtuse angle.
A triangle has sides with the lengths and angle measures given.
Question 7. sides: 3.5 cm, 6.2 cm, 3.5 cm angles: 27°, 126°, 27° △ __________ ∠ __________
Answer: △ – Isosceles ∠ – Obtuse
Explanation: The 2 sides of the triangle are equal and the third side is not equal. If two sides of the triangle are different it is known as Isosceles. One of the angle is more than 90° thus the angle is known as an obtuse angle.
Question 8. sides: 2 in., 5 in., 3.8 in. angles: 43°, 116°, 21° △ __________ ∠ __________
Explanation: The 3 sides of the triangle are unequal. If three sides of the triangle are different it is known as Scalene. One of the angle is more than 90° thus the angle is known as an obtuse angle.

Question 10. Draw 2 equilateral triangles that are congruent and share a side. What polygon is formed? Is it a regular polygon? What polygon is formed? __________ Is it a regular polygon? __________
Answer: The name for the polygon is Quadrilateral. In a regular polygon, all sides are congruent and all angles are congruent.
Question 11. What’s the Error? Shannon said that a triangle with exactly 2 congruent sides and an obtuse angle is an equilateral obtuse triangle. Describe her error. Type below: __________
Answer: All angles of an equilateral triangle are acute. You cannot have an obtuse angle in an equilateral angle. And all of the angles must be congruent.
Question 12. Test Prep Which kind of triangle has exactly 2 congruent sides? Options: a. isosceles b. equilateral c. scalene d. right
Answer: isosceles
Explanation: An isosceles triangle, therefore, has both two equal sides and two equal angles. Thus the correct answer is option A.

Classify the triangles in the structures below. Write isosceles, scalene, or equilateral. Then write acute, obtuse, or right.

Answer: △ – Equilateral triangle ∠ – Acute
Explanation: From the figure, we can see an equilateral triangle. In an equilateral triangle, all sides will be less than 90°. So it is an acute angle.

Answer: △ – Scalene triangle ∠ – Right
Explanation: In the above figure, we can see a right-angle triangle. The three sides of the above triangle is different. So, it is known as the scalene triangle.

Explanation: The above figure consists of same sides. Thus the above Quadrilateral is congruent.
Question 1. b. How many right angles, if any, does the quadrilateral have? _____
The above figure doesn’t have any straight line. Thus the above figure has 0 right angles.
Question 1. c. How many pairs of parallel sides, if any, does the quadrilateral have? _____ pairs
Explanation: The above has two parallel sides. Yes, the Quadrilateral has the parallel sides.
Question 1. So, quadrilateral ABCD is a ______________ . _________
Answer: Parallelogram
Explanation: A parallelogram is a special trapezoid with opposite sides are equal.
Classify the quadrilateral in as many ways as possible.
Write quadrilateral, parallelogram, rectangle, rhombus, square, or trapezoid.

Answer: The possible ways of Quadrilateral are: 1. Rectangle 2. Parallelogram 3. Quadrilateral

Answer: The possible ways of Quadrilateral are: 1. Quadrilateral 2. Trapezoid

Answer: The possible ways of Quadrilateral for the above figure are: 1. Square 2. Quadrilateral 3. Parallelogram 4. Rectangle 5. Rhombus

Answer: The possible ways of Quadrilateral for the above figure are: 1. Trapezoid 2. Parallelogram

Answer: The possible ways of Quadrilateral for the above figure are: 1. Rhombus 2. Parallelogram 3. Square

Answer: The possible ways of Quadrilateral for the above figure are: 1. Rectangle 2. Parallelogram
Solve the problems.
Question 8. A quadrilateral has exactly 2 congruent sides. Which quadrilateral types could it be? Which quadrilaterals could it not be? Type below: _________
Answer: A rectangle has 2 congruent sides.
Explanation: The type of quadrilateral that has two congruent sides is a rectangle.
Question 9. What’s the Error? A quadrilateral has exactly 3 congruent sides. Davis claims that the figure must be a rectangle. Why is his claim incorrect? Use a diagram to explain your answer. Type below: _________
Answer: Daviss’s claim is incorrect because a rectangle does not have three congruent sides.
Go Math Grade 5 Lesson 11.3 Homework Answers Question 10. The opposite corners of a quadrilateral are right angles. The quadrilateral is not a rhombus. What kind of quadrilateral is this figure? Explain how you know. Type below: _________

Question 11. I am a figure with four sides. I can be placed in the following categories: quadrilateral, parallelogram, rectangle, rhombus, and square. Draw me. Explain why I fit into each category. Type below: _________

Question 12. Test Prep A quadrilateral has exactly 1 pair of parallel sides and no congruent sides. What type of quadrilateral is it? Options: a. rectangle b. rhombus c. parallelogram d. trapezoid
Answer: Trapezoid
Explanation: A quadrilateral with one pair of parallel sides is a trapezoid. Thus the correct answer is option D.

Question 1. Then, fold the triangle to match each pair of sides to determine if at least two of the sides are congruent. As you test the sides, record or draw the results for each pair to make sure that you have checked all pairs of sides. Possible drawings are shown. Type below: _________
Question 1. Finally, answer the question. ______
Question 2. What if Erica also wants to show, without using a protractor, that the triangle has one right angle and two acute angles? Explain how she can show this.
Answer: The sum of three angles = 180 If one of the angles is 90 then the other two angles will be acute angles.
Question 3. December, January, and February were the coldest months in Kristen’s town last year. February was the warmest of these months. December was not the coldest. What is the order of these months from coldest to warmest? Coldest: _________ _________ Warmest: _________ _________
Answer: Coldest: January December Warmest: February
Explanation: January and December are the coldest months of the year depending on the direction of the wind. February is the warmest month among these months.
Question 4. Jan enters a 20-foot by 30-foot rectangular room. The long sides face north and south. Jan enters the exact center of the south side and walks 10 feet north. Then she walks 8 feet east. How far is she from the east side of the room? ______ ft
Answer: 7 feet
Explanation: Given that, Jan enters a 20-foot by 30-foot rectangular room. The long sides face north and south. Jan enters the exact center of the south side and walks 10 feet north. Then she walks 8 feet east. Jan is 7 feet from the east wall in the room.

Answer: 3 lines
Explanation: From the above figure, we can see that there are 18 congruent squares. To find the least number of lines Max can draw we have to divide the number of squares by the number of congruent rectangles 18 ÷ 6 = 3 Thus the least number of lines that Max can Draw is 3 lines.
Geometry Chapter 11 Test Answer Key Go Math Grade 5 Workbook Question 6. Of the 95 fifth and sixth graders going on a field trip, there are 27 more fifth graders than sixth graders. How many fifth graders are going on the field trip? 5th graders = ______
Explanation: Since we are not told how many 6th graders are going on the trip let’s use a variable, the letter x. Now let’s understand the problem in the “math” language. x= the number of 6th graders. X+27= the number of 5th graders since there are 27 more fifth-graders than sixth graders. x+x+27 = 95 2x+27=95 -27 -27 2x+ 0 =68 2x=68 divide by 2 on both sides. x = 34 Now, remember how x+27 = the number of 5th graders going on the trip? Since we know that x=34, substitute the x as 34+27 which = 61 fifth graders going on the trip.

Question 7. Sam’s paper route begins and ends at the corner of Redwood Avenue and Oak Street. His route is made up of 4 streets, and he makes no 90° turns. What kind of polygon do the streets of Sam’s paper route form? Name the streets in Sam’s route. _________
Explanation: Given that, Sam’s paper route begins and ends at the corner of Redwood Avenue and Oak Street. His route is made up of 4 streets, and he makes no 90° turns. By following the route map we can say that the polygon is a parallelogram.
Question 8. Sam’s paper route includes all 32 houses on two pairs of parallel streets. If each street has the same number of houses, how many houses are on each street? Name the parallel streets. ______ houses on each street
Explanation: Given, Sam’s paper route includes all 32 houses on two pairs of parallel streets. If each street has same number of houses we have to divide 32 by 4 32 ÷ 4 = 8 Thus there are 8 houses on each street.

Explanation: A square is a type of quadrilateral that has opposite sides that are congruent and parallel. Thus the correct answer is option B.
Classify the solid figure. Write prism, pyramid, cone, cylinder, or sphere.

Answer: Triangular prism
Explanation: A triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise, it is oblique.

Answer: Sphere
Explanation: A sphere has no bases and 1 curved surface.
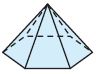
Answer: Hexagonal Base Pyramid
Explanation: A pyramid that has a hexagonal base, that is, a base with six sides and 6 triangular lateral faces, then it is a hexagonal pyramid.

Answer: Pentagonal prism
Explanation: A pentagonal prism is a prism that has two pentagonal bases top and bottom and five rectangular sides. It is a type of heptahedron with 7 faces, 10 vertices, and 15 edges.

Answer: Pentagonal Base Pyramid
Explanation: In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point.

Answer: Cylinder
Explanation: A cylinder has 2 congruent circular bases and 1 curved surface.

Answer: Rectangular prism
Explanation: A rectangular prism is a polyhedron with two congruent and parallel bases. It is also a cuboid. It has six faces, and all the faces are in a rectangle shape and have twelve edges. Because of its cross-section along the length, it is said to be a prism.

Answer: Cone
Explanation: A cone has 1 circular base and 1 curved surface.

Answer: Triangle base pyramid
Explanation: A triangle-based pyramid has four triangular sides. The base can be any shape or size of the triangle but usually, it is an equilateral triangle. This means the three sides of the pyramid are the same size as each other and the pyramid looks the same if you rotate it.

Explanation: A prism’s base shape is used to name the solid figure. The base shape of this prism is a triangle. The prism is a triangular prism.

Answer: Hexagonal Prism
Explanation: In geometry, the hexagonal prism is a prism with a hexagonal base. This polyhedron has 8 faces, 18 edges, and 12 vertices. Since it has 8 faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces.

Answer: Square Pyramid
Explanation: In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid and has symmetry. If all edges are equal, it is an equilateral square pyramid.

Answer: Octogonal Prism
Explanation: In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps. If the faces are all regular, it is a semiregular polyhedron.
Question 16. Mario is making a sculpture out of stone. He starts by carving a base with five sides. He then carves five triangular lateral faces that all meet at a point at the top. What three-dimensional figure does Mario make? _________
Answer: Pentagonal Pyramid
Explanation: Given, Mario is making a sculpture out of stone. He starts by carving a base with five sides. He then carves five triangular lateral faces that all meet at a point at the top. The polygon which has 5 sides is a pentagon. The three-dimensional figure which meets at the same point is the pyramid. The 3-dimensional figure that Mario makes is Pentagonal Pyramid So, the answer to the above question is Pentagonal Pyramid.
Question 17. What is another name for a cube? Explain your reasoning. Type below: _________
Answer: The cube can also be called a regular hexahedron. It is one of the five regular polyhedrons, which are also sometimes referred to as the Platonic solids.
Connect to Reading
Example Read the description. Underline the details you need to identify the solid figure that will name the correct building.

Identify the solid figure and name the correct building.
Question 18. Solve the problem in the Example. Solid figure: _________ Building: _________
Answer: i. Pyramid ii. Luxor Hotel-Las Vegas-Nevada
Explanation: The 3rd figure is in the form of a pyramid. The name of the pyramid-shaped building is Luxor Hotel Las Vegas-Nevada.
Go Math Grade 5 Chapter 11 Answer Key Pdf Question 19. This building was completed in 1902. It has a triangular foundation and a triangular roof that are the same size and shape. The three sides of the building are rectangles. Solid figure: _________ Building: _________
Answer: i. prism ii. Flatiron Building-New York City-New York
Explanation: The triangle-shaped figure is in the form of a prism. The name of the triangular prism building is Flatiron Building-New York, New York.

Question 1. A closed plane figure with all sides congruent and all angles congruent is called a ________ . _________
Answer: Regular Polygon
Question 2. Line segments that have the same length or angles that have the same measure are __________ . _________
Answer: Congruent
Concepts and Skills

Answer: i. Hexagon ii. Regular Polygon

Answer: i. Triangle ii. Non-Regular

Answer: i. Pentagon ii. Not Regular

Answer: i. Equilateral ii. Acute

Answer: i. Isosceles ii. Right
Answer: i. Isosceles ii. Obtuse
Classify the quadrilateral in as many ways as possible. Write quadrilateral, parallelogram, rectangle, rhombus, square, or trapezoid.

Answer: 1. Quadrilateral 2. Trapezoid
Answer: 1. Quadrilateral 2. Parallelogram 3. Rectangle

Answer: 1. Quadrilateral 2. Parallelogram 3. Rhombus 4. Rectangle 5. Square
Fill in the bubble completely to show your answer.

Answer: right isosceles
Explanation: The above figure is a right angle and the two sides of the triangle are equal. The above figure is a right isosceles. Thus the correct answer is option A.

Answer: quadrilateral, parallelogram, rhombus, rectangle, square

Explanation: The 3-dimensional figure of the above rectangle is a rectangular prism. Thus the correct answer is option C.
Count the number of cubes used to build each solid figure.
Explanation: By seeing the above figure we can say that the rectangular prism has 3 unit cubes.

Explanation: The above figure shows that there are 5 congruent squares of 3 lines. 5 × 3 = 15 unit cubes

Explanation: The above figure shows that there are 4 congruent squares of 3 lines. 4 × 3 = 12 unit cubes

Explanation: The above figure shows that there are 6 congruent squares of 2 lines. 6 × 2 = 12

Explanation: By seeing the above figure we can say that there are 5 unit cubes.

Explanation: There are 6 congruent squares in the above figure.

Explanation: The figure shows that there are 7 unit cubes.
Question 8. How are the rectangular prisms in Exercises 3–4 related? Can you show a different rectangular prism with the same relationship? Explain. Type below: _________

Compare the number of unit cubes in each solid figure. Use < , > or =.

Use the information to answer the questions.

Question 11. There are 38 Cube Houses. Each house could hold 1,000 unit cubes that are 1 meter by 1 meter by 1 meter. Describe the dimensions of a cube house using unit cubes. Remember that the edges of a cube are all the same length. Each dimension = ______ meters
Answer: 10 meters
Explanation: So each house can hold 1000 cubes that are 1 meter in length. The house is also shaped like a cube, so you need to cube-root 1000. The cube root of 1000 is 10. So the cube house has a length, width, and height of 10 meters. V = lbh V = 10 m × 10 m × 10 m = 1000 cu. meter Thus Each dimension is 10 meters.
Understanding Volume 5th Grade Geometry Answers Question 12. The Nakagin Capsule Tower has 140 modules and is 14 stories high. If all of the modules were divided evenly among the number of stories, how many modules would be on each floor? How many different rectangular prisms could be made from that number? Type below: _________
Answer: 10 modules on each floor
Explanation: The Nakagin Capsule Tower has 140 modules and is 14 stories high. Divide 140 modules by 14 140 ÷ 14 = 10 Thus 10 modules would be on each floor. The factors of 10 are 1, 2, 5. 1 × 10 = 10 2 × 5 = 10 Thus 2 different rectangular prisms can be made from 10 unit cubes.
Use the unit given. Find the volume.

Answer: 48 cu. cm
Explanation: Given that, L = 4cm B = 4cm H = 3 cm We know that, The volume of the cuboid is lbh V = 4 cm × 4 cm × 3 cm = 48 cubic cm Thus the volume for the above cube is 48 cubic cm.

Answer: 24 cu. in.
Explanation: Given that, L = 3 in B = 2 in H = 4 in. We know that, The volume of the cuboid is lb V = 3 in × 2 in × 4 in = 24 cubic inches Therefore the volume for the above cube is 24 cubic inches.

Answer: 36 cu. ft
Explanation: Given that, L = 6 ft B = 2 ft H = 3 ft We know that, The volume of the cuboid is lbh V = 6 ft × 2 ft × 3 ft = 36 cubic feet V = 36 cu. ft Therefore the volume for the above figure is 36 cu. ft

Answer: 60 cu. in
Given that, L = 5 in. B = 4 in. H = 3 in. We know that, The volume of the cuboid is lbh V = 5 in × 4 in × 3 in = 60 cubic inches Thus the volume for the above figure is 60 cu. in.
Compare the volumes. Write < , >, or =.

Question 7. What’s the Error? Jerry says that a cube with edges that measure 10 centimeters has a volume that is twice as much as a cube with sides that measure 5 centimeters. Explain and correct Jerry’s error. Type below: __________
Answer: Let v1 equal the 10 cm sided cube’s volume. Let v2 equal the 5 cm sided cube’s volume. v1 = 10 × 10 10 = 1000 cu. cm v2 = 5 × 5 × 5 = 125 cu. cm To find the relationship between the two volumes, divide the first volume by the second. r = v1 ÷ v2 r = 1000 ÷ 125 = 8 The volume differ by a factor of 8. Thus the volume differs by a factor of 8, not by a factor of 2.
Question 8. Pattie built a rectangular prism with cubes. The base of her prism has 12 centimeter cubes. If the prism was built with 108 centimeter cubes, how many layers does her prism have? What is the height of her prism? layers: ______ the height of the prism: ______ cm
Answer: 9 layers, the height of the prism is 9 cm
Explanation: Given: Pattie built a rectangular prism with cubes. The base of her prism has 12-centimeter cubes. The prism was built with 108 cm cubes. To find the layers divide the number of cubes by base of the prism That means 108 ÷ 12 108/12 = 9 Thus the prism has 9 layers. Now we have to find the base of the prism 108 = b × h 12 × h = 108 h = 108/12 = 9 Therefore the height of the prism = 9 cm
Question 9. A packing company makes boxes with edges each measuring 3 feet. What is the volume of the boxes? If 10 boxes are put in a larger, rectangular shipping container and completely fill it with no gaps or overlaps, what is the volume of the shipping container? volume of the boxes: __________ cu ft volume of the shipping container = __________ cu ft
Answer: the volume of the boxes: 27 cu ft the volume of the shipping container = 27 cu ft
Explanation: A packing company makes boxes with edges each measuring 3 feet. Volume of the cube = lbh V = 3 × 3 × 3 = 27 cubic feet Thus the volume of the boxes is 27 feet. The volume of the boxes for 10 boxes is 27 × 10 = 270 cubic feet Therefore the volume of the shipping container is 27 cu ft

Answer: 75 cubic centimeters
Explanation: L = 5 cm B = 3 cm H = 5 cm Volume of the rectangular prism is lbh V = 5 cm × 3 cm × 5 cm = 75 cubic centimeter V = 75 cu. cm Thus the correct answer is option D.
Estimate the volume.

Answer: Given that the volume of each box is 125 cubic inches. By seeing the above figure we can say that there are 9 boxes in the larger box. Thus there are 9 tissue boxes in the larger box. Now to find the volume of the tissue boxes. We have to multiply the number of boxes with the volume of the box V = 125 × 9 = 1125 cubic inches. Therefore The estimated volume of the box holding the tissue boxes is 1125 cubic inches.

Answer: Given that, the volume of the chalk box is 16 cubic inches. From the figure, we can see that there are 24 boxes. The volume of the large box is 24 × 16 = 384 cubic inches. Therefore the estimated volume of the large box is 384 cu in.

Answer: Given, the volume of the small jewelry box is 30 cu cm There are 10 small jewelry boxes. V = 30 × 10 = 300 cu. cm Thus the estimated volume of large box is 300 cu. cm

Answer: Given that, the volume of the book is 80 cu. in There are 12 books in the figure. Multiply the number of books with the volume of each book = 12 × 80 = 960 cu. inches Thus the estimated volume of large books is 960 cu in.

Answer: Volume of spaghetti box is 750 cu. cm Volume = 2 × 5 × 4 = 40 Number of boxes = 40 Now multiply 40 with 750 cu. cm to find the volume of large box V = 40 × 750 cu. cm V = 30000 cubic cm Therefore the estimated Volume of large box is 30000 cubic cm

Answer: Given the volume of a cereal box is 324 cu. in Number of boxes is 2 × 3 × 3 = 18 The volume of large box is 18 × 324 cu. in V = 18 × 324 cu. in = 5832 cubic inches Thus the estimated Volume of large box is 5832 cubic inches.

Answer: Volume of pencil box is 4500 cu cm Number of pencil boxes = 2 × 5 = 10 The volume of large box is 4500 × 10 = 45000 cu cm Thus the estimated volume of large box is 45000 cu cm
Sense or Nonsense?

Answer: Calculate the books in box 1 V = lbh V1 = 2 × 4 × 7 = 56 books Calculate the volume of books in box 2 V = lbh V2 = 1 × 4 × 14 = 56 books So, both boxes hold the same number of books. Thus Marcelle’s statement make sense.
Find the volume.

Answer: 120 cu. in
Explanation: From the figure, we can say that the length of the rectangular prism is 4 in The width of the rectangular prism is 5 in The height of the rectangular prism is 6 in. The volume of the rectangular prism is l × w × h V = 4 in × 6 in × 5 in = 120 cu. in So, the volume of the prism is 120 cu. in

Explanation: From the figure, we can say that the length of the rectangular prism is 2 cm The width of the rectangular prism is 3 cm The height of the rectangular prism is 3 cm The volume of the rectangular prism is l × w × h V = 2 cm × 3 cm × 3 cm = 18 cu. cm Thus the volume of the rectangular prism is 18 cu. cm

Explanation: From the figure, we can say that the length of the rectangular prism is 2 in. The width of the rectangular prism is 6 in. The height of the rectangular prism is 1 in. The volume of the rectangular prism is l × w × h V = 2 in × 6 in × 1 in V = 12 Cu in. Thus the volume of the rectangular prism is 12 Cu in.

Explanation: From the figure, we can say that the length of the rectangular prism is 1 mm The width of the rectangular prism is 8 mm The height of the rectangular prism is 3 mm The volume of the rectangular prism is l × w × h V = 1 mm × 8 mm × 3 mm V = 24 Cu. mm Thus the volume of the rectangular prism is 24 Cu. mm

Answer: 160
Explanation: From the figure, we can say that the length of the rectangular prism is 10 cm The width of the rectangular prism is 4 cm The height of the rectangular prism is 4 cm The volume of the rectangular prism is l × w × h V = 10 cm × 4 cm × 4 cm = 160 Cu. cm Thus the volume of the rectangular prism is 160 Cu. cm

Answer: 150
Explanation: From the figure, we can say that the length of the rectangular prism is 5 ft The width of the rectangular prism is 6 ft The height of the rectangular prism is 5 ft The volume of the rectangular prism is l × w × h V = 5 ft × 6 ft × 5 ft V = 150 Cu. ft Thus the volume of the rectangular prism is 150 Cu. ft

Answer: 196
Explanation: From the figure, we can say that the length of the rectangular prism is 7 in. The width of the rectangular prism is 7 in. The height of the rectangular prism is 4 in. The volume of the rectangular prism is l × w × h V = 7 in × 7 in × 4 in = 196 Cu. in Thus the volume of the rectangular prism is 196 Cu. in

Answer: We need to find the volume of the travel crate that Rich should build.
Question 8. b. How can you use Thomas’s size to help you solve the problem? Type below: _________
Answer: Thomas’s size helps to find the length, width and height of the dog crate.
Question 8. c. What steps can you use to find the size of Thomas’s crate? Type below: _________
Answer: Rich is building a travel crate for his dog, Thomas, a beagle mix who is about 30 inches long, 12 inches wide, and 24 inches tall. For Thomas to travel safely, his crate needs to be a rectangular prism that is about 12 inches greater than his length and width, and 6 inches greater than his height. Length of the dog crate is 30 in + 12 in = 42 inches Width of the dog crate is 12 inches more than width of Thomas crate = 12 in + 12 in = 24 inches Height of the dog crate is 24 in + 6 in = 30 inches V = 42 in × 24 in × 30 in V = 30,240 cu in
Question 8. d. Fill in the blanks for the dimensions of the dog crate. length: _____ width: _____ height: _____ area of base: _____ Type below: _________
Answer: Crate length = 30 + 12 = 42 in Crate width = 12 + 12 = 24 in Crate height = 24 + 6 = 30 in Area of base = l × w A = 42 in × 24 in = 1008 sq in.
Question 8. e. Find the volume of the crate by multiplying the base area and the height. ______ × ______ = ______ So, Rich should build a travel crate for Thomas that has a volume of ______ . Type below: _________
Answer: Area of base = l × w A = 42 in × 24 in = 1008 sq in. Height = 30 in V = 1008 sq in × 30 in = 30240 cu. in So, Rich should build a travel crate for Thomas that has a volume of 30240 cu. in

Answer: 175 in. 3
Explanation: Length = 5 in Width = 7 in Height = 5 in Volume of the rectangular prism is l × w × h V = 5 in × 7 in × 5 in V = 175 in. 3 The volume of the rectangular prism is 175 in. 3 Therefore the correct answer is option D.

Explanation: length = 2 ft width = 4 ft height = 5 ft Volume of the rectangular prism is l × w × h V = 2 ft × 4 ft × 5 ft V = 40 cu ft Volume of the rectangular prism is 40 cu. ft

Answer: 144
Explanation: length = 4 cm width = 4 cm height = 9 cm Volume of the rectangular prism is l × w × h V = 4 cm × 4 cm × 9 cm V = 144 cu cm Volume of the rectangular prism is 144 cu cm

Answer: 216
Explanation: length = 6 in width = 6 in height = 6 in Volume of the prism is l × w × h V = 6 in × 6 in × 6 in V = 216 cu. in Thus the Volume of the prism is 216 cu. in.

Answer: 192
Explanation: length = 12 ft width = 4 ft height = 4 ft Volume of the rectangular prism is l × w × h V = 12 ft × 4 ft × 4 ft V = 192 cu ft Therefore, the Volume of the rectangular prism is 192 cu ft.

Answer: 240
Explanation: length = 10 cm width = 6 cm height = 4 cm Volume of the rectangular prism is l × w × h V = 10 cm × 6 cm × 4 cm V = 240 Cu. cm Therefore, the Volume of the rectangular prism is 240 Cu. cm.

Answer: 1008
Explanation: length = 14 in. width = 6 in. height = 12 in. Volume of the rectangular prism is l × w × h V = 14 in × 6 in × 12 in V = 1008 cu. in Thus the Volume of the rectangular prism is 1008 cu. in

Explanation: length = 7 ft width = 6 ft height = ■ ft Volume of the rectangular prism is l × w × h 420 cu ft = 7 ft × 6 ft × ■ ■ × 42 sq ft = 420 cu ft ■ = 420 cu ft ÷ 42 sq ft ■ = 10 ft

Explanation: length = 6 cm width = 15 cm height = ■ cm Volume of the rectangular prism is l × w × h V = 900 cu cm 900 cu cm = 6 cm × 15 cm × ■ cm 900 cu cm = 90 sq cm × ■ cm ■ cm = 900 cu cm ÷ 90 sq cm ■ cm = 10 cm

Answer: 40 cu ft of water
Explanation: The Jade Restaurant has a large aquarium on display in its lobby. The base of the aquarium is 5 feet by 2 feet. The height of the aquarium is 4 feet. Volume = b × w × h V = 5 feet × 2 feet× 4 feet V = 40 Cu. ft Therefore, the volume of the aquarium is 40 cu ft of water.
Question 10. The Pearl Restaurant put a larger aquarium in its lobby. The base of their aquarium is 6 feet by 3 feet, and the height is 4 feet. How many more cubic feet of water does the Pearl Restaurant’s aquarium hold than the Jade Restaurant’s aquarium? ____ cu ft
Answer: 32 cu ft
Explanation: The Pearl Restaurant put a larger aquarium in its lobby. The base of their aquarium is 6 feet by 3 feet, and the height is 4 feet. Volume = b × w × h V = 6 feet × 3 feet × 4 feet = 72 cu. feet Thus the Volume of Pearl Restaurant’s aquarium is 72 cu. feet The volume of the Jade Restaurant’s aquarium is 40 cu ft of water V = Vp – Vj V = 72 – 40 = 32 cu feet
Question 11. Eddie measured his aquarium using a small fish food box. The box has a base area of 6 inches and a height of 4 inches. Eddie found that the volume of his aquarium is 3,456 cubic inches. How many boxes of fish food could fit in the aquarium? Explain your answer. ____ boxes
Answer: 144 boxes
Explanation: Volume = b × h V = 6 in × 4 in = 24 cu in To find out how many boxes will fit, divide the aquarium volume by the food box volume. numfit = Vaq/Vbox numfit = 3456/24 = 144 144 fish food boxes fir inside the aquarium.
Question 12. Describe the difference between area and volume. Type below: _________
Answer: The surface area is the sum of the areas of all the faces of the solid figure. It is measured in square units. Volume is the number of cubic units that make up a solid figure.

Answer: 1,050 cubic centimeters
Explanation: L = 15 cm W = 10 cm H = 7 cm V = lwh V = 15 cm × 10 cm × 7 cm = 1050 cubic centimeters Thus the correct answer is option C.
Question 1. Mr. Price makes cakes for special occasions. His most popular-sized cakes have a volume of 360 cubic inches. The cakes have a height, or thickness, of 3 inches, and have different whole number lengths and widths. No cakes have a length or width of 1 or 2 inches. How many different cakes, each with a different-size base, have a volume of 360 cubic inches? First, think about what the problem is asking you to solve, and the information that you are given. Next, make a table using the information from problem. Finally, use the table to solve the problem. Type below: _________
Answer: There are total of 8 different possible combination of length and width
Explanation: Volume = 360 cubic inches Height = 3 inches Volume = l x w x h 360 = l x w x 3 l x w = 120 The factors of 120 are, 1 x 120, 2x 60, 3 x 40, 4 x 30, 5 x 24, 6 x 20, 8 x 15, 10 x 12
Question 2. What if the 360 cubic-inch cakes are 4 inches thick and any whole number length and width are possible? How many different cakes could be made? Suppose that the cost of a cake that size is $25, plus $1.99 for every 4 cubic inches of cake. How much would the cake cost? Type below: _________
Answer: Since the store have a volume of 360 cu in and a height of 4 in. We need to find the number of different stones which have a base of 90 sq in. V = b × h B = 360 cu in/4 in B = 90 sq in. Consider the factors of 90. The factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90 Make a table with the base, height and volume for each pair of factors Height = 4 in 1 × 90 × 4 = 360 cu in 2 × 45 × 4 = 360 cu in 3 × 30 × 4 = 360 cu in 5 × 18 × 4 = 360 cu in 6 × 15 × 4 = 360 cu in 9 × 10 × 4 = 360 cu in 6 different sized paving stones. Remember that each store has a volume of 360 cu in. Divide by 4 to find how many 4 cu in per stone Concrete = $0.18 × (360/4) = $0.18 × 90 = $18.70 The cost of the stone plus the concrete cost = $2.50 + concrete Cost = $2.50 + $16.20 = $18.70
Question 3. One company makes inflatable swimming pools that come in four sizes of rectangular prisms. The length of each pool is twice the width and twice the depth. The depth of the pools are each a whole number from 2 to 5 feet. If the pools are filled all the way to the top, what is the volume of each pool? Type below: _________
Answer: If the depth of the pool is 2 feet then the length of the pool is twice the width and twice the depth That means 2 feet × 2 × 2 = 8 feet Width is twice the depth W = 2 feet × 2 = 4 feet The volume of the rectangular swimming pool is l × w × h V = 8 ft × 4 feet × 2 ft V = 64 cu ft If the depth of the pool is 3 feet then the length of the pool is twice the width and twice the depth That means 3 feet × 2 × 2 = 12 feet Width is twice the depth W = 3 feet × 2 = 6 feet The volume of the rectangular swimming pool is l × w × h V = 12 ft × 6 feet × 2 ft V = 144 cu ft If the depth of the pool is 4 feet then the length of the pool is twice the width and twice the depth That means 4 feet × 2 × 2 = 16 feet Width is twice the depth W = 4 feet × 2 = 8 feet The volume of the rectangular swimming pool is l × w × h V = 16 ft × 8 feet × 2 ft V = 256 cu ft If the depth of the pool is 5 feet then the length of the pool is twice the width and twice the depth That means 5 feet × 2 × 2 = 20 feet Width is twice the depth W = 5 feet × 2 = 10 feet The volume of the rectangular swimming pool is l × w × h V = 20 ft × 10 feet × 2 ft V = 400 cu ft
Question 4. Ray wants to buy the larger of two aquariums. One aquarium has a base that is 20 inches by 20 inches and a height that is 18 inches. The other aquarium has a base that is 40 inches by 12 inches and a height that is 12 inches. Which aquarium has a greater volume? By how much? Type below: _________
Answer: 1440 cu. in
Explanation: Volume = l × w × h Volume of Aquarium 1 = 20 in × 20 in × 18 in V = 7200 cu. in Volume = l × w × h Volume of Aquarium 2 is 40 in × 12 in × 12 in V for A2 = 5760 cu in A1 > A2 A1 has a greater volume. Subtract A2 from A1 A1 – A2 = 7200 cu in – 5760 cu in = 1440 cu in The volume of Aquarium 1 is 1440 cu in more than Volume of Aquarium 2.
Question 5. Ken owns 13 CDs. His brother Keith has 7 more CDs than he does. Their brother, George, has more CDs than either of the younger brothers. Together, the three brothers have 58 CDs. How many CDs does George have? ______ CDs
Answer: 25 CDs
Explanation: Given that, Ken owns 13 CDs. His brother Keith has 7 more CDs than he does. Their brother, George, has more CDs than either of the younger brothers. Together, the three brothers have 58 CDs. Keith has 7 more CDs than Ken That means he has 7 + 13 = 20 CDs Now subtract Ken’s CDs, Keith CDs from the total number of CDs. = 58 – 20 – 13 = 25 CDs. Thus George has 25 CDs.
Question 6. Kathy has ribbons that have lengths of 7 inches, 10 inches, and 12 inches. Explain how she can use these ribbons to measure a length of 15 inches. Type below: _________
Answer: She could take the 10-inch ribbon and then use 5 inches from the 7-inch ribbon
Question 7. A park has a rectangular playground area that has a length of 66 feet and a width of 42 feet. The park department has 75 yards of fencing material. Is there enough fencing material to enclose the playground area? Explain. ______
Explanation: A park has a rectangular playground area that has a length of 66 feet and a width of 42 feet. The park department has 75 yards of fencing material. Area of the rectangular playground = l × w A = 66 feet × 42 feet A = 2772 sq. ft Perimeter of the rectangular playground = 2l + 2w P = 2 × 66 + 2 × 42 P = 216 ft Now convert from feet to yard We know that 1 yard = 3 feet 216 ft = 1/3 × 216 = 72 yard 72 yard is less than 75 yard Thus the park department has enough fencing material.
Question 8. Test Prep John is making a chest that will have a volume of 1,200 cubic inches. The length is 20 inches and the width is 12 inches. How many inches tall will his chest be? Options: a. 4 in. b. 5 in. c. 6 in. d. 7 in.
Answer: 5 in
Explanation: John is making a chest that will have a volume of 1,200 cubic inches. The length is 20 inches and the width is 12 inches. Volume = l × w × h 1200 cu in = 20 in × 12 in × h 240 sq in × h = 1200 cu in h = 1200 cu in ÷ 240 sq in h = 5 in Thus John’s chest will be 5 inches tall. The correct answer is option B.
Find the volume of the composite figure.

Answer: 88 cu in.
Explanation: Split the figure into 2 parts Volume of figure 1: b = 2 in h = 3 in w = 4 in V = 2 in × 4 in × 3 in V = 24 cu. in Volume of figure 2: b = 8 in w = 4 in h = 2 in V = 8 in × 4 in × 2 in V = 64 in Volume of the composite figure = 24 cu in + 64 cu. in = 88 cu. in

Answer: 48 cu cm
Explanation: Split the figure into 2 parts Volume of figure 1: b = 3 cm h = 1 cm w = 2 cm V = 3 cm × 2 cm × 1 cm V = 6 cu. cm Volume of figure 2: b = 7 cm w = 6 cm h = 1 cm V = 7 cm × 6 cm × 1 cm V = 42 cu. cm Volume of the composite figure = 42 cu. cm + 6 cu. cm = 48 cu cm

Answer: 52 cu ft
Explanation: Split the figure into 2 parts Volume of figure 1: b = 6 ft h = 2 ft w = 3 ft V = 6 ft × 3 ft × 2 ft V = 36 cu. ft Volume of figure 2: b = 4 ft w = 2 ft h = 2 ft V = 4 ft × 2 ft × 2 ft V = 16 cu. ft Volume of the composite figure = 36 cu. ft + 16 cu. ft = 52 cu ft

Answer: 108 cu. cm
Explanation: Split the figure into 2 parts Volume of figure 1: b = 3 cm w = 8 cm h = 2 cm V = 3 cm × 8 cm × 2 cm V = 48 cu cm Volume of figure 2: b = 10 cm w = 3 cm h = 2 cm V = 10 cm × 3 cm × 2 cm V = 60 cu cm Volume of the composite figure = 48 cu cm + 60 cu cm = 108 cu. cm

Answer: 204 cu. in
Explanation: Split the figure into 2 parts Volume of figure 1: b = 3 in h = 5 in w = 4 in V = 3 in × 4 in × 5 in V = 60 cu. in Volume of figure 2: b = 12 in w = 4 in h = 3 in V = 12 in × 4 in × 3 in V = 144 cu. in Volume of the composite figure = 60 cu in + 144 cu. in = 204 cu. in
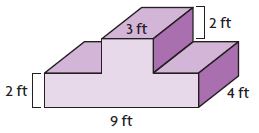
Answer: 96 cu ft
Explanation: Split the figure into 3 parts. Figure 1: V1 = 9 ft × 4 ft × 2 ft V1 = 72 cu. ft Figure 2: V2 = 3 ft × 4 ft × 2 ft V2 = 24 cu. ft V = V1 + V2 V = 72 cu. ft + 24 cu. ft = 96 cu. ft Thus the volume of the composite figure is 96 cu. ft

Answer: 300 cu. ft

Answer: 102 cu cm

Question 9. As part of a wood-working project, Jordan made the figure at the right out of wooden building blocks. How much space does the figure he made take up? ______ cu in.
Answer: 784 cu. in
Explanation: Split the figure into 2 parts Figure 1: V1 = 14 in × 4 in × 5 in V1 = 280 cu. in Figure 2: V2 = 12 in × 14 in × 3 in V2 = 504 cu. in V = V1 + V2 V = 280 cu. in + 504 cu. in V = 784 cu. in
Question 10. What are the dimensions of the two rectangular prisms you used to find the volume of the figure? What other rectangular prisms could you have used? Type below: ________
Answer: Dimensions for figure 1: Base = 14 in Width = 4 in Height = 5 in Dimensions for figure 2: Base = 12 in Width = 14 in Height = 3 in
Question 11. If the volume is found using subtraction, what is the volume of the empty space that is subtracted? Explain. ______ cu in.
Answer: 560 cu. in
Explanation: B = 8 in H = 5 in W = 14 in V = 8 in × 14 in × 5 in V = 560 cu. in Thus the volume of the empty space is 560 cu. in
Question 12. Explain how you can find the volume of composite figures that are made by combining rectangular prisms. Type below: ________

Answer: 476 cubic centimeters
Explanation: Split the figure into 2 parts Figure 1: V1 = 10 cm × 7 cm × 5 cm V1 = 350 cu. cm Figure 2: V2 = 3 cm × 7 cm × 6 cm V2 = 126 cu. cm V = V1 + V2 V = 350 cu. cm + 126 cu. cm V = 476 cu. cm
Question 1. Fran drew a triangle with no congruent sides and 1 right angle. Which term accurately describes the triangle? Mark all that apply. Options: a. isosceles b. scalene c. acute d. right
Answer: Right
Explanation: A right triangle is a type of triangle that has one angle that measures 90°. Right triangles, and the relationships between their sides and angles, are the basis of trigonometry. Thus the correct answer is option D.

Answer: Volume of the box is l × w × h V = 8 in × 10 in × 3 in V = 240 cu. in Thus the volume of the box is 240 cu. in

Answer: The figure has 3 sides and 3 angles.
Explanation: From the above figure we can say that there are three sides and three angles.

Answer: a regular polygon If all the sides are congruent then the polygon is a regular polygon.

Answer: 36 cubic feet
Explanation: Figure 1: length = 2 ft width = 3 ft height = 1 ft Volume of 1st figure = l × w × h V = 2 ft × 3 ft × 1 ft = 6 cu. ft Figure 2: length = 4 ft width = 3 ft height = 1 ft Volume of 1st figure = l × w × h V = 4 ft × 3 ft × 1 ft = 12 cu. ft Figure 3: length = 6 ft width = 3 ft height = 1 ft Volume of 1st figure = l × w × h V = 6 ft × 3 ft × 1 ft = 18 cu. ft Add all the volumes = 6 cu. ft + 12 cu. ft + 18 cu. ft Volume = 36 cu. ft

Explanation: Count the number of unit cubes in the first figure. There are 10 unit cubes in figure 1 so match the figure 1 to 10 unit cubes. Count the number of unit cubes in the second figure. There are 12 unit cubes in figure 2 so match figure 2 to 12 unit cubes. Count the number of unit cubes in the third figure. There are 9 unit cubes in figure 3 so match figure 3 to 9 unit cubes.
Question 6. Chuck is making a poster about polyhedrons for his math class. He will draw figures and organize them in different sections of the poster. Part A Chuck wants to draw three-dimensional figures whose lateral faces are rectangles. He says he can draw prisms and pyramids. Do you agree? Explain your answer. i. yes ii. no
Explanation: The lateral faces of a pyramid are triangles. The lateral faces of a prism are rectangles.
Question 6. Part B Chuck says that he can draw a cylinder on his polyhedron poster because it has a pair of bases that are congruent. Is Chuck correct? Explain your reasoning. i. yes ii. no
Explanation: A cylinder does have 2 congruent bases, but a cylinder is not a polyhedron. A cylinder has 1 curved surface, while a polyhedron has faces that are polygons

Answer: 8, 8 The above figure has 8 sides and 8 angles.

Answer: The polygon with 8 sides is known as the octagon. The above figure is congruent thus it is a regular octagon.

Explanation: Given, l = 6 in w = 3 in h = 4 in The volume of the rectangular prism is l × w × h V = 6 in × 3 in × 4in V = 72 cu in. Hence, the volume of the rectangular prism Victoria built is 72 cu. in.

Explanation: The above different have different sizes thus the triangle is scalene. The angle for the above triangle is more than 90° thus the angle is an obtuse angle. So, the answer is yes.

Explanation: The above different have different sizes thus the triangle is scalene. It has one right angle thus the statement is not correct.

Question 10. A shipping crate holds 20 shoeboxes. The dimensions of a shoebox are 6 inches by 4 inches by 12 inches. For 10a–10b, select True or False for each statement. a. Each shoebox has a volume of 22 cubic inches. i. True ii. False
Answer: False
Explanation: Shoebox volume: V = 6 in × 4 in × 12 in V = 288 cu. in Thus the statement is false.
Question 10. b. Each crate has a volume of about 440 cubic inches. i. True ii. False
Explanation: Crate Volume: V = 288 cu. in × 20 V = 5760 cu. in Thus the statement is false.
Question 10. c. If the crate could hold 27 shoeboxes the volume of the crate would be about 7,776 cubic inches. i. True ii. False
Answer: True
Explanation: Crate Volume: V = 288 cu. in × 27 V = 7776 cu. in Thus the statement is true.

Question 11. Part B Mario claims that a rhombus is sometimes a square, but a square is always a rhombus. Is he correct? Explain your answer. i. yes ii. no
Explanation: A square is a quadrilateral with all sides equal in length and all interior angles right angles. A square however is a rhombus since all four of its sides are of the same length.

Explanation: Prism: In geometry, a prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first, and n other faces joining corresponding sides of the two bases. Figure B and C are prisms Pyramid: In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle called a lateral face. All the edges meet at the same point in the pyramid. Thus the figures A and D are pyramids.

Explanation: Mark packed 1-inch cubes into a box with a volume of 120 cubic inches. By seeing the figure we can say that there are 24 unit cubes. To find the number of layers we need to divide 120 by 24 = 120 ÷ 24 = 5 There are 5 layers of 1-inch cubes.

Answer: 312
Explanation: Split the figure into 2 parts. Figure 1: h = 3 cm w = 6 cm b = 4 cm V = 4 cm × 6 cm × 3 cm = 72 cu. cm Figure 2: b = 10 cm w = 6 cm h = 4 cm V = 10 cm × 6 cm × 4 cm = 240 cu. cm Now add the volume of 2 figures 72 cu. cm + 240 cu. cm = 312 cu cm Thus the volume of the composite figure is 312 cu. cm

Answer: rectangle
Explanation: Parallelograms are quadrilaterals with two sets of parallel sides. Since squares must be quadrilaterals with two sets of parallel sides, then all squares are parallelograms.

Answer: square
Explanation: A square is a quadrilateral with all sides equal in length and all interior angles right angles.

Answer: trapezoid
Explanation: A trapezoid has one pair of parallel sides and a parallelogram has two pairs of parallel sides. So a parallelogram is also a trapezoid.
Question 16. Megan’s aquarium has a volume of 4,320 cubic inches. Which could be the dimensions of the aquarium? Mark all that apply. Options: a. 16 in. by 16 in. by 18 in. b. 14 in. by 18 in. by 20 in. c. 12 in. by 15 in. by 24 in. d. 8 in. by 20 in. by 27 in.
Answer: C, D
Explanation: The volume of a prism = l × w × h 1. V = 16 in × 16 in × 16 in V = 4608 cu. in 2. V = 14 in × 18 in × 20 in = 5040 cu. in 3. V = 12 in × 15 in × 24 in = 4320 cu. in 4. V = 8 in × 20 in × 27 in = 4320 cu in Thus the suitable answers are C and D.
Question 17. Ken keeps paper clips in a box that is the shape of a cube. Each side of the cube is 3 inches. What is the volume of the box? ______ cubic inches
Explanation: Ken keeps paper clips in a box that is the shape of a cube. Each side of the cube is 3 inches. The volume of a cube = 3 in × 3 in × 3 in = 27 cu. in Therefore the volume of the box is 27 cubic inches.

Explanation: Monica used 1-inch cubes to make the rectangular prism Volume = 1 in × 1 in × 1 in = 1 cu. in. Each cube has a volume of 1 cubic inch.
Question 18. b. Each layer of the prism is made up of ____ cubes. ______ cubes
Explanation: We can calculate the layer by calculating the base and width 4 × 5 = 20 cubes Each layer of the prism is made up of 20 cubes.
Question 18. c. There are ____ layers of cubes. ______ layers
Answer: 3 By seeing the figure we can say that there are 3 layers of the cube. You can also find the layers of the cube by calculating the height of the figure.
Question 18. d. The volume of the prism is ____ cubic inches. ______ cubic inches
Explanation: The volume of a prism = l × w × h V = 4 in × 5 in × 3 in Volume = 60 cu. inches Therefore, the volume of the prism is 60 cubic inches.
Chapter Review/Test – Vocabulary – Page No. 4910

Question 1. A _____ has two congruent polygons as bases and rectangular lateral faces. __________
Answer: prism A prism has two congruent polygons as bases and rectangular lateral faces.
Question 2. A _____ has only one base and triangular lateral faces. __________
Answer: pyramid A pyramid has only one base and triangular lateral faces.

Answer: i. hexagon ii. regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure has six sides and 6 angles. Thus the name of the polygon is hexagon. Two polygons are congruent when they have the same size and the same shape. The above figure has same size and angles. Thus it is a regular polygon.

Answer: i. pentagon ii. regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure has five sides and 5 angles. Thus the name of the polygon is pentagon. Two polygons are congruent when they have the same size and the same shape. The above figure has same size and angles. Thus it is a regular polygon.

Answer: i. pentagon ii. not regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure has five sides and 5 angles. Thus the name of the polygon is the pentagon. Two polygons are congruent when they have the same size and the same shape. The above figure does not have the same size and angles. Thus it is not a regular polygon.

Answer: i. octagon ii. not regular
Explanation: A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure has 8 sides and 8 angles. Thus the name of the polygon is octagon. Two polygons are congruent when they have the same size and the same shape. The above figure does not have same size and angles. Thus it is not a regular polygon.
Classify each figure in as many ways as possible.

Answer: 1. quadrilateral 2. trapezoid
Explanation: 1. A general quadrilateral has 4 sides and 4 angles. 2. A trapezoid is a 4-sided flat shape with straight sides that has a pair of opposite sides parallel.

Answer: △ – scalene ∠ – right
Explanation: The above triangle has different sides. Thus the triangle is a scalene triangle. The triangle with one right angle is known as a right angled triangle.

Answer: prism
Explanation: In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.

Answer: pyramid
Explanation: In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point (the vertex). Like any pyramid, it is self-dual.

Explanation: The figure shows that there are 4 unit cubes.

Explanation: By seeing the above figure we can say that there are 7 unit cubes.

Explanation: The figure above shows that there are 5 unit cubes.

Answer: obtuse; scalene
Explanation: The sides of the triangle is different. Thus it is a scalene triangle. The angle of the triangle is an obtuse angle. Thus the correct answer is option C.

Answer: 7 faces, 12 edges, 7 vertices
Explanation: In geometry, a hexagonal pyramid is a pyramid with a hexagonal base upon which are erected six isosceles triangular faces that meet at a point. The hexagonal pyramid has 7 faces, 12 edges and 7 vertices. Therefore the correct answer is option C.
Question 16. A manufacturing company constructs a shipping box to hold its cereal boxes. Each cereal box has a volume of 40 cubic inches. If the shipping box holds 8 layers with 4 cereal boxes in each layer, what is the volume of the shipping box? Options: a. 160 cu in. b. 320 cu in. c. 480 cu in. d. 1,280 cu in.
Answer: 1,280 cu in.
Explanation: A manufacturing company constructs a shipping box to hold its cereal boxes. Each cereal box has a volume of 40 cubic inches. If the shipping box holds 8 layers with 4 cereal boxes in each layer Multiply the number of layers with boxes = 8 × 4 = 32 The volume of 8 layers is 40 × 32 = 1280 cubic inches Thus the correct answer is option D.
Question 17. Sharri packed away her old summer clothes in a storage tote that had a length of 3 feet, a width of 4 feet, and a height of 3 feet. What was the volume of the tote that Sharri used? Options: a. 36 cu ft b. 24 cu ft c. 21 cu ft d. 10 cu ft
Answer: 36 cu ft
Explanation: Given, Sharri packed away her old summer clothes in a storage tote that had a length of 3 feet, a width of 4 feet, and a height of 3 feet. Volume = l × w × h V = 3 ft × 4 ft × 3 ft V = 36 cu. ft Thus the volume of the tote that Sharri used is 36 cu. ft. The correct answer is option A.

Explanation: The opposite sides of figure b are not parallel. Thus the figure b quadrilateral is NOT classified as a parallelogram.

Answer: Volume of 1st cube is 5 cm × 4 cm × 5 cm = 100 cu. cm Volume of 2nd cube is 5 cm × 4 cm × 8 cm = 160 cu. cm Volume of 3rd cube is 5 cm × 4 cm × 5 cm = 100 cu. cm Add all the volumes to find the volume of the composite figure That means 100 cu. cm + 160 cu. cm + 100 cu. cm = 360 cu. cm Therefore the volume of the composite figure is 360 cm 3 The correct answer is option C.
Constructed Response

Answer: 512 cu. ft
Explanation: length = 2 ft width = 2 ft height = 2 ft Volume of the display of game console boxes = 2 ft × 2 ft × 2 ft = 8 cu. ft Number of console boxes = 64 64 × 8 cu. ft = 512 cu ft The volume of the display of game console boxes = 512 cu ft
Question 20. b. On a busy Saturday, the video game store sold 22 game consoles. What is the volume of the game console boxes that are left? _____ cu ft.
Answer: 336 cu. ft
length = 2 ft width = 2 ft height = 2 ft The volume of the display of game console boxes = 2 ft × 2 ft × 2 ft = 8 cu. ft Number of console boxes = 22 The volume of the game console boxes that are left 22 × 8 cu. ft = 176 cu. ft The volume of the game console boxes that are left = 512 – 176 = 336 cu. ft
Performance Task
Question 21. Look for two pictures of three-dimensional buildings in newspapers and magazines. The buildings should be rectangular prisms. A. Paste the pictures on a large sheet of paper. Leave room to write information near the picture. B. Label each building with their name and location. C. Research the buildings, if the information is available. Find things that are interesting about the buildings or their location. Also find their length, width, and height to the nearest foot. If the information is not available, measure the buildings on the page in inches or centimeters, and make a good estimate of their width (such as 1/2 the height, rounded to the nearest whole number). Find their volumes. D. Make a class presentation, choosing one of the buildings you found.
Conclusion:
Follow our Go Math Grade 5 Answer Key Chapter 11 Geometry and Volume to get the step by step explanation. So, Download the pdf of HMH Go Math 5th Grade Solution Key Chapter 11 Geometry and Volume for free. Click on the above links and find the question and answers with images. Do not move to anywhere, stay on Go Math, and follow them each and every question of Geometry and Volume with explanation and strengthen your math skills.
Share this:
Leave a comment cancel reply.
You must be logged in to post a comment.
- AP Calculus
- AP Statistics
- Independent Study
- Second Grade Math
- Third Grade Math
- Fourth Grade Math
- Fifth Grade Math
- Sixth Grade Math
- Sixth Grade Math (CA)
- Seventh Grade Math (CA)
- Eighth Grade Math (CA)
- Integrated Math 1
- Integrated Math 2
- Integrated Math 3
- PreCalculus
- AP Statistics Exam Prep
- Elementary Statistics
- ELM Practice
- Percents and Decimals
- Sixth Grade Math (Big Ideas)
Online Math Class
Mr. Math Blog
Polygons - Lesson 11.1
Triangles - Lesson 11.2
Quadrilaterals - Lesson 11.3
Three Dimensional Figures - Lesson 11.5
Unit Cubes and Solid Figures - Lesson 11.6
Understanding Volume - Lesson 11.7
Estimate Volume - Lesson 11.8
Volume of a Rectangular Prism - Lesson 11.9
Apply Volume Formulas - Lesson 11.10
Finding Volume of Composite Formulas - Lesson 11.12
Find a Part of a Group - Lesson 7.1
Multiply Fractions and Whole Numbers - Lesson 7.2
Fraction and Whole Number Multiplication - Lesson 7.3
Multiply Fractions - Lesson 7.4
Compare Fraction Factor and Product - Lesson 7.5
Fraction Multiplication - Lesson 7.6
Area and Mixed Numbers - Lesson 7.7
Compare Mixed Number Factors and Products - Lesson 7.8
Multiply Mixed Numbers - Lesson 7.9
Problem Solving - Find Unknown Lengths - Lesson 7.10
Please Donate, if you're a regular!
The donate link is below. Thanks so much!!
Line Plots - Lesson 9.1
Ordered Pairs - Lesson 9.2
Graph Data - Lesson 9.3
Line Graphs - Lesson 9.4
Numerical Patterns - Lesson 9.5
Problem Solving - Find a Rule - Lesson 9.6
Graph and Analyze Relationships - Lesson 9.7
Customary Length - Lesson 10.1
Customary Capacity - Lesson 10.2
Weight - Lesson 10.3
Multistep Measurement Problems - Lesson 10.4
Metric Measures - Lesson 10.5
Problem Solving Conversions - Lesson 10.6
Elapsed Time - Lesson 10.7
Division Patterns with Decimals - Lesson 5.1
Divide Decimals by Whole Numbers - Lesson 5.2
Estimate Quotients - lesson 5.3
Division of Decimals by Whole Numbers - Lesson 5.4
Decimal Division - Lesson 5.5
Divide Decimals - Lesson 5.6
Write Zeros in the Dividend - Lesson 5.7
Problem Solving - Decimal Operations - Lesson 5.8
Divide Fractions and Whole Numbers - Lesson 8.1
Problem Solving - Use Multiplication - Lesson 8.2
Connect Fractions to Division - Lesson 8.3
Fraction and Whole Number Division - Lesson 8.4
Interpret Division with Fractions - Lesson 8.5
Addition with Unlike Denominators - Lesson 6.1
Subtraction with Unlike Denominators - Lesson 6.2
Estimate Fraction Sums and Differences - Lesson 6.3
Common Denominators and Equivalent Fractions - Lesson 6.4
Add or Subtract Fractions - Lesson 6.5
Add or Subtract Mixed Numbers - Lesson 6.6
Subtraction with Renaming - Lesson 6.7
Patterns with Fractions - Lesson 6.8
Problem Solving with Addition and Subtraction - Lesson 6.9
Use Properties of Addition - Lesson 6.10
Multiplication Patterns with Decimals - Lesson 4.1
Multiply Decimals and Whole Numbers - Lesson 4.2
Multiply Decimals and Whole Numbers - Lesson 4.3
Multiply Using Expanded Form - Lesson 4.4
Problem Solving - Multiply Money - Lesson 4.5
Decimal Multiplication - Lesson 4.6
Multiply Decimals - Lesson 4.7
Thousandths - Lesson 3.1
Place Value of Decimals - Lesson 3.2
Compare and Order Decimals - Lesson 3.3
Round Decimals - Lesson 3.4
Decimal Addition - Lesson 3.5
Decimal Subtraction - Lesson 3.6
Estimate Decimal Sums and Differences - Lesson 3.7
Add Decimals - Lesson 3.8
Subtract Decimals - Lesson 3.9
Patterns with Decimals - Lesson 3.10
Problem Solving Add and Subtract Money - Lesson 3.11
Choose a Method - Lesson 3.12
Performance Task on Chapter 3
Place the First Digit - Lesson 2.1
Divide by 1-Digit Divisors - Lesson 2.2
Division with 2-Digit Divisors - Lesson 2.3
Partial Quotients - Lesson 2.4
Estimate with 2-Digit Divisors - Lesson 2.5
Divide by 2-Digit Divisors - Lesson 2.6
Interpret the Remainder - Lesson 2.7
Adjust Quotients - Lesson 2.8
Problem Solving - Division - Lesson 2.9
Performance Task on Chapter 2
Fifth Grade
Math
Copyright 2013. All rights reserved.
An Introduction to Relational Frame Theory (Standard)
11.10 combining many stimulus relations part 1.
Also, combinatorial entailment can involve combining more than just two stimulus relations. For example, if we added these contextual cues and triangles to our special triangle sorting game…
Leave a Comment Cancel reply
You must be logged in to post a comment.
Lesson Plan: Solving Percent Problems and Using Proportional Reasoning
This lesson plan is designed for two 50-minute class periods.

Lesson Objectives
- Solve various types of percent problems
- Use proportional relationships in percent calculations
- Apply percent concepts to financial situations
- Compare simple and compound interest
TEKS Standards
- 8.4D: Use proportional relationships to solve multi-step ratio and percent problems.
- 8.5A: Represent linear proportional situations with tables, graphs, and equations.
- 8.5E: Solve problems using direct variation.
- 8.12D: Calculate and compare simple interest and compound interest earnings.
Prerequisite Skills
- Understanding of percents
- Basic algebra skills
- Knowledge of square roots and cube roots
- Understanding of ratios and proportions
Key Vocabulary
- Irrational number
- Square root
- Rational approximation
- Scale model
Warm-up Activity (10 minutes)
Review strategies for the following percent calculations:
- Percent of a number: https://www.media4math.com/library/64365/asset-preview
- Find the whole given the percent: https://www.media4math.com/library/64368/asset-preview
- The percent one number is of another: https://www.media4math.com/library/75772/asset-preview
Teach (70 minutes)
Definitions .
- Percent : A ratio that compares a number to 100
- Markup : An increase in the price of a product
- Markdown : A decrease in the price of a product
- Commission : A fee paid to an agent or employee for conducting a transaction
- Interest : Money paid regularly at a particular rate for the use of borrowed money
- Irrational number : A number that cannot be expressed as a simple fraction
- Square root : A value that, when multiplied by itself, gives the number
- Cube root : A value that, when multiplied by itself twice, gives the number
- Rational approximation : An estimate of an irrational number using a ratio of integers
- Scale model : A representation of an object that is larger or smaller than the actual size
You can also use this slide show of definitions, which include examples of the relevant term:
https://www.media4math.com/library/slideshow/definitions-solving-percent-problems
Instruction
Demonstrate how to set up proportions to solve problems. Use this slide show to review examples of solving different proportions:
https://www.media4math.com/library/slideshow/math-examples-solving-proportions-algebraically
Use this slide show to give an overview of percents:
https://www.media4math.com/library/slideshow/overview-percents
Next, review these examples.
Example 1: Markup Problem
A store buys a jacket for $80 and wants to mark it up by 45%. What should the selling price be?
| 1. Set up the proportion: | 45/100 = x/80 |
| 2. Cross multiply: | 45 * 80 = 100x |
| 3. Solve for x: | x = (45 * 80) / 100 = 36 |
| 4. The markup amount is | \$36 |
| 5. Add the markup to the original price: | \$80 + \$36 = \$116 |
The selling price should be \$116.
Example 2: Commission Problem
A real estate agent earns a 6% commission on home sales. If they sell a house for \$250,000, how much commission will they earn?
| 1. Set up the proportion: | 6/100 = x/250,000 |
| 2. Cross multiply: | 6 * 250,000 = 100x |
| 3. Solve for x: | x = (6 * 250,000) / 100 = 15,000 |
The agent will earn \$15,000 in commission.
Example 3: Approximating Irrational Numbers
Approximate √20 to the nearest tenth and express it as a ratio.
| 1. Find the perfect squares on either side of 20: | 16 (4 ) and 25 (5 ) |
| 2. √20 is between | 4 and 5 |
| 3. Use a calculator to find | √20 ≈ 4.472135... |
| 4. Round to the nearest tenth: | √20 ≈ 4.5 |
| 5. Express as a ratio: | 45:10 or 9:2 |
Example 4: Scale Model Problem
An architect is creating a scale model of a building. The actual building is 45 meters tall, and in the model, it is 15 centimeters tall. If a window on the model is 2 centimeters tall, how tall is the actual window?
| 1. Set up the proportion: | 15 cm / 45 m = 2 cm / x m |
| 2. Convert 45 m to cm: | 45 m = 4500 cm |
| 3. Rewrite the proportion: | 15 / 4500 = 2 / x |
| 4. Cross multiply: | 15x = 2 * 4500 |
| 5. Solve for x: | x = (2 * 4500) / 15 = 600 |
| 6. Convert 600 cm to meters: | 600 cm = 6 m |
The actual window is 6 meters tall.
Example 5: Carbon Dating
Use this slide show to introduce an application of proportional reasoning in the context of carbon dating:
https://www.media4math.com/library/slideshow/applications-proportional-reasoning-carbon-dating
This table summarizes the data:
| 1 | 1.00 • 10 | -- |
| 1 | 5.00 • 10 | 5730 |
| 1 | 2.50 • 10 | 11,460 |
| 1 | 1.25 • 10 | 17,190 |
| 1 | 6.25 • 10 | 22,920 |
| 1 | 3.13 • 10 | 28,650 |
| 1 | 1.56 • 10 | 34,380 |
| 1 | 7.81 • 10 | 40,110 |
| 1 | 3.91 • 10 | 51,570 |
Make a note of the changing ratios. With each subsequent ratio, the number in scientific notation is reduced by 50% and the age of the artefact is an additional 5730 years old.
Review (30 minutes)
Refer to the following videos to review key concepts:
- Calculating Tips and Commissions: https://www.media4math.com/library/1819/asset-preview
- Calculating Tax: https://www.media4math.com/library/1818/asset-preview
- Percent Increase: https://www.media4math.com/library/1815/asset-preview
- Percent Decrease: https://www.media4math.com/library/1816/asset-preview
Assess (10 minutes)
Administer this 12-question quiz.
Quiz Questions
- A store buys a television for $400 and marks it up by 35%. What is the selling price?
- A real estate agent earns a 5.5% commission on a house sale. How much will they earn if the house sells for $280,000?
- Approximate √18 to the nearest tenth and express your answer as a ratio.
- An architect's scale model has a 1:150 ratio. If a door in the model is 3 cm tall, how tall is the actual door?
- A shirt originally priced at $50 is on sale for 20% off. What is the sale price?
- If the population of a city increased from 50,000 to 57,500, what was the percent increase?
- A car's value depreciates from $25,000 to $21,250 after one year. What is the percent decrease?
- Estimate √8 by finding two perfect squares it falls between, then narrow it down to a range of tenths.
- A salesperson earns an 8% commission. How much will they earn on a $1500 sale?
- In a scale model, 2 cm represents 5 m. How many centimeters would represent 12.5 m?
- Approximate π to two decimal places and express your answer as a ratio.
- Which is greater: √13 or 3.7? Justify your answer using rational approximations.
- The square root is between 4 and 4.3. A reasonable estimate is 4.2. As a ratio, it's expressed as 42:10 or 21:5.
- 4.5 m or 450 cm
- 2.8 < √8 < 2.9 (between 2^2=4 and 3^2=9)
- 314:100 or 157:50
- √13 is greater. 3.6^2 = 12.96, 3.7^2 = 13.69, so 3.6 < √13 < 3.7

Communication Life Hacks
About the store, featured resources.

SUPER BUNDLE Problem Solving for Middle and High Schoolers lessons 1-16

SEL Problem Solving Lessons For Middle and High Schoolers Lessons 9-16 Bundle

SEL Problem Solving Lessons For Middle and High Schoolers Lessons 1-8 Bundle
Store categories, all resources.
- Best Sellers
- Price (Ascending)
- Price (Descending)
- Most Recent
Resource Type

SEL problem solving visual with a catchy acronym for Middle and High Schoolers
Teaching style.
- We're hiring
- Help & FAQ
- Privacy policy
- Student privacy
- Terms of service
- Tell us what you think

IMAGES
VIDEO
COMMENTS
This Go Math video covers the topic of finding varied combinations of rectangular prisms, but learning how they will all have the same volume. Students will ...
This video covers Lesson 11.10 Problem Solving-Compare Volumes on pages 503-506 of the 5th grade GO Math textbook.
NameProblem Solving • Compare VolumesLesson 11.10Essential Question: How can you use the strategy make a table to comp. Measurement and Data—. 5.MD.C.5bMATHEMATICALMP1. Unlock l t the Problem lAdam has 50. w many rectangular prisms, each with a different-sizeba. e, that he could make with all of the one-inch cubes.Use the.
Volume is the number of cubic units we need to fill a three-dimensional space. We use length, width, and height as factors to find volume. We can use the str...
UNLOCK the Problem - Lesson 8: Volume of Rectangular Prisms - Page No. 684; Lesson 9: Algebra Apply Volume Formulas. Share and Show - Lesson 9: Algebra Apply Volume Formulas - Page No. 689; Problem Solving - Lesson 9: Algebra Apply Volume Formulas - Page No. 690; Lesson 10: Problem Solving Compare Volumes
Make a table to help you solve each problem. PROBLEM SOLVING Lesson 11.11 COMMON CORE STANDARD CC.5.MD.5b Geometric measurement: understand concepts of volume and relate volume to multiplication ... (Lesson 11.9) @ 11 m3 @ 18m3 36 m3 @ 360 m3 . Title: Print Author: Dan Created Date:
Go Math! What is the "Go Math!" curriculum? Curriculum - This details what domain, cluster, standard, and essential questions are taught within the math program. In addition, it informs the parent what other interdisciplinary standards (technology, science, social studies, and literacy) are incorporated in each domain.
The Chapter 11 Resource Masters includes the core materials needed for Chapter 11. These materials include worksheets, extensions, and assessment options. The answers for these pages appear at the back of this booklet. All of the materials found in this booklet are included for viewing and printing in the.
Lesson 9.6 Problem Solving Find a Rule Lesson 9.7 Graph & Analyze Relationships Coordinate Grid Practice Games 10. Convert Units of Measure Lesson 10.1 Customary Length Lesson 10.2 Customary Capacity Lesson 10.3 Weight Lesson 10.4 Multi-Step Measurement Problems Lesson 10.5 Metric Measures Lesson 10.6 Problem Solving Lesson 10.7 Elapsed ...
Lesson 11.10 Common core COMMON CORE STANDARD—3.MD.D.8 Geometric measurement: recognize perimeter as an attribute ofplane figures and distinguish between linear and area measures. 8 square units 18 units as a greater perimeter. A: Perimeter B: Area — Perimeter Rectangle has a greater perimeter. Beth's Tile Designs 685 eal Problem Solving
Patterns with Decimals - Lesson 3.10. Problem Solving Add and Subtract Money - Lesson 3.11. Choose a Method - Lesson 3.12. Performance Task on Chapter 3. Place the First Digit - Lesson 2.1. Divide by 1-Digit Divisors - Lesson 2.2. Division with 2-Digit Divisors - Lesson 2.3.
Problem Solving -Compare Volumes
An Introduction to Relational Frame Theory (Standard) Lesson 11: Combinatorial Entailment 11.10 Combining Many Stimulus Relations Part 1. This is the open-access version of this module and your progress is not tracked or recorded. Also, combinatorial entailment can involve combining more than just two stimulus relations. For example, if we ...
Lesson 11.1 Model Perimeter Lesson 11.2 Find Perimeter . Leeson 11.3 Algebra-Find unknown side lengths . Lesson 11.4 Understand Area . Lesson 11.5 Measure Area . ... Problem Solving Area of Rectangles Mrs. Wilson wants to plant a garden, so she drew plans for some sample gardens. She wants to know how the areas of the gardens are
Go-Math Grade 3 Chapter 11 Lesson Plans (Lessons 11.1 - 11.10 with Journal Prompts & Vocabulary). Lesson Topics Included in the Bundle: • Investigate-Model Perimeter • Find Perimeter • Algebra - Find Unknown Side Lengths • Understand Area • Measure Area • Use Area Models • Problem Solving - Areas of Rectangles • Area of ...
PROBLEM SOLVING Chapter 11 P207 An artist makes rectangular murals in different sizes. Below are the available sizes. Each unit square is 1 square meter. ... Problem Solving • Area of Rectangles Lesson 11.7 Mural Length (in meters) Width (in meters) Area (in square meters) A 21 B 2 C 2 D 2 2 4 2 COMMON CORE STANDARD— 3.MD.7b
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket Press Copyright ...
Lesson Plans: Ratios (Gr 8--TEKS) Lesson Plan Library; Lesson Plan 1: Ratios and Proportional Relationships; Lesson Plan 2: Solving Percent Problems; Lesson Plan 3: Graphing and Interpreting Proportional Relationships; Lesson Plan 4: Direct Variations; Lesson Plan 5: Parallel and Perpendicular Lines
Solving Rational Equations. 1. Cross Multiply. 2. Or use Quadratic Formula: x= −b ± √b²−4ac/2a. 3. ALWAYS plug in the answer (s) to the original equation to make sure it works. There may be one answer or two and/or NO SOLUTION (∅) Study with Quizlet and memorize flashcards containing terms like 11-1 Inverse Variation, 11-2 Rational ...
Study with Quizlet and memorize flashcards containing terms like Effective problem solving involves developing a _____ and _____ the plan., Your textbook teaches a _____ - step approach to numeric problem solving., Step 1 is to _____ the problem. and more.
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket Press Copyright ...
MIST lessons teach each letter in the acronym along with the foundational self-regulation and problem solving skills. When . 8. Products. $10.00 Price $10.00 $16. ... That is why the Mindfulness and I statement steps are so important. When starting as an SLP, my problem solving lessons focused on thinking of Solutions to problems. I did not ...