problem solving percentages year 5

5th Grade Percentage Worksheet

In 5th grade percentage worksheet, students can practice the questions on percentage . The questions are based on convert percentages to fractions , convert percentages to decimals, convert fractions to percentages, convert decimals to percentages, find the percentage of a number and word problems on percentage.

1.  Convert the following percentages to fraction.

2. Convert the following percentages to decimals.

3. Convert the following fractions to percentages.

(i) \(\frac{3}{10}\)

(ii) \(\frac{7}{20}\)

(iii) \(\frac{23}{25}\)

(iv) \(\frac{34}{50}\)

(v) \(\frac{3}{4}\)

4. Convert the following decimals to percentage.

5. Find the value of the following:

(i) 10% of 90 g

(ii) 75% of 6 l

(iii) 13% of 250 km

(iv) 73% of 204

(v) 41% of $800

(vi) 22% of 138

6. What is 70% of a kg?

7.  What percent of 20 is 15?

8.  What percent of 40 is 14?

9.  In the set of first 10 natural numbers – 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10:

(i) What percent of the numbers are odd?

(ii) What percent of numbers are multiples of 4?

(iii) What percent of numbers are less than 8?

(iv) What percent of numbers are factors of 7?

10. Angela loves to travel and spends 25% of the year on vacation and works for the rest of the year. What fraction of the year does she travel?

11. The cost price of an article is $400 and selling price of the same article is $500. At what profit is the article sold? What is the profit percentage?

12.  1200 people registered for the Marathon but only 960 runners actually ran. What percentage of the registered people ran the Marathon?

13.  In a flower vase there are 20 flowers. There are 5 lilies and 15 roses. What percent of flowers are lilies?

1. (i) \(\frac{7}{100}\)

(ii) \(\frac{55}{100}\)

(iii) \(\frac{20}{100}\)

(iv) \(\frac{2.5}{100}\)

2. (i) 0.08

(iii) 32.5 km

(iv) 148.92

7.  75%

8.  35%

9.  (i) 50%

10.  91\(\frac{1}{4}\)

11.  $100, 25%

12.  80%

13.  25%

5th Grade Numbers Page 5th Grade Math Problems 5th Grade Math Worksheets From 5th Grade Percentage Worksheet to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

Share this page: What’s this?

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

2nd Grade Math Practice | Second Grade Math |2nd Grade Math Worksheets

Nov 18, 24 02:23 PM

2nd Grade Measurement Worksheets | Measuring Length, Mass and Volume

Nov 18, 24 02:19 PM

Worksheet on Addition of Length | Word Problems on Addition of Length

Nov 17, 24 10:29 PM

Worksheet on Addition of Mass | Word problems on Addition of Mass

Nov 17, 24 10:26 PM

Worksheet on Addition of Capacity | Word Problems on Adding capacity

Nov 17, 24 10:19 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Mastery-Aligned Maths Tutoring

“The best thing has been the increase in confidence and tutors being there to deal with any misunderstandings straight away."

FREE daily maths challenges

A new KS2 maths challenge every day. Perfect as lesson starters - no prep required!

25 Percentage Word Problems For Year 5 To Year 8 With Tips On Supporting Pupils’ Progress

Emma Johnson

Percentage word problems and the concept of calculating percentages first appears in Upper Key Stage 2. As pupils progress through school from KS2 to KS3, the skills they need to solve percentage word problems develop.

It is important to expose students to percentage word problems alongside any fluency work on percentages, to help them understand how percentages are used in real-life. To help you with this, we have put together a collection of 25 percentage word problems which can be used by pupils from Year 5 to Year 8. Don’t miss our downloadable word problems worksheet to develop these skills further!

How pupils develop the necessary skills to solve percentage word problems

Percentage word problems in the national curriculum.

• Why are word problems important for children’s understanding of percentage 

How to teach solving percentage word problems in KS2 and early KS3

Percentage word problems for year 5, percentage word problems for year 6, percentage word problems for key stage 3, more word problems resources, percentage word problems faqs.

All Kinds of Word Problems Four Operations

Download this free, printable pack of word problems covering all four operations; a great way to build students' problem solving skills.

Initially, pupils are introduced to the per cent symbol (%) in Year 5. At this stage they are expected to understand that percent relates to ‘number of parts per hundred’ and should be able to solve problems requiring knowing percentage and decimal form equivalents of simple fractions.

As pupils progress into Year 6, they should be able to recall and use equivalences between simple fractions, mixed numbers, decimals and percentages. They also need to be able to solve word problems involving percentages of amounts and percentage increase and decrease.

Moving into Key Stage 3, pupils continue to build on the percentage work from primary, to solve percent problems, interpreting percentages and percentage change; expressing one quantity as a percentage of another; comparing two quantities using percentages and working with percentages greater than 100%.

Concrete resources (such as percentages cubes) and visual images (such as bar models) are important during the early stages of learning and understanding percentages. Word problems for year 3 and word problems for year 4 will often include visual aids. Upper Key Stage 2 teachers and pupils often have the mistaken belief that concrete resources are only for children who are struggling; however, with a new topic, such as percentages, it is important all children are initially introduced to the topic through the use of visual and concrete aids.

Children are first introduced to percentage problems in Year 5. The National Curriculum expectations for percentages are that children will be able to:

Percentage in Year 5

• Recognise the percent symbol (5)  and understand that per cent relates to ‘number of parts per hundred’.
• Write percentages as a fraction with a denominator 100, and in its decimal form.
• Solve problems which require knowing percentage and decimal equivalents of \frac{1}{2},\frac{1}{4},\frac{1}{5},\frac{2}{5},\frac{4}{5} , and fractions with a denominator of a multiple of 10 or 25.

Percentage in Year 6

• Recall and use equivalences between simple fractions, decimals and percentages, including in different contexts.
• Solve problems involving the calculation of percentages (for example, measures and such as 15% of 360) and use percentages for comparison.

Percentage in Key Stage 3

• Define percentage as ‘number of parts per hundred’
• Interpret percentages and percentage changes as a fraction or a decimal. Interpret these multiplicatively.
• Express one quantity as a percentage of another.
• Compare two quantities using percentages.
• Work with percentages greater than 100%.
• Interpret fractions and percentages as operators.

Percentage word problems will often include other skills, such as fraction word problems , multiplication word problems , addition word problems , subtraction word problems and division word problems .

Why are word problems important for children’s understanding of percentage 

Percentage word problems help children to develop their understanding of percentages and the different ways percentages are used in everyday life. Taken out of context, percentages can be quite an abstract concept, which some children can find quite difficult to understand. 

Real-life problems involving percentages enable students to see how they will make use of this key skill outside the classroom.

As with all word problems, students need to learn the skills required to solve percentage word problems. It’s important that children make sure they have read the questions carefully and thought about exactly what is being asked and whether they have fully understood this. They then need to identify what they will need to do to solve the problem and whether there are any concrete resources or pictorial representations which they can use to help them. Even pupils in Key Stage 3 can benefit from drawing a quick picture, to understand what a word problem is asking.

Third Space Learning’s online, one-to-one tutoring programmes work to build students’ maths fluency and reasoning skills. Personalised to the needs of each individual student, our programmes fill gaps and build students’ confidence in maths.

Percent word problem example :

A box of cupcakes sold by a bakery cost £3.40.

Due to the increased costs involved with running a bakery, the owner has decided to increase the price of everything sold by 20%.

How much will a box of cupcakes cost once the price has been increased?

How to solve step-by-step:

What do you already know?

–        We know that the original price of a box of cupcakes is £3.40.

–        If the price of the box is being increased by 20%, we need to work out how much 20% of £3.40 is.

–        To do this, we need to work out how much 10% of £3.40 is. We therefore need to divide £3.40 by 10 = £0.34

–        To calculate what 20% is, we need to multiply the £0.34 by 2 = £0.68

–        Finally, we need to add the 20% (£0.68) onto the original price.

–        £3.40 + £0.68 = £4.08

How can this be represented pictorially?

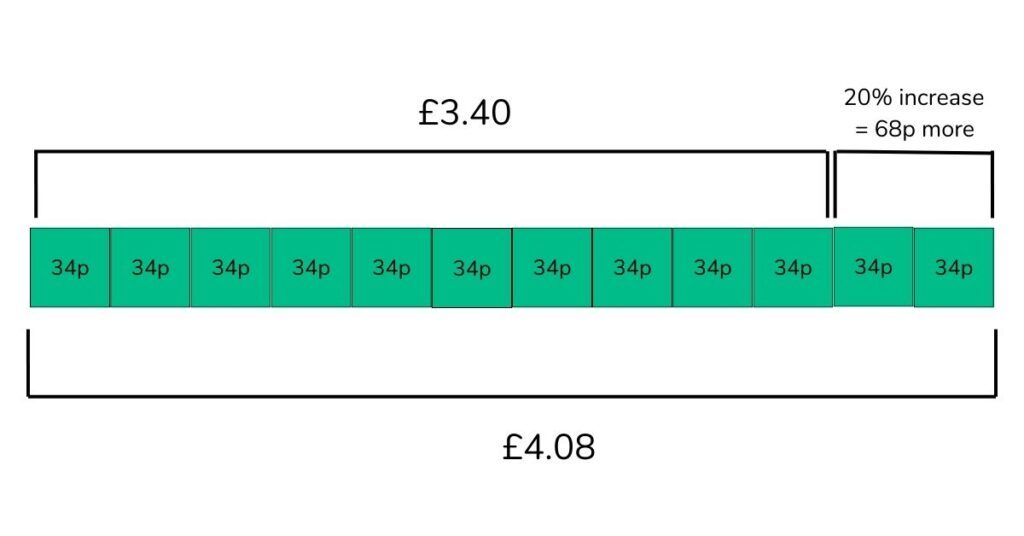
• We can draw a bar model to represent what 10% of £3.40 equals.
• Once we know what 10% of £3.40 is (34p), we can double it to calculate 20% of £3.40 (68p).
• We can then add this on to the original price of £3.40.
• £3.40 + 68p = £4.08.

To solve word problems for year 5 , children need to be able to convert fractions to percentages and calculate fractions of an amount.

Gemma saves \frac{1}{2} of her pocket money every week.

She receives £5 per week and is saving to buy a game costing £25.

• What percentage does she save each week?
• How long will it take her to save for the game?
• She saves 50% of her pocket money each week

Gemma saves £2.50 per week.

£2.50 x 10 = £25

Sam gives \frac{4}{10} of his sweets to Ahmed.

What percentage of the sweets does he keep for himself?

Answer : 60%

  \frac{4}{10} =  \frac{40}{100} = 40%

100 – 40 = 60%

A school football team has 11 players and 5 substitutes.

  \frac{3}{4} of the players are boys, the rest are girls.

What percentage are girls?

Answer: 25%

\frac{3}{4} of 16 are boys

  \frac{1}{4} are girls

  \frac{1}{4} = 25%

Children in Year 5 voted on their favourite food.

35% of children voted for pizza.

60 children took part in the survey.

How many voted for pizza?

Answer : 21 children 

10% of 60: 60 ÷ 10 = 6

5% of 60: Half of 10% (6) = 3

30%: 6 x 3 = 18

35% = 18 + 3 = 21

Ben was given a maths worksheet to complete for his homework.

He got  \frac{6}{10} of the maths problems correct

If there were 20 questions on the paper:

• How many questions did he get right?
• What percentage did he score?

  \frac{1}{10} of 20  = 2

  \frac{6}{10} of 20  = 12

• 60% correct

  \frac{12}{20} =  \frac{60}{100} .

An ice cream seller has been researching the most popular ice creams.

He knows the percentage of each flavour of ice cream sold, but wants to work out how many of each flavour were sold.

80 ice creams were sold in total.

40% vanilla

25% strawberry

20% cookie dough

15% mint choc chip

How many of each ice cream flavour were sold?

20 strawberry

16 cookie dough

12 mint choc chip

10% of 80 = 8 ice creams

5% of 80 = 4 ice creams

Vanilla: 4 x 8 = 32

Strawberry: 2 x 8 = 16. 16 + 4 = 20

Cookie dough: 2 x 8 = 16

Mint choc chip: 8 + 4 = 12

Pupils in Year 5 held a vote on where to go for their next school trip.

The vote was between the zoo and the aquarium.

90 children voted. 

40% voted for the zoo

How many pupils voted for the aquarium?

Answer : 54 children

60% voted for the aquarium

10% of 90 = 9 children

60% = 6 x 9 = 54 children

The price of burgers being sold by a burger van have increased by 25%

If the original price was £2 per burger. How much are the burgers now?

Answer : £2.50

25% of £2 = £2 ÷ 4 = 50p

£2 + 50p = £2.50

Word problems for year 6 involve solving problems involving equivalence between fractions, decimals and percentages; calculation of percentages and using percentages for comparison. Year 6 students will also tackle multi-step problems .

A rugby game lasts for 80 minutes.

A player is on the pitch for 85% of the game.

How long is he on the pitch for?

Answer : 68 minutes

10% of 80  = 8 minutes

5%  = Half of 8 minutes = 4 minutes

80% = 8 x 8 = 64 minutes

64 + 4 = 68 minutes

There are 480 pupils in a primary school.

15% in foundation

25% in Key Stage 1

How many pupils are in Key Stage 2?

Answer : 288 pupils

In foundation there are 15% + 25% (40% of the pupils)

Therefore, 60% of pupils are in KS2

10% of 480 = 48 pupils

60% = 6 x 48 = 288 pupils

A pizza restaurant decided to add a 15% increase to the cost of all their pizzas.

The cost of a meat feast pizza before the increase was £12.60

What is the new price of the pizza?

Answer : £14.49

10% of £12.60 = £1.26

5% = Half of £1.26 = £0.63

15% = £1.26 + £0.63 = £1.89

New price: £12.60 + £1.89 = £14.49

Oliver was shopping for a new pair of jeans.

The jeans were 15% off  in the sale, but the new sale price sticker had fallen off.

The original price of the jeans was £35.

How much did they cost in the sale?

Answer : £29.75

10% of £35 = £3.50

5% = Half of £3.50 = £1.75

35% = £3.50 + £1.75 = £5.25

New price: £35 – £5.25 = £29.75

200g of sugar is needed for a chocolate brownies recipe.

A 1kg bag of sugar is used.

25% of the remaining sugar is used to bake a cake too.

How much sugar was used to bake the cake?

Answer : 200g sugar

 200g sugar used for brownies, therefore 1000g – 200g = 800g remaining

25% of 800g = 800 ÷ 4 = 200g

Mr Jones bought a second hand car for £12,400

A year later, it had decreased in value by 15%

What was the value of the car after a year?

Answer : £10,540

10% of 12,400 = £1,240

5%  = half of £1240 = £620

15% = 1240 + 620 = £1,860

Value after a year = 12,400 – 1860 = £10,540

The number of visitors to a theme park in 2021 was 286,000.

The following year, there was a 24 percent increase in visitors.

How many visited the theme park in 2022?

Answer : 354,640 visitors

10% of 286,000 = 28,600

20% = 2 x 28,600 = 57,200

1% of 286,000 = 2,860

4% = 4 x 2860 = 11,440

24% = 57,200 + 11,440 = 68.640

Total number of visitors: 286,000 + 68,640 = 354,640

A library has 16,200 books

55% are fiction and 45% are non-fiction

968 non-fiction books are taken out in one week.

How many non-fiction books are left in the library, from the books which were there at the start of the week? 

Answer : 6,322 non-fiction books

10% of 16,200 = 1,620

40% = 1,620 x 4 = 6,480 books

5% = half of 1,620 = 810

45% = 6,480 + 810 = 7,290

7,290 – 968 = 6,322

In Key Stage 3, the work pupils carry out on percentages, builds upon the percentage skills developed in primary. Students need to be able to solve percent word problems involving interpreting percentages and percentage change as a fraction or decimal; expressing one quantity as a percentage of another; comparing two quantities using percentages; working with percentages greater than 100% and interpreting fractions and percentages as operators.

Jasmine wins £600

She gives 30% to her sister and 20% to her friend.

She keeps the rest.

How much does each person have?

Sister: £180

Friend: £120

Jasmine: £300

She gives 30% to her sister.

10% of £600 = £60

30% = 3 x 60 = £180

She gives 20% to her friend.

20% = 2 x 60 = £120

She must keep 50% for herself, if she has given 30% and 40% away.

50% of 600 =  \frac{1}{2} of 600 = £300

A car is reduced in the sale by 15%

If the original price was £18,500, what is the price of the car now?

Answer: £16,225

10% of 18500 = 1,850

5% = half of 1,850 = £925

15% = 1,850 + 925 = £2,275

New price: 18,500 – 2,275 = £16,225

Sales tax in Florida is 6%

Maisie has bought a pair of jeans, 3 T shirts and a jacket, which came to $150

How much will she have to pay, once she has added on the sales tax?

Answer: $159

1% of 150 = 1.5

6% = 6 x 1.5 = $9

150 + 9 = $159

A packet of biscuits is 300g

As a special offer, the biscuits currently have an extra 15% free.

How many grams of biscuit do you get with the special offer?

Answer : 345g

10% of 300 = 30g

5% = half of 30 = 15g

15% = 30 + 15 = 45g

New weight: 300 + 45 = 345g

Jason is travelling to Birmingham from Manchester.

His average speed is 62 miles per hour

On the return journey, the traffic on the M6 is terrible and his average speed it reduced by 35%

What is his average speed on the return journey?

Answer : 40.3mph

10% of 62 = 6.2mph

30% = 6.2 x 3 = 18.6mph

5% = half of 6.2 = 3.1mph

35% = 18.6 + 3.1 = 21.7mph

62 – 21.7 = 40.3 mph

Mr Andrews bought a car in January 2021 for £15000.

By January 2022 his car had depreciated in value by 20%.

By January 2023, his car had depreciated in value by another 30%.

What was the value of his car in January 2023?

Answer : £8400

January 2022

20% of £15000 = £3000, so the value of the car is £12000.

January 2023

30% of £12000 = £3600, so the value of the car is £8400.

Alternative method – using decimal multiplier

20% decrease means 80% of January 2021 value – decimal multiplier of 0.8

30% decrease means 70% of January 2022 value – decimal multiplier of 0.7

15000 x 0.8 x 0.7 = £8400.

In her half term test, Jasmine did a French test and scored 15 out of 30.

In her next half term test, Jasmine scored 21 out of 30 in her French test.

By what percentage did Jasmine improve?

Answer : 40% improvement

Percentage change

= 21 – 15/15  x 100

= 6/15  x 100 = 40% improvement.

In 2021, a company made a profit of $600000.

In 2022, the same company made a profit of $1350000.

By what percentage had their profit increased?

Answer : 125% improvement

= 1350000 – 600000/600000 x 100

= 750000/600000 x 100 = 125% improvement.

In 2022, Thomas earned £1800 a month for his job.

As part of his annual review in February 2023, he is going to ask for a pay rise of 3.5%.

If the pay rise is agreed, what will Thomas’ annual salary be?

Answer: £22356

3.5% of £1800 = £63

So new monthly salary would be £1863

£1863 x 12 = £22356.

Alternative method 1

£1800 x 12 = £21600

3.5% of £21600 = £756

£21600 + £756 = £22356.

Looking for more word problems practice questions? Take a look at our collection of addition and subtraction word problems , time word problems , money word problems and ratio word problems . Teaching percentages to KS3 or KS4? Check out our percentage worksheets here.

There are different types of percentage problems. If you want to find the percentage of an amount, it can be calculated by writing the percentage as a decimal or a fraction and then multiplying it by the amount.

Pupils in Year 5 held a vote on where to go for their next school trip. The vote was between the zoo and the aquarium. 90 children voted.  40% voted for the zoo How many pupils voted for the aquarium?

1. Calculating a discount when shopping 2. Understanding bank interest rates 3. Understanding your grades in school

DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to one lessons have helped over 169,000 primary and secondary students become more confident, able mathematicians.

Learn how tutors develop pupils’ maths fluency or request a personalised quote for your school to speak to us about your school’s needs and how we can help.

Related articles

Maths Problem Solving: Engaging Your Students And Strengthening Their Mathematical Skills

Free Year 7 Maths Test With Answers And Mark Scheme: Mixed Topic Questions

What Is A Number Square? Explained For Primary School Teachers, Parents & Pupils

What Is Numicon? Explained For Primary School Teachers, Parents And Pupils

FREE Guide to Maths Mastery

All you need to know to successfully implement a mastery approach to mathematics in your primary school, at whatever stage of your journey.

Ideal for running staff meetings on mastery or sense checking your own approach to mastery.

Privacy Overview