inductive essay meaning

📕 Studying HQ

Inductive essays: tips, examples, and topics, carla johnson.

• June 14, 2023
• Essay Topics and Ideas , How to Guides

Inductive essays are a common type of academic writing. To come to a conclusion, you have to look at the evidence and figure out what it all means. Inductive essays start with a set of observations or evidence and then move toward a conclusion. Deductive essays start with a thesis statement and then give evidence to support it. This type of essay is often used in the social sciences, humanities, and natural sciences.

The goal of an inductive essay is to look at the evidence and draw a conclusion from it. It requires carefully analyzing and interpreting the evidence and being able to draw logical conclusions from it. Instead of starting with a conclusion in mind and trying to prove it, the goal is to use the evidence to build a case for that conclusion.

You can’t say enough about how important it is to look at evidence before coming to a conclusion. In today’s world, where information is easy to find and often contradictory, it is important to be able to sort through the facts to come to a good decision. It is also important to be able to tell when the evidence isn’t complete or doesn’t prove anything, and to be able to admit when there is uncertainty.

In the sections that follow, we’ll talk about some tips for writing good inductive essays, show you some examples of good inductive essays, and give you some ideas for topics for your next inductive essay. By the end of this article, you’ll know more about how to write an inductive essay well.

What You'll Learn

Elements of an Inductive Essay

Most of the time, an inductive essay has three main parts: an intro, body paragraphs, and a conclusion.

The introduction should explain what the topic is about and show the evidence that will be looked at in the essay . It should also have a thesis statement that sums up the conclusion that will be drawn from the evidence.

In the body paragraphs, you should show and explain the evidence. Each paragraph should focus on one piece of evidence and explain how it supports the thesis statement . The analysis should make sense and be well-supported, and there should be a clear link between the evidence and the conclusion.

In the conclusion, you should sum up the evidence and the conclusion you came to based on it. It should also put the conclusion in a bigger picture by explaining why it’s important and what it means for the topic at hand.

How to Choose a Topic for an Inductive Essay

It can be hard to choose a topic for an inductive essay, but there are a few things you can do that will help.

First, it’s important to look at the assignment prompt carefully. What’s the question you’re supposed to answer? What evidence do you have to back up your claim? To choose a topic that is both possible and interesting , you need to understand the prompt and the evidence you have.

Next, brainstorming can be a good way to come up with ideas. Try writing down all the ideas that come to mind when you think about the prompt. At this point, it doesn’t matter if the ideas are good or not. The goal is to come up with as many ideas as possible.

Once you have a list of possible topics , it’s important to pick one that you can handle and that you’re interested in. Think about how big the topic is and if you will have enough time to analyze the evidence in enough depth for the assignment . Also, think about your own passions and interests. If you choose a topic that really interests you, you are more likely to write a good essay .

Some potential topics for an inductive essay include:

– The impact of social media on mental health

– The effectiveness of alternative medicine for treating chronic pain

– The causes of income inequality in the United States

– The relationship between climate change and extreme weather events

– The effects of video game violence on children

By following these tips for choosing a topic and understanding the elements of an inductive essay, you can master the art of this type of academic writing and produce compelling and persuasive essays that draw on evidence to arrive at sound conclusions.

Inductive Essay Outline

An outline can help you to organize your thoughts and ensure that your essay is well-structured. An inductive essay outline typically includes the following sections:

– Introduction: The introduction should provide background information on the topic and present the evidence that will be analyzed in the essay . It should also include a thesis statement that summarizes the conclusion that will be drawn from the evidence.

– Body Paragraphs: The body paragraphs should present the evidence and analyze it in depth. Each paragraph should focus on a specific piece of evidence and explain how it supports the thesis statement . The analysis should be logical and well-supported, with clear connections made between the evidence and the conclusion.

– Conclusion: The conclusion should summarize the evidence and the conclusion that was drawn from it. It should also provide a broader context for the conclusion, explaining why it matters and what implications it has for the topic at hand.

Inductive Essay Structure

The structure of an inductive essay is similar to that of other types of academic essays. It typically includes the following elements:

– Thesis statement: The thesis statement should summarize the conclusion that will be drawn from the evidence and provide a clear focus for the essay .

– Introduction: The introduction should provide background information on the topic and present the evidence that will be analyzed in the essay. It should also include a thesis statement that summarizes the conclusion that will be drawn from the evidence.

– Body Paragraphs: The body paragraphs should present the evidence and analyze it in depth. Each paragraph should focus on a specific piece of evidence and explain how it supports the thesis statement. The analysis should be logical and well-supported, with clear connections made between the evidence and the conclusion.

It is important to note that the body paragraphs can be organized in different ways depending on the nature of the evidence and the argument being made. For example, you may choose to organize the paragraphs by theme or chronologically. Regardless of the organization, each paragraph should be focused and well-supported with evidence.

By following this structure, you can ensure that your inductive essay is well-organized and persuasive, drawing on evidence to arrive at a sound conclusion. Remember to carefully analyze the evidence, and to draw logical connections between the evidence and the conclusion. With practice, you can master the art of inductive essays and become a skilled academic writer.

Inductive Essay Examples

Examples of successful inductive essays can provide a helpful model for your own writing. Here are some examples of inductive essay topics:

– Example 1: The Link Between Smoking and Lung Cancer: This essay could look at the studies and statistics that have been done on the link between smoking and lung cancer and come to a conclusion about how strong it is.

– Example 2: The Effects of Social Media on Mental Health: This essay could look at the studies and personal experiences that have been done on the effects of social media on mental health to come to a conclusion about the effects of social media on mental health.

– Example 3: The Effects of Climate Change on Agriculture: This essay could look at the studies and expert opinions on the effects of climate change on agriculture to come to a conclusion about how it might affect food production..

– Example 4: The Benefits of a Plant-Based Diet: This essay could look at the available evidence about the benefits of a plant-based diet, using studies and dietary guidelines to come to a conclusion about the health benefits of this type of diet.

– Example 5: The Effects of Parenting Styles on Child Development: This essay could look at the studies and personal experiences that have been done on the effects of parenting styles on child development and come to a conclusion about the best way to raise a child.

Tips for Writing an Effective Inductive Essay

Here are some tips for writing acompelling and effective inductive essay:

1. Presenting evidence in a logical and organized way: It is important to present evidence in a clear and organized way that supports the thesis statement and the conclusion. Use topic sentences and transitions to make the connections between the evidence and the conclusion clear for the reader.

2. Considering alternative viewpoints: When analyzing evidence, it is important to consider alternative viewpoints and opinions. Acknowledge counterarguments and address them in your essay, demonstrating why your conclusion is more compelling.

3. Using strong and credible sources: Use credible sources such as peer-reviewed journal articles , statistics, and expert opinions to support your argument. Avoid relying on unreliable sources or anecdotal evidence.

4. Avoiding fallacies and biases: Be aware of logical fallacies and biases that can undermine the credibility of your argument. Avoid making assumptions or jumping to conclusions without sufficient evidence.

By following these tips, you can write an effective inductive essay that draws on evidence to arrive at a sound conclusion. Remember to carefully analyze the evidence, consider alternative viewpoints, and use credible sources to support your argument. With practice and dedication, you can master the art of inductive essays and become a skilled academic writer.

Frequently Asked Questions

1. what is an inductive essay.

An inductive essay is an academic writing that starts with a set of observations or evidence and then works towards a conclusion. The essay requires careful analysis and interpretation of evidence, and the ability to draw logical conclusions based on that evidence.

2. What are the elements of an inductive essay?

An inductive essay typically consists of an introduction, body paragraphs, and a conclusion. The introduction provides background information and presents the thesis statement. The body paragraphs present the evidence and analyze it in depth. The conclusion summarizes the evidence and the conclusion drawn from it.

3. How do I choose a topic for an inductive essay?

To choose a topic for an inductive essay, carefully analyze the assignment prompt, brainstorm ideas, narrow down the topic, and select a topic that interests you.

4. What is the difference between an inductive essay and a deductive essay?

An inductive essay starts with evidence and works towards a conclusion, while a deductive essay starts with a thesis statement and provides arguments to support it.

5. How do I structure an inductive essay?

An inductive essay typically follows a structure that includes a thesis statement, introduction, body paragraphs, and conclusion.

Inductive essays are an important type of academic writing that require careful analysis and interpretation of evidence to come to a conclusion. By using the advice in this article, you can become a good inductive essay writer. Remember to carefully look at the evidence, think about other points of view, use reliable sources, and stay away from logical errors and biases. In conclusion , learning how to write inductive essays is important for developing critical thinking skills and making arguments that are compelling and convincing. You can make a valuable contribution to your field of study and to society as a whole by looking at the facts and coming to logical conclusions. With practice and hard work , you can learn to write good inductive essays that will help you in school and in your career.

Start by filling this short order form order.studyinghq.com

And then follow the progressive flow. 

Having an issue, chat with us here

Cathy, CS. 

New Concept ? Let a subject expert write your paper for You​

Have a subject expert write for you now, have a subject expert finish your paper for you, edit my paper for me, have an expert write your dissertation's chapter, popular topics.

Business StudyingHq Essay Topics and Ideas How to Guides Samples

• Nursing Solutions
• Study Guides
• Free Study Database for Essays
• Privacy Policy
• Writing Service 
• Discounts / Offers 

Study Hub: 

• Studying Blog
• Topic Ideas 
• How to Guides
• Business Studying 
• Nursing Studying 
• Literature and English Studying

Writing Tools  

• Citation Generator
• Topic Generator
• Paraphrasing Tool
• Conclusion Maker
• Research Title Generator
• Thesis Statement Generator
• Summarizing Tool
• Terms and Conditions
• Confidentiality Policy
• Cookies Policy
• Refund and Revision Policy

Our samples and other types of content are meant for research and reference purposes only. We are strongly against plagiarism and academic dishonesty. 

Contact Us:

📧 [email protected]

📞 +15512677917

2012-2024 © studyinghq.com. All rights reserved

• Academic Writing / Online Writing Instruction

Inductive vs. Deductive Writing

by Purdue Global Academic Success Center and Writing Center · Published February 25, 2015 · Updated February 24, 2015

Dr. Tamara Fudge, Kaplan University professor in the School of Business and IT

There are several ways to present information when writing, including those that employ inductive and deductive reasoning . The difference can be stated simply:

• Inductive reasoning presents facts and then wraps them up with a conclusion .
• Deductive reasoning presents a thesis statement and then provides supportive facts or examples.

Which should the writer use? It depends on content, the intended audience , and your overall purpose .

If you want your audience to discover new things with you , then inductive writing might make sense.   Here is n example:

My dog Max wants to chase every non-human living creature he sees, whether it is the cats in the house or rabbits and squirrels in the backyard. Sources indicate that this is a behavior typical of Jack Russell terriers. While Max is a mixed breed dog, he is approximately the same size and has many of the typical markings of a Jack Russell. From these facts along with his behaviors, we surmise that Max is indeed at least part Jack Russell terrier.

Within that short paragraph, you learned about Max’s manners and a little about what he might look like, and then the concluding sentence connected these ideas together. This kind of writing often keeps the reader’s attention, as he or she must read all the pieces of the puzzle before they are connected.

Purposes for this kind of writing include creative writing and perhaps some persuasive essays, although much academic work is done in deductive form.

If your audience is not likely going to read the entire written piece, then deductive reasoning might make more sense, as the reader can look for what he or she wants by quickly scanning first sentences of each paragraph. Here is an example:

My backyard is in dire need of cleaning and new landscaping. The Kentucky bluegrass that was planted there five years ago has been all but replaced by Creeping Charlie, a particularly invasive weed. The stone steps leading to the house are in some disrepair, and there are some slats missing from the fence. Perennials were planted three years ago, but the moles and rabbits destroyed many of the bulbs, so we no longer have flowers in the spring.

The reader knows from the very first sentence that the backyard is a mess! This paragraph could have ended with a clarifying conclusion sentence; while it might be considered redundant to do so, the scientific community tends to work through deductive reasoning by providing (1) a premise or argument – which could also be called a thesis statement, (2) then evidence to support the premise, and (3) finally the conclusion.

Purposes for this kind of writing include business letters and project documents, where the client is more likely to skim the work for generalities or to hunt for only the parts that are important to him or her. Again, scientific writing tends to follow this format as well, and research papers greatly benefit from deductive writing.

Whether one method or another is chosen, there are some other important considerations. First, it is important that the facts/evidence be true. Perform research carefully and from appropriate sources; make sure ideas are cited properly. You might need to avoid absolute words such as “always,” “never,” and “only,” because they exclude any anomalies. Try not to write questions: the writer’s job is to provide answers instead. Lastly, avoid quotes in thesis statements or conclusions, because they are not your own words – and thus undermine your authority as the paper writer.

Share this:

• Click to email a link to a friend (Opens in new window)
• Click to share on Facebook (Opens in new window)
• Click to share on Reddit (Opens in new window)
• Click to share on Twitter (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to print (Opens in new window)

Tags: Critical thinking Reasoning

• Next story  Winter Reading for Online Faculty
• Previous story  Your Students are 13 Minutes Away From Avoiding Plagiarism

You may also like...

Why not finally answer “why”.

April 29, 2015

 by Purdue Global Academic Success Center and Writing Center · Published April 29, 2015 · Last modified April 28, 2015

Brexit Voters Broke It and Now Regret It-Part I: Establishing the Importance of Teaching and Learning in Developing an Educated, Global Electorate

October 26, 2016

 by Purdue Global Academic Success Center and Writing Center · Published October 26, 2016 · Last modified April 8, 2020

The Big Misconception about Writing to Learn

June 10, 2015

 by Purdue Global Academic Success Center and Writing Center · Published June 10, 2015

7 Responses

• Pingbacks 2

Helpful Thanks

Great article! This was helpful and provided great information.

Very helpful

very helpful . thank you

Very helpful.

[…] + Read More Here […]

[…] begin with alarming statistics and the urgency of action. However, articles often transition into inductive storytelling by featuring firsthand accounts of climate-related events or interviews with affected communities. […]

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Notify me of follow-up comments by email.

Notify me of new posts by email.

Inductive VS Deductive Reasoning – The Meaning of Induction and Deduction, with Argument Examples

If you're conducting research on a topic, you'll use various strategies and methods to gather information and come to a conclusion.

Two of those methods are inductive and deductive reasoning.

So what's the difference between inductive and deductive reasoning, when should you use each method, and is one better than the other?

We'll answer those questions and give you some examples of both types of reasoning in this article.

What is Inductive Reasoning?

The method behind inductive reasoning.

When you're using inductive reasoning to conduct research, you're basing your conclusions off your observations. You gather information - from talking to people, reading old newspapers, observing people, animals, or objects in their natural habitat, and so on.

Inductive reasoning helps you take these observations and form them into a theory. So you're starting with some more specific information (what you've seen/heard) and you're using it to form a more general theory about the way things are.

What does the inductive reasoning process look like?

You can think of this process as a reverse funnel – starting with more specifics and getting broader as you reach your conclusions (theory).

Some people like to think of it as a "bottom up" approach (meaning you're starting at the bottom with the info and are going up to the top where the theory forms).

Here's an example of an inductive argument:

Observation (premise): My Welsh Corgis were incredibly stubborn and independent (specific observation of behavior). Observation (premise): My neighbor's Corgis are the same way (another specific observation of behavior). Theory: All Welsh Corgis are incredibly stubborn and independent (general statement about the behavior of Corgis).

As you can see, I'm basing my theory on my observations of the behavior of a number of Corgis. Since I only have a small amount of data, my conclusion or theory will be quite weak.

If I was able to observe the behavior of 1000 Corgis (omg that would be amazing), my conclusion would be stronger – but still not certain. Because what if 10 of them were extremely well-behaved and obedient? Or what if the 1001st Corgi was?

So, as you can see, I can make a general statement about Corgis being stubborn, but I can't say that ALL of them are.

What can you conclude with inductive reasoning?

As I just discussed, one of the main things to know about inductive reasoning is that any conclusions you make from inductive research will not be 100% certain or confirmed.

Let's talk about the language we use to describe inductive arguments and conclusions. You can have a strong argument (if your premise(s) are true, meaning your conclusion is probably true). And that argument becomes cogent if the conclusion ends up being true.

Still, even if the premises of your argument are true, and that means that your conclusion is probably true, or likely true, or true much of the time – it's not certain.

And – weirdly enough – your conclusion can still be false even if all your premises are true (my Corgis were stubborn, my neighbor's corgis were stubborn, perhaps a friend's Corgis and the Queen of England's Corgis were stubborn...but that doesn't guarantee that all Corgis are stubborn).

How to make your inductive arguments stronger

If you want to make sure your inductive arguments are as strong as possible, there are a couple things you can do.

First of all, make sure you have a large data set to work with. The larger your sample size, the stronger (and more certain/conclusive) your results will be. Again, thousands of Corgis are better than four (I mean, always, amiright?).

Second, make sure you're taking a random and representative sample of the population you're studying. So, for example, don't just study Corgi puppies (cute as they may be). Or show Corgis (theoretically they're better trained). You'd want to make sure you looked at Corgis from all walks of life and of all ages.

If you want to dig deeper into inductive reasoning, look into the three different types – generalization, analogy, and causal inference. You can also look into the two main methods of inductive reasoning, enumerative and eliminative. But those things are a bit out of the scope of this beginner's guide. :)

What is Deductive Reasoning?

The method behind deductive reasoning.

In order to use deductive reasoning, you have to have a theory to begin with. So inductive reasoning usually comes before deductive in your research process.

Once you have a theory, you'll want to test it to see if it's valid and your conclusions are sound. You do this by performing experiments and testing your theory, narrowing down your ideas as the results come in. You perform these tests until only valid conclusions remain.

What does the deductive reasoning process look like?

You can think of this as a proper funnel – you start with the broad open top end of the funnel and get more specific and narrower as you conduct your deductive research.

Some people like to think of this as a "top down" approach (meaning you're starting at the top with your theory, and are working your way down to the bottom/specifics). I think it helps to think of this as " reductive " reasoning – you're reducing your theories and hypotheses down into certain conclusions.

Here's an example of a deductive argument:

We'll use a classic example of deductive reasoning here – because I used to study Greek Archaeology, history, and language:

Theory: All men are mortal Premise: Socrates is a man Conclusion: Therefore, Socrates is mortal

As you can see here, we start off with a general theory – that all men are mortal. (This is assuming you don't believe in elves, fairies, and other beings...)

Then we make an observation (develop a premise) about a particular example of our data set (Socrates). That is, we say that he is a man, which we can establish as a fact.

Finally, because Socrates is a man, and based on our theory, we conclude that Socrates is therefore mortal (since all men are mortal, and he's a man).

You'll notice that deductive reasoning relies less on information that could be biased or uncertain. It uses facts to prove the theory you're trying to prove. If any of your facts lead to false premises, then the conclusion is invalid. And you start the process over.

What can you conclude with deductive reasoning?

Deductive reasoning gives you a certain and conclusive answer to your original question or theory. A deductive argument is only valid if the premises are true. And the arguments are sound when the conclusion, following those valid arguments, is true.

To me, this sounds a bit more like the scientific method. You have a theory, test that theory, and then confirm it with conclusive/valid results.

To boil it all down, in deductive reasoning:

"If all premises are true, the terms are clear , and the rules of deductive logic are followed, then the conclusion reached is necessarily true ." ( Source )

So Does Sherlock Holmes Use Inductive or Deductive Reasoning?

Sherlock Holmes is famous for using his deductive reasoning to solve crimes. But really, he mostly uses inductive reasoning. Now that we've gone through what inductive and deductive reasoning are, we can see why this is the case.

Let's say Sherlock Holmes is called in to work a case where a woman was found dead in her bed, under the covers, and appeared to be sleeping peacefully. There are no footprints in the carpet, no obvious forced entry, and no immediately apparent signs of struggle, injury, and so on.

Sherlock observes all this as he looks in, and then enters the room. He walks around the crime scene making observations and taking notes. He might talk to anyone who lives with her, her neighbors, or others who might have information that could help him out.

Then, once he has all the info he needs, he'll come to a conclusion about how the woman died.

That pretty clearly sounds like an inductive reasoning process to me.

Now you might say - what if Sherlock found the "smoking gun" so to speak? Perhaps this makes his arguments and process seem more deductive.

But still, remember how he gets to his conclusions: starting with observations and evidence, processing that evidence to come up with a hypothesis, and then forming a theory (however strong/true-seeming) about what happened.

How to Use Inductive and Deductive Reasoning Together

As you might be able to tell, researchers rarely just use one of these methods in isolation. So it's not that deductive reasoning is better than inductive reasoning, or vice versa – they work best when used in tandem.

Often times, research will begin inductively. The researcher will make their observations, take notes, and come up with a theory that they want to test.

Then, they'll come up with ways to definitively test that theory. They'll perform their tests, sort through the results, and deductively come to a sure conclusion.

So if you ever hear someone say "I deduce that x happened", they better make sure they're working from facts and not just observations. :)

TL;DR: Inductive vs Deductive Reasoning – What are the Main Differences?

Inductive reasoning:.

• Based on observations, conversations, stuff you've read
• Starts with information/evidence and works towards a broader theory
• Arguments can be strong and cogent, but never valid or sound (that is, certain)
• Premises can all be true, but conclusion doesn't have to be true

Deductive reasoning:

• Based on testing a theory, narrowing down the results, and ending with a conclusion
• Starts with a broader theory and works towards certain conclusion
• Arguments can be valid/invalid or sound/unsound, because they're based on facts
• If premises are true, conclusion has to be true

And here's a cool and helpful chart if you're a visual learner:

That's about it!

Now, if you need to conduct some research, you should have a better idea of where to start – and where to go from there.

Just remember that induction is all about observing, hypothesizing, and forming a theory. Deducing is all about taking that (or any) theory, boiling it down, and testing until a certain conclusion(s) is all that remains.

Happy reasoning!

Former archaeologist, current editor and podcaster, life-long world traveler and learner.

If you read this far, thank the author to show them you care. Say Thanks

Learn to code for free. freeCodeCamp's open source curriculum has helped more than 40,000 people get jobs as developers. Get started

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5: Inductive Arguments

• Last updated
• Save as PDF
• Page ID 29607

• Golden West College via NGE Far Press

Unlike deductive arguments, inductive reasoning allows for the possibility that the conclusion is false, even if all of the premises are true. Instead of being valid or invalid, inductive arguments are either strong or weak , which describes how probable it is that the conclusion is true. Another crucial difference is that deductive certainty is impossible in non-axiomatic systems, such as reality, leaving inductive reasoning as the primary route to (probabilistic) knowledge of such systems.

• 5.1: Prelude to Inductive Arguments
• 5.2: Cogency and Strong Arguments Inductive arguments are said to be either strong or weak. There’s no absolute cut-off between strength and weakness, but some arguments will be very strong and others very weak, so the distinction is still useful even if it is not precise. A strong argument is one where, if the premises were true, the conclusion would be very likely to be true. A weak argument is one where the conclusion does not follow from the premises.
• 5.3: Causality and Scientific Reasoning
• 5.4: Analogy
• 5.5: Statistical Reasoning- Bayes’ Theorem Bayesian reasoning is about how to revise our beliefs in the light of evidence. We'll start by considering one scenario in which the strength of the evidence has clear numbers attached.
• 5.6: Legal Reasoning and Moral Reasoning In this discussion of moral reasoning, we will learn how to decide what to do. In this sense, moral reasoning is the most practical part of the process. When we reason about morality we build arguments, just like when we reason about anything else. But arguments involving moral propositions have to be constructed in a special way. This is partly to help us avoid the Naturalistic Fallacy. But it is also to help ensure that our arguments about morality are consistent.
• 5.7: Editing Your Final Essay

Inductive and Deductive Assignment (McMahon)

The next writing assignment we will be concentrating on will be the construction of persuasive passages using induction, deduction, and expressive language or analogy. These passages should be used to further strengthen and develop your Pro/Con and/or your Rogerian essays.

1. Inductive reasoning is the process of reasoning from specifics to the general. We draw general conclusions based on discrete, specific everyday experiences. Because both writers and readers share this reasoning process, induction can be a highly effective strategy for persuasion. A truly persuasive and effective inductive argument proceeds through an accumulation of many specifics. Within your own essays you should use support from outside sources, personal experience, and specific examples to fully develop your inductive passages. Also, keep in mind that conclusions drawn from inductive reasoning are always only probable. To use induction effectively, a writer must demonstrate that the specifics are compelling and thus justify the conclusion but never claim that the conclusion is guaranteed in all situations. In addition, a writer must keep in mind who his/her audience is and what specifics or evidence will persuade the audience to accept the conclusion. Finally, a writer who is reasoning inductively must be cautious of hasty generalizations in which the specifics are inadequate to justify the conclusions.

2. Deductive reasoning is the process of reasoning from general statements agreed to be true to a certain and logical conclusion. Again, like inductive reasoning, deductive reasoning is a familiar strategy we use in our everyday lives and is a potentially effective persuasive strategy. However, unlike inductive reasoning when the conclusion may be justified but is always only probable, the conclusion reached deductively must be logically certain. Most deductive arguments begin with a general statement that has already been "proven" inductively and is now accepted by most people as true. Today, most deductive general statements involve commonly held values or established scientific fact. A writer who uses deduction to frame an argument must be absolutely certain that the general statement is accepted as true and then must demonstrate the relationship between this general statement and the specific claim, thus proving beyond a doubt the conclusion. An effective deductive argument is one in which your audience accepts the general statement and is then logically compelled by the development of the argument to accept your conclusion.

3. An analogy helps a writer further develop and support an idea he/she is trying to convey to a reader. In an analogy a comparison is drawn between the principle idea and something else a reader is familiar with. Thus, the comparison clarifies the principle idea. Analogies within persuasive writing appeal to either a reader's value system or to a reader's reason and logic. Asking a reader to consider an idea, issue, or problem in the context of something else can both clarify the idea and persuade the reader to accept our interpretation of the idea. Please note: analogies only work when the subjects you are comparing have some similarities. If the things you compare are too dissimilar, your readers will dismiss the analogy and fail to be persuaded of your idea.

• Inductive and Deductive Reasoning

Two Ways of Understanding

We have two basic approaches for how we come to believe something is true.

The first way is that we are exposed to several different examples of a situation, and from those examples, we conclude a general truth. For instance, you visit your local grocery store daily to pick up necessary items. You notice that on Friday, two weeks ago, all the clerks in the store were wearing football jerseys. Again, last Friday, the clerks wore their football jerseys. Today, also a Friday, they’re wearing them again. From just these observations, you can conclude that on all Fridays, these supermarket employees will wear football jerseys to support their local team.

This type of pattern recognition, leading to a conclusion, is known as inductive reasoning .

Knowledge can also move the opposite direction. Say that you read in the news about a tradition in a local grocery store, where employees wore football jerseys on Fridays to support the home team. This time, you’re starting from the overall rule, and you would expect individual evidence to support this rule. Each time you visited the store on a Friday, you would expect the employees to wear jerseys.

Such a case, of starting with the overall statement and then identifying examples that support it, is known as deductive reasoning .

The Power of Inductive Reasoning

You have been employing  inductive reasoning  for a very long time. Inductive reasoning is based on your ability to recognize meaningful patterns and connections. By taking into account both examples and your understanding of how the world works, induction allows you to conclude that something is likely to be true. By using induction, you move from specific data to a generalization that tries to capture what the data “mean.”

Imagine that you ate a dish of strawberries and soon afterward your lips swelled. Now imagine that a few weeks later you ate strawberries and soon afterwards your lips again became swollen. The following month, you ate yet another dish of strawberries, and you had the same reaction as formerly. You are aware that swollen lips can be a sign of an allergy to strawberries. Using induction, you conclude that, more likely than not, you are allergic to strawberries.

Data : After I ate strawberries, my lips swelled (1st time).

Data : After I ate strawberries, my lips swelled (2nd time).

Data : After I ate strawberries, my lips swelled (3rd time).

Additional Information : Swollen lips after eating strawberries may be a sign of an allergy.

Conclusion : Likely I am allergic to strawberries.

The results of inductive thinking can be skewed if relevant data are overlooked. In the previous example, inductive reasoning was used to conclude that I am likely allergic to strawberries after suffering multiple instances of my lips swelling. Would I be as confident in my conclusion if I were eating strawberry shortcake on each of those occasions? Is it reasonable to assume that the allergic reaction might be due to another ingredient besides strawberries?

This example illustrates that inductive reasoning must be used with care. When evaluating an inductive argument, consider

• the amount of the data,
• the quality of the data,
• the existence of additional data,
• the relevance of necessary additional information, and
• the existence of additional possible explanations.

Inductive Reasoning Put to Work

A synopsis of the features, benefits, and drawbacks of inductive reasoning can be found in this video.

The Power of Deductive Reasoning

Deductive reasoning is built on two statements whose logical relationship should lead to a third statement that is an unquestionably correct conclusion, as in the following example.

All raccoons are omnivores. This animal is a raccoon. This animal is an omnivore.

If the first statement is true (All raccoons are omnivores) and the second statement is true (This animal is a raccoon), then the conclusion (This animal is an omnivore) is unavoidable. If a group must have a certain quality, and an individual is a member of that group, then the individual must have that quality.

Going back to the example from the opening of this page, we could frame it this way:

Grocery store employees wear football jerseys on Fridays. Today is Friday. Grocery store employees will be wearing football jerseys today.

Unlike inductive reasoning, deductive reasoning allows for certainty as long as certain rules are followed.

Evaluating the Truth of a Premise

A formal argument may be set up so that, on its face, it looks logical. However, no matter how well-constructed the argument is, the additional information required must be true. Otherwise any inferences based on that additional information will be invalid. 

Inductive reasoning can often be hidden inside a deductive argument. That is, a generalization reached through inductive reasoning can be turned around and used as a starting “truth” a deductive argument. For instance, 

Most Labrador retrievers are friendly. Kimber is a Labrador retriever. Therefore, Kimber is friendly.

In this case we cannot know for certain that Kimber is a friendly Labrador retriever. The structure of the argument may look logical, but it is based on observations and generalizations rather than indisputable facts.

Methods to Evaluate the Truth of a Premise

One way to test the accuracy of a premise is to apply the same questions asked of inductive arguments. As a recap, you should consider

• the relevance of the additional data, and
• the existence of additional possible explanations.

Determine whether the starting claim is based upon a sample that is both representative and sufficiently large, and ask yourself whether all relevant factors have been taken into account in the analysis of data that leads to a generalization.

Another way to evaluate a premise is to determine whether its source is credible.

• Are the authors identified?
• What is their background?
• Was the claim something you found on an undocumented website?
• Did you find it in a popular publication or a scholarly one?
• How complete, how recent, and how relevant were the studies or statistics discussed in the source?

Overview and Recap

A synopsis of the features, benefits, and drawbacks of deductive reasoning can be found in this video.

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Inductive Reasoning. Authored by : Chuck Creager Jr.. Located at : https://youtu.be/wzEOwleZNnA . License : CC BY: Attribution
• Deductive Reasoning. Authored by : Chuck Creager Jr.. Located at : https://youtu.be/oBnKgxcdSyM . License : All Rights Reserved . License Terms : Standard YouTube License
• The Logical Structure of Arguments. Provided by : Radford University. Located at : http://lcubbison.pressbooks.com/chapter/core-201-analyzing-arguments/ . Project : Core Curriculum Handbook. License : Public Domain: No Known Copyright
• Table of Contents

Instructor Resources (available upon sign-in)

• Overview of Instructor Resources
• Quiz Survey

Reading: Types of Reading Material

• Introduction to Reading
• Outcome: Types of Reading Material
• Characteristics of Texts, Part 1
• Characteristics of Texts, Part 2
• Characteristics of Texts, Part 3
• Characteristics of Texts, Conclusion
• Self Check: Types of Writing

Reading: Reading Strategies

• Outcome: Reading Strategies
• The Rhetorical Situation
• Academic Reading Strategies
• Self Check: Reading Strategies

Reading: Specialized Reading Strategies

• Outcome: Specialized Reading Strategies
• Online Reading Comprehension
• How to Read Effectively in Math
• How to Read Effectively in the Social Sciences
• How to Read Effectively in the Sciences
• 5 Step Approach for Reading Charts and Graphs
• Self Check: Specialized Reading Strategies

Reading: Vocabulary

• Outcome: Vocabulary
• Strategies to Improve Your Vocabulary
• Using Context Clues
• The Relationship Between Reading and Vocabulary
• Self Check: Vocabulary

Reading: Thesis

• Outcome: Thesis
• Locating and Evaluating Thesis Statements
• The Organizational Statement
• Self Check: Thesis

Reading: Supporting Claims

• Outcome: Supporting Claims
• Types of Support
• Supporting Claims
• Self Check: Supporting Claims

Reading: Logic and Structure

• Outcome: Logic and Structure
• Rhetorical Modes
• Diagramming and Evaluating Arguments
• Logical Fallacies
• Evaluating Appeals to Ethos, Logos, and Pathos
• Self Check: Logic and Structure

Reading: Summary Skills

• Outcome: Summary Skills
• How to Annotate
• Paraphrasing
• Quote Bombs
• Summary Writing
• Self Check: Summary Skills
• Conclusion to Reading

Writing Process: Topic Selection

• Introduction to Writing Process
• Outcome: Topic Selection
• Starting a Paper
• Choosing and Developing Topics
• Back to the Future of Topics
• Developing Your Topic
• Self Check: Topic Selection

Writing Process: Prewriting

• Outcome: Prewriting
• Prewriting Strategies for Diverse Learners
• Rhetorical Context
• Working Thesis Statements
• Self Check: Prewriting

Writing Process: Finding Evidence

• Outcome: Finding Evidence
• Using Personal Examples
• Performing Background Research
• Listening to Sources, Talking to Sources
• Self Check: Finding Evidence

Writing Process: Organizing

• Outcome: Organizing
• Moving Beyond the Five-Paragraph Theme
• Introduction to Argument
• The Three-Story Thesis
• Organically Structured Arguments
• Logic and Structure
• The Perfect Paragraph
• Introductions and Conclusions
• Self Check: Organizing

Writing Process: Drafting

• Outcome: Drafting
• From Outlining to Drafting
• Flash Drafts
• Self Check: Drafting

Writing Process: Revising

• Outcome: Revising
• Seeking Input from Others
• Responding to Input from Others
• The Art of Re-Seeing
• Higher Order Concerns
• Self Check: Revising

Writing Process: Proofreading

• Outcome: Proofreading
• Lower Order Concerns
• Proofreading Advice
• "Correctness" in Writing
• The Importance of Spelling
• Punctuation Concerns
• Self Check: Proofreading
• Conclusion to Writing Process

Research Process: Finding Sources

• Introduction to Research Process
• Outcome: Finding Sources
• The Research Process
• Finding Sources
• What are Scholarly Articles?
• Finding Scholarly Articles and Using Databases
• Database Searching
• Advanced Search Strategies
• Preliminary Research Strategies
• Reading and Using Scholarly Sources
• Self Check: Finding Sources

Research Process: Source Analysis

• Outcome: Source Analysis
• Evaluating Sources
• CRAAP Analysis
• Evaluating Websites
• Synthesizing Sources
• Self Check: Source Analysis

Research Process: Writing Ethically

• Outcome: Writing Ethically
• Academic Integrity
• Defining Plagiarism
• Avoiding Plagiarism
• Using Sources in Your Writing
• Self Check: Writing Ethically

Research Process: MLA Documentation

• Introduction to MLA Documentation
• Outcome: MLA Documentation
• MLA Document Formatting
• MLA Works Cited
• Creating MLA Citations
• MLA In-Text Citations
• Self Check: MLA Documentation
• Conclusion to Research Process

Grammar: Nouns and Pronouns

• Introduction to Grammar
• Outcome: Nouns and Pronouns
• Pronoun Cases and Types
• Pronoun Antecedents
• Try It: Nouns and Pronouns
• Self Check: Nouns and Pronouns

Grammar: Verbs

• Outcome: Verbs
• Verb Tenses and Agreement
• Non-Finite Verbs
• Complex Verb Tenses
• Try It: Verbs
• Self Check: Verbs

Grammar: Other Parts of Speech

• Outcome: Other Parts of Speech
• Comparing Adjectives and Adverbs
• Adjectives and Adverbs
• Conjunctions
• Prepositions
• Try It: Other Parts of Speech
• Self Check: Other Parts of Speech

Grammar: Punctuation

• Outcome: Punctuation
• End Punctuation
• Hyphens and Dashes
• Apostrophes and Quotation Marks
• Brackets, Parentheses, and Ellipses
• Semicolons and Colons
• Try It: Punctuation
• Self Check: Punctuation

Grammar: Sentence Structure

• Outcome: Sentence Structure
• Parts of a Sentence
• Common Sentence Structures
• Run-on Sentences
• Sentence Fragments
• Parallel Structure
• Try It: Sentence Structure
• Self Check: Sentence Structure

Grammar: Voice

• Outcome: Voice
• Active and Passive Voice
• Using the Passive Voice
• Conclusion to Grammar
• Try It: Voice
• Self Check: Voice

Success Skills

• Introduction to Success Skills
• Habits for Success
• Critical Thinking
• Time Management
• Writing in College
• Computer-Based Writing
• Conclusion to Success Skills

“Inductive” vs. “Deductive”: How To Reason Out Their Differences

• What Does Inductive Mean?
• What Does Deductive Mean?
• Inductive Reasoning Vs. Deductive Reasoning

Inductive and deductive are commonly used in the context of logic, reasoning, and science. Scientists use both inductive and deductive reasoning as part of the scientific method . Fictional detectives like Sherlock Holmes are famously associated with methods of deduction (though that’s often not what Holmes actually uses—more on that later). Some writing courses involve inductive and deductive essays.

But what’s the difference between inductive and deductive ? Broadly speaking, the difference involves whether the reasoning moves from the general to the specific or from the specific to the general. In this article, we’ll define each word in simple terms, provide several examples, and even quiz you on whether you can spot the difference.

⚡ Quick summary

Inductive reasoning (also called induction ) involves forming general theories from specific observations. Observing something happen repeatedly and concluding that it will happen again in the same way is an example of inductive reasoning. Deductive reasoning (also called deduction ) involves forming specific conclusions from general premises, as in: everyone in this class is an English major; Jesse is in this class; therefore, Jesse is an English major.

What does inductive mean?

Inductive is used to describe reasoning that involves using specific observations, such as observed patterns, to make a general conclusion. This method is sometimes called induction . Induction starts with a set of premises , based mainly on experience or experimental evidence. It uses those premises to generalize a conclusion .

For example, let’s say you go to a cafe every day for a month, and every day, the same person comes at exactly 11 am and orders a cappuccino. The specific observation is that this person has come to the cafe at the same time and ordered the same thing every day during the period observed. A general conclusion drawn from these premises could be that this person always comes to the cafe at the same time and orders the same thing.

While inductive reasoning can be useful, it’s prone to being flawed. That’s because conclusions drawn using induction go beyond the information contained in the premises. An inductive argument may be highly probable , but even if all the observations are accurate, it can lead to incorrect conclusions.

Follow up this discussion with a look at concurrent vs. consecutive .

In our basic example, there are a number of reasons why it may not be true that the person always comes at the same time and orders the same thing.

Additional observations of the same event happening in the same way increase the probability that the event will happen again in the same way, but you can never be completely certain that it will always continue to happen in the same way.

That’s why a theory reached via inductive reasoning should always be tested to see if it is correct or makes sense.

What else does inductive mean?

Inductive can also be used as a synonym for introductory . It’s also used in a more specific way to describe the scientific processes of electromagnetic and electrostatic induction —or things that function based on them.

What does deductive mean?

Deductive reasoning (also called deduction ) involves starting from a set of general premises and then drawing a specific conclusion that contains no more information than the premises themselves. Deductive reasoning is sometimes called deduction (note that deduction has other meanings in the contexts of mathematics and accounting).

Here’s an example of deductive reasoning: chickens are birds; all birds lay eggs; therefore, chickens lay eggs. Another way to think of it: if something is true of a general class (birds), then it is true of the members of the class (chickens).

Deductive reasoning can go wrong, of course, when you start with incorrect premises. For example, look where this first incorrect statement leads us: all animals that lay eggs are birds; snakes lay eggs; therefore, snakes are birds.

The scientific method can be described as deductive . You first formulate a hypothesis —an educated guess based on general premises (sometimes formed by inductive methods). Then you test the hypothesis with an experiment . Based on the results of the experiment, you can make a specific conclusion as to the accuracy of your hypothesis.

You may have deduced there are related terms to this topic. Start with a look at interpolation vs. extrapolation .

Deductive reasoning is popularly associated with detectives and solving mysteries. Most famously, Sherlock Holmes claimed to be among the world’s foremost practitioners of deduction , using it to solve how crimes had been committed (or impress people by guessing where they had been earlier in the day).

However, despite this association, reasoning that’s referred to as deduction in many stories is actually more like induction or a form of reasoning known as abduction , in which probable but uncertain conclusions are drawn based on known information.

Sherlock’s (and Arthur Conan Doyle ’s) use of the word deduction can instead be interpreted as a way (albeit imprecise) of referring to systematic reasoning in general.

What is the difference between inductive vs. deductive reasoning?

Inductive reasoning involves starting from specific premises and forming a general conclusion, while deductive reasoning involves using general premises to form a specific conclusion.

Conclusions reached via deductive reasoning cannot be incorrect if the premises are true. That’s because the conclusion doesn’t contain information that’s not in the premises. Unlike deductive reasoning, though, a conclusion reached via inductive reasoning goes beyond the information contained within the premises—it’s a generalization , and generalizations aren’t always accurate.

The best way to understand the difference between inductive and deductive reasoning is probably through examples.

Go Behind The Words!

• By clicking "Sign Up", you are accepting Dictionary.com Terms & Conditions and Privacy policies.
• Email This field is for validation purposes and should be left unchanged.

Examples of inductive and deductive reasoning

Examples of inductive reasoning.

Premise: All known fish species in this genus have yellow fins. Conclusion: Any newly discovered species in the genus is likely to have yellow fins.

Premises: This volcano has erupted about every 500 years for the last 1 million years. It last erupted 499 years ago. Conclusion: It will erupt again soon.

Examples of deductive reasoning

Premises: All plants with rainbow berries are poisonous. This plant has rainbow berries. Conclusion: This plant is poisonous.

Premises: I am lactose intolerant. Lactose intolerant people get sick when they consume dairy. This milkshake contains dairy. Conclusion: I will get sick if I drink this milkshake.

Reason your way to the best score by taking our quiz on "inductive" vs. "deductive" reasoning!

Current Events

Science & Technology

Trending Words

[ sted -fast ]

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, automatically generate references for free.

• Knowledge Base
• Methodology

Inductive Reasoning | Types, Examples, Explanation

Published on 4 May 2022 by Pritha Bhandari . Revised on 5 December 2022.

Inductive reasoning is a method of drawing conclusions by going from the specific to the general. It’s usually contrasted with deductive reasoning , where you go from general information to specific conclusions.

Inductive reasoning is also called inductive logic or bottom-up reasoning.

Note: Inductive reasoning is often confused with deductive reasoning. However, in deductive reasoning, you make inferences by going from general premises to specific conclusions.

Table of contents

What is inductive reasoning, inductive reasoning in research, types of inductive reasoning, inductive generalisation, statistical generalisation, causal reasoning, sign reasoning, analogical reasoning, inductive vs deductive reasoning, frequently asked questions about inductive reasoning.

Inductive reasoning is a logical approach to making inferences, or conclusions. People often use inductive reasoning informally in everyday situations.

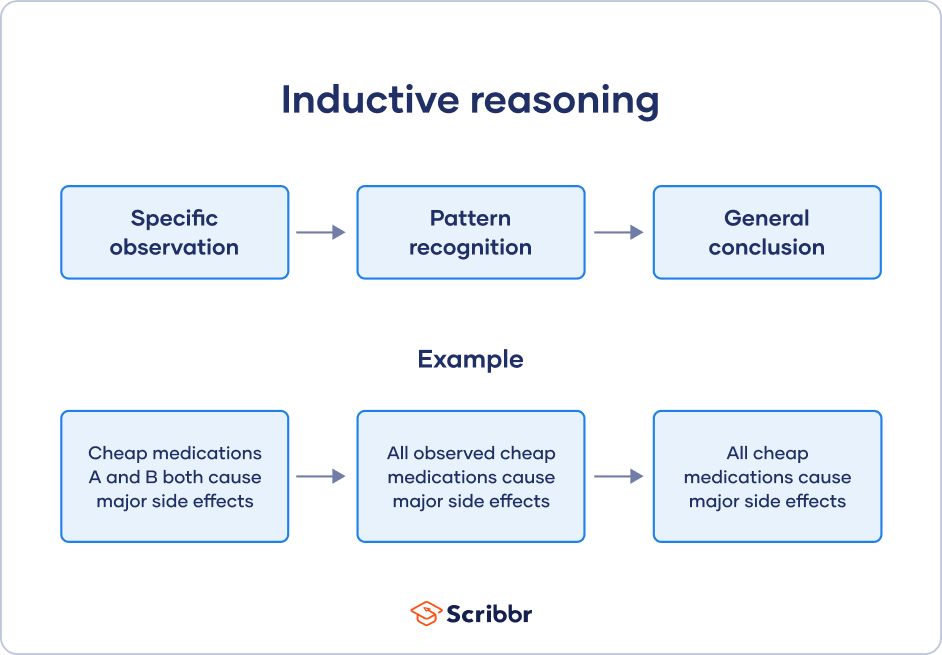
You may have come across inductive logic examples that come in a set of three statements. These start with one specific observation, add a general pattern, and end with a conclusion.

Prevent plagiarism, run a free check.

In inductive research, you start by making observations or gathering data. Then, you take a broad view of your data and search for patterns. Finally, you make general conclusions that you might incorporate into theories.

You distribute a survey to pet owners. You ask about the type of animal they have and any behavioural changes they’ve noticed in their pets since they started working from home. These data make up your observations.

To analyse your data, you create a procedure to categorise the survey responses so you can pick up on repeated themes. You notice a pattern : most pets became more needy and clingy or agitated and aggressive.

Inductive reasoning is commonly linked to qualitative research , but both quantitative and qualitative research use a mix of different types of reasoning.

There are many different types of inductive reasoning that people use formally or informally, so we’ll cover just a few in this article:

Inductive reasoning generalisations can vary from weak to strong, depending on the number and quality of observations and arguments used.

Inductive generalisations use observations about a sample to come to a conclusion about the population it came from.

Inductive generalisations are also called induction by enumeration.

• The flamingos here are all pink.
• All flamingos I’ve ever seen are pink.
• All flamingos must be pink.

Inductive generalisations are evaluated using several criteria:

• Large sample: Your sample should be large for a solid set of observations.
• Random sampling : Probability sampling methods let you generalise your findings.
• Variety: Your observations should be externally valid .
• Counterevidence: Any observations that refute yours falsify your generalisation.

Statistical generalisations use specific numbers to make statements about populations, while non-statistical generalisations aren’t as specific.

These generalisations are a subtype of inductive generalisations, and they’re also called statistical syllogisms.

Here’s an example of a statistical generalisation contrasted with a non-statistical generalisation.

Causal reasoning means making cause-and-effect links between different things.

A causal reasoning statement often follows a standard setup:

• You start with a premise about a correlation (two events that co-occur).
• You put forward the specific direction of causality or refute any other direction.
• You conclude with a causal statement about the relationship between two things.
• All of my white clothes turn pink when I put a red cloth in the washing machine with them.
• My white clothes don’t turn pink when I wash them on their own.
• Putting colourful clothes with light colours causes the colours to run and stain the light-coloured clothes.

Good causal inferences meet a couple of criteria:

• Direction: The direction of causality should be clear and unambiguous based on your observations.
• Strength: There’s ideally a strong relationship between the cause and the effect.

Sign reasoning involves making correlational connections between different things.

Using inductive reasoning, you infer a purely correlational relationship where nothing causes the other thing to occur. Instead, one event may act as a ‘sign’ that another event will occur or is currently occurring.

• Every time Punxsutawney Phil casts a shadow on Groundhog Day, winter lasts six more weeks.
• Punxsutawney Phil doesn’t cause winter to be extended six more weeks.
• His shadow is a sign that we’ll have six more weeks of wintery weather.

It’s best to be careful when making correlational links between variables . Build your argument on strong evidence, and eliminate any confounding variables , or you may be on shaky ground.

Analogical reasoning means drawing conclusions about something based on its similarities to another thing. You first link two things together and then conclude that some attribute of one thing must also hold true for the other thing.

Analogical reasoning can be literal (closely similar) or figurative (abstract), but you’ll have a much stronger case when you use a literal comparison.

Analogical reasoning is also called comparison reasoning.

• Humans and laboratory rats are extremely similar biologically, sharing over 90% of their DNA.
• Lab rats show promising results when treated with a new drug for managing Parkinson’s disease.
• Therefore, humans will also show promising results when treated with the drug.

Inductive reasoning is a bottom-up approach, while deductive reasoning is top-down.

In deductive reasoning, you make inferences by going from general premises to specific conclusions. You start with a theory, and you might develop a hypothesis that you test empirically. You collect data from many observations and use a statistical test to come to a conclusion about your hypothesis.

Inductive research is usually exploratory in nature, because your generalisations help you develop theories. In contrast, deductive research is generally confirmatory.

Sometimes, both inductive and deductive approaches are combined within a single research study.

Inductive reasoning approach

You begin by using qualitative methods to explore the research topic, taking an inductive reasoning approach. You collect observations by interviewing workers on the subject and analyse the data to spot any patterns. Then, you develop a theory to test in a follow-up study.

Deductive reasoning approach

Inductive reasoning is a method of drawing conclusions by going from the specific to the general. It’s usually contrasted with deductive reasoning, where you proceed from general information to specific conclusions.

There are many different types of inductive reasoning that people use formally or informally.

Here are a few common types:

• Inductive generalisation : You use observations about a sample to come to a conclusion about the population it came from.
• Statistical generalisation: You use specific numbers about samples to make statements about populations.
• Causal reasoning: You make cause-and-effect links between different things.
• Sign reasoning: You make a conclusion about a correlational relationship between different things.
• Analogical reasoning: You make a conclusion about something based on its similarities to something else.

In inductive research , you start by making observations or gathering data. Then, you take a broad scan of your data and search for patterns. Finally, you make general conclusions that you might incorporate into theories.

Inductive reasoning takes you from the specific to the general, while in deductive reasoning, you make inferences by going from general premises to specific conclusions.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Bhandari, P. (2022, December 05). Inductive Reasoning | Types, Examples, Explanation. Scribbr. Retrieved 15 April 2024, from https://www.scribbr.co.uk/research-methods/inductive-reasoning-types/

Is this article helpful?

Pritha Bhandari

Other students also liked, what is deductive reasoning | explanation & examples, inductive vs deductive research approach (with examples), a quick guide to experimental design | 5 steps & examples.

• Table of Contents
• Random Entry
• Chronological
• Editorial Information
• About the SEP
• Editorial Board
• How to Cite the SEP
• Special Characters
• Advanced Tools
• Support the SEP
• PDFs for SEP Friends
• Make a Donation
• SEPIA for Libraries
• Entry Contents

Bibliography

Academic tools.

• Friends PDF Preview
• Author and Citation Info
• Back to Top

Inductive Logic

An inductive logic is a logic of evidential support. In a deductive logic, the premises of a valid deductive argument logically entail the conclusion, where logical entailment means that every logically possible state of affairs that makes the premises true must make the conclusion true as well. Thus, the premises of a valid deductive argument provide total support for the conclusion. An inductive logic extends this idea to weaker arguments. In a good inductive argument, the truth of the premises provides some degree of support for the truth of the conclusion, where this degree-of-support might be measured via some numerical scale. By analogy with the notion of deductive entailment, the notion of inductive degree-of-support might mean something like this: among the logically possible states of affairs that make the premises true, the conclusion must be true in (at least) proportion r of them—where r is some numerical measure of the support strength.

If a logic of good inductive arguments is to be of any real value, the measure of support it articulates should be up to the task. Presumably, the logic should at least satisfy the following condition:

Criterion of Adequacy (CoA) : The logic should make it likely (as a matter of logic) that as evidence accumulates, the total body of true evidence claims will eventually come to indicate, via the logic’s measure of support , that false hypotheses are probably false and that true hypotheses are probably true.

The CoA stated here may strike some readers as surprisingly strong. Given a specific logic of evidential support, how might it be shown to satisfy such a condition? Section 4 will show precisely how this condition is satisfied by the logic of evidential support articulated in Sections 1 through 3 of this article.

This article will focus on the kind of the approach to inductive logic most widely studied by epistemologists and logicians in recent years. This approach employs conditional probability functions to represent measures of the degree to which evidence statements support hypotheses. Presumably, hypotheses should be empirically evaluated based on what they say (or imply) about the likelihood that evidence claims will be true. A straightforward theorem of probability theory, called Bayes’ Theorem, articulates the way in which what hypotheses say about the likelihoods of evidence claims influences the degree to which hypotheses are supported by those evidence claims. Thus, this approach to the logic of evidential support is often called a Bayesian Inductive Logic or a Bayesian Confirmation Theory . This article will first provide a detailed explication of a Bayesian approach to inductive logic. It will then examine the extent to which this logic may pass muster as an adequate logic of evidential support for hypotheses. In particular, we will see how such a logic may be shown to satisfy the Criterion of Adequacy stated above.

Sections 1 through 3 present all of the main ideas underlying the (Bayesian) probabilistic logic of evidential support. These three sections should suffice to provide an adequate understanding of the subject. Section 5 extends this account to cases where the implications of hypotheses about evidence claims (called likelihoods ) are vague or imprecise. After reading Sections 1 through 3, the reader may safely skip directly to Section 5, bypassing the rather technical account in Section 4 of how how the CoA is satisfied.

Section 4 is for the more advanced reader who wants an understanding of how this logic may bring about convergence to the true hypothesis as evidence accumulates. This result shows that the Criterion of Adequacy is indeed satisfied—that as evidence accumulates, false hypotheses will very probably come to have evidential support values (as measured by their posterior probabilities ) that approach 0; and as this happens, a true hypothesis may very probably acquire evidential support values (as measured by its posterior probability ) that approaches 1.

1. Inductive Arguments

2.1 the historical origins of probabilistic logic, 2.2 probabilistic logic: axioms and characteristics, 2.3 two conceptions of inductive probability, 3.1 likelihoods, 3.2 posterior probabilities and prior probabilities, 3.3 bayes’ theorem, 3.4 on prior probabilities and representations of vague and diverse plausibility assessments, 4.1 the space of possible outcomes of experiments and observations, 4.2 probabilistic independence, 4.3 likelihood ratio convergence when falsifying outcomes are possible, 4.4 likelihood ratio convergence when no falsifying outcomes are possible, 5. when the likelihoods are vague or diverse, list of supplements, other internet resources, related entries.

Let us begin by considering some common kinds of examples of inductive arguments. Consider the following two arguments:

Example 1. Every raven in a random sample of 3200 ravens is black. This strongly supports the following conclusion: All ravens are black.

Example 2. 62 percent of voters in a random sample of 400 registered voters (polled on February 20, 2004) said that they favor John Kerry over George W. Bush for President in the 2004 Presidential election. This supports with a probability of at least .95 the following conclusion: Between 57 percent and 67 percent of all registered voters favor Kerry over Bush for President (at or around the time the poll was taken).

This kind of argument is often called an induction by enumeration . It is closely related to the technique of statistical estimation. We may represent the logical form of such arguments semi-formally as follows:

Premise: In random sample S consisting of n members of population B , the proportion of members that have attribute A is r .

Therefore, with degree of support p ,

Conclusion: The proportion of all members of B that have attribute A is between \(r-q\) and \(r+q\) (i.e., lies within margin of error q of r ).

Let’s lay out this argument more formally. The premise breaks down into three separate statements: [ 1 ]

Any inductive logic that treats such arguments should address two challenges. (1) It should tell us which enumerative inductive arguments should count as good inductive arguments. In particular, it should tell us how to determine the appropriate degree p to which such premises inductively support the conclusion, for a given margin of error q . (2) It should demonstrably satisfy the CoA . That is, it should be provable (as a metatheorem) that if a conclusion expressing the approximate proportion for an attribute in a population is true, then it is very likely that sufficiently numerous random samples of the population will provide true premises for good inductive arguments that confer degrees of support p approaching 1 for that true conclusion—where, on pain of triviality, these sufficiently numerous samples are only a tiny fraction of a large population. The supplement on Enumerative Inductions: Bayesian Estimation and Convergence , shows precisely how a a Bayesian account of enumerative induction may meet these two challenges.

Enumerative induction is, however, rather limited in scope. This form of induction is only applicable to the support of claims involving simple universal conditionals (i.e., claims of form ‘All B s are A s’) and claims about the proportion of an attribute in a population (i.e., claims of form ‘the frequency of A s among the B s is r ’). But, many important empirical hypotheses are not reducible to this simple form, and the evidence for these hypotheses is not composed of an enumeration of such instances. Consider, for example, the Newtonian Theory of Mechanics:

All objects remain at rest or in uniform motion unless acted upon by some external force. An object’s acceleration (i.e., the rate at which its motion changes from rest or from uniform motion) is in the same direction as the force exerted on it; and the rate at which the object accelerates due to a force is equal to the magnitude of the force divided by the object’s mass. If an object exerts a force on another object, the second object exerts an equal amount of force on the first object, but in the opposite direction to the force exerted by the first object.

The evidence for (and against) this theory is not gotten by examining a randomly selected subset of objects and the forces acting upon them. Rather, the theory is tested by calculating what this theory says (or implies) about observable phenomena in a wide variety of specific situations—e.g., ranging from simple collisions between small bodies to the trajectories of planets and comets—and then seeing whether those phenomena occur in the way that the theory says they will. This approach to testing hypotheses and theories is ubiquitous, and should be captured by an adequate inductive logic.

More generally, for a wide range of cases where inductive reasoning is important, enumerative induction is inadequate. Rather, the kind of evidential reasoning that judges the likely truth of hypotheses on the basis of what they say (or imply) about the evidence is more appropriate. Consider the kinds of inferences jury members are supposed to make, based on the evidence presented at a murder trial. The inference to probable guilt or innocence is based on a patchwork of evidence of various kinds. It almost never involves consideration of a randomly selected sequences of past situations when people like the accused committed similar murders. Or, consider how a doctor diagnoses her patient on the basis of his symptoms. Although the frequency of occurrence of various diseases when similar symptoms have been present may play a role, this is clearly not the whole story. Diagnosticians commonly employ a form of hypothesis evaluation —e.g., would the hypothesis that the patient has a brain tumor account for his symptoms?; or are these symptoms more likely the result of a minor stroke?; or may some other hypothesis better account for the patient’s symptoms? Thus, a fully adequate account of inductive logic should explicate the logic of hypothesis evaluation , through which a hypothesis or theory may be tested on the basis of what it says (or "predicts") about observable phenomena. In Section 3 we will see how a kind of probabilistic inductive logic called "Bayesian Inference" or "Bayesian Confirmation Theory" captures such reasoning. The full logical structure of such arguments will be spelled out in that section.

2. Inductive Logic and Inductive Probabilities

Perhaps the oldest and best understood way of representing partial belief, uncertain inference, and inductive support is in terms of probability and the equivalent notion odds . Mathematicians have studied probability for over 350 years, but the concept is certainly much older. In recent times a number of other, related representations of partial belief and uncertain inference have emerged. Some of these approaches have found useful application in computer based artificial intelligence systems that perform inductive inferences in expert domains such as medical diagnosis. Nevertheless, probabilistic representations have predominated in such application domains. So, in this article we will focus exclusively on probabilistic representations of inductive support. A brief comparative description of some of the most prominent alternative representations of uncertainty and support-strength can be found in the supplement Some Prominent Approaches to the Representation of Uncertain Inference .

The mathematical study of probability originated with Blaise Pascal and Pierre de Fermat in the mid-17 th century. From that time through the early 19 th century, as the mathematical theory continued to develop, probability theory was primarily applied to the assessment of risk in games of chance and to drawing simple statistical inferences about characteristics of large populations—e.g., to compute appropriate life insurance premiums based on mortality rates. In the early 19 th century Pierre de Laplace made further theoretical advances and showed how to apply probabilistic reasoning to a much wider range of scientific and practical problems. Since that time probability has become an indispensable tool in the sciences, business, and many other areas of modern life.

Throughout the development of probability theory various researchers appear to have thought of it as a kind of logic. But the first extended treatment of probability as an explicit part of logic was George Boole’s The Laws of Thought (1854). John Venn followed two decades later with an alternative empirical frequentist account of probability in The Logic of Chance (1876). Not long after that the whole discipline of logic was transformed by new developments in deductive logic.

In the late 19 th and early 20 th century Frege, followed by Russell and Whitehead, showed how deductive logic may be represented in the kind of rigorous formal system we now call quantified predicate logic . For the first time logicians had a fully formal deductive logic powerful enough to represent all valid deductive arguments that arise in mathematics and the sciences. In this logic the validity of deductive arguments depends only on the logical structure of the sentences involved. This development in deductive logic spurred some logicians to attempt to apply a similar approach to inductive reasoning. The idea was to extend the deductive entailment relation to a notion of probabilistic entailment for cases where premises provide less than conclusive support for conclusions. These partial entailments are expressed in terms of conditional probabilities , probabilities of the form \(P[C \pmid B] = r\) (read “the probability of C given B is r ”), where P is a probability function, C is a conclusion sentence, B is a conjunction of premise sentences, and r is the probabilistic degree of support that premises B provide for conclusion C . Attempts to develop such a logic vary somewhat with regard to the ways in which they attempt to emulate the paradigm of formal deductive logic.

Some inductive logicians have tried to follow the deductive paradigm by attempting to specify inductive support probabilities solely in terms of the syntactic structures of premise and conclusion sentences. In deductive logic the syntactic structure of the sentences involved completely determines whether premises logically entail a conclusion. So these inductive logicians have attempted to follow suit. In such a system each sentence confers a syntactically specified degree of support on each of the other sentences of the language. Thus, the inductive probabilities in such a system are logical in the sense that they depend on syntactic structure alone. This kind of conception was articulated to some extent by John Maynard Keynes in his Treatise on Probability (1921). Rudolf Carnap pursued this idea with greater rigor in his Logical Foundations of Probability (1950) and in several subsequent works (e.g., Carnap 1952). (For details of Carnap’s approach see the section on logical probability in the entry on interpretations of the probability calculus , in this Encyclopedia .)

In the inductive logics of Keynes and Carnap, Bayes’ theorem, a straightforward theorem of probability theory, plays a central role in expressing how evidence comes to bear on hypotheses. Bayes’ theorem expresses how the probability of a hypothesis h on the evidence e , \(P[h \pmid e]\), depends on the probability that e should occur if h is true, \(P[e \pmid h]\), and on the probability of hypothesis h prior to taking the evidence into account, \(P[h]\) (called the prior probability of h ). (Later we’ll examine Bayes’ theorem in detail.) So, such approaches might well be called Bayesian logicist inductive logics. Other prominent Bayesian logicist attempts to develop a probabilistic inductive logic include the works of Jeffreys (1939), Jaynes (1968), and Rosenkrantz (1981).

It is now widely held that the core idea of this syntactic approach to Bayesian logicism is fatally flawed—that syntactic logical structure cannot be the sole determiner of the degree to which premises inductively support conclusions. A crucial facet of the problem faced by syntactic Bayesian logicism involves how the logic is supposed to apply in scientific contexts where the conclusion sentence is some scientific hypothesis or theory, and the premises are evidence claims. The difficulty is that in any probabilistic logic that satisfies the usual axioms for probabilities, the inductive support for a hypothesis must depend in part on its prior probability . This prior probability represents (arguably) how plausible the hypothesis is taken to be on the basis of considerations other than the observational and experimental evidence (e.g., perhaps due to various plausibility arguments). A syntactic Bayesian logicist must tell us how to assign values to these pre-evidential prior probabilities of hypotheses in a way that relies only on the syntactic logical structure of the hypothesis, perhaps based on some measure of syntactic simplicity. There are severe problems with getting this idea to work. Various kinds of examples seem to show that such an approach must assign intuitively quite unreasonable prior probabilities to hypotheses in specific cases (see the footnote cited near the end of Section 3.2 for details). Furthermore, for this idea to apply to the evidential support of real scientific theories, scientists would have to formalize theories in a way that makes their relevant syntactic structures apparent, and then evaluate theories solely on that syntactic basis (together with their syntactic relationships to evidence statements). Are we to evaluate alternative theories of gravitation, and alternative quantum theories, this way? This seems an extremely dubious approach to the evaluation of real scientific hypotheses and theories. Thus, it seems that logical structure alone may not suffice for the inductive evaluation of scientific hypotheses. (This issue will be treated in more detail in Section 3 , after we first see how probabilistic logics employ Bayes’ theorem to represent the evidential support for hypotheses as a function of prior probabilities together with evidential likelihoods .)

At about the time that the syntactic Bayesian logicist idea was developing, an alternative conception of probabilistic inductive reasoning was also emerging. This approach is now generally referred to as the Bayesian subjectivist or personalist approach to inductive reasoning (see, e.g., Ramsey 1926; De Finetti 1937; Savage 1954; Edwards, Lindman, & Savage 1963; Jeffrey 1983, 1992; Howson & Urbach 1993; Joyce 1999). This approach treats inductive probability as a measure of an agent’s degree-of-belief that a hypothesis is true, given the truth of the evidence. This approach was originally developed as part of a larger normative theory of belief and action known as Bayesian decision theory . The principal idea is that the strength of an agent’s desires for various possible outcomes should combine with her belief-strengths regarding claims about the world to produce optimally rational decisions. Bayesian subjectivists provide a logic of decision that captures this idea, and they attempt to justify this logic by showing that in principle it leads to optimal decisions about which of various risky alternatives should be pursued. On the Bayesian subjectivist or personalist account of inductive probability, inductive probability functions represent the subjective (or personal) belief-strengths of ideally rational agents, the kind of belief strengths that figure into rational decision making. (See the section on subjective probability in the entry on interpretations of the probability calculus , in this Encyclopedia .)

Elements of a logicist conception of inductive logic live on today as part of the general approach called Bayesian inductive logic . However, among philosophers and statisticians the term ‘Bayesian’ is now most closely associated with the subjectivist or personalist account of belief and decision. And the term ‘Bayesian inductive logic’ has come to carry the connotation of a logic that involves purely subjective probabilities. This usage is misleading since, for inductive logics, the Bayesian/non-Bayesian distinction should really turn on whether the logic gives Bayes’ theorem a prominent role, or the approach largely eschews the use of Bayes’ theorem in inductive inferences, as do the classical approaches to statistical inference developed by R. A. Fisher (1922) and by Neyman & Pearson (1967)). Indeed, any inductive logic that employs the same probability functions to represent both the probabilities of evidence claims due to hypotheses and the probabilities of hypotheses due to those evidence claims must be a Bayesian inductive logic in this broader sense; because Bayes’ theorem follows directly from the axioms that each probability function must satisfy, and Bayes’ theorem expresses a necessary connection between the probabilities of evidence claims due to hypotheses and the probabilities of hypotheses due to those evidence claims .

In this article the probabilistic inductive logic we will examine is a Bayesian inductive logic in this broader sense. This logic will not presuppose the subjectivist Bayesian theory of belief and decision, and will avoid the objectionable features of the syntactic version of Bayesian logicism. We will see that there are good reasons to distinguish inductive probabilities from degree-of-belief probabilities and from purely syntactic logical probabilities . So, the probabilistic logic articulated in this article will be presented in a way that depends on neither of these conceptions of what the probability functions are . However, this version of the logic will be general enough that it may be fitted to a Bayesian subjectivist or Bayesian syntactic-logicist program, if one desires to do that.

All logics derive from the meanings of terms in sentences. What we now recognize as formal deductive logic rests on the meanings (i.e., the truth-functional properties) of the standard logical terms. These logical terms, and the symbols we will employ to represent them, are as follows:

• ‘not’, ‘\({\nsim}\)’;
• ‘and’, ‘\(\cdot\)’;
• ‘inclusive or’, ‘\(\vee\)’;
• truth-functional ‘if-then’, ‘\(\supset\)’;
• ‘if and only if’, ‘\(\equiv\)’;
• ‘all’, ‘\(\forall\)’, and
• ‘some’, ‘\(\exists\)’;
• the identity relation, ‘=’.

The meanings of all other terms, the non-logical terms such as names and predicate and relational expressions, are permitted to “float free”. That is, the logical validity of deductive arguments depends neither on the meanings of the name and predicate and relation terms, nor on the truth-values of sentences containing them. It merely supposes that these non-logical terms are meaningful, and that sentences containing them have truth-values. Deductive logic then tells us that the logical structures of some sentences—i.e., the syntactic arrangements of their logical terms—preclude them from being jointly true of any possible state of affairs. This is the notion of logical inconsistency . The notion of logical entailment is inter-definable with it. A collection of premise sentences logically entails a conclusion sentence just when the negation of the conclusion is logically inconsistent with those premises.

An inductive logic must, it seems, deviate from the paradigm provided by deductive logic in several significant ways. For one thing, logical entailment is an absolute, all-or-nothing relationship between sentences, whereas inductive support comes in degrees-of-strength. For another, although the notion of inductive support is analogous to the deductive notion of logical entailment , and is arguably an extension of it, there seems to be no inductive logic extension of the notion of logical inconsistency —at least none that is inter-definable with inductive support in the way that logical inconsistency is inter-definable with logical entailment . Indeed, it turns out that when the unconditional probability of \((B\cdot{\nsim}A)\) is very nearly 0 (i.e., when \((B\cdot{\nsim}A)\) is “nearly inconsistent”), the degree to which B inductively supports A , \(P[A \pmid B]\), may range anywhere between 0 and 1.

Another notable difference is that when B logically entails A , adding a premise C cannot undermine the logical entailment—i.e., \((C\cdot B)\) must logically entail A as well. This property of logical entailment is called monotonicity . But inductive support is nonmonotonic . In general, depending on what \(A, B\), and C mean, adding a premise C to B may substantially raise the degree of support for A , or may substantially lower it, or may leave it completely unchanged—i.e., \(P[A \pmid (C\cdot B)]\) may have a value much larger than \(P[A \pmid B]\), or may have a much smaller value, or it may have the same, or nearly the same value as \(P[A \pmid B]\).

In a formal treatment of probabilistic inductive logic, inductive support is represented by conditional probability functions defined on sentences of a formal language L . These conditional probability functions are constrained by certain rules or axioms that are sensitive to the meanings of the logical terms (i.e., ‘not’, ‘and’, ‘or’, etc., the quantifiers ‘all’ and ‘some’, and the identity relation). The axioms apply without regard for what the other terms of the language may mean. In essence the axioms specify a family of possible support functions , \(\{P_{\beta}, P_{\gamma}, \ldots ,P_{\delta}, \ldots \}\) for a given language L . Although each support function satisfies these same axioms, the further issue of which among them provides an appropriate measure of inductive support is not settled by the axioms alone. That may depend on additional factors, such as the meanings of the non-logical terms (i.e., the names and predicate expressions) of the language.

A good way to specify the axioms of the logic of inductive support functions is as follows. These axioms are apparently weaker than the usual axioms for conditional probabilities. For instance, the usual axioms assume that conditional probability values are restricted to real numbers between 0 and 1. The following axioms do not assume this, but only that support functions assign some real numbers as values for support strengths. However, it turns out that the following axioms suffice to derive all the usual axioms for conditional probabilities (including the usual restriction to values between 0 and 1). We draw on these weaker axioms only to forestall some concerns about whether the support function axioms may assume too much, or may be overly restrictive.

Let L be a language for predicate logic with identity, and let ‘\(\vDash\)’ be the standard logical entailment relation—i.e., the expression ‘\(B \vDash A\)’ says “ B logically entails A ” and the expression ‘\(\vDash A\)’ says “ A is a tautology”. A support function is a function \(P_{\alpha}\) from pairs of sentences of L to real numbers that satisfies the following axioms:

• (1) \(P_{\alpha}[E \pmid F] \ne P_{\alpha}[G \pmid H]\) for at least some sentences \(E, F, G\), and H .

For all sentence \(A, B, C\), and D :

• (2) If \(B \vDash A\), then \(P_{\alpha}[A \pmid B] \ge P_{\alpha}[C \pmid D]\);
• (3) \(P_{\alpha}[A \pmid (B \cdot C)] = P_{\alpha}[A \pmid (C \cdot B)]\);
• (4) If \(C \vDash{\nsim}(B \cdot A)\), then either \[P_{\alpha}[(A \vee B) \pmid C] = P_{\alpha}[A \pmid C] + P_{\alpha}[B \pmid C]\] or else \[P_{\alpha}[E \pmid C] = P_{\alpha}[C \pmid C]\] for every sentence E ;
• (5) \(P_{\alpha}[(A \cdot B) \pmid C] = P_{\alpha}[A \pmid (B \cdot C)] \times P_{\alpha}[B \pmid C]\).

This axiomatization takes conditional probability as basic, as seems appropriate for evidential support functions . (These functions agree with the more usual unconditional probability functions when the latter are defined—just let \(P_{\alpha}[A] = P_{\alpha}[A \pmid (D \vee{\nsim}D)]\). However, these axioms permit conditional probabilities \(P_{\alpha}[A \pmid C]\) to remain defined even when condition statement C has probability 0—i.e., even when \(P_{\alpha}[C \pmid (D\vee{\nsim}D)] = 0\).)

Notice that conditional probability functions apply only to pairs of sentences, a conclusion sentence and a premise sentence. So, in probabilistic inductive logic we represent finite collections of premises by conjoining them into a single sentence. Rather than say,

A is supported to degree r by the set of premises \(\{B_1\), \(B_2\), \(B_3\),…, \(B_n\}\),

we instead say that

A is supported to degree r by the conjunctive premise \((((B_1\cdot B_2)\cdot B_3)\cdot \ldots \cdot B_n)\),

and write this as

The above axioms are quite weak. For instance, they do not say that logically equivalent sentences are supported by all other sentences to the same degree; rather, that result is derivable from these axioms (see result 6 below). Nor do these axioms say that logically equivalent sentences support all other sentences to the same degree; rather, that result is also derivable (see result 8 below). Indeed, from these axioms all of the usual theorems of probability theory may be derived. The following results are particularly useful in probabilistic logic. Their derivations from these axioms are provided in note 2. [ 2 ]

• If \(B \vDash A\), then \(P_{\alpha}[A \pmid B] = 1\).
• If \(C \vDash{\nsim}(B\cdot A)\), then either \[P_{\alpha}[(A \vee B) \pmid C] = P_{\alpha}[A \pmid C] + P_{\alpha}[B \pmid C]\] or else \(P_{\alpha}[E \pmid C] = 1\) for every sentence E .
• \(P_{\alpha}[{\nsim}A \pmid B] = 1 - P_{\alpha}[A \pmid B]\) or else \(P_{\alpha}[C \pmid B] = 1\) for every sentence C .
• \(1 \ge P_{\alpha}[A \pmid B] \ge 0\).
• If \(B \vDash A\), then \(P_{\alpha}[A \pmid C] \ge P_{\alpha}[B \pmid C]\).
• If \(B \vDash A\) and \(A \vDash B\), then \(P_{\alpha}[A \pmid C] = P_{\alpha}[B \pmid C]\).
• If \(C \vDash B\), then \(P_{\alpha}[(A\cdot B) \pmid C] = P_{\alpha}[(B\cdot A) \pmid C] = P_{\alpha}[A \pmid C]\).
• If \(C \vDash B\) and \(B \vDash C\), then \(P_{\alpha}[A \pmid B] = P_{\alpha}[A \pmid C]\).
• \(P_{\alpha}[B \pmid C] \gt 0\), then \[P_{\alpha}[A \pmid (B\cdot C)] = P_{\alpha}[B \pmid (A\cdot C)] \times \frac{P_{\alpha}[A \pmid C]}{P_{\alpha}[B \pmid C]}\] (this is a simple form of Bayes’ theorem).
• \(P_{\alpha}[(A\vee B) \pmid C] = P_{\alpha}[A \pmid C] + P_{\alpha}[B \pmid C] - P_{\alpha}[(A\cdot B) \pmid C]\).
• If \(\{B_1 , \ldots ,B_n\}\) is any finite set of sentences such that for each pair \(B_i\) and \(B_j, C \vDash{\nsim}(B_{i}\cdot B_{j})\) (i.e., the members of the set are mutually exclusive, given C ), then either \(P_{\alpha}[D \pmid C] = 1\) for every sentence D , or \[ P_{\alpha}[((B_1\vee B_2)\vee \ldots \vee B_n) \pmid C] = \sum ^{n}_{i=1} P_{\alpha}[B_i \pmid C]. \]
• If \(\{B_1 , \ldots ,B_n , \ldots \}\) is any countably infinite set of sentences such that for each pair \(B_i\) and \(B_j, C \vDash{\nsim}(B_{i}\cdot B_{j})\), then either \(P_{\alpha}[D \pmid C] = 1\) for every sentence D , or [ 3 ] \[ \lim_n P_{\alpha}[((B_1\vee B_2)\vee \ldots \vee B_n) \pmid C] = \sum^{\infty}_{i=1} P_{\alpha}[B_i \pmid C]. \]

Let us now briefly consider each axiom to see how plausible it is as a constraint on a quantitative measure of inductive support, and how it extends the notion of deductive entailment. First notice that each degree-of-support function \(P_{\alpha}\) on L measures support strength with some real number values, but the axioms don’t explicitly restrict these values to lie between 0 and 1. It turns out that the all support values must lie between 0 and 1, but this follows from the axioms, rather than being assumed by them. The scaling of inductive support via the real numbers is surely a reasonable way to go.

Axiom 1 is a non-triviality requirement. It says that the support values cannot be the same for all sentence pairs. This axiom merely rules out the trivial support function that assigns the same amount of support to each sentence by every sentence. One might replace this axiom with the following rule:

But this alternative rule turns out to be derivable from axiom 1 together with the other axioms.

Axiom 2 asserts that when B logically entail A , the support of A by B is as strong as support can possibly be. This comports with the idea that an inductive support function is a generalization of the deductive entailment relation, where the premises of deductive entailments provide the strongest possible support for their conclusions.

Axiom 3 merely says that \((B \cdot C)\) supports sentences to precisely the same degree that \((C \cdot B)\) supports them. This is an especially weak axiom. But taken together with the other axioms, it suffices to entail that logically equivalent sentences support all sentences to precisely the same degree.

Axiom 4 says that inductive support adds up in a plausible way. When C logically entails the incompatibility of A and B , i.e., when no possible state of affairs can make both A and B true together, the degrees of support that C provides to each of them individually must sum to the support it provides to their disjunction. The only exception is in those cases where C acts like a logical contradiction and supports all sentences to the maximum possible degree (in deductive logic a logical contradiction logically entails every sentence).

To understand what axiom 5 says, think of a support function \(P_{\alpha}\) as describing a measure on possible states of affairs. Read each degree-of-support expression of form ‘\(P_{\alpha}[D \pmid E] = r\)’ to say that the proportion of states of affairs in which D is true among those states of affairs where E is true is r . Read this way, axiom 5 then says the following. Suppose B is true in proportion q of all the states of affairs where C is true, and suppose A is true in fraction r of those states where B and C are true together. Then A and B should be true together in what proportion of all the states where C is true? In fraction r (the \((A\cdot B)\) part) of proportion q (the B portion) of all those states where C is true.

The degree to which a sentence B supports a sentence A may well depend on what these sentences mean. In particular it will usually depend on the meanings we associate with the non-logical terms (those terms other than the logical terms not , and , or , etc., the quantifiers , and identity ), that is, on the meanings of the names, and the predicate and relation terms of the language. For example, we should want

given the usual meanings of ‘bachelor’ and ‘married’, since “all bachelors are unmarried” is analytically true—i.e. no empirical evidence is required to establish this connection. (In the formal language for predicate logic, if we associate the meaning “is married” with predicate term ‘ M ’, the meaning “is a bachelor” with the predicate term ‘ B ’, and take the name term ‘ g ’ to refer to George, then we should want \(P_{\alpha}[{\nsim}Mg \pmid Bg] = 1\), since \(\forall x (Bx \supset{\nsim}Mx)\) is analytically true on this meaning assignment to the non-logical terms.) So, let’s associate with each individual support function \(P_{\alpha}\) a specific assignment of meanings ( primary intensions ) to all the non-logical terms of the language. (However, evidential support functions should not presuppose meaning assignments in the sense of so-called secondary intensions —e.g., those associated with rigid designators across possible states of affairs. For, we should not want a confirmation function \(P_{\alpha}\) to make

since we presumably want the inductive logic to draw on explicit empirical evidence to support the claim that water is made of H 2 O. Thus, the meanings of terms we associate with a support function should only be their primary intensions, not their secondary intensions.)

In the context of inductive logic it makes good sense to supplement the above axioms with two additional axioms. Here is the first of them:

• (6) If A is an axiom of set theory or any other piece of pure mathematics employed by the sciences, or if A is analytically true (i.e., if the truth of A depends only on the meanings of the words it contains, where the specific meanings for names and predicates are those associated with the particular support function \(P_{\alpha})\), then, for all sentences C , \(P_{\alpha}[A \pmid C] = P_{\alpha}[C \pmid C]\) (i.e., \(P_{\alpha}[A \pmid C] = 1)\).

Here is how axiom 6 applies to the above example, yielding \(P_{\alpha}[{\nsim}Mg \pmid Bg] = 1\) when the meaning assignments to non-logical terms associated with support function \(P_{\alpha}\) makes \(\forall x(Bx \supset{\nsim}Mx)\) analytically true. From axiom 6 (followed by results 7, 5, and 4) we have

thus, \(P_{\alpha}[{\nsim}Mg \pmid Bg] = 1\). The idea behind axiom 6 is that inductive logic is about evidential support for contingent claims. Nothing can count as empirical evidence for or against non-contingent truths. In particular, analytic truths should be maximally supported by all premises C .

One important respect in which inductive logic should follow the deductive paradigm is that the logic should not presuppose the truth of contingent statements. If a statement C is contingent, then some other statements should be able to count as evidence against C . Otherwise, a support function \(P_{\alpha}\) will take C and all of its logical consequences to be supported to degree 1 by all possible evidence claims. This is no way for an inductive logic to behave. The whole idea of inductive logic is to provide a measure of the extent to which premise statements indicate the likely truth-values of contingent conclusion statements. This idea won’t work properly if the truth-values of some contingent statements are presupposed by assigning them support value 1 on every possible premise. Such probability assignments would make the inductive logic enthymematic by hiding significant premises in inductive support relationships. It would be analogous to permitting deductive arguments to count as valid in cases where the explicitly stated premises are insufficient to logically entail the conclusion, but where the validity of the argument is permitted to depend on additional unstated premises. This is not how a rigorous approach to deductive logic should work, and it should not be a common practice in a rigorous approach to inductive logic.

Nevertheless, it is common practice for probabilistic logicians to sweep provisionally accepted contingent claims under the rug by assigning them probability 1 (regardless of the fact that no explicit evidence for them is provided). This practice saves the trouble of repeatedly writing a given contingent sentence B as a premise, since \(P_{\gamma}[A \pmid B\cdot C]\) will equal \(P_{\gamma}[A \pmid C]\) whenever \(P_{\gamma}[B \pmid C] = 1\). Although this convention is useful, such probability functions should be considered mere abbreviations for proper, logically explicit, non-enthymematic, inductive support relations. Thus, properly speaking, an inductive support function \(P_{\alpha}\) should not assign probability 1 to a sentence on every possible premise unless that sentence is either (i) logically true, or (ii) an axiom of set theory or some other piece of pure mathematics employed by the sciences, or (iii) unless according to the interpretation of the language that \(P_{\alpha}\) presupposes, the sentence is analytic (and so outside the realm of evidential support). Thus, we adopt the following version of the so-called “axiom of regularity”.

• (7) If, for all C , \(P_{\alpha}[A \pmid C] = P_{\alpha}[C \pmid C]\) (i.e., \(P_{\alpha}[A \pmid C] = 1\)), then A must be a logical truth or an axiom of set theory or some other piece of pure mathematics employed by the sciences, or A must be analytically true (according to the meanings of the terms of L associated with support function \(P_{\alpha})\).

Axioms 6 and 7 taken together say that a support function \(P_{\alpha}\) counts as non-contingently true, and so not subject to empirical support, just those sentences that are assigned probability 1 by every premise.

Some Bayesian logicists have proposed that an inductive logic might be made to depend solely on the logical form of sentences, as is the case for deductive logic. The idea is, effectively, to supplement axioms 1–7 with additional axioms that depend only on the logical structures of sentences, and to introduce enough such axioms to reduce the number of possible support functions to a single uniquely best support function. It is now widely agreed that this project cannot be carried out in a plausible way. Perhaps support functions should obey some rules in addition to axioms 1–7. But it is doubtful that any plausible collection of additional rules can suffice to determine a single, uniquely qualified support function. Later, in Section 3 , we will briefly return to this issue, after we develop a more detailed account of how inductive probabilities capture the relationship between hypotheses and evidence.

Axioms 1–7 for conditional probability functions merely place formal constraints on what may properly count as a degree of support function . Each function \(P_{\alpha}\) that satisfies these axioms may be viewed as a possible way of applying the notion of inductive support to a language L that respects the meanings of the logical terms, much as each possible truth-value assignment for a language represents a possible way of assigning truth-values to its sentences in a way that respects the meanings of the logical terms. The issue of which of the possible truth-value assignments to a language represents the actual truth or falsehood of its sentences depends on more than this. It depends on the meanings of the non-logical terms and on the state of the actual world. Similarly, the degree to which some sentences actually support others in a fully meaningful language must rely on something more than the mere satisfaction of the axioms for support functions. It must, at least, rely on what the sentences of the language mean, and perhaps on much more besides. But, what more? Perhaps a better understanding of what inductive probability is may provide some help by filling out our conception of what inductive support is about. Let’s pause to discuss two prominent views—two interpretations of the notion of inductive probability.

One kind of non-syntactic logicist reading of inductive probability takes each support function \(P_{\alpha}\) to be a measure on possible states of affairs. The idea is that, given a fully meaningful language (associated with support function \(P_{\alpha}\)) ‘\(P_{\alpha}[A \pmid B] = r\)’ says that among those states of affairs in which B is true, A is true in proportion r of them. There will not generally be a single privileged way to define such a measure on possible states of affairs. Rather, each of a number of functions \(P_{\alpha}\), \(P_{\beta}\), \(P_{\gamma}\),…, etc., that satisfy the constraints imposed by axioms 1–7 may represent a viable measure of the inferential import of the propositions expressed by sentences of the language. This idea needs more fleshing out, of course. The next section will provide some indication of how that might go.

Subjectivist Bayesians offer an alternative reading of the support functions. First, they usually take unconditional probability as basic, and take conditional probabilities as defined in terms of unconditional probabilities: the conditional probability ‘\(P_{\alpha}[A \pmid B]\)’ is defined as a ratio of unconditional probabilities:

Subjectivist Bayesians take each unconditional probability function \(P_{\alpha}\) to represent the belief-strengths or confidence-strengths of an ideally rational agent, \(\alpha\). On this understanding ‘\(P_{\alpha}[A] =r\)’ says, “the strength of \(\alpha\)’s belief (or confidence) that A is truth is r ”. Subjectivist Bayesians usually tie such belief strengths to how much money (or how many units of utility ) the agent would be willing to bet on A turning out to be true. Roughly, the idea is this. Suppose that an ideally rational agent \(\alpha\) would be willing to accept a wager that would yield (no less than) $ u if A turns out to be true and would lose him $1 if A turns out to be false. Then, under reasonable assumptions about the agent’s desire money, it can be shown that the agent’s belief strength that A is true should be

And it can further be shown that any function \(P_{\alpha}\) that expresses such betting-related belief-strengths on all statements in agent \(\alpha\)’s language must satisfy axioms for unconditional probabilities analogous to axioms 1–5. [ 4 ] Moreover, it can be shown that any function \(P_{\beta}\) that satisfies these axioms is a possible rational belief function for some ideally rational agent \(\beta\). These relationships between belief-strengths and the desirability of outcomes (e.g., gaining money or goods on bets) are at the core of subjectivist Bayesian decision theory . Subjectivist Bayesians usually take inductive probability to just be this notion of probabilistic belief-strength .

Undoubtedly real agents do believe some claims more strongly than others. And, arguably, the belief strengths of real agents can be measured on a probabilistic scale between 0 and 1, at least approximately. And clearly the inductive support of a hypothesis by evidence should influence the strength of an agent’s belief in the truth of that hypothesis—that’s the point of engaging in inductive reasoning, isn’t it? However, there is good reason for caution about viewing inductive support functions as Bayesian belief-strength functions, as we’ll see a bit later. So, perhaps an agent’s support function is not simply identical to his belief function, and perhaps the relationship between inductive support and belief-strength is somewhat more complicated.

In any case, some account of what support functions are supposed to represent is clearly needed. The belief function account and the logicist account (in terms of measures on possible states of affairs) are two attempts to provide this account. But let us put this interpretative issue aside for now. One may be able to get a better handle on what inductive support functions really are after one sees how the inductive logic that draws on them is supposed to work.

3. The Application of Inductive Probabilities to the Evaluation of Scientific Hypotheses

One of the most important applications of an inductive logic is its treatment of the evidential evaluation of scientific hypotheses. The logic should capture the structure of evidential support for all sorts of scientific hypotheses, ranging from simple diagnostic claims (e.g., “the patient is infected by the HIV”) to complex scientific theories about the fundamental nature of the world, such as quantum mechanics or the theory of relativity. This section will show how evidential support functions (a.k.a. Bayesian confirmation functions) represent the evidential evaluation of scientific hypotheses and theories. This logic is essentially comparative. The evaluation of a hypothesis depends on how strongly evidence supports it over alternative hypotheses.

Consider some collection of mutually incompatible, alternative hypotheses (or theories) about a common subject matter, \(\{h_1, h_2 , \ldots \}\). The collection of alternatives may be very simple, e.g., {“the patient has HIV”, “the patient is free of HIV”}. Or, when the physician is trying to determine which among a range of diseases is causing the patient’s symptoms, the collection of alternatives may consist of a long list of possible disease hypotheses. For the cosmologist, the collection of alternatives may consist of several distinct gravitational theories, or several empirically distinct variants of the “same” theory. Whenever two variants of a hypothesis (or theory) differ in empirical import, they count as distinct hypotheses. (This should not be confused with the converse positivistic assertion that theories with the same empirical content are really the same theory. Inductive logic doesn’t necessarily endorse that view.)

The collection of competing hypotheses (or theories) to be evaluated by the logic may be finite in number, or may be countably infinite. No realistic language contains more than a countable number of expressions; so it suffices for a logic to apply to countably infinite number of sentences. From a purely logical perspective the collection of competing alternatives may consist of every rival hypothesis (or theory) about a given subject matter that can be expressed within a given language — e.g., all possible theories of the origin and evolution of the universe expressible in English and contemporary mathematics. In practice, alternative hypotheses (or theories) will often be constructed and evidentially evaluated over a long period of time. The logic of evidential support works in much the same way regardless of whether all alternative hypotheses are considered together, or only a few alternative hypotheses are available at a time.

Evidence for scientific hypotheses consists of the results of specific experiments or observations. For a given experiment or observation, let ‘\(c\)’ represent a description of the relevant conditions under which it is performed, and let ‘\(e\)’ represent a description of the result of the experiment or observation, the evidential outcome of conditions \(c\).

The logical connection between scientific hypotheses and the evidence often requires the mediation of background information and auxiliary hypotheses. Let ‘\(b\)’ represent whatever background and auxiliary hypotheses are required to connect each hypothesis \(h_i\) among the competing hypotheses \(\{h_1, h_2 , \ldots \}\) to the evidence. Although the claims expressed by the auxiliary hypotheses within \(b\) may themselves be subject to empirical evaluation, they should be the kinds of claims that are not at issue in the evaluation of the alternative hypothesis in the collection \(\{h_1, h_2 , \ldots \}\). Rather, each of the alternative hypotheses under consideration draws on the same background and auxiliaries to logically connect to the evidential events. (If competing hypotheses \(h_i\) and \(h_j\) draw on distinct auxiliary hypotheses \(a_i\) and \(a_j\), respectively, in making logical contact with evidential claims, then the following treatment should be applied to the respective conjunctive hypotheses, \((h_{i}\cdot a_{i})\) and \((h_{j}\cdot a_{j})\), since these alternative conjunctive hypotheses will constitute the empirically distinct alternatives at issue.)

In cases where a hypothesis is deductively related to an outcome \(e\) of an observational or experimental condition \(c\) (via background and auxiliaries \(b\)), we will have either \(h_i\cdot b\cdot c \vDash e\) or \(h_i\cdot b\cdot c \vDash{\nsim}e\) . For example, \(h_i\) might be the Newtonian Theory of Gravitation. A test of the theory might involve a condition statement \(c\) that describes the results of some earlier measurements of Jupiter’s position, and that describes the means by which the next position measurement will be made; the outcome description \(e\) states the result of this additional position measurement; and the background information (and auxiliary hypotheses) \(b\) might state some already well confirmed theory about the workings and accuracy of the devices used to make the position measurements. Then, from \(h_i\cdot b\cdot c\) we may calculate the specific outcome \(e\) we expect to find; thus, the following logical entailment holds: \(h_i\cdot b\cdot c \vDash e\) . Then, provided that the experimental and observational conditions stated by \(c\) are in fact true, if the evidential outcome described by \(e\) actually occurs, the resulting conjoint evidential claim \((c\cdot e)\) may be considered good evidence for \(h_i\), given \(b\). (This method of theory evaluation is called the hypothetical-deductive approach to evidential support.) On the other hand, when from \(h_i\cdot b\cdot c\) we calculate some outcome incompatible with the observed evidential outcome \(e\), then the following logical entailment holds: \(h_i\cdot b\cdot c \vDash{\nsim}e\). In that case, from deductive logic alone we must also have that \(b\cdot c\cdot e \vDash{\nsim}h_i\) ; thus, \(h_i\) is said to be falsified by \(b\cdot c\cdot e\). The Bayesian account of evidential support we will be describing below extends this deductivist approach to include cases where the hypothesis \(h_i\) (and its alternatives) may not be deductive related to the evidence, but may instead imply that the evidential outcome is likely or unlikely to some specific degree r . That is, the Bayesian approach applies to cases where we may have neither \(h_i\cdot b\cdot c \vDash e\) nor \(h_i\cdot b\cdot c \vDash{\nsim}e\), but may instead only have \(P[e \pmid h_i\cdot b\cdot c] = r\), where r is some “entailment strength” between 0 and 1.

Before going on to describing the logic of evidential support in more detail, perhaps a few more words are in order about the background knowledge and auxiliary hypotheses, represented here by ‘\(b\)’. Duhem (1906) and Quine (1953) are generally credited with alerting inductive logicians to the importance of auxiliary hypotheses in connecting scientific hypotheses and theories to empirical evidence. (See the entry on Pierre Duhem .) They point out that scientific hypotheses often make little contact with evidence claims on their own. Rather, in most cases scientific hypotheses make testable predictions only relative to background information and auxiliary hypotheses that tie them to the evidence. (Some specific examples of such auxiliary hypotheses will be provided in the next subsection.) Typically auxiliaries are highly confirmed hypotheses from other scientific domains. They often describe the operating characteristics of various devices (e.g., measuring instruments) used to make observations or conduct experiments. Their credibility is usually not at issue in the testing of hypothesis \(h_i\) against its competitors, because \(h_i\) and its alternatives usually rely on the same auxiliary hypotheses to tie them to the evidence. But even when an auxiliary hypothesis is already well-confirmed, we cannot simply assume that it is unproblematic, or just known to be true . Rather, the evidential support or refutation of a hypothesis \(h_i\) is relative to whatever auxiliaries and background information (in \(b\)) is being supposed in the confirmational context. In other contexts the auxiliary hypotheses used to test \(h_i\) may themselves be among a collection of alternative hypotheses that are subject to evidential support or refutation. Furthermore, to the extent that competing hypotheses employ different auxiliary hypotheses in accounting for evidence, the evidence only tests each such hypothesis in conjunction with its distinct auxiliaries against alternative hypotheses packaged with their distinct auxiliaries, as described earlier. Thus, what counts as a hypothesis to be tested , \(h_i\), and what counts as auxiliary hypotheses and background information, \(b\), may depend on the epistemic context—on what class of alternative hypotheses are being tested by a collection of experiments or observations, and on what claims are presupposed in that context. No statement is intrinsically a test hypothesis , or intrinsically an auxiliary hypothesis or background condition . Rather, these categories are roles statements may play in a particular epistemic context.

In a probabilistic inductive logic the degree to which the evidence \((c\cdot e)\) supports a hypothesis \(h_i\) relative to background and auxiliaries \(b\) is represented by the posterior probability of \(h_i\), \(P_{\alpha}[h_i \pmid b\cdot c\cdot e]\), according to an evidential support function \(P_{\alpha}\). It turns out that the posterior probability of a hypothesis depends on just two kinds of factors: (1) its prior probability , \(P_{\alpha}[h_i \pmid b]\), together with the prior probabilities of its competitors, \(P_{\alpha}[h_j \pmid b]\), \(P_{\alpha}[h_k \pmid b]\), etc.; and (2) the likelihood of evidential outcomes \(e\) according to \(h_i\) in conjunction with with \(b\) and \(c\), \(P[e \pmid h_i\cdot b\cdot c]\), together with the likelihoods of these same evidential outcomes according to competing hypotheses, \(P[e \pmid h_j\cdot b\cdot c]\), \(P[e \pmid h_k\cdot b\cdot c]\), etc. We will now examine each of these factors in some detail. Following that we will see precisely how the values of posterior probabilities depend on the values of likelihoods and prior probabilities.

In probabilistic inductive logic the likelihoods carry the empirical import of hypotheses. A likelihood is a support function probability of form \(P[e \pmid h_i\cdot b\cdot c]\). It expresses how likely it is that outcome \(e\) will occur according to hypothesis \(h_i\) together with the background and auxiliaries \(b\) and the experimental (or observational) conditions \(c\). [ 5 ] If a hypothesis together with auxiliaries and experimental/observation conditions deductively entails an evidence claim, the axioms of probability make the corresponding likelihood objective in the sense that every support function must agree on its values: \(P[e \pmid h_i\cdot b\cdot c] = 1\) if \(h_i\cdot b\cdot c \vDash e\); \(P[e \pmid h_i\cdot b\cdot c] = 0\) if \(h_i\cdot b\cdot c \vDash{\nsim}e\). However, in many cases a hypothesis \(h_i\) will not be deductively related to the evidence, but will only imply it probabilistically. There are several ways this might happen: (1) hypothesis \(h_i\) may itself be an explicitly probabilistic or statistical hypothesis; (2) an auxiliary statistical hypothesis, as part of the background b , may connect hypothesis \(h_i\) to the evidence; (3) the connection between the hypothesis and the evidence may be somewhat loose or imprecise, not mediated by explicit statistical claims, but nevertheless objective enough for the purposes of evidential evaluation. Let’s briefly consider examples of the first two kinds. We’ll treat case (3) in Section 5 , which addresses the issue of vague and imprecise likelihoods.

The hypotheses being tested may themselves be statistical in nature. One of the simplest examples of statistical hypotheses and their role in likelihoods are hypotheses about the chance characteristic of coin-tossing. Let \(h_{[r]}\) be a hypothesis that says a specific coin has a propensity (or objective chance ) r for coming up heads on normal tosses, let \(b\) say that such tosses are probabilistically independent of one another. Let \(c\) state that the coin is tossed n times in the normal way; and let \(e\) say that on these tosses the coin comes up heads m times. In cases like this the value of the likelihood of the outcome \(e\) on hypothesis \(h_{[r]}\) for condition \(c\) is given by the well-known binomial formula:

There are, of course, more complex cases of likelihoods involving statistical hypotheses. Consider, for example, the hypothesis that plutonium 233 nuclei have a half-life of 20 minutes—i.e., that the propensity (or objective chance ) for a Pu-233 nucleus to decay within a 20 minute period is 1/2. The full statistical model for the lifetime of such a system says that the propensity (or objective chance ) for that system to remain intact (i.e., to not decay) within any time period x is governed by the formula \(1/2^{x/\tau}\), where \(\tau\) is the half-life of such a system. Let \(h\) be a hypothesis that says that this statistical model applies to Pu-233 nuclei with \(\tau = 20\) minutes; let \(c\) say that some specific Pu-233 nucleus is intact within a decay detector (of some specific kind) at an initial time \(t_0\); let \(e\) say that no decay of this same Pu-233 nucleus is detected by the later time \(t\); and let \(b\) say that the detector is completely accurate (it always registers a real decay, and it never registers false-positive detections). Then, the associated likelihood of \(e\) given \(h\) and \(c\) is this: \(P[e \pmid h\cdot b\cdot c] = 1/2^{(t - t_0)/\tau}\), where the value of \(\tau\) is 20 minutes.

An auxiliary statistical hypothesis, as part of the background \(b\), may be required to connect hypothesis \(h_i\) to the evidence. For example, a blood test for HIV has a known false-positive rate and a known true-positive rate. Suppose the false-positive rate is .05—i.e., the test tends to incorrectly show the blood sample to be positive for HIV in 5% of all cases where HIV is not present . And suppose that the true-positive rate is .99—i.e., the test tends to correctly show the blood sample to be positive for HIV in 99% of all cases where HIV really is present . When a particular patient’s blood is tested, the hypotheses under consideration are this patient is infected with HIV , \(h\), and this patient is not infected with HIV , \({\nsim}h\). In this context the known test characteristics function as background information, b . The experimental condition \(c\) merely states that this particular patient was subjected to this specific kind of blood test for HIV, which was processed by the lab using proper procedures. Let us suppose that the outcome \(e\) states that the result is a positive test result for HIV. The relevant likelihoods then, are \(P[e \pmid h\cdot b\cdot c] = .99\) and \(P[e \pmid {\nsim}h\cdot b\cdot c]\) = .05.

In this example the values of the likelihoods are entirely due to the statistical characteristics of the accuracy of the test, which is carried by the background/auxiliary information \(b\). The hypothesis \(h\) being tested by the evidence is not itself statistical.

This kind of situation may, of course, arise for much more complex hypotheses. The alternative hypotheses of interest may be deterministic physical theories, say Newtonian Gravitation Theory and some specific alternatives. Some of the experiments that test this theory relay on somewhat imprecise measurements that have known statistical error characteristics, which are expressed as part of the background or auxiliary hypotheses, \(b\). For example, the auxiliary \(b\) may describe the error characteristics of a device that measures the torque imparted to a quartz fiber, where the measured torque is used to assess the strength of the gravitational force between test masses. In that case \(b\) may say that for this kind of device the measurement errors are normally distributed about whatever value a given gravitational theory predicts, with some specified standard deviation that is characteristic of the device. This results in specific values \(r_i\) for the likelihoods, \(P[e \pmid h_i\cdot b\cdot c] = r_i\), for each of the various gravitational theories, \(h_i\), being tested.

Likelihoods that arise from explicit statistical claims—either within the hypotheses being tested, or from explicit statistical background claims that tie the hypotheses to the evidence—are often called direct inference likelihoods . Such likelihoods should be completely objective. So, all evidential support functions should agree on their values, just as all support functions agree on likelihoods when evidence is logically entailed. Direct inference likelihoods are logical in an extended, non-deductive sense. Indeed, some logicians have attempted to spell out the logic of direct inferences in terms of the logical form of the sentences involved. [ 6 ] But regardless of whether that project succeeds, it seems reasonable to take likelihoods of this sort to have highly objective or intersubjectively agreed values.

Not all likelihoods of interest in confirmational contexts are warranted deductively or by explicitly stated statistical claims. In such cases the likelihoods may have vague, imprecise values, but values that are determinate enough to still underwrite an objective evaluation of hypotheses on the evidence. In Section 5 we’ll consider such cases, where no underlying statistical theory is involved, but where likelihoods are determinate enough to play their standard role in the evidential evaluation of scientific hypotheses. However, the proper treatment of such cases will be more easily understood after we have first seen how the logic works when likelihoods are precisely known (such as cases where the likelihood values are endorsed by explicit statistical hypotheses and/or explicit statistical auxiliaries). In any case, the likelihoods that relate hypotheses to evidence claims in many scientific contexts will have such objective values. So, although a variety of different support functions \(P_{\alpha}\), \(P_{\beta}\),…, \(P_{\gamma}\), etc., may be needed to represent the differing “inductive proclivities” of the various members of a scientific community, for now we will consider cases where all evidential support functions agree on the values of the likelihoods. For, the likelihoods represent the empirical content of a scientific hypothesis, what the hypothesis (together with experimental conditions, \(c\), and background and auxiliaries \(b\)) says or probabilistically implies about the evidence. Thus, the empirical objectivity of a science relies on a high degree of objectivity or intersubjective agreement among scientists on the numerical values of likelihoods.

To see the point more vividly, imagine what a science would be like if scientists disagreed widely about the values of likelihoods. Each practitioner interprets a theory to say quite different things about how likely it is that various possible evidence statements will turn out to be true. Whereas scientist \(\alpha\) takes theory \(h_1\) to probabilistically imply that event \(e\) is highly likely, his colleague \(\beta\) understands the empirical import of \(h_1\) to say that \(e\) is very unlikely. And, conversely, \(\alpha\) takes competing theory \(h_2\) to probabilistically imply that \(e\) is very unlikely, whereas \(\beta\) reads \(h_2\) to say that \(e\) is extremely likely. So, for \(\alpha\) the evidential outcome \(e\) supplies strong support for \(h_1\) over \(h_2\), because

But his colleague \(\beta\) takes outcome \(e\) to show just the opposite, that \(h_2\) is strongly supported over \(h_1\), because

If this kind of situation were to occur often, or for significant evidence claims in a scientific domain, it would make a shambles of the empirical objectivity of that science. It would completely undermine the empirical testability of such hypotheses and theories within that scientific domain. Under these circumstances, although each scientist employs the same sentences to express a given theory \(h_i\), each understands the empirical import of these sentences so differently that \(h_i\) as understood by \(\alpha\) is an empirically different theory than \(h_i\) as understood by \(\beta\). (Indeed, arguably, \(\alpha\) must take at least one of the two sentences, \(h_1\) or \(h_2\), to express a different proposition than does \(\beta\).) Thus, the empirical objectivity of the sciences requires that experts should be in close agreement about the values of the likelihoods. [ 7 ]

For now we will suppose that the likelihoods have objective or intersubjectively agreed values, common to all agents in a scientific community. We mark this agreement by dropping the subscript ‘\(\alpha\)’, ‘\(\beta\)’, etc., from expressions that represent likelihoods, since all support functions under consideration are supposed to agree on the values for likelihoods. One might worry that this supposition is overly strong. There are legitimate scientific contexts where, although scientists should have enough of a common understanding of the empirical import of hypotheses to assign quite similar values to likelihoods, precise agreement on their numerical values may be unrealistic. This point is right in some important kinds of cases. So later, in Section 5, we will see how to relax the supposition that precise likelihood values are available, and see how the logic works in such cases. But for now the main ideas underlying probabilistic inductive logic will be more easily explained if we focus on those contexts were objective or intersubjectively agreed likelihoods are available. Later we will see that much the same logic continues to apply in contexts where the values of likelihoods may be somewhat vague, or where members of the scientific community disagree to some extent about their values.

An adequate treatment of the likelihoods calls for the introduction of one additional notational device. Scientific hypotheses are generally tested by a sequence of experiments or observations conducted over a period of time. To explicitly represent the accumulation of evidence, let the series of sentences \(c_1\), \(c_2\), …, \(c_n\), describe the conditions under which a sequence of experiments or observations are conducted. And let the corresponding outcomes of these observations be represented by sentences \(e_1\), \(e_2\), …, \(e_n\). We will abbreviate the conjunction of the first n descriptions of experimental or observational conditions by ‘\(c^n\)’, and abbreviate the conjunction of descriptions of their outcomes by ‘\(e^n\)’. Then, for a stream of n observations or experiments and their outcomes, the likelihoods take form \(P[e^n \pmid h_{i}\cdot b\cdot c^{n}] = r\), for appropriate values of \(r\). In many cases the likelihood of the evidence stream will be equal to the product of the likelihoods of the individual outcomes:

When this equality holds, the individual bits of evidence are said to be probabilistically independent on the hypothesis (together with auxiliaries) . In the following account of the logic of evidential support, such probabilistic independence will not be assumed, except in those places where it is explicitly invoked.

The probabilistic logic of evidential support represents the net support of a hypothesis by the posterior probability of the hypothesis , \(P_{\alpha}[h_i \pmid b\cdot c^{n}\cdot e^{n}]\). The posterior probability represents the net support for the hypothesis that results from the evidence, \(c^n \cdot e^n\), together with whatever plausibility considerations are taken to be relevant to the assessment of \(h_i\). Whereas the likelihoods are the means through which evidence contributes to the posterior probability of a hypothesis, all other relevant plausibility consideration are represented by a separate factor, called the prior probability of the hypothesis : \(P_{\alpha}[h_i \pmid b]\). The prior probability represents the weight of any important considerations not captured by the evidential likelihoods. Any relevant considerations that go beyond the evidence itself may be explicitly stated within expression \(b\) (in addition to whatever auxiliary hypotheses \(b\) may contain in support of the likelihoods). Thus, the prior probability of \(h_i\) may depend explicitly on the content of \(b\). It turns out that posterior probabilities depend only on the values of evidential likelihoods together with the values of prior probabilities.

As an illustration of the role of prior probabilities , consider the HIV test example described in the previous section. What the physician and the patient want to know is the value of the posterior probability, \(P_{\alpha}[h \pmid b\cdot c\cdot e]\), that the patient has HIV, \(h\), given the evidence of the positive test, \(c\cdot e\), and given the error rates of the test, described within \(b\). The value of this posterior probability depends on the likelihood (due to the error rates) of this patient obtaining a true-positive result, \(P[e \pmid h\cdot b\cdot c] = .99\), and of obtaining a false-positive result, \(P[e \pmid {\nsim}h\cdot b\cdot c] = .05\). In addition, the value of the of the posterior probability depends on how plausible it is that the patient has HIV prior to taking the test results into account, \(P_{\alpha}[h \pmid b]\). In the context of medical diagnosis, this prior probability is usually assessed on the basis of the base rate for HIV in the patient’s risk group (i.e., whether the patient is an IV drug user, has unprotected sex with multiple partners, etc.). On a rigorous approach to the logic, such information and its risk-relevance should be explicitly stated within the background information \(b\). To see the importance of this information, consider the following numerical results (which may be calculated using the formula called Bayes’ Theorem, presented in the next section). If the base rate for the patient’s risk group is relatively high, say \(P_{\alpha}[h \pmid b] = .10\), then the positive test result yields a posterior probability value for his having HIV of \(P_{\alpha}[h \pmid b\cdot c\cdot e] = .69\). However, if the patient is in a very low risk group, say \(P_{\alpha}[h \pmid b] = .001\), then a positive test result only raises the posterior probability of his having an HIV infection to \(P_{\alpha}[h \pmid b\cdot c\cdot e] = .02\). This posterior probability is much higher than the prior probability of .001, but should not worry the patient too much. This positive test result may well be due to the comparatively high false-positive rate for the test, rather than to the presence of HIV. This sort of test, with a false-positive rate as large as .05, is best used as a screening test; a positive result warrants conducting a second, more rigorous, less error-prone test.

More generally, in the evidential evaluation of scientific hypotheses and theories, prior probabilities represent assessments of non-evidential plausibility weightings among hypotheses. However, because the strengths of such plausibility assessments may vary among members of a scientific community, critics often brand such assessments as merely subjective , and take their role in Bayesian inference to be highly problematic. Bayesian inductivists counter that plausibility assessments play an important, legitimate role in the sciences, especially when evidence cannot suffice to distinguish among some alternative hypotheses. And, they argue, the epithet “merely subjective” is unwarranted. Such plausibility assessments are often backed by extensive arguments that may draw on forceful conceptual considerations.

Scientists often bring plausibility arguments to bear in assessing competing views. Although such arguments are seldom decisive, they may bring the scientific community into widely shared agreement, especially with regard to the implausibility of some logically possible alternatives. This seems to be the primary epistemic role of thought experiments. Consider, for example, the kinds of plausibility arguments that have been brought to bear on the various interpretations of quantum theory (e.g., those related to the measurement problem). These arguments go to the heart of conceptual issues that were central to the original development of the theory. Many of these issues were first raised by those scientists who made the greatest contributions to the development of quantum theory, in their attempts to get a conceptual hold on the theory and its implications.

Given any body of evidence, it is fairly easy to cook up a host of logically possible alternative hypotheses that make the evidence as probable as desired. In particular, it is easy to cook up hypotheses that logically entail any given body evidence, providing likelihood values equal to 1 for all the available evidence. Although most of these cooked up hypotheses will be laughably implausible, evidential likelihoods cannot rule them out. But, the only factors other than likelihoods that figure into the values of posterior probabilities for hypotheses are the values of their prior probabilities; so only prior probability assessments provide a place for the Bayesian logic to bring important plausibility considerations to bear. Thus, the Bayesian logic can only give implausible hypotheses their due via prior probability assessments.

It turns out that the mathematical structure of Bayesian inference makes prior probabilities especially well-suited to represent plausibility assessments among competing hypotheses. For, in the fully fleshed out account of evidential support for hypotheses (spelled out below), it will turn out that only ratios of prior probabilities for competing hypotheses, \(P_{\alpha}[h_j \pmid b] / P_{\alpha}[h_i \pmid b]\), together with ratios of likelihoods, \(P_{\alpha}[e \pmid h_j\cdot b\cdot c] / P_{\alpha}[e \pmid h_2\cdot b\cdot c]\), play essential roles. The ratio of prior probabilities is well-suited to represent how much more (or less) plausible hypothesis \(h_j\) is than competing hypothesis \(h_i\). Furthermore, the plausibility arguments on which such this comparative assessment is based may be explicitly stated within \(b\). So, given that an inductive logic needs to incorporate well-considered plausibility assessments (e.g. in order to lay low wildly implausible alternative hypotheses), the comparative assessment of Bayesian prior probabilities seems well-suited to do the job.

Thus, although prior probabilities may be subjective in the sense that agents may disagree on the relative strengths of plausibility arguments, the priors used in scientific contexts need not represent mere subjective whims . Rather, the comparative strengths of the priors for hypotheses should be supported by arguments about how much more plausible one hypothesis is than another. The important role of plausibility assessments is captured by such received bits of scientific wisdom as the well-known scientific aphorism, extraordinary claims require extraordinary evidence . That is, it takes especially strong evidence, in the form of extremely high values for (ratios of) likelihoods, to overcome the extremely low pre-evidential plausibility values possessed by some hypotheses. In the next section we’ll see precisely how this idea works, and we’ll return to it again in Section 3.4 .

When sufficiently strong evidence becomes available, it turns out that the contributions of prior plausibility assessments to the values of posterior probabilities may be substantially “washed out”, overridden by the evidence. That is, provided the prior probability of a true hypothesis isn’t assessed to be too close to zero, the influence of the values of the prior probabilities will very probably fade away as evidence accumulates. In Section 4 we’ll see precisely how this kind of Bayesian convergence to the true hypothesis works. Thus, it turns out that prior plausibility assessments play their most important role when the distinguishing evidence represented by the likelihoods remains weak.

One more point before moving on to the logic of Bayes’ Theorem. Some Bayesian logicists have maintained that posterior probabilities of hypotheses should be determined by syntactic logical form alone. The idea is that the likelihoods might reasonably be specified in terms of syntactic logical form; so if syntactic form might be made to determine the values of prior probabilities as well, then inductive logic would be fully “formal” in the same way that deductive logic is “formal”. Keynes and Carnap tried to implement this idea through syntactic versions of the principle of indifference—the idea that syntactically similar hypotheses should be assigned the same prior probability values. Carnap showed how to carry out this project in detail, but only for extremely simple formal languages. Most logicians now take the project to have failed because of a fatal flaw with the whole idea that reasonable prior probabilities can be made to depend on logical form alone. Semantic content should matter. Goodmanian grue-predicates provide one way to illustrate this point. [ 8 ] Furthermore, as suggested earlier, for this idea to apply to the evidential support of real scientific theories, scientists would have to assess the prior probabilities of each alternative theory based only on its syntactic structure. That seems an unreasonable way to proceed. Are we to evaluate the prior probabilities of alternative theories of gravitation, or for alternative quantum theories, by exploring only their syntactic structures, with absolutely no regard for their content—with no regard for what they say about the world? This seems an extremely dubious approach to the evaluation of real scientific theories. Logical structure alone cannot, and should not suffice for determining reasonable prior probability values for real scientific theories. Moreover, real scientific hypotheses and theories are inevitably subject to plausibility considerations based on what they say about the world. Prior probabilities are well-suited to represent the comparative weight of plausibility considerations for alternative hypotheses. But no reasonable assessment of comparative plausibility can derive solely from the logical form of hypotheses.

We will return to a discussion of prior probabilities a bit later. Let’s now see how Bayesian logic combines likelihoods with prior probabilities to yield posterior probabilities for hypotheses.

Any probabilistic inductive logic that draws on the usual rules of probability theory to represent how evidence supports hypotheses must be a Bayesian inductive logic in the broad sense. For, Bayes’ Theorem follows directly from the usual axioms of probability theory. Its importance derives from the relationship it expresses between hypotheses and evidence. It shows how evidence, via the likelihoods, combines with prior probabilities to produce posterior probabilities for hypotheses. We now examine several forms of Bayes’ Theorem, each derivable from axioms 1–5 .

The simplest version of Bayes’ Theorem as it applies to evidence for a hypothesis goes like this:

Bayes’ Theorem: Simple Form

This equation expresses the posterior probability of hypothesis \(h_i\) due to evidence \(e\), \(P_{\alpha}[h_i \pmid e]\), in terms of the likelihood of the evidence on that hypothesis, \(P_{\alpha}[e \pmid h_i]\), the prior probability of the hypothesis , \(P_{\alpha}[h_i]\), and the simple probability of the evidence , \(P_{\alpha}[e]\). The factor \(P_{\alpha}[e]\) is often called the expectedness of the evidence . Written this way, the theorem suppresses the experimental (or observational) conditions, \(c\), and all background information and auxiliary hypotheses, \(b\). As discussed earlier, both of these terms play an important role in logically connecting the hypothesis at issue, \(h_i\), to the evidence \(e\). In scientific contexts the objectivity of the likelihoods, \(P_{\alpha}[e \pmid h_i\cdot b \cdot c]\), almost always depends on such terms. So, although the suppression of experimental (or observational) conditions and auxiliary hypotheses is a common practice in accounts of Bayesian inference, the treatment below, and throughout the remainder of this article will make the role of these terms explicit.

The subscript \(\alpha\) on the evidential support function \(P_{\alpha}\) is there to remind us that more than one such function exists. A host of distinct probability functions satisfy axioms 1–5 , so each of them satisfies Bayes’ Theorem. Some of these probability functions may provide a better fit with our intuitive conception of how the evidential support for hypotheses should work. Nevertheless, there are bound to be reasonable differences among Bayesian agents regarding to the initial plausibility of a hypothesis \(h_i\). This diversity in initial plausibility assessments is represented by diverse values for prior probabilities for the hypothesis: \(P_{\alpha}[h_i]\), \(P_{\beta}[h_i]\), \(P_{\gamma}[h_i]\), etc. This usually results in diverse values for posterior probabilities for hypotheses: \(P_{\alpha}[h_i \pmid e]\), \(P_{\beta}[h_i \pmid e]\), \(P_{\gamma}[h_i \pmid e]\), etc. So it is important to keep the diversity among evidential support functions in mind.

Here is how the Simple Form of Bayes’ Theorem looks when terms for the experimental (or observational) conditions, \(c\), and the background information and auxiliary hypotheses \(b\) are made explicit:

Bayes’ Theorem: Simple Form with explicit Experimental Conditions, Background Information and Auxiliary Hypotheses

This version of the theorem determines the posterior probability of the hypothesis, \(P_{\alpha}[h_i \pmid b\cdot c\cdot e]\), from the value of the likelihood of the evidence according to that hypothesis (taken together with background and auxiliaries and the experimental conditions), \(P[e \pmid h_i\cdot b\cdot c]\), the value of the prior probability of the hypothesis (on background and auxiliaries), \(P_{\alpha}[h_i \pmid b]\), and the value of the expectedness of the evidence (on background and auxiliaries and the experimental conditions), \(P_{\alpha}[e \pmid b\cdot c]\). Notice that in the factor for the likelihood, \(P[e \pmid h_i\cdot b\cdot c]\), the subscript \(\alpha\) has been dropped. This marks the fact that in scientific contexts the likelihood of an evidential outcome \(e\) on the hypothesis together with explicit background and auxiliary hypotheses and the description of the experimental conditions, \(h_i\cdot b\cdot c\), is usually objectively determinate. This factor represents what the hypothesis (in conjunction with background and auxiliaries) objectively says about the likelihood of possible evidential outcomes of the experimental conditions. So, all reasonable support functions should agree on the values for likelihoods. (Section 5 will treat cases where the likelihoods may lack this kind of objectivity.)

This version of Bayes’ Theorem includes a term that represents the ratio of the likelihood of the experimental conditions on the hypothesis and background information (and auxiliaries) to the “likelihood” of the experimental conditions on the background (and auxiliaries) alone: \(P_{\alpha}[c \pmid h_i\cdot b]/ P_{\alpha}[c \pmid b]\). Arguably the value of this term should be 1, or very nearly 1, since the truth of the hypothesis at issue should not significantly affect how likely it is that the experimental conditions are satisfied. If various alternative hypotheses assign significantly different likelihoods to the experimental conditions themselves, then such conditions should more properly be included as part of the evidential outcome \(e\).

Both the prior probability of the hypothesis and the expectedness tend to be somewhat subjective factors in that various agents from the same scientific community may legitimately disagree on what values these factors should take. Bayesian logicians usually accept the apparent subjectivity of the prior probabilities of hypotheses, but find the subjectivity of the expectedness to be more troubling. This is due at least in part to the fact that in a Bayesian logic of evidential support the value of the expectedness cannot be determined independently of likelihoods and prior probabilities of hypotheses. That is, when, for each member of a collection of alternative hypotheses, the likelihood \(P[e \pmid h_j\cdot b\cdot c]\) has an objective (or intersubjectively agreed) value, the expectedness is constrained by the following equation (where the sum ranges over a mutually exclusive and exhaustive collection of alternative hypotheses \(\{h_1, h_2 , \ldots ,h_m , \ldots \}\), which may be finite or countably infinite):

This equation shows that the values for the prior probabilities together with the values of the likelihoods uniquely determine the value for the expectedness of the evidence . Furthermore, it implies that the value of the expectedness must lie between the largest and smallest of the various likelihood values implied by the alternative hypotheses. However, the precise value of the expectedness can only be calculated this way when every alternative to hypothesis \(h_j\) is specified. In cases where some alternative hypotheses remain unspecified (or undiscovered), the value of the expectedness is constrained in principle by the totality of possible alternative hypotheses, but there is no way to figure out precisely what its value should be.

Troubles with determining a numerical value for the expectedness of the evidence may be circumvented by appealing to another form of Bayes’ Theorem, a ratio form that compares hypotheses one pair at a time:

Bayes’ Theorem: Ratio Form

The clause \(P_{\alpha}[c \pmid h_j\cdot b] = P_{\alpha}[c \pmid h_i\cdot b]\) says that the experimental (or observation) condition described by \(c\) is as likely on \((h_i\cdot b)\) as on \((h_j\cdot b)\) — i.e., the experimental or observation conditions are no more likely according to one hypothesis than according to the other. [ 9 ]

This Ratio Form of Bayes’ Theorem expresses how much more plausible, on the evidence, one hypothesis is than another. Notice that the likelihood ratios carry the full import of the evidence. The evidence influences the evaluation of hypotheses in no other way. The only other factor that influences the value of the ratio of posterior probabilities is the ratio of the prior probabilities. When the likelihoods are fully objective, any subjectivity that affects the ratio of posteriors can only arise via subjectivity in the ratio of the priors.

This version of Bayes’s Theorem shows that in order to evaluate the posterior probability ratios for pairs of hypotheses, the prior probabilities of hypotheses need not be evaluated absolutely; only their ratios are needed. That is, with regard to the priors, the Bayesian evaluation of hypotheses only relies on how much more plausible one hypothesis is than another (due to considerations expressed within b ). This kind of Bayesian evaluation of hypotheses is essentially comparative in that only ratios of likelihoods and ratios of prior probabilities are ever really needed for the assessment of scientific hypotheses. Furthermore, we will soon see that the absolute values of the posterior probabilities of hypotheses entirely derive from the posterior probability ratios provided by the Ratio Form of Bayes’ Theorem.

When the evidence consists of a collection of n distinct experiments or observations, we may explicitly represent this fact by replacing the term ‘\(c\)’ by the conjunction of experimental or observational conditions, \((c_1\cdot c_2\cdot \ldots \cdot c_n)\), and replacing the term ‘\(e\)’ by the conjunction of their respective outcomes, \((e_1\cdot e_2\cdot \ldots \cdot e_n)\). For notational convenience, let’s use the term ‘\(c^n\)’ to abbreviate the conjunction of n the experimental conditions, and we use the term ‘\(e^n\)’ to abbreviate the corresponding conjunction of n their respective outcomes. Relative to any given hypothesis \(h\), the evidential outcomes of distinct experiments or observations will usually be probabilistically independent of one another, and also independent of the experimental conditions for one another. In that case we have:

When the Ratio Form of Bayes’ Theorem is extended to explicitly represent the evidence as consisting of a collection of n of distinct experiments (or observations) and their respective outcomes, it takes the following form.

Bayes’ Theorem: Ratio Form for a Collection of n Distinct Evidence Claims

Furthermore, when evidence claims are probabilistically independent of one another, we have

Let’s consider a simple example of how the Ratio Form of Bayes’ Theorem applies to a collection of independent evidential events. Suppose we possess a warped coin and want to determine its propensity for heads when tossed in the usual way. Consider two hypotheses, \(h_{[p]}\) and \(h_{[q]}\), which say that the propensities for the coin to come up heads on the usual kinds of tosses are \(p\) and \(q\), respectively. Let \(c^n\) report that the coin is tossed n times in the normal way, and let \(e^n\) report that precisely m occurrences of heads has resulted. Supposing that the outcomes of such tosses are probabilistically independent (asserted by \(b\)), the respective likelihoods take the binomial form

with \(r\) standing in for \(p\) and for \(q\), respectively. Then, Equation 9** yields the following formula, where the likelihood ratio is the ratio of the respective binomial terms:

When, for instance, the coin is tossed \(n = 100\) times and comes up heads \(m = 72\) times, the evidence for hypothesis \(h_{[1/2]}\) as compared to \(h_{[3/4]}\) is given by the likelihood ratio

In that case, even if the prior plausibility considerations (expressed within \(b\)) make it 100 times more plausible that the coin is fair than that it is warped towards heads with propensity 3/4 — i.e., even if \(P_{\alpha}[h_{[1/2]} \pmid b] / P_{\alpha}[h_{[3/4]} \pmid b] = 100\) — the evidence provided by these tosses makes the posterior plausibility that the coin is fair only about 6/1000 ths as plausible as the hypothesis that it is warped towards heads with propensity 3/4 :

Thus, such evidence strongly refutes the “fairness hypothesis” relative to the “3/4- heads hypothesis”, provided the assessment of prior prior plausibilities doesn’t make the latter hypothesis too extremely implausible to begin with. Notice, however, that strong refutation is not absolute refutation . Additional evidence could reverse this trend towards the refutation of the fairness hypothesis .

This example employs repetitions of the same kind of experiment—repeated tosses of a coin. But the point holds more generally. If, as the evidence increases, the likelihood ratios

approach 0, then the Ratio Forms of Bayes’ Theorem, Equations \(9*)\) and \(9**)\), show that the posterior probability of \(h_j\) must approach 0 as well, since

Such evidence comes to strongly refute \(h_j\), with little regard for its prior plausibility value. Indeed, Bayesian induction turns out to be a version of eliminative induction , and Equation \(9*\) and \(9**\) begin to illustrate this. For, suppose that \(h_i\) is the true hypothesis, and consider what happens to each of its false competitors, \(h_j\). If enough evidence becomes available to drive each of the likelihood ratios

toward 0 (as n increases), then Equation \(9*\) says that each false \(h_j\) will become effectively refuted — each of their posterior probabilities will approaches 0 (as n increases). As a result, the posterior probability of \(h_i\) must approach 1. The next two equations show precisely how this works.

If we sum the ratio versions of Bayes’ Theorem in Equation \(9*\) over all alternatives to hypothesis \(h_i\) (including the catch-all alternative \(h_K\), if appropriate), we get the Odds Form of Bayes’ Theorem. By definition, the odds against a statement \(A\) given \(B\) is related to the probability of \(A\) given \(B\) as follows:

This notion of odds gives rise to the following version of Bayes’ Theorem:

Bayes’ Theorem: Odds Form

where the factor following the ‘ + ’ sign is only required in cases where a catch-all alternative hypothesis, \(h_K\), is needed.

Recall that when we have a finite collection of concrete alternative hypotheses available, \(\{h_1, h_2 , \ldots ,h_m\}\), but where this set of alternatives is not exhaustive (where additional, unarticulated, undiscovered alternative hypotheses may exist), the catch-all alternative hypothesis \(h_K\) is just the denial of each of the concrete alternatives, \(({\nsim}h_1\cdot{\nsim}h_2\cdot \ldots \cdot{\nsim}h_m)\). Generally, the likelihood of evidence claims relative to a catch-all hypothesis will not enjoy the same kind of objectivity possessed by the likelihoods for concrete alternative hypotheses. So, we leave the subscript \(\alpha\) attached to the likelihood for the catch-all hypothesis to indicate this lack of objectivity.

Although the catch-all hypothesis may lack objective likelihoods, the influence of the catch-all term in Bayes’ Theorem diminishes as additional concrete hypotheses are articulated. That is, as new hypotheses are discovered they are “peeled off” of the catch-all. So, when a new hypothesis \(h_{m+1}\) is formulated and made explicit, the old catch-all hypothesis \(h_K\) is replaced by a new catch-all, \(h_{K*}\), of form \(({\nsim}h_1\cdot \cdot{\nsim}h_2\cdot \ldots \cdot{\nsim}h_{m}\cdot{\nsim}h_{m+1})\); and the prior probability for the new catch-all hypothesis is gotten by diminishing the prior of the old catch-all: \(P_{\alpha}[h_{K*} \pmid b] = P_{\alpha}[h_K \pmid b] - P_{\alpha}[h_{m+1} \pmid b]\). Thus, the influence of the catch-all term should diminish towards 0 as new alternative hypotheses are made explicit. [ 10 ]

If increasing evidence drives towards 0 the likelihood ratios comparing each competitor \(h_j\) with hypothesis \(h_i\), then the odds against \(h_i\), \(\Omega_{\alpha}[{\nsim}h_i \pmid b\cdot c^{n}\cdot e^{n}]\), will approach 0 (provided that priors of catch-all terms, if needed, approach 0 as well, as new alternative hypotheses are made explicit and peeled off). And, as \(\Omega_{\alpha}[{\nsim}h_i \pmid b\cdot c^{n}\cdot e^{n}]\) approaches 0, the posterior probability of \(h_i\) goes to 1. This derives from the fact that the odds against \(h_i\) is related to and its posterior probability by the following formula:

Bayes’ Theorem: General Probabilistic Form

The odds against a hypothesis depends only on the values of ratios of posterior probabilities , which entirely derive from the Ratio Form of Bayes’ Theorem. Thus, we see that the individual value of the posterior probability of a hypothesis depends only on the ratios of posterior probabilities , which come from the Ratio Form of Bayes’ Theorem. Thus, the Ratio Form of Bayes’ Theorem captures all the essential features of the Bayesian evaluation of hypothesis. It shows how the impact of evidence (in the form of likelihood ratios) combines with comparative plausibility assessments of hypotheses (in the form of ratios of prior probabilities) to provide a net assessment of the extent to which hypotheses are refuted or supported via contests with their rivals.

There is a result, a kind of Bayesian Convergence Theorem , that shows that if \(h_i\) (together with \(b\cdot c^n)\) is true, then the likelihood ratios

comparing evidentially distinguishable alternative hypothesis \(h_j\) to \(h_i\) will very probably approach 0 as evidence accumulates (i.e., as n increases). Let’s call this result the Likelihood Ratio Convergence Theorem . When this theorem applies, Equation \(9^*\) shows that the posterior probability of a false competitor \(h_j\) will very probably approach 0 as evidence accumulates, regardless of the value of its prior probability \(P_{\alpha}[h_j \pmid b]\). As this happens to each of \(h_i\)’s false competitors, Equations 10 and 11 say that the posterior probability of the true hypothesis, \(h_i\), will approach 1 as evidence increases. [ 11 ] Thus, Bayesian induction is at bottom a version of induction by elimination , where the elimination of alternatives comes by way of likelihood ratios approaching 0 as evidence accumulates. Thus, when the Likelihood Ratio Convergence Theorem applies, the Criterion of Adequacy for an Inductive Logic described at the beginning of this article will be satisfied: As evidence accumulates, the degree to which the collection of true evidence statements comes to support a hypothesis, as measured by the logic, should very probably come to indicate that false hypotheses are probably false and that true hypotheses are probably true. We will examine this Likelihood Ratio Convergence Theorem in Section 4 . [ 12 ]

A view called Likelihoodism relies on likelihood ratios in much the same way as the Bayesian logic articulated above. However, Likelihoodism attempts to avoid the use of prior probabilities. For an account of this alternative view, see the supplement Likelihood Ratios, Likelihoodism, and the Law of Likelihood . For more discussion of Bayes’ Theorem and its application, see the entries on Bayes’ Theorem and on Bayesian Epistemology in this Encyclopedia .

Given that a scientific community should largely agree on the values of the likelihoods, any significant disagreement among them with regard to the values of posterior probabilities of hypotheses should derive from disagreements over their assessments of values for the prior probabilities of those hypotheses. We saw in Section 3.3 that the Bayesian logic of evidential support need only rely on assessments of ratios of prior probabilities —on how much more plausible one hypothesis is than another. Thus, the logic of evidential support only requires that scientists can assess the comparative plausibilities of various hypotheses. Presumably, in scientific contexts the comparative plausibility values for hypotheses should depend on explicit plausibility arguments, not merely on privately held opinions. (Formally, the logic may represent comparative plausibility arguments by explicit statements expressed within \(b\).) It would be highly unscientific for a member of the scientific community to disregard or dismiss a hypothesis that other members take to be a reasonable proposal with only the comment, “don’t ask me to give my reasons, it’s just my opinion”. Even so, agents may be unable to specify precisely how much more strongly the available plausibility arguments support a hypothesis over an alternative; so prior probability ratios for hypotheses may be vague. Furthermore, agents in a scientific community may disagree about how strongly the available plausibility arguments support a hypothesis over a rival hypothesis; so prior probability ratios may be somewhat diverse as well.

Both the vagueness of comparative plausibilities assessments for individual agents and the diversity of such assessments among the community of agents can be represented formally by sets of support functions, \(\{P_{\alpha}, P_{\beta}, \ldots \}\), that agree on the values for the likelihoods but encompass a range of values for the (ratios of) prior probabilities of hypotheses. Vagueness and diversity are somewhat different issues, but they may be represented in much the same way. Let’s briefly consider each in turn.

Assessments of the prior plausibilities of hypotheses will often be vague—not subject to the kind of precise quantitative treatment that a Bayesian version of probabilistic inductive logic may seem to require for prior probabilities. So, it may seem that the kind of assessment of prior probabilities required to get the Bayesian algorithm going cannot be accomplished in practice. To see how Bayesian inductivists address this worry, first recall the Ratio Form of Bayes’ Theorem, Equation \(9^*\).

Recall that this Ratio Form of the theorem captures the essential features of the logic of evidential support, even though it only provides a value for the ratio of the posterior probabilities. Notice that the ratio form of the theorem easily accommodates situations where we don’t have precise numerical values for prior probabilities. It only depends on our ability to assess how much more or less plausible alternative hypothesis \(h_j\) is than hypothesis \(h_i\)—only the value of the ratio \(P_{\alpha}[h_j \pmid b] / P_{\alpha}[h_i \pmid b]\) need be assessed; the values of the individual prior probabilities are not needed. Such comparative plausibilities are much easier to assess than specific numerical values for the prior probabilities of individual hypotheses. When combined with the ratio of likelihoods , this ratio of priors suffices to yield an assessment of the ratio of posterior plausibilities ,

Although such posterior ratios don’t supply values for the posterior probabilities of individual hypotheses, they place a crucial constraint on the posterior support of hypothesis \(h_j\), since

This Ratio Form of Bayes’ Theorem tolerates a good deal of vagueness or imprecision in assessments of the ratios of prior probabilities. In practice one need only assess bounds for these prior plausibility ratios to achieve meaningful results. Given a prior ratio in a specific interval,

a likelihood ratio

results in a posterior support ratio in the interval

(Technically each probabilistic support function assigns a specific numerical value to each pair of sentences; so when we write an inequality like

we are really referring to a set of probability functions \(P_{\alpha}\), a vagueness set , for which the inequality holds. Thus, technically, the Bayesian logic employs sets of probabilistic support functions to represent the vagueness in comparative plausibility values for hypotheses.)

Observe that if the likelihood ratio values \(\LR^n\) approach 0 as the amount of evidence \(e^n\) increases, the interval of values for the posterior probability ratio must become tighter as the upper bound (\(\LR^n\times r)\) approaches 0. Furthermore, the absolute degree of support for \(h_j\), \(P_{\alpha}[h_j \pmid b\cdot c^{n}\cdot e^{n}]\), must also approach 0.

This observation is really useful. For, it can be shown that when \(h_{i}\cdot b\cdot c^{n}\) is true and \(h_j\) is empirically distinct from \(h_i\), the continual pursuit of evidence is very likely to result in evidential outcomes \(e^n\) that (as n increases) yield values of likelihood ratios \(P[e^n \pmid h_{j}\cdot b\cdot c^{n}] / P[e^n \pmid h_{i}\cdot b\cdot c^{n}]\) that approach 0 as the amount of evidence increases. This result, called the Likelihood Ratio Convergence Theorem , will be investigated in more detail in Section 4 . When that kind of convergence towards 0 for likelihood ratios occurs, the upper bound on the posterior probability ratio also approaches 0, driving the posterior probability of \(h_j\) to approach 0 as well, effectively refuting hypothesis \(h_j\). Thus, false competitors of a true hypothesis will effectively be eliminated by increasing evidence. As this happens, Equations 9* through 11 show that the posterior probability \(P_{\alpha}[h_i \pmid b\cdot c^{n}\cdot e^{n}]\) of the true hypothesis \(h_i\) approaches 1.

Thus, Bayesian logic of inductive support for hypotheses is a form of eliminative induction, where the evidence effectively refutes false alternatives to the true hypothesis. Because of its eliminative nature, the Bayesian logic of evidential support doesn’t require precise values for prior probabilities. It only needs to draw on bounds on the values of comparative plausibility ratios, and these bounds only play a significant role while evidence remains fairly weak. If the true hypothesis is assessed to be comparatively plausible (due to plausibility arguments contained in b ), then plausibility assessments give it a leg-up over alternatives. If the true hypothesis is assessed to be comparatively implausible, the plausibility assessments merely slow down the rate at which it comes to dominate its rivals, reflecting the idea that extraordinary hypotheses require extraordinary evidence (or an extraordinary accumulation of evidence) to overcome their initial implausibilities. Thus, as evidence accumulates, the agent’s vague initial plausibility assessments transform into quite sharp posterior probabilities that indicate their strong refutation or support by the evidence.

When the various agents in a community may widely disagree over the non-evidential plausibilities of hypotheses, the Bayesian logic of evidential support may represent this kind of diversity across the community of agents as a collection of the agents’ vagueness sets of support functions. Let’s call such a collection of support functions a diversity set . That is, a diversity set is just a set of support functions \(P_{\alpha}\) that cover the ranges of values for comparative plausibility assessments for pairs of competing hypotheses

as assessed by the scientific community. But, once again, if accumulating evidence drives the likelihood ratios comparing various alternative hypotheses to the true hypothesis towards 0, the range of support functions in a diversity set will come to near agreement, near 0, on the values for posterior probabilities of false competitors of the true hypothesis. So, not only does such evidence firm up each agent’s vague initial plausibility assessment, it also brings the whole community into agreement on the near refutation of empirically distinct competitors of a true hypothesis. As this happens, the posterior probability of the true hypothesis may approach 1. The Likelihood Ratio Convergence Theorem implies that this kind of convergence to the truth should very probably happen, provided that the true hypothesis is empirically distinct enough from its rivals.

One more point about prior probabilities and Bayesian convergence should be mentioned before proceeding to Section 4 . Some subjectivist versions of Bayesian induction seem to suggest that an agent’s prior plausibility assessments for hypotheses should stay fixed once-and-for-all, and that all plausibility updating should be brought about via the likelihoods in accord with Bayes’ Theorem. Critics argue that this is unreasonable. The members of a scientific community may quite legitimately revise their (comparative) prior plausibility assessments for hypotheses from time to time as they rethink plausibility arguments and bring new considerations to bear. This seems a natural part of the conceptual development of a science. It turns out that such reassessments of the comparative plausibilities of hypotheses poses no difficulty for the probabilistic inductive logic discussed here. Such reassessments may be represented by the addition or modification of explicit statements that modify the background information b . Such reassessments may result in (non-Bayesian) transitions to new vagueness sets for individual agents and new diversity sets for the community. The logic of Bayesian induction (as described here) has nothing to say about what values the prior plausibility assessments for hypotheses should have; and it places no restrictions on how they might change over time. Provided that the series of reassessments of (comparative) prior plausibilities doesn’t happen to diminish the (comparative) prior plausibility value of the true hypothesis towards zero (or, at least, doesn’t do so too quickly), the Likelihood Ratio Convergence Theorem implies that the evidence will very probably bring the posterior probabilities of empirically distinct rivals of the true hypothesis to approach 0 via decreasing likelihood ratios; and as this happens, the posterior probability of the true hypothesis will head towards 1.

(Those interested in a Bayesian account of Enumerative Induction and the estimation of values for relative frequencies of attributes in populations should see the supplement, Enumerative Inductions: Bayesian Estimation and Convergence .)

4. The Likelihood Ratio Convergence Theorem

In this section we will investigate the Likelihood Ratio Convergence Theorem . This theorem shows that under certain reasonable conditions, when hypothesis \(h_i\) (in conjunction with auxiliaries in b ) is true and an alternative hypothesis \(h_j\) is empirically distinct from \(h_i\) on some possible outcomes of experiments or observations described by conditions \(c_k\), then it is very likely that a long enough sequence of such experiments and observations c\(^n\) will produce a sequence of outcomes \(e^n\) that yields likelihood ratios \(P[e^n \pmid h_{j}\cdot b\cdot c^{n}] / P[e^n \pmid h_{i}\cdot b\cdot c^{n}]\) that approach 0, favoring \(h_i\) over \(h_j\), as evidence accumulates (i.e., as n increases). This theorem places an explicit lower bound on the “rate of probable convergence” of these likelihood ratios towards 0. That is, it puts a lower bound on how likely it is, if \(h_i\) is true, that a stream of outcomes will occur that yields likelihood ratio values against \(h_j\) as compared to \(h_i\) that lie within any specified small distance above 0.

The theorem itself does not require the full apparatus of Bayesian probability functions. It draws only on likelihoods. Neither the statement of the theorem nor its proof employ prior probabilities of any kind. So even likelihoodists , who eschew the use of Bayesian prior probabilities, may embrace this result. Given the forms of Bayes’ Theorem, 9*-11 from the previous section, the Likelihood Ratio Convergence Theorem further implies the likely convergence to 0 of the posterior probabilities of false competitors of a true hypothesis. That is, when the ratios \(P[e^n \pmid h_{j}\cdot b\cdot c^{n}] / P[e^n \pmid h_{i}\cdot b\cdot c^{n}]\) approach 0 for increasing n , the Ratio Form of Bayes’ Theorem, Equation 9* , says that the posterior probability of \(h_j\) must also approach 0 as evidence accumulates, regardless of the value of its prior probability. So, support functions in collections representing vague prior plausibilities for an individual agent (i.e., a vagueness set) and representing the diverse range of priors for a community of agents (i.e., a diversity set) will come to agree on the near 0 posterior probability of empirically distinct false rivals of a true hypothesis. And as the posterior probabilities of false competitors fall, the posterior probability of the true hypothesis heads towards 1. Thus, the theorem establishes that the inductive logic of probabilistic support functions satisfies the Criterion of Adequacy (CoA) suggested at the beginning of this article.

The Likelihood Ratio Convergence Theorem merely provides some sufficient conditions for probable convergence. But likelihood ratios may well converge towards 0 (in the way described by the theorem) even when the antecedent conditions of the theorem are not satisfied. This theorem overcomes many of the objections raised by critics of Bayesian convergence results. First, this theorem does not employ second-order probabilities ; it says noting about the probability of a probability. It only concerns the probability of a particular disjunctive sentence that expresses a disjunction of various possible sequences of experimental or observational outcomes. The theorem does not require evidence to consist of sequences of events that, according to the hypothesis, are identically distributed (like repeated tosses of a die). The result is most easily expressed in cases where the individual outcomes of a sequence of experiments or observations are probabilistically independent, given each hypothesis. So that is the version that will be presented in this section. However, a version of the theorem also holds when the individual outcomes of the evidence stream are not probabilistically independent, given the hypotheses. (This more general version of the theorem will be presented in a supplement on the Probabilistic Refutation Theorem , below, where the proof of both versions is provided.) In addition, this result does not rely on supposing that the probability functions involved are countably additive . Furthermore, the explicit lower bounds on the rate of convergence provided by this result means that there is no need to wait for the infinitely long run before convergence occurs (as some critics seem to think).

It is sometimes claimed that Bayesian convergence results only work when an agent locks in values for the prior probabilities of hypotheses once-and-for-all, and then updates posterior probabilities from there only by conditioning on evidence via Bayes Theorem. The Likelihood Ratio Convergence Theorem , however, applies even if agents revise their prior probability assessments over time. Such non-Bayesian shifts from one support function (or vagueness set) to another may arise from new plausibility arguments or from reassessments of the strengths of old ones. The Likelihood Ratio Convergence Theorem itself only involves the values of likelihoods. So, provided such reassessments don’t push the prior probability of the true hypothesis towards 0 too rapidly , the theorem implies that the posterior probabilities of each empirically distinct false competitor will very probably approach 0 as evidence increases. [ 13 ]

To specify the details of the Likelihood Ratio Convergence Theorem we’ll need a few additional notational conventions and definitions. Here they are.

For a given sequence of n experiments or observations \(c^n\), consider the set of those possible sequences of outcomes that would result in likelihood ratios for \(h_j\) over \(h_i\) that are less than some chosen small number \(\varepsilon \gt 0\). This set is represented by the expression,

Placing the disjunction symbol ‘\(\vee\)’ in front of this expression yields an expression,

that we’ll use to represent the disjunction of all outcome sequences \(e^n\) in this set. So,

is just a particular sentence that says, in effect, “one of the sequences of outcomes of the first n experiments or observations will occur that makes the likelihood ratio for \(h_j\) over \(h_i\) less than \(\varepsilon\)”.

The Likelihood Ratio Convergence Theorem says that under certain conditions (covered in detail below), the likelihood of a disjunctive sentence of this sort, given that ‘\(h_{i}\cdot b\cdot c^{n}\)’ is true,

must be at least \(1-(\psi /n)\), for some explicitly calculable term \(\psi\). Thus, the true hypothesis \(h_i\) probabilistically implies that as the amount of evidence, n , increases, it becomes highly likely (as close to 1 as you please) that one of the outcome sequences \(e^n\) will occur that yields a likelihood ratio \(P[e^n \pmid h_{j}\cdot b\cdot c^{n}] / P[e^n \pmid h_{i}\cdot b\cdot c^{n}]\) less than \(\varepsilon\); and this holds for any specific value of \(\varepsilon\) you may choose. As this happens, the posterior probability of \(h_i\)’s false competitor, \(h_j\), must approach 0, as required by the Ratio Form of Bayes’ Theorem, Equation 9* .

The term \(\psi\) in the lower bound of this probability depends on a measure of the empirical distinctness of the two hypotheses \(h_j\) and \(h_i\) for the proposed sequence of experiments and observations \(c^n\). To specify this measure we need to contemplate the collection of possible outcomes of each experiment or observation. So, consider some sequence of experimental or observational conditions described by sentences \(c_1,c_2 ,\ldots ,c_n\). Corresponding to each condition \(c_k\) there will be some range of possible alternative outcomes. Let \(O_{k} = \{o_{k1},o_{k2},\ldots ,o_{kw}\}\) be a set of statements describing the alternative possible outcomes for condition \(c_k\). (The number of alternative outcomes will usually differ for distinct experiments among those in the sequence \(c_1 ,\ldots ,c_n\); so, the value of w may depend on \(c_k\).) For each hypothesis \(h_j\), the alternative outcomes of \(c_k\) in \(O_k\) are mutually exclusive and exhaustive, so we have:

We now let expressions of form ‘\(e_k\)’ act as variables that range over the possible outcomes of condition \(c_k\)—i.e., \(e_k\) ranges over the members of \(O_k\). As before, ‘\(c^n\)’ denotes the conjunction of the first n test conditions, \((c_1\cdot c_2\cdot \ldots \cdot c_n)\), and ‘\(e^n\)’ represents possible sequences of corresponding outcomes, \((e_1\cdot e_2\cdot \ldots \cdot e_n)\). Let’s use the expression ‘ E\(^n\) ’ to represent the set of all possible outcome sequences that may result from the sequence of conditions c\(^n\) . So, for each hypothesis \(h_j\) (including \(h_i)\), \(\sum_{e^n\in E^n} P[e^n \pmid h_{j}\cdot b\cdot c^{n}] = 1\).

Everything introduced in this subsection is mere notational convention. No substantive suppositions (other than the axioms of probability theory) have yet been introduced. The version of the Likelihood Ratio Convergence Theorem I’ll present below does, however, draw on one substantive supposition, although a rather weak one. The next subsection will discuss that supposition in detail.

In most scientific contexts the outcomes in a stream of experiments or observations are probabilistically independent of one another relative to each hypothesis under consideration, or can at least be divided up into probabilistically independent parts. For our purposes probabilistic independence of evidential outcomes on a hypothesis divides neatly into two types.

Definition: Independent Evidence Conditions :

• A sequence of outcomes \(e^k\) is condition-independent of a condition for an additional experiment or observation \(c_{k+1}\), given \(h\cdot b\) together with its own conditions \(c^k\), if and only if \[ P[e^k \pmid h\cdot b\cdot c^{k }\cdot c_{ k+1}] = P[e^k \pmid h\cdot b\cdot c^k] . \]
• An individual outcome \(e_k\) is result-independent of a sequence of other observations and their outcomes \((c^{k-1}\cdot e^{k-1})\), given \(h\cdot b\) and its own condition \(c_k\), if and only if \[ P[e_k \pmid h\cdot b\cdot c_k\cdot(c^{k-1 }\cdot e^{ k-1})] = P[e_k \pmid h\cdot b\cdot c_k] . \]

When these two conditions hold, the likelihood for an evidence sequence may be decomposed into the product of the likelihoods for individual experiments or observations. To see how the two independence conditions affect the decomposition, first consider the following formula, which holds even when neither independence condition is satisfied:

When condition-independence holds, the likelihood of the whole evidence stream parses into a product of likelihoods that probabilistically depend on only past observation conditions and their outcomes. They do not depend on the conditions for other experiments whose outcomes are not yet specified. Here is the formula:

Finally, whenever both independence conditions are satisfied we have the following relationship between the likelihood of the evidence stream and the likelihoods of individual experiments or observations:

(For proofs of Equations 12–14 see the supplement Immediate Consequences of Independent Evidence Conditions .)

In scientific contexts the evidence can almost always be divided into parts that satisfy both clauses of the Independent Evidence Condition with respect to each alternative hypothesis. To see why, let us consider each independence condition more carefully.

Condition-independence says that the mere addition of a new observation condition \(c_{k+1}\), without specifying one of its outcomes , does not alter the likelihood of the outcomes \(e^k\) of other experiments \(c^k\). To appreciate the significance of this condition, imagine what it would be like if it were violated. Suppose hypothesis \(h_j\) is some statistical theory, say, for example, a quantum theory of superconductivity. The conditions expressed in \(c^k\) describe a number of experimental setups, perhaps conducted in numerous labs throughout the world, that test a variety of aspects of the theory (e.g., experiments that test electrical conductivity in different materials at a range of temperatures). An outcome sequence \(e^k\) describes the results of these experiments. The violation of condition-independence would mean that merely adding to \(h_{j}\cdot b\cdot c^{k}\) a statement \(c_{k+1}\) describing how an additional experiment has been set up, but with no mention of its outcome, changes how likely the evidence sequence \(e^k\) is taken to be. What \((h_j\cdot b)\) says via likelihoods about the outcomes \(e^k\) of experiments \(c^k\) differs as a result of merely supplying a description of another experimental arrangement, \(c_{k+1}\). Condition-independence , when it holds, rules out such strange effects.

Result-independence says that the description of previous test conditions together with their outcomes is irrelevant to the likelihoods of outcomes for additional experiments. If this condition were widely violated, then in order to specify the most informed likelihoods for a given hypothesis one would need to include information about volumes of past observations and their outcomes. What a hypothesis says about future cases would depend on how past cases have gone. Such dependence had better not happen on a large scale. Otherwise, the hypothesis would be fairly useless, since its empirical import in each specific case would depend on taking into account volumes of past observational and experimental results. However, even if such dependencies occur, provided they are not too pervasive, result-independence can be accommodated rather easily by packaging each collection of result-dependent data together, treating it like a single extended experiment or observation. The result-independence condition will then be satisfied by letting each term ‘\(c_k\)’ in the statement of the independence condition represent a conjunction of test conditions for a collection of result-dependent tests, and by letting each term ‘\(e_k\)’ (and each term ‘\(o_{ku}\)’) stand for a conjunction of the corresponding result-dependent outcomes. Thus, by packaging result-dependent data together in this way, the result-independence condition is satisfied by those (conjunctive) statements that describe the separate, result-independent chunks. [ 14 ]

The version of the Likelihood Ratio Convergence Theorem we will examine depends only on the Independent Evidence Conditions (together with the axioms of probability theory). It draws on no other assumptions. Indeed, an even more general version of the theorem can be established, a version that draws on neither of the Independent Evidence Conditions . However, the Independent Evidence Conditions will be satisfied in almost all scientific contexts, so little will be lost by assuming them. (And the presentation will run more smoothly if we side-step the added complications needed to explain the more general result.)

From this point on, let us assume that the following versions of the Independent Evidence Conditions hold.

Assumption: Independent Evidence Assumptions . For each hypothesis h and background b under consideration, we assume that the experiments and observations can be packaged into condition statements, \(c_1 ,\ldots ,c_k, c_{k+1},\ldots\), and possible outcomes in a way that satisfies the following conditions:

• Each sequence of possible outcomes \(e^k\) of a sequence of conditions \(c^k\) is condition-independent of additional conditions \(c_{k+1}\)—i.e., \[P[e^k \pmid h\cdot b\cdot c^{k}\cdot c_{k+1}] = P[e^k \pmid h\cdot b\cdot c^k].\]
• Each possible outcome \(e_k\) of condition \(c_k\) is result-independent of sequences of other observations and possible outcomes \((c^{k-1}\cdot e^{k-1})\)—i.e., \[P[e_k \pmid h\cdot b\cdot c_k\cdot(c^{k-1}\cdot e^{k-1})] = P[e_k \pmid h\cdot b\cdot c_k].\]

We now have all that is needed to begin to state the Likelihood Ratio Convergence Theorem .

The Likelihood Ratio Convergence Theorem comes in two parts. The first part applies only to those experiments or observations \(c_k\) within the total evidence stream \(c^n\) for which some of the possible outcomes have 0 likelihood of occurring according to hypothesis \(h_j\) but have non-0 likelihood of occurring according to \(h_i\). Such outcomes are highly desirable. If they occur, the likelihood ratio comparing \(h_j\) to \(h_i\) will become 0, and \(h_j\) will be falsified . So-called crucial experiments are a special case of this, where for at least one possible outcome \(o_{ku}\), \(P[o_{ku} \pmid h_{i}\cdot b\cdot c_{k}] = 1\) and \(P[o_{ku} \pmid h_{j}\cdot b\cdot c_{k}] = 0\). In the more general case \(h_i\) together with b says that one of the outcomes of \(c_k\) is at least minimally probable, whereas \(h_j\) says that this outcome is impossible—i.e., \(P[o_{ku} \pmid h_{i}\cdot b\cdot c_{k}] \gt 0\) and \(P[o_{ku} \pmid h_{j}\cdot b\cdot c_{k}] = 0\). It will be convenient to define a term for this situation.

Definition: Full Outcome Compatibility. Let’s call \(h_j\) fully outcome-compatible with \(h_i\) on experiment or observation \(c_k\) just when , for each of its possible outcomes \(e_k\), if \(P[e_k \pmid h_{i}\cdot b\cdot c_{k}] \gt 0\), then \(P[e_k \pmid h_{j}\cdot b\cdot c_{k}] \gt 0\). Equivalently, \(h_j\) is fails to be fully outcome-compatible with \(h_i\) on experiment or observation \(c_k\) just when , for at least one of its possible outcomes \(e_k\), \(P[e_k \pmid h_{i}\cdot b\cdot c_{k}] \gt 0\) but \(P[e_k \pmid h_{j}\cdot b\cdot c_{k}] = 0\).

The first part of the Likelihood Ratio Convergence Theorem applies to that part of the total stream of evidence (i.e., that subsequence of the total evidence stream) on which hypothesis \(h_j\) fails to be fully outcome-compatible with hypothesis \(h_i\); the second part of the theorem applies to the remaining part of the total stream of evidence, that subsequence of the total evidence stream on which \(h_j\) is fully outcome-compatible with \(h_i\). It turns out that these two kinds of cases must be treated differently. (This is due to the way in which the expected information content for empirically distinguishing between the two hypotheses will be measured for experiments and observations that are fully outcome compatible ; this measure of information content blows up (becomes infinite) for experiments and observations that fail to be fully outcome compatible ). Thus, the following part of the convergence theorem applies to just that part of the total stream of evidence that consists of experiments and observations that fail to be fully outcome compatible for the pair of hypotheses involved. Here, then, is the first part of the convergence theorem.

Likelihood Ratio Convergence Theorem 1—The Falsification Theorem: Suppose that the total stream of evidence \(c^n\) contains precisely m experiments or observations on which \(h_j\) fails to be fully outcome-compatible with \(h_i\). And suppose that the Independent Evidence Conditions hold for evidence stream \(c^n\) with respect to each of these two hypotheses. Furthermore, suppose there is a lower bound \(\delta \gt 0\) such that for each \(c_k\) on which \(h_j\) fails to be fully outcome-compatible with \(h_i\),

—i.e., \(h_i\) together with \(b\cdot c_k\) says , with likelihood at least as large as \(\delta\), that one of the outcomes will occur that \(h_j\) says cannot occur. Then,

which approaches 1 for large m . (For proof see Proof of the Falsification Theorem .)

In other words, we only suppose that for each of m observations, \(c_k, h_i\) says observation \(c_k\) has at least a small likelihood \(\delta\) of producing one of the outcomes \(o_{ku}\) that \(h_j\) says is impossible. If the number m of such experiments or observations is large enough (or if the lower bound \(\delta\) on the likelihoods of getting such outcomes is large enough), and if \(h_i\) (together with \(b\cdot c^n)\) is true, then it is highly likely that one of the outcomes held to be impossible by \(h_j\) will actually occur. If one of these outcomes does occur, then the likelihood ratio for \(h_j\) as compared to over \(h_i\) will become 0. According to Bayes’ Theorem, when this happen, \(h_j\) is absolutely refuted by the evidence—its posterior probability becomes 0.

The Falsification Theorem is quite commonsensical. First, notice that if there is a crucial experiment in the evidence stream, the theorem is completely obvious. That is, suppose for the specific experiment \(c_k\) (in evidence stream \(c^n)\) there are two incompatible possible outcomes \(o_{kv}\) and \(o_{ku}\) such that \(P[o_{kv} \pmid h_{j}\cdot b\cdot c_{k}] = 1\) and \(P[o_{ku} \pmid h_{i}\cdot b\cdot c_{k}] = 1\). Then, clearly, \(P[\vee \{ o_{ku}: P[o_{ku} \pmid h_{j}\cdot b\cdot c_{k}] = 0\} \pmid h_{i}\cdot b\cdot c_{k}] = 1\), since \(o_{ku}\) is one of the \(o_{ku}\) such that \(P[o_{ku} \pmid h_{j}\cdot b\cdot c_{k}] = 0\). So, where a crucial experiment is available, the theorem applies with \(m = 1\) and \(\delta = 1\).

The theorem is equally commonsensical for cases where no crucial experiment is available. To see what it says in such cases, consider an example. Let \(h_i\) be some theory that implies a specific rate of proton decay, but a rate so low that there is only a very small probability that any particular proton will decay in a given year. Consider an alternative theory \(h_j\) that implies that protons never decay. If \(h_i\) is true, then for a persistent enough sequence of observations (i.e., if proper detectors can keep trillions of protons under observation for long enough), eventually a proton decay will almost surely be detected. When this happens, the likelihood ratio becomes 0. Thus, the posterior probability of \(h_j\) becomes 0.

It is instructive to plug some specific values into the formula given by the Falsification Theorem, to see what the convergence rate might look like. For example, the theorem tells us that if we compare any pair of hypotheses \(h_i\) and \(h_j\) on an evidence stream \(c^n\) that contains at least \(m = 19\) observations or experiments, where each has a likelihood \(\delta \ge .10\) of yielding a falsifying outcome , then the likelihood (on \(h_{i}\cdot b\cdot c^{n})\) of obtaining an outcome sequence \(e^n\) that yields likelihood-ratio

will be at least as large as \((1 - (1-.1)^{19}) = .865\). (The reader is invited to try other values of \(\delta\) and m .)

A comment about the need for and usefulness of such convergence theorems is in order, now that we’ve seen one. Given some specific pair of scientific hypotheses \(h_i\) and \(h_j\) one may directly compute the likelihood, given \((h_{i}\cdot b\cdot c^{n})\), that a proposed sequence of experiments or observations \(c^n\) will result in one of the sequences of outcomes that would yield low likelihood ratios. So, given a specific pair of hypotheses and a proposed sequence of experiments, we don’t need a general Convergence Theorem to tell us the likelihood of obtaining refuting evidence. The specific hypotheses \(h_i\) and \(h_j\) tell us this themselves . They tell us the likelihood of obtaining each specific outcome stream, including those that either refute the competitor or produce a very small likelihood ratio for it. Furthermore, after we’ve actually performed an experiment and recorded its outcome, all that matters is the actual ratio of likelihoods for that outcome. Convergence theorems become moot.

The point of the Likelihood Ratio Convergence Theorem (both the Falsification Theorem and the part of the theorem still to come) is to assure us in advance of considering any specific pair of hypotheses that if the possible evidence streams that test hypotheses have certain characteristics which reflect the empirical distinctness of the two hypotheses, then it is highly likely that one of the sequences of outcomes will occur that yields a very small likelihood ratio. These theorems provide finite lower bounds on how quickly such convergence is likely to be. Thus, they show that the CoA is satisfied in advance of our using the logic to test specific pairs of hypotheses against one another.

The Falsification Theorem applies whenever the evidence stream includes possible outcomes that may falsify the alternative hypothesis. However, it completely ignores the influence of any experiments or observations in the evidence stream on which hypothesis \(h_j\) is fully outcome-compatible with hypothesis \(h_i\). We now turn to a theorem that applies to those evidence streams (or to parts of evidence streams) consisting only of experiments and observations on which hypothesis \(h_j\) is fully outcome-compatible with hypothesis \(h_i\). Evidence streams of this kind contain no possibly falsifying outcomes. In such cases the only outcomes of an experiment or observation \(c_k\) for which hypothesis \(h_j\) may specify 0 likelihoods are those for which hypothesis \(h_i\) specifies 0 likelihoods as well.

Hypotheses whose connection with the evidence is entirely statistical in nature will usually be fully outcome-compatible on the entire evidence stream. So, evidence streams of this kind are undoubtedly much more common in practice than those containing possibly falsifying outcomes. Furthermore, whenever an entire stream of evidence contains some mixture of experiments and observations on which the hypotheses are not fully outcome compatible along with others on which they are fully outcome compatible , we may treat the experiments and observations for which full outcome compatibility holds as a separate subsequence of the entire evidence stream, to see the likely impact of that part of the evidence in producing values for likelihood ratios.

To cover evidence streams (or subsequences of evidence streams) consisting entirely of experiments or observations on which \(h_j\) is fully outcome-compatible with hypothesis \(h_i\) we will first need to identify a useful way to measure the degree to which hypotheses are empirically distinct from one another on such evidence. Consider some particular sequence of outcomes \(e^n\) that results from observations \(c^n\). The likelihood ratio \(P[e^n \pmid h_{j}\cdot b\cdot c^{n}] / P[e^n \pmid h_{i}\cdot b\cdot c^{n}]\) itself measures the extent to which the outcome sequence distinguishes between \(h_i\) and \(h_j\). But as a measure of the power of evidence to distinguish among hypotheses, raw likelihood ratios provide a rather lopsided scale, a scale that ranges from 0 to infinity with the midpoint, where \(e^n\) doesn’t distinguish at all between \(h_i\) and \(h_j\), at 1. So, rather than using raw likelihood ratios to measure the ability of \(e^n\) to distinguish between hypotheses, it proves more useful to employ a symmetric measure. The logarithm of the likelihood ratio provides such a measure.

Definition: QI—the Quality of the Information . For each experiment or observation \(c_k\), define the quality of the information provided by possible outcome \(o_{ku}\) for distinguishing \(h_j\) from \(h_i\), given b , as follows (where henceforth we take “logs” to be base-2):

Similarly, for the sequence of experiments or observations \(c^n\), define the quality of the information provided by possible outcome \(e^n\) for distinguishing \(h_j\) from \(h_i\), given b , as follows:

That is, QI is the base-2 logarithm of the likelihood ratio for \(h_i\) over that for \(h_j\).

So, we’ll measure the Quality of the Information an outcome would yield in distinguishing between two hypotheses as the base-2 logarithm of the likelihood ratio. This is clearly a symmetric measure of the outcome’s evidential strength at distinguishing between the two hypotheses. On this measure hypotheses \(h_i\) and \(h_j\) assign the same likelihood value to a given outcome \(o_{ku}\) just when \(\QI[o_{ku} \pmid h_i /h_j \pmid b\cdot c_k] = 0\). Thus, QI measures information on a logarithmic scale that is symmetric about the natural no-information midpoint, 0. This measure is set up so that positive information favors \(h_i\) over \(h_j\), and negative information favors \(h_j\) over \(h_i\).

Given the Independent Evidence Assumptions with respect to each hypothesis, it’s easy to show that the QI for a sequence of outcomes is just the sum of the QIs of the individual outcomes in the sequence:

Probability theorists measure the expected value of a quantity by first multiplying each of its possible values by their probabilities of occurring, and then summing these products. Thus, the expected value of QI is given by the following formula:

Definition: EQI—the Expected Quality of the Information . We adopt the convention that if \(P[o_{ku} \pmid h_{i}\cdot b\cdot c_{k}] = 0\), then the term \(\QI[o_{ku} \pmid h_i /h_j \pmid b\cdot c_k] \times P[o_{ku} \pmid h_{i}\cdot b\cdot c_{k}] = 0\). This convention will make good sense in the context of the following definition because, whenever the outcome \(o_{ku}\) has 0 probability of occurring according to \(h_i\) (together with \(b\cdot c_k)\), it makes good sense to give it 0 impact on the ability of the evidence to distinguish between \(h_j\) and \(h_i\) when \(h_i\) (together with \(b\cdot c_k)\) is true. Also notice that the full outcome-compatibility of \(h_j\) with \(h_i\) on \(c_k\) means that whenever \(P[e_k \pmid h_{j}\cdot b\cdot c_{k}] = 0\), we must have \(P[e_k \pmid h_{i}\cdot b\cdot c_{k}] = 0\) as well; so whenever the denominator would be 0 in the term

the convention just described makes the term

Thus the following notion is well-defined:

For \(h_j\) fully outcome-compatible with \(h_i\) on experiment or observation \(c_k\), define

Also, for \(h_j\) fully outcome-compatible with \(h_i\) on each experiment and observation in the sequence \(c^n\), define

The EQI of an experiment or observation is the Expected Quality of its Information for distinguishing \(h_i\) from \(h_j\) when \(h_i\) is true. It is a measure of the expected evidential strength of the possible outcomes of an experiment or observation at distinguishing between the hypotheses when \(h_i\) (together with \(b\cdot c)\) is true. Whereas QI measures the ability of each particular outcome or sequence of outcomes to empirically distinguish hypotheses, EQI measures the tendency of experiments or observations to produce distinguishing outcomes. It can be shown that EQI tracks empirical distinctness in a very precise way. We return to this in a moment.

It is easily seen that the EQI for a sequence of observations \(c^n\) is just the sum of the EQIs of the individual observations \(c_k\) in the sequence:

(For proof see the supplement Proof that the EQI for \(c^n\) is the sum of the EQI for the individual \(c_k\) .)

This suggests that it may be useful to average the values of the \(\EQI[c_k \pmid h_i /h_j \pmid b]\) over the number of observations n to obtain a measure of the average expected quality of the information among the experiments and observations that make up the evidence stream \(c^n\).

Definition: The Average Expected Quality of Information For \(h_j\) fully outcome-compatible with \(h_i\) on each experiment and observation in the evidence stream \(c^n\), define the average expected quality of information, \(\bEQI\), from \(c^n\) for distinguishing \(h_j\) from \(h_i\), given \(h_i\cdot b\), as follows:

It turns out that the value of \(\EQI[c_k \pmid h_i /h_j \pmid b_{}]\) cannot be less than 0; and it must be greater than 0 just in case \(h_i\) is empirically distinct from \(h_j\) on at least one outcome \(o_{ku}\)—i.e., just in case it is empirically distinct in the sense that \(P[o_{ku} \pmid h_{i}\cdot b\cdot c_{k}] \ne P[o_{ku} \pmid h_{j}\cdot b\cdot c_{k}]\), for at least one outcome \(o_{ku}\). The same goes for the average, \(\bEQI[c^n \pmid h_i /h_j \pmid b]\).

Theorem: Nonnegativity of EQI.

\(\EQI[c_k \pmid h_i /h_j \pmid b_{}] \ge 0\); and \(\EQI[c_k \pmid h_i /h_j \pmid b_{}] \gt 0\) if and only if for at least one of its possible outcomes \(o_{ku}\),

As a result, \(\bEQI[c^n \pmid h_i /h_j \pmid b] \ge 0\); and \(\bEQI[c^n \pmid h_i /h_j \pmid b] \gt 0\) if and only if at least one experiment or observation \(c_k\) has at least one possible outcome \(o_{ku}\) such that

(For proof, see the supplement The Effect on EQI of Partitioning the Outcome Space More Finely—Including Proof of the Nonnegativity of EQI .)

In fact, the more finely one partitions the outcome space \(O_{k} = \{o_{k1},\ldots ,o_{kv},\ldots ,o_{kw}\}\) into distinct outcomes that differ on likelihood ratio values, the larger EQI becomes. [ 15 ] This shows that EQI tracks empirical distinctness in a precise way. The importance of the Non-negativity of EQI result for the Likelihood Ratio Convergence Theorem will become clear in a moment.

We are now in a position to state the second part of the Likelihood Ratio Convergence Theorem . It applies to all evidence streams not containing possibly falsifying outcomes for \(h_j\) when \(h_i\) holds—i.e., it applies to all evidence streams for which \(h_j\) is fully outcome-compatible with \(h_i\) on each \(c_k\) in the stream.

Likelihood Ratio Convergence Theorem 2—The Probabilistic Refutation Theorem.

Suppose the evidence stream \(c^n\) contains only experiments or observations on which \(h_j\) is fully outcome-compatible with \(h_i\)—i.e., suppose that for each condition \(c_k\) in sequence \(c^n\), for each of its possible outcomes possible outcomes \(o_{ku}\), either \(P[o_{ku} \pmid h_{i}\cdot b\cdot c_{k}] = 0\) or \(P[o_{ku} \pmid h_{j}\cdot b\cdot c_{k}] \gt 0\). In addition (as a slight strengthening of the previous supposition), for some \(\gamma \gt 0\) a number smaller than \(1/e^2\) (\(\approx .135\); where e ’ is the base of the natural logarithm), suppose that for each possible outcome \(o_{ku}\) of each observation condition \(c_k\) in \(c^n\), either \(P[o_{ku} \pmid h_{i}\cdot b\cdot c_{k}] = 0\) or

And suppose that the Independent Evidence Conditions hold for evidence stream \(c^n\) with respect to each of these hypotheses. Now, choose any positive \(\varepsilon \lt 1\), as small as you like, but large enough (for the number of observations n being contemplated) that the value of

For \(\varepsilon = 1/2^m\) and \(\gamma = 1/2^q\), this formula becomes,

(For proof see the supplement Proof of the Probabilistic Refutation Theorem .)

This theorem provides sufficient conditions for the likely refutation of false alternatives via exceeding small likelihood ratios. The conditions under which this happens characterize the degree to which the hypotheses involved are empirically distinct from one another. The theorem says that when these conditions are met, according to hypothesis \(h_i\) (taken together with \(b\cdot c^n)\), the likelihood is near 1 that that one of the outcome sequence \(e^n\) will occur for which the likelihood ratio is smaller than \(\varepsilon\) (for any value of \(\varepsilon\) you may choose). The likelihood of getting such an evidential outcome \(e^n\) is quite close to 1—i.e., no more than the amount

below 1. (Notice that this amount below 1 goes to 0 as n increases.)

It turns out that in almost every case (for almost any pair of hypotheses) the actual likelihood of obtaining such evidence (i.e., evidence that has a likelihood ratio value less than \(\varepsilon)\) will be much closer to 1 than this factor indicates. [ 16 ] Thus, the theorem provides an overly cautious lower bound on the likelihood of obtaining small likelihood ratios. It shows that the larger the value of \(\bEQI\) for an evidence stream, the more likely that stream is to produce a sequence of outcomes that yield a very small likelihood ratio value. But even if \(\bEQI\) remains quite small, a long enough evidence stream, n , of such low-grade evidence will, nevertheless, almost surely produce an outcome sequence having a very small likelihood ratio value. [ 17 ]

Notice that the antecedent condition of the theorem, that “either

for some \(\gamma \gt 0\) but less than \(1/e^2\) (\(\approx .135\))”, does not favor hypothesis \(h_i\) over \(h_j\) in any way. The condition only rules out the possibility that some outcomes might furnish extremely strong evidence against \(h_j\) relative to \(h_i\)—by making \(P[o_{ku} \pmid h_{i}\cdot b\cdot c_{k}] = 0\) or by making

less than some quite small \(\gamma\). This condition is only needed because our measure of evidential distinguishability, QI, blows up when the ratio

is extremely small. Furthermore, this condition is really no restriction at all on possible experiments or observations. If \(c_k\) has some possible outcome sentence \(o_{ku}\) that would make

(for a given small \(\gamma\) of interest), one may disjunctively lump \(o_{ku}\) together with some other outcome sentence \(o_{kv}\) for \(c_k\). Then, the antecedent condition of the theorem will be satisfied, but with the sentence ‘\((o_{ku} \vee o_{kv})\)’ treated as a single outcome. It can be proved that the only effect of such “disjunctive lumping” is to make \(\bEQI\) smaller than it would otherwise be (whereas larger values of \(\bEQI\) are more desirable). If the too strongly refuting disjunct \(o_{ku}\) actually occurs when the experiment or observation \(c_k\) is conducted, all the better, since this results in a likelihood ratio

smaller than \(\gamma\) on that particular evidential outcome. We merely failed to take this more strongly refuting possibility into account when computing our lower bound on the likelihood that refutation via likelihood ratios would occur.

The point of the two Convergence Theorems explored in this section is to assure us, in advance of the consideration of any specific pair of hypotheses, that if the possible evidence streams that test them have certain characteristics which reflect their evidential distinguishability, it is highly likely that outcomes yielding small likelihood ratios will result. These theorems provide finite lower bounds on how quickly convergence is likely to occur. Thus, there is no need to wait through some infinitely long run for convergence to occur. Indeed, for any evidence sequence on which the probability distributions are at all well behaved, the actual likelihood of obtaining outcomes that yield small likelihood ratio values will inevitably be much higher than the lower bounds given by Theorems 1 and 2.

In sum, according to Theorems 1 and 2, each hypothesis \(h_i\) says , via likelihoods, that given enough observations, it is very likely to dominate its empirically distinct rivals in a contest of likelihood ratios. The true hypothesis speaks truthfully about this, and its competitors lie. Even a sequence of observations with an extremely low average expected quality of information is very likely to do the job if that evidential sequence is long enough. Thus (by Equation 9* ), as evidence accumulates, the degree of support for false hypotheses will very probably approach 0, indicating that they are probably false; and as this happens, (by Equations 10 and 11) the degree of support for the true hypothesis will approach 1, indicating its probable truth. Thus, the Criterion of Adequacy (CoA) is satisfied.

Up to this point we have been supposing that likelihoods possess objective or agreed numerical values. Although this supposition is often satisfied in scientific contexts, there are important settings where it is unrealistic, where hypotheses only support vague likelihood values, and where there is enough ambiguity in what hypotheses say about evidential claims that the scientific community cannot agree on precise values for the likelihoods of evidential claims. [ 18 ] Let us now see how the supposition of precise, agreed likelihood values may be relaxed in a reasonable way.

Recall why agreement, or near agreement, on precise values for likelihoods is so important to the scientific enterprise. To the extent that members of a scientific community disagree on the likelihoods, they disagree about the empirical content of their hypotheses, about what each hypothesis says about how the world is likely to be. This can lead to disagreement about which hypotheses are refuted or supported by a given body of evidence. Similarly, to the extent that the values of likelihoods are only vaguely implied by hypotheses as understood by an individual agent, that agent may be unable to determine which of several hypotheses is refuted or supported by a given body of evidence.

We have seen, however, that the individual values of likelihoods are not really crucial to the way evidence impacts hypotheses. Rather, as Equations 9–11 show, it is ratios of likelihoods that do the heavy lifting. So, even if two support functions \(P_{\alpha}\) and \(P_{\beta}\) disagree on the values of individual likelihoods, they may, nevertheless, largely agree on the refutation or support that accrues to various rival hypotheses, provided that the following condition is satisfied:

• whenever possible outcome sequence \(e^n\) makes \[\frac{P_{\alpha}[e^n \pmid h_{j}\cdot b\cdot c^{n}]}{P_{\alpha}[e^n \pmid h_{i}\cdot b\cdot c^{n}]} \lt 1,\] it also makes \[\frac{P_{\beta}[e^n \pmid h_{j}\cdot b\cdot c^{n}]}{P_{\beta}[e^n \pmid h_{i}\cdot b\cdot c^{n}]} \lt 1;\]
• whenever possible outcome sequence \(e^n\) makes \[\frac{P_{\alpha}[e^n \pmid h_{j}\cdot b\cdot c^{n}]}{P_{\alpha}[e^n \pmid h_{i}\cdot b\cdot c^{n}]} \gt 1,\] it also makes \[\frac{P_{\beta}[e^n \pmid h_{j}\cdot b\cdot c^{n}]}{P_{\beta}[e^n \pmid h_{i}\cdot b\cdot c^{n}]} \gt 1;\]
• each of these likelihood ratios is either close to 1 for both of these support functions, or is quite far from 1 for both of them. [ 19 ]

When this condition holds, the evidence will support \(h_i\) over \(h_j\) according to \(P_{\alpha}\) just in case it does so for \(P_{\beta}\) as well, although the strength of support may differ. Furthermore, although the rate at which the likelihood ratios increase or decrease on a stream of evidence may differ for the two support functions, the impact of the cumulative evidence should ultimately affect their refutation or support in much the same way.

When likelihoods are vague or diverse, we may take an approach similar to that we employed for vague and diverse prior plausibility assessments. We may extend the vagueness sets for individual agents to include a collection of inductive support functions that cover the range of values for likelihood ratios of evidence claims (as well as cover the ranges of comparative support strengths for hypotheses due to plausibility arguments within b , as represented by ratios of prior probabilities). Similarly, we may extend the diversity sets for communities of agents to include support functions that cover the ranges of likelihood ratio values that arise within the vagueness sets of members of the scientific community.

This broadening of vagueness and diversity sets to accommodate vague and diverse likelihood values makes no trouble for the convergence to truth results for hypotheses. For, provided that the Directional Agreement Condition is satisfied by all support functions in an extended vagueness or diversity set under consideration, the Likelihood Ratio Convergence Theorem applies to each individual support function in that set. For, the proof of that convergence theorem doesn’t depend on the supposition that likelihoods are objective or have intersubjectively agreed values. Rather, it applies to each individual support function \(P_{\alpha}\). The only possible problem with applying this result across a range of support functions is that when their values for likelihoods differ, function \(P_{\alpha}\) may disagree with \(P_{\beta}\) on which of the hypotheses is favored by a given sequence of evidence. That can happen because different support functions may represent the evidential import of hypotheses differently, by specifying different likelihood values for the very same evidence claims. So, an evidence stream that favors \(h_i\) according to \(P_{\alpha}\) may instead favor \(h_j\) according to \(P_{\beta}\). However, when the Directional Agreement Condition holds for a given collection of support functions, this problem cannot arise. Directional Agreement means that the evidential import of hypotheses is similar enough for \(P_{\alpha}\) and \(P_{\beta}\) that a sequence of outcomes may favor a hypothesis according to \(P_{\alpha}\) only if it does so for \(P_{\beta}\) as well.

Thus, when the Directional Agreement Condition holds for all support functions in a vagueness or diversity set that is extended to include vague or diverse likelihoods, and provided that enough evidentially distinguishing experiments or observations can be performed, all support functions in the extended vagueness or diversity set will very probably come to agree that the likelihood ratios for empirically distinct false competitors of a true hypothesis are extremely small. As that happens, the community comes to agree on the refutation of these competitors, and the true hypothesis rises to the top of the heap. [ 20 ]

What if the true hypothesis has evidentially equivalent rivals? Their posterior probabilities must rise as well. In that case we are only assured that the disjunction of the true hypothesis with its evidentially equivalent rivals will be driven to 1 as evidence lays low its evidentially distinct rivals. The true hypothesis will itself approach 1 only if either it has no evidentially equivalent rivals, or whatever equivalent rivals it does have can be laid low by plausibility arguments of a kind that don’t depend on the evidential likelihoods, but only show up via the comparative plausibility assessments represented by ratios of prior probabilities.

• Enumerative Inductions: Bayesian Estimation and Convergence
• Some Prominent Approaches to the Representation of Uncertain Inference
• Likelihood Ratios, Likelihoodism, and the Law of Likelihood
• Immediate Consequences of the Independent Evidence Conditions
• Proof of the Falsification Theorem
• Proof that the EQI for \(c^n\) is the sum of EQI for the individual \(c_k\)
• The Effect on EQI of Partitioning the Outcome Space More Finely—Including Proof of the Nonnegativity of EQI
• Proof of the Probabilistic Refutation Theorem
• Boole, George, 1854, The Laws of Thought , London: MacMillan. Republished in 1958 by Dover: New York.
• Bovens, Luc and Stephan Hartmann, 2003, Bayesian Epistemology , Oxford: Oxford University Press. doi:10.1093/0199269750.001.0001
• Carnap, Rudolf, 1950, Logical Foundations of Probability , Chicago: University of Chicago Press.
• –––, 1952, The Continuum of Inductive Methods , Chicago: University of Chicago Press.
• –––, 1963, “Replies and Systematic Expositions”, in The Philosophy of Rudolf Carnap , Paul Arthur Schilpp (ed.),La Salle, IL: Open Court.
• Chihara, Charles S., 1987, “Some Problems for Bayesian Confirmation Theory”, British Journal for the Philosophy of Science , 38(4): 551–560. doi:10.1093/bjps/38.4.551
• Christensen, David, 1999, “Measuring Confirmation”, Journal of Philosophy , 96(9): 437–61. doi:10.2307/2564707
• –––, 2004, Putting Logic in its Place: Formal Constraints on Rational Belief , Oxford: Oxford University Press. doi:10.1093/0199263256.001.0001
• De Finetti, Bruno, 1937, “La Prévision: Ses Lois Logiques, Ses Sources Subjectives”, Annales de l’Institut Henri Poincaré , 7: 1–68; translated by Henry E. Kyburg, Jr. as “Foresight. Its Logical Laws, Its Subjective Sources”, in Studies in Subjective Probability , Henry E. Kyburg, Jr. and H.E. Smokler (eds.), Robert E. Krieger Publishing Company, 1980.
• Dowe, David L., Steve Gardner, and Graham Oppy, 2007, “Bayes, Not Bust! Why Simplicity is No Problem for Bayesians”, British Journal for the Philosophy of Science , 58(4): 709–754. doi:10.1093/bjps/axm033
• Dubois, Didier J. and Henri Prade, 1980, Fuzzy Sets and Systems , (Mathematics in Science and Engineering, 144), New York: Academic Press.
• –––, 1990, “An Introduction to Possibilistic and Fuzzy Logics”, in Glenn Shafer and Judea Pearl (eds.), Readings in Uncertain Reasoning , San Mateo, CA: Morgan Kaufmann, 742–761..
• Duhem, P., 1906, La theorie physique. Son objet et sa structure , Paris: Chevalier et Riviere; translated by P.P. Wiener, The Aim and Structure of Physical Theory , Princeton, NJ: Princeton University Press, 1954.
• Earman, John, 1992, Bayes or Bust? A Critical Examination of Bayesian Confirmation Theory , Cambridge, MA: MIT Press.
• Edwards, A.W.F., 1972, Likelihood: an account of the statistical concept of likelihood and its application to scientific inference , Cambridge: Cambridge University Press.
• Edwards, Ward, Harold Lindman, and Leonard J. Savage, 1963, “Bayesian Statistical Inference for Psychological Research”, Psychological Review , 70(3): 193–242. doi:10.1037/h0044139
• Eells, Ellery, 1985, “Problems of Old Evidence”, Pacific Philosophical Quarterly , 66(3–4): 283–302. doi:10.1111/j.1468-0114.1985.tb00254.x
• –––, 2006, “Confirmation Theory”, Sarkar and Pfeifer 2006..
• Eells, Ellery and Branden Fitelson, 2000, “Measuring Confirmation and Evidence”, Journal of Philosophy , 97(12): 663–672. doi:10.2307/2678462
• Field, Hartry H., 1977, “Logic, Meaning, and Conceptual Role”, Journal of Philosophy , 74(7): 379–409. doi:10.2307/2025580
• Fisher, R.A., 1922, “On the Mathematical Foundations of Theoretical Statistics”, Philosophical Transactions of the Royal Society, series A , 222(594–604): 309–368. doi:10.1098/rsta.1922.0009
• Fitelson, Branden, 1999, “The Plurality of Bayesian Measures of Confirmation and the Problem of Measure Sensitivity”, Philosophy of Science , 66: S362–S378. doi:10.1086/392738
• –––, 2001, “A Bayesian Account of Independent Evidence with Applications”, Philosophy of Science , 68(S3): S123–S140. doi:10.1086/392903
• –––, 2002, “Putting the Irrelevance Back Into the Problem of Irrelevant Conjunction”, Philosophy of Science , 69(4): 611–622. doi:10.1086/344624
• –––, 2006, “Inductive Logic”, Sarkar and Pfeifer 2006..
• –––, 2006, “Logical Foundations of Evidential Support”, Philosophy of Science , 73(5): 500–512. doi:10.1086/518320
• –––, 2007, “Likelihoodism, Bayesianism, and Relational Confirmation”, Synthese , 156(3): 473–489. doi:10.1007/s11229-006-9134-9
• Fitelson, Branden and James Hawthorne, 2010, “How Bayesian Confirmation Theory Handles the Paradox of the Ravens”, in Eells and Fetzer (eds.), The Place of Probability in Science , Open Court. [ Fitelson & Hawthorne 2010 preprint available from the author (PDF) ]
• Forster, Malcolm and Elliott Sober, 2004, “Why Likelihood”, in Mark L. Taper and Subhash R. Lele (eds.), The Nature of Scientific Evidence , Chicago: University of Chicago Press.
• Friedman, Nir and Joseph Y. Halpern, 1995, “Plausibility Measures: A User’s Guide”, in UAI 95: Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence , 175–184.
• Gaifman, Haim and Marc Snir, 1982, “Probabilities Over Rich Languages, Testing and Randomness”, Journal of Symbolic Logic , 47(3): 495–548. doi:10.2307/2273587
• Gillies, Donald, 2000, Philosophical Theories of Probability , London: Routledge.
• Glymour, Clark N., 1980, Theory and Evidence , Princeton, NJ: Princeton University Press.
• Goodman, Nelson, 1983, Fact, Fiction, and Forecast , 4 th edition, Cambridge, MA: Harvard University Press.
• Hacking, Ian, 1965, Logic of Statistical Inference , Cambridge: Cambridge University Press.
• –––, 1975, The Emergence of Probability: a Philosophical Study of Early Ideas about Probability, Induction and Statistical Inference , Cambridge: Cambridge University Press. doi:10.1017/CBO9780511817557
• –––, 2001, An Introduction to Probability and Inductive Logic , Cambridge: Cambridge University Press. doi:10.1017/CBO9780511801297
• Hájek, Alan, 2003a, “What Conditional Probability Could Not Be”, Synthese , 137(3):, 273–323. doi:10.1023/B:SYNT.0000004904.91112.16
• –––, 2003b, “Interpretations of the Probability Calculus”, in the Stanford Encyclopedia of Philosophy , (Summer 2003 Edition), Edward N. Zalta (ed.), URL = < https://plato.stanford.edu/archives/sum2003/entries/probability-interpret/ >
• –––, 2005, “Scotching Dutch Books?” Philosophical Perspectives , 19 (Epistemology): 139–151. doi:10.1111/j.1520-8583.2005.00057.x
• –––, 2007, “The Reference Class Problem is Your Problem Too”, Synthese , 156(3): 563–585. doi:10.1007/s11229-006-9138-5
• Halpern, Joseph Y., 2003, Reasoning About Uncertainty , Cambridge, MA: MIT Press.
• Harper, William L., 1976, “Rational Belief Change, Popper Functions and Counterfactuals”, in Harper and Hooker 1976: 73–115. doi:10.1007/978-94-010-1853-1_5
• Harper, William L. and Clifford Alan Hooker (eds.), 1976, Foundations of Probability Theory, Statistical Inference, and Statistical Theories of Science, volume I Foundations and Philosophy of Epistemic Applications of Probability Theory , (The Western Ontario Series in Philosophy of Science, 6a), Dordrecht: Reidel. doi:10.1007/978-94-010-1853-1
• Hawthorne, James, 1993, “Bayesian Induction is Eliminative Induction”, Philosophical Topics , 21(1): 99–138. doi:10.5840/philtopics19932117
• –––, 1994,“On the Nature of Bayesian Convergence”, PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association 1994 , 1: 241–249. doi:10.1086/psaprocbienmeetp.1994.1.193029
• –––, 2005, “ Degree-of-Belief and Degree-of-Support : Why Bayesians Need Both Notions”, Mind , 114(454): 277–320. doi:10.1093/mind/fzi277
• –––, 2009, “The Lockean Thesis and the Logic of Belief”, in Franz Huber and Christoph Schmidt-Petri (eds.), Degrees of Belief , (Synthese Library, 342), Dordrecht: Springer, pp. 49–74. doi:10.1007/978-1-4020-9198-8_3
• Hawthorne, James and Luc Bovens, 1999, “The Preface, the Lottery, and the Logic of Belief”, Mind , 108(430): 241–264. doi:10.1093/mind/108.430.241
• Hawthorne, James and Branden Fitelson, 2004, “Discussion: Re-solving Irrelevant Conjunction With Probabilistic Independence”, Philosophy of Science , 71(4): 505–514. doi:10.1086/423626
• Hellman, Geoffrey, 1997, “Bayes and Beyond”, Philosophy of Science , 64(2): 191–221. doi:10.1086/392548
• Hempel, Carl G., 1945, “Studies in the Logic of Confirmation”, Mind , 54(213): 1–26, 54(214):97–121. doi:10.1093/mind/LIV.213.1 doi:10.1093/mind/LIV.214.97
• Horwich, Paul, 1982, Probability and Evidence , Cambridge: Cambridge University Press. doi:10.1017/CBO9781316494219
• Howson, Colin, 1997, “A Logic of Induction”, Philosophy of Science , 64(2): 268–290. doi:10.1086/392551
• –––, 2000, Hume’s Problem: Induction and the Justification of Belief , Oxford: Oxford University Press. doi:10.1093/0198250371.001.0001
• –––, 2002, “Bayesianism in Statistics“, in Swinburne 2002: 39–71. doi:10.5871/bacad/9780197263419.003.0003
• –––, 2007, “Logic With Numbers”, Synthese , 156(3): 491–512. doi:10.1007/s11229-006-9135-8
• Howson, Colin and Peter Urbach, 1993, Scientific Reasoning: The Bayesian Approach , La Salle, IL: Open Court. [3rd edition, 2005.]
• Huber, Franz, 2005a, “Subjective Probabilities as Basis for Scientific Reasoning?” British Journal for the Philosophy of Science , 56(1): 101–116. doi:10.1093/phisci/axi105
• –––, 2005b, “What Is the Point of Confirmation?” Philosophy of Science , 72(5): 1146–1159. doi:10.1086/508961
• Jaynes, Edwin T., 1968, “Prior Probabilities”, IEEE Transactions on Systems Science and Cybernetics , SSC–4(3): 227–241. doi:10.1109/TSSC.1968.300117
• Jeffrey, Richard C., 1983, The Logic of Decision , 2nd edition, Chicago: University of Chicago Press.
• –––, 1987, “Alias Smith and Jones: The Testimony of the Senses”, Erkenntnis , 26(3): 391–399. doi:10.1007/BF00167725
• –––, 1992, Probability and the Art of Judgment , New York: Cambridge University Press. doi:10.1017/CBO9781139172394
• –––, 2004, Subjective Probability: The Real Thing , Cambridge: Cambridge University Press. doi:10.1017/CBO9780511816161
• Jeffreys, Harold, 1939, Theory of Probability , Oxford: Oxford University Press.
• Joyce, James M., 1998, “A Nonpragmatic Vindication of Probabilism”, Philosophy of Science , 65(4): 575–603. doi:10.1086/392661
• –––, 1999, The Foundations of Causal Decision Theory , New York: Cambridge University Press. doi:10.1017/CBO9780511498497
• –––, 2003, “Bayes’ Theorem”, in the Stanford Encyclopedia of Philosophy , (Summer 2003 Edition), Edward N. Zalta (ed.), URL = < https://plato.stanford.edu/archives/win2003/entries/bayes-theorem/ >
• –––, 2004, “Bayesianism”, in Alfred R. Mele and Piers Rawling (eds.), The Oxford Handbook of Rationality , Oxford: Oxford University Press, pp. 132–153. doi:10.1093/0195145399.003.0008
• –––, 2005, “How Probabilities Reflect Evidence”, Philosophical Perspectives , 19: 153–179. doi:10.1111/j.1520-8583.2005.00058.x
• Kaplan, Mark, 1996, Decision Theory as Philosophy , Cambridge: Cambridge University Press.
• Kelly, Kevin T., Oliver Schulte, and Cory Juhl, 1997, “Learning Theory and the Philosophy of Science”, Philosophy of Science , 64(2): 245–267. doi:10.1086/392550
• Keynes, John Maynard, 1921, A Treatise on Probability , London: Macmillan and Co.
• Kolmogorov, A.N., 1956, Foundations of the Theory of Probability ( Grundbegriffe der Wahrscheinlichkeitsrechnung , 2 nd edition, New York: Chelsea Publishing Company.
• Koopman, B.O., 1940, “The Bases of Probability”, Bulletin of the American Mathematical Society , 46(10): 763–774. Reprinted in H. Kyburg and H. Smokler (eds.), 1980, Studies in Subjective Probability , 2nd edition, Huntington, NY: Krieger Publ. Co. [ Koopman 1940 available online ]
• Kyburg, Henry E., Jr., 1974, The Logical Foundations of Statistical Inference , Dordrecht: Reidel. doi:10.1007/978-94-010-2175-3
• –––, 1977, “Randomness and the Right Reference Class”, Journal of Philosophy , 74(9): 501–520. doi:10.2307/2025794
• –––, 1978, “An Interpolation Theorem for Inductive Relations”, Journal of Philosophy , 75:93–98.
• –––, 2006, “Belief, Evidence, and Conditioning”, Philosophy of Science , 73(1): 42–65. doi:10.1086/510174
• Lange, Marc, 1999, “Calibration and the Epistemological Role of Bayesian Conditionalization”, Journal of Philosophy , 96(6): 294–324. doi:10.2307/2564680
• –––, 2002, “Okasha on Inductive Scepticism”, The Philosophical Quarterly , 52(207): 226–232. doi:10.1111/1467-9213.00264
• Laudan, Larry, 1997, “How About Bust? Factoring Explanatory Power Back into Theory Evaluation”, Philosophy of Science , 64(2): 206–216. doi:10.1086/392553
• Lenhard Johannes, 2006, “Models and Statistical Inference: The Controversy Between Fisher and Neyman-Pearson”, British Journal for the Philosophy of Science , 57(1): 69–91. doi:10.1093/bjps/axi152
• Levi, Isaac, 1967, Gambling with Truth: An Essay on Induction and the Aims of Science , New York: Knopf.
• –––, 1977, “Direct Inference”, Journal of Philosophy , 74(1): 5–29. doi:10.2307/2025732
• –––, 1978, “Confirmational Conditionalization”, Journal of Philosophy , 75(12): 730–737. doi:10.2307/2025516
• –––, 1980, The Enterprise of Knowledge: An Essay on Knowledge, Credal Probability, and Chance , Cambridge, MA: MIT Press.
• Lewis, David, 1980, “A Subjectivist’s Guide to Objective Chance”, in Richard C. Jeffrey, (ed.), Studies in Inductive Logic and Probability , vol. 2, Berkeley: University of California Press, 263–293.
• Maher, Patrick, 1993, Betting on Theories , Cambridge: Cambridge University Press.
• –––, 1996, “Subjective and Objective Confirmation”, Philosophy of Science , 63(2): 149–174. doi:10.1086/289906
• –––, 1997, “Depragmatized Dutch Book Arguments”, Philosophy of Science , 64(2): 291–305. doi:10.1086/392552
• –––, 1999, “Inductive Logic and the Ravens Paradox”, Philosophy of Science , 66(1): 50–70. doi:10.1086/392676
• –––, 2004, “Probability Captures the Logic of Scientific Confirmation”, in Christopher Hitchcock (ed.), Contemporary Debates in Philosophy of Science , Oxford: Blackwell, 69–93.
• –––, 2005, “Confirmation Theory”, The Encyclopedia of Philosophy , 2nd edition, Donald M. Borchert (ed.), Detroit: Macmillan.
• –––, 2006a, “The Concept of Inductive Probability”, Erkenntnis , 65(2): 185–206. doi:10.1007/s10670-005-5087-5
• –––, 2006b, “A Conception of Inductive Logic”, Philosophy of Science , 73(5): 513–523. doi:10.1086/518321
• –––, 2010, “Bayesian Probability”, Synthese , 172(1): 119–127. doi:10.1007/s11229-009-9471-6
• Mayo, Deborah G., 1996, Error and the Growth of Experimental Knowledge , Chicago: University of Chicago Press.
• –––, 1997, “Duhem’s Problem, the Bayesian Way, and Error Statistics, or ‘What’s Belief Got to do with It?’”, Philosophy of Science , 64(2): 222–244. doi:10.1086/392549
• Mayo Deborah and Aris Spanos, 2006, “Severe Testing as a Basic Concept in a Neyman-Pearson Philosophy of Induction“, British Journal for the Philosophy of Science , 57(2): 323–357. doi:10.1093/bjps/axl003
• McGee, Vann, 1994, “Learning the Impossible”, in E. Eells and B. Skyrms (eds.), Probability and Conditionals: Belief Revision and Rational Decision , New York: Cambridge University Press, 179–200.
• McGrew, Timothy J., 2003, “Confirmation, Heuristics, and Explanatory Reasoning”, British Journal for the Philosophy of Science , 54: 553–567.
• McGrew, Lydia and Timothy McGrew, 2008, “Foundationalism, Probability, and Mutual Support”, Erkenntnis , 68(1): 55–77. doi:10.1007/s10670-007-9062-1
• Neyman, Jerzy and E.S. Pearson, 1967, Joint Statistical Papers , Cambridge: Cambridge University Press.
• Norton, John D., 2003, “A Material Theory of Induction”, Philosophy of Science , 70(4): 647–670. doi:10.1086/378858
• –––, 2007, “Probability Disassembled”, British Journal for the Philosophy of Science , 58(2): 141–171. doi:10.1093/bjps/axm009
• Okasha, Samir, 2001, “What Did Hume Really Show About Induction?”, The Philosophical Quarterly , 51(204): 307–327. doi:10.1111/1467-9213.00231
• Popper, Karl, 1968, The Logic of Scientific Discovery , 3 rd edition, London: Hutchinson.
• Quine, W.V., 1953, “Two Dogmas of Empiricism”, in From a Logical Point of View , New York: Harper Torchbooks. Routledge Encyclopedia of Philosophy, Version 1.0, London: Routledge
• Ramsey, F.P., 1926, “Truth and Probability”, in Foundations of Mathematics and other Essays , R.B. Braithwaite (ed.), Routledge & P. Kegan,1931, 156–198. Reprinted in Studies in Subjective Probability , H. Kyburg and H. Smokler (eds.), 2 nd ed., R.E. Krieger Publishing Company, 1980, 23–52. Reprinted in Philosophical Papers , D.H. Mellor (ed.), Cambridge: University Press, Cambridge, 1990,
• Reichenbach, Hans, 1938, Experience and Prediction: An Analysis of the Foundations and the Structure of Knowledge , Chicago: University of Chicago Press.
• Rényi, Alfred, 1970, Foundations of Probability , San Francisco, CA: Holden-Day.
• Rosenkrantz, R.D., 1981, Foundations and Applications of Inductive Probability , Atascadero, CA: Ridgeview Publishing.
• Roush, Sherrilyn , 2004, “Discussion Note: Positive Relevance Defended”, Philosophy of Science , 71(1): 110–116. doi:10.1086/381416
• –––, 2006, “Induction, Problem of”, Sarkar and Pfeifer 2006..
• –––, 2006, Tracking Truth: Knowledge, Evidence, and Science , Oxford: Oxford University Press.
• Royall, Richard M., 1997, Statistical Evidence: A Likelihood Paradigm , New York: Chapman & Hall/CRC.
• Salmon, Wesley C., 1966, The Foundations of Scientific Inference , Pittsburgh, PA: University of Pittsburgh Press.
• –––, 1975, “Confirmation and Relevance”, in H. Feigl and G. Maxwell (eds.), Induction, Probability, and Confirmation , (Minnesota Studies in the Philosophy of Science, 6), Minneapolis: University of Minnesota Press, 3–36.
• Sarkar, Sahotra and Jessica Pfeifer (eds.), 2006, The Philosophy of Science: An Encyclopedia , 2 volumes, New York: Routledge.
• Savage, Leonard J., 1954, The Foundations of Statistics , John Wiley (2nd ed., New York: Dover 1972).
• Savage, Leonard J., et al., 1962, The Foundations of Statistical Inference , London: Methuen.
• Schlesinger, George N., 1991, The Sweep of Probability , Notre Dame, IN: Notre Dame University Press.
• Seidenfeld, Teddy, 1978, “Direct Inference and Inverse Inference”, Journal of Philosophy , 75(12): 709–730. doi:10.2307/2025515
• –––, 1992, “R.A. Fisher’s Fiducial Argument and Bayes’ Theorem”, Statistical Science , 7(3): 358–368. doi:10.1214/ss/1177011232
• Shafer, Glenn, 1976, A Mathematical Theory of Evidence , Princeton, NJ: Princeton University Press.
• –––, 1990, “Perspectives on the Theory and Practice of Belief Functions”, International Journal of Approximate Reasoning , 4(5–6): 323–362. doi:10.1016/0888-613X(90)90012-Q
• Skyrms, Brian, 1984, Pragmatics and Empiricism , New Haven, CT: Yale University Press.
• –––, 1990, The Dynamics of Rational Deliberation , Cambridge, MA: Harvard University Press.
• –––, 2000, Choice and Chance: An Introduction to Inductive Logic , 4 th edition, Belmont, CA: Wadsworth, Inc.
• Sober, Elliott, 2002, “Bayesianism—Its Scope and Limits”, in Swinburne 2002: 21–38. doi:10.5871/bacad/9780197263419.003.0002
• Spohn, Wolfgang, 1988, “Ordinal Conditional Functions: A Dynamic Theory of Epistemic States”, in William L. Harper and Brian Skyrms (eds.), Causation in Decision, Belief Change, and Statistics , vol. 2, Dordrecht: Reidel, 105–134. doi:10.1007/978-94-009-2865-7_6
• Strevens, Michael, 2004, “Bayesian Confirmation Theory: Inductive Logic, or Mere Inductive Framework?” Synthese , 141(3): 365–379. doi:10.1023/B:SYNT.0000044991.73791.f7
• Suppes, Patrick, 2007, “Where do Bayesian Priors Come From?” Synthese , 156(3): 441–471. doi:10.1007/s11229-006-9133-x
• Swinburne, Richard, 2002, Bayes’ Theorem , Oxford: Oxford University Press. doi:10.5871/bacad/9780197263419.001.0001
• Talbot, W., 2001, “Bayesian Epistemology”, in the Stanford Encyclopedia of Philosophy , (Fall 2001 Edition), Edward N. Zalta (ed.), URL = < https://plato.stanford.edu/archives/fall2001/entries/epistemology-bayesian/ >
• Teller, Paul, 1976, “Conditionalization, Observation, and Change of Preference”, in Harper and Hooker 1976: 205–259. doi:10.1007/978-94-010-1853-1_9
• Van Fraassen, Bas C., 1983, “Calibration: A Frequency Justification for Personal Probability ”, in R.S. Cohen and L. Laudan (eds.), Physics, Philosophy, and Psychoanalysis: Essays in Honor of Adolf Grunbaum , Dordrecht: Reidel. doi:10.1007/978-94-009-7055-7_15
• Venn, John, 1876, The Logic of Chance , 2 nd ed., Macmillan and co; reprinted, New York, 1962.
• Vineberg, Susan, 2006, “Dutch Book Argument”, Sarkar and Pfeifer 2006..
• Vranas, Peter B.M., 2004, “Hempel’s Raven Paradox: A Lacuna in the Standard Bayesian Solution”, British Journal for the Philosophy of Science , 55(3): 545–560. doi:10.1093/bjps/55.3.545
• Weatherson, Brian, 1999, “Begging the Question and Bayesianism”, Studies in History and Philosophy of Science [Part A] , 30(4): 687–697. doi:10.1016/S0039-3681(99)00020-5
• Williamson, Jon, 2007, “Inductive Influence”, British Journal for Philosophy of Science , 58(4): 689–708. doi:10.1093/bjps/axm032
• Zadeh, Lotfi A., 1965, “Fuzzy Sets”, Information and Control , 8(3): 338–353. doi:10.1016/S0019-9958(65)90241-X
• –––, 1978, “Fuzzy Sets as a Basis for a Theory of Possibility”, Fuzzy Sets and Systems , vol. 1, 3–28.

How to cite this entry . Preview the PDF version of this entry at the Friends of the SEP Society . Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers , with links to its database.

• Confirmation and Induction . Really nice overview by Franz Huber in the Internet Encyclopedia of Philosophy .
• Inductive Logic , (in PDF), by Branden Fitelson, Philosophy of Science: An Encyclopedia , (J. Pfeifer and S. Sarkar, eds.), Routledge. An extensive encyclopedia article on inductive logic.
• Teaching Theory of Knowledge: Probability and Induction . A very extensive outline of issues in Probability and Induction, each topic accompanied by a list of relevant books and articles (without links), compiled by Brad Armendt and Martin Curd.
• Probabilistic Confirmation Theory and Bayesian Reasoning . An annotated bibliography of influential works compiled by Timothy McGrew.
• Bayesian Networks Without Tears , (in PDF), by Eugene Charniak (Computer Science and Cognitive Science, Brown University). An introductory article on Bayesian inference.
• Miscellany of Works on Probabilistic Thinking . A collection of on-line articles on Subjective Probability and probabilistic reasoning by Richard Jeffrey and by several other philosophers writing on related issues.
• Fitelson’s course on Confirmation Theory . Main page of Branden Fitelson’s course on Confirmation Theory. The Syllabus provides an extensive list of links to readings. The Notes, Handouts, & Links page has Fitelson’s weekly course notes and some links to useful internet resources on confirmation theory.
• Fitelson’s course on Probability and Induction . Main page of Branden Fitelson’s course on Probability and Induction. The Syllabus provides an extensive list of links to readings on the subject. The Notes & Handouts page has Fitelson’s powerpoint slides for each of his lectures and some links to handouts for the course. The Links page contains links to some useful internet resources.

Bayes’ Theorem | epistemology: Bayesian | probability, interpretations of

Acknowledgments

Thanks to Alan Hájek, Jim Joyce, and Edward Zalta for many valuable comments and suggestions. The editors and author also thank Greg Stokley and Philippe van Basshuysen for carefully reading an earlier version of the entry and identifying a number of typographical errors.

Copyright © 2018 by James Hawthorne < hawthorne @ ou . edu >

• Accessibility

Support SEP

Mirror sites.

View this site from another server:

• Info about mirror sites

The Stanford Encyclopedia of Philosophy is copyright © 2024 by The Metaphysics Research Lab , Department of Philosophy, Stanford University

Library of Congress Catalog Data: ISSN 1095-5054

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Part Six: Evaluating Inductive Logic

Chapter Thirteen: How to Think About Inductive Logic

The known is finite, the unknown infinite; intellectually we stand on an islet in the midst of an illimitable ocean of explicability. Our business in every generation is to reclaim a little more land, to add something to the extent and solidity of our possessions. —T. H. Huxley

Our instincts certainly cause us to believe that the sun will rise tomorrow, but we may be in no better a position than the chicken which unexpectedly has its neck wrung. —Bertrand Russell, The Problems of Philosophy

• Inductive Arguments
• Frequency Arguments

13.1 Inductive Arguments

Deductive logic, even at its best, can help us to see no more than truths that are already built into an argument’s premises. To use Huxley’s metaphor—it can help us to better understand the small island of knowledge that we find ourselves standing on, but only that island. It is by inductive logic that we can go beyond our premises, that we can expand the size of our island of knowledge by reclaiming land from the surrounding ocean of the unknown. In these chapters, we will cover the most common varieties of inductive arguments.

Most of our arguments have conclusions that go well beyond their premises. Consider these examples:

• Based on my experience of sunrises in the past, I believe that the sun will rise tomorrow—but even if I am right about my experience of the past, it is at least possible that I am wrong about what tomorrow will bring.
• Public opinion organizations interview only a thousand people, yet they draw conclusions about how millions of voters—not just the thousand interviewed—are likely to cast their votes. Even if their data are correct about the opinions of the thousand that were interviewed, they could be mistaken about the millions.
• A detective finds fingerprints, a motive, and an opportunity and concludes that the butler did it. But even if there is nothing wrong with her evidence, it is still possible that she is wrong about the butler.

These arguments are not deductive. Deductive arguments are those in which the premises are intended to make the conclusions certain. Rather, they are inductive arguments , which we define as arguments in which the premises are intended to make their conclusions merely probable. The aim for an inductive argument is not validity but inductive strength , meaning that the premises of the successful argument make the conclusion probable. And, while deductive arguments are either valid or invalid with no middle ground, inductive arguments may be judged as having various degrees of strength—ranging from no support to very weak to fairly strong to very strong.

The difference between induction and deduction has to do with standards for logical success. Put simply, the logical standards for inductive arguments are lower, but there are more of them. They are lower, since inductive arguments aim only for probability, not for certainty. But there are more of them, since in inductive arguments, like deductive arguments, the conclusion must fit the premises; but, unlike deductive arguments, the conclusion must also fit the total available evidence.

13.1.1 Inductive Arguments Aim for Probability, Not for Certainty

Suppose you get on the freeway only to realize that you’re going south when you meant to go north. You see an off-ramp ahead and wonder whether there is an on-ramp that would allow you to return to the freeway in the opposite direction. You reason as follows:

• Almost all freeway off-ramps are paired with on-ramps in the opposite direction
• The Firestone Boulevard exit is a freeway off-ramp.
• ∴ The Firestone Boulevard exit is paired with an on-ramp in the opposite direction.

It turns out that you are right, and your trip continues successfully. But, even assuming the truth of your premises, your argument does no better than make probable your conclusion. It surely doesn’t guarantee there will be an on-ramp, for it is possible that this off-ramp is among those not covered by the “almost all” of the first premise.

Another way of saying that the premises do not guarantee the conclusion is to say that the argument is invalid—that it is possible for an argument of this form to have true premises and a false conclusion. We can show this by using the now-familiar two step procedure for producing validity counterexamples. The first step, recall, is to extract the form that the argument apparently relies on; the off-ramp argument is apparently relying on this form:

• Almost all F are G.

The second step is to substitute for the variables to produce clearly true premises and a clearly false conclusion. That can readily be done, as follows:

• Almost all species of birds can fly.
• Penguins are a species of birds.
• ∴ Penguins can fly.

Both premises are clearly true. But the conclusion is clearly false. So the argument is shown to be invalid. It cannot provide certainty.

Validity counterexamples can be given for nearly any inductive argument, no matter how logically strong it is. But inductive arguments can no more be faulted for invalidity than can the fabled soprano Maria Callas be faulted for failure to be enshrined in the Country Music Hall of Fame. Inductive arguments aim to make their conclusions probable, and that is the standard against which they should be judged.

Recall the question posed in Chapter 10 as the best way to think about the logic of any argument: If the premises were true, would that make it reasonable to believe the conclusion ? With deductive arguments, it is certainty that makes it reasonable to believe the conclusion; but with inductive arguments, it is probability. It would be nice if we could always reason with certainty. But we have to reason with what we have. The off-ramp argument would have been valid if I had used the premise All freeway off-ramps are paired with on-ramps in the opposite direction, but it would also have been unsound, since the new premise would have certainly been false.

13.1.2 Inductive Arguments Must Fit with the Total Available Evidence

The standards for logical success in inductive arguments are lower. But, at the same time, there are more of them—there are twice as many. Deductive arguments must satisfy only one condition to be logical; they must exemplify some correct form—that is, they must satisfy the correct form condition . For deductive arguments, it must be a deductive form such as affirming the antecedent or the process of elimination. Inductive arguments must also satisfy the correct form condition—that is, they must exemplify some correct inductive form. In this chapter and in the following three, we will cover the four most common forms of inductive arguments:

• Frequency arguments
• Inductive generalizations
• Arguments from analogy
• Explanatory arguments

Once you become familiar with each of these forms, you will find it fairly simple to determine whether you have an inductive or a deductive argument and, when inductive, to determine whether the correct form condition is satisfied (it usually is). As we will see, inductive arguments that make formal mistakes, like deductive arguments that make formal mistakes, typically provide no support to their conclusions.

An inductive argument, however, can satisfy the correct form condition but at the same time be logically defective. This is because inductive arguments must also satisfy a second condition, the total evidence condition . For each inductive form we will cover a customized way of stating this condition. To express it, for now, in general terms, the condition requires that the conclusion fit appropriately with the total available evidence —that is, with all of the beliefs and experiences (i.e., the total evidence ) that you personally have (i.e., that are available to you). Do not confuse this condition with the requirement of true premises. The total evidence condition bears on logic and is evaluated on the assumption that the premises are true; that is, this condition is to be considered as part of the process of answering the question, “If the premises were true, would they make it reasonable for me to believe the conclusion?”

Inductive Arguments: Two Conditions for Logical Success

• Correct form condition —conclusion must fit the premises.
• Total evidence condition —conclusion must also fit the total available evidence. These vary with each form of induction.

Consider again the off-ramp argument:

Suppose this argument has occurred to you when you suddenly think, “Wait a minute—I made the same mistake last week, and when I took the Firestone exit then I was stranded—no way back onto the freeway in either direction.” You still believe that each of the two premises is true, but they clearly no longer make the conclusion probable. Why not? Because there is evidence available to you—your background belief about what you experienced last week—that undermines the conclusion. Even though the argument satisfies the correct form condition, it fails the total evidence condition and is thus, from a logical point of view, extremely weak.

13.1.3 Standard Evaluating Format

The same format should be used for evaluating inductive arguments as for deductive ones. By way of review, this is the format:

Standard Evaluating Format

Heading: EVALUATION

Subheading: TRUTH. For each premise, state whether you judge it to be true and provide your defense of that judgment.

Subheading: LOGIC. State whether you judge the logic to be successful and provide your defense of that judgment.

Subheading: SOUNDNESS. State whether you judge the argument to be sound; then, if and only if it is not sound, state whether this is owing to a problem with a premise or with the logic.

Subheading (optional): CONVERSATIONAL RELEVANCE. If and only if the argument is flawed in this way, state whether it commits the fallacy of begging the question or missing the point, and explain how.

As always, direct your evaluation to the reasonable objector over your shoulder. The only new wrinkle is this: under the subheading logic, in your defense of the evaluation always consider whether it satisfies the total evidence condition, and always include a clear defense of that evaluation.

13.2 Frequency Arguments

13.2.1 correct form for frequency arguments.

The off-ramp argument is a frequency argument, [1]  the simplest and most intuitive form of inductive argument. Such arguments attempt to show that a specific item has a property because that sort of thing usually does have the property—or that it does not have a property because that sort of thing usually does not. Because the form (like repetition, simplification, conjunction, and disjunction, as we have seen in preceding chapters) is so simple and intuitive, it is not often explicitly offered. But it does provide a useful starting place for introducing inductive arguments. A frequency argument typically takes either a positive or negative form. The positive form is this:

• n of F are G (where n is a frequency >.5 and <1, i.e., more than half but less than all).

This is the form of the off-ramp argument.

The negative form is this:

• n of F are G (where n is a frequency <.5 and >0, i.e., less than half but more than none).
• ∴ A is not G.

This would be the form of my argument if I had said, “Almost no off-ramps leave you without a way to get back onto the freeway. The Firestone Boulevard exit is an off-ramp, so it’s reasonable to think that it won’t leave me without a way to get back onto the freeway.”

The premise Almost all freeway off-ramps are paired with on-ramps in the opposite direction is a frequency statement [2] of the sort that is used in the Chapter 10 discussion of frequency probability. These statements take the form n of F are G. The variable n stands for some frequency, or proportion; it may be stated in ordinary language—as with “almost all” in this premise—or as a decimal, a fraction, or a percentage. (We will use the lowercase letters m and n as variables standing for frequencies.) F and G, as always, are predicate letters. In inductive arguments, the predicate in the F position is usually termed the population, while the predicate in the G position is usually termed the property. A frequency statement states that with a certain frequency ( n ), a certain population ( F ) has a certain property ( G ). Here are a few frequency statements:

Almost all marchers for Black Lives Matter are peaceful. One in twenty US adults now smoke e-cigarettes. 2% of the trumpet players in the top fifteen symphony orchestras are women. Over half of the population of Europe was wiped out by the Black Death.

Note that none of the following qualifies as a frequency statement:

Many marchers for Black Lives Matter are peaceful. Millions of US adults now smoke e-cigarettes. Two of the trumpet players in the top fifteen symphony orchestras are women. Some 45 million Europeans were wiped out by the Black Death.

The quantities expressed in the last four cases are not proportional; they provide no estimate of how the quantity relates to the total population.

Frequency arguments use a form that is very close to that of a familiar deductive argument—namely, the singular categorical argument of which the Socrates argument is our stock example. Universal categorical statements are frequency statements in which the frequency is either all or none, so All men are mortal does qualify as a frequency statement. But All men are mortal, Socrates is a man, so Socrates is mortal is deductive, not inductive, so we will not categorize it as a frequency argument. The frequency statement in a frequency argument, as noted in the two forms above, cannot express a proportion of 1 or 0 (i.e., of all or none), since we are defining frequency arguments as inductive, and universal statements would make them deductive. [3]

Note also that the frequency statement in a frequency argument (shown as the first premise in each of the preceding two typical forms) cannot be exactly .5. If it were .5, it would mean that exactly half of the things that are F are also G —but that the other half are not G, making it exactly as probable as not that A is G and thus giving no reason to believe one over the other. An argument with such a premise may still be categorized as a frequency argument, but as one that fails the correct form condition—and thus, that is logically unsuccessful.

There are other ways that frequency arguments can fail the correct form condition. Charlie Hough, a steady but not dominant knuckle-balling major league pitcher, was quoted in the sports pages as saying, “They say most good managers were mediocre players. I should be a helluva manager.” His argument seems to be best clarified as follows:

• Most good managers were mediocre players.
• [Charlie Hough was a mediocre player.]
• ∴ Charlie Hough will be a good manager.

Its form is this:

• Most F are G.

The F and G of premise 2 and the conclusion are reversed, creating a problem that is analogous to Chapter 11’s fallacy of singular affirming the consequent. This argument provides no support for the conclusion.

Inductive strength and deductive validity have this in common: if either sort of argument fails the correct form condition, it normally provides no support for its conclusion. But after this they part ways. For even if an inductive argument satisfies the correct form condition, how strong it is remains an open question. How that question is to be closed is determined by how well the argument satisfies the total evidence condition—to which we now turn.

Exercises Chapter 13, set (a)

Clarify each of the passages below as a frequency argument; state whether it satisfies the correct form condition and, if not, explain.

Sample exercise.   I’m counting on good weather tomorrow; after all, it was rainy today, and at least half the time around here, clear days follow rainy ones.

Sample answer.

• .50 of days after rainy days are clear.
• Tomorrow is a rainy day after a clear day.
• ∴ Tomorrow will be clear.

Not correct form for frequency argument; frequency must be greater than .5 if it is to provide any support for the conclusion.

• Woman to her friend: Nine times out of ten, guys that I meet on a dating app are a big disappointment. I don’t expect to have a good time tonight
• Many reports on that site are unfounded conspiracy theories. I wouldn’t believe it if I were you.
• One fisherman to another: Oops—your tackle is snagged on the bottom of the lake. When that happens, more often than not it won’t come loose.. You might as well just cut your line and be done with it.
• Professor to class: Students remember about 80 percent of what they both see and hear. I am providing a handout to go with today’s lecture; therefore, I will expect you to remember this material.
• Most French painters late in the 19th century were impressionists. Seurat is an impressionist, so chances are he was a late 19th century French painter.

Correct Form for Frequency Arguments

Positive form:

• n of F are G ( n is a frequency >.5 and <1).

Negative form:

• n of F are G ( n is a frequency <.5 and >0).

13.2.2 The Total Evidence Condition (1): How High the Frequency Is

For frequency arguments, there are typically two simple components to the total evidence condition: first, the closer the frequency is to 1 or 0, the stronger the argument can be; and second, there must not be strong background evidence against the conclusion.

Total Evidence Condition for Frequency Arguments

• The closer the frequency is to 1 or 0, the stronger the argument can be.
• There must not be strong undermining evidence.

First, you should consider how high the frequency is. For the positive form of the argument the closer the frequency is to 1, the stronger the argument can be. This establishes a ceiling for the argument’s logical strength. The argument’s logic, for example, can never be judged as stronger than extremely weak if the frequency is a mere .51. It can ultimately be judged as weaker than that, however, since failure to satisfy the second part of the total evidence condition would offset anything gained by this first part. The negative form of frequency argument is the mirror image of the positive. The weakest arguments are just under .5, and the closer to 0 the stronger they can be.

You should be especially careful when evaluating colloquial terms on this criterion. Most, for example, is quite vague—ranging from just over half to practically all. If you are stuck with such a term, it is usually best not to assume that it moves you any more than halfway from .5 to 1—that is, that it represents anything greater than a .75 frequency. So a frequency argument with most cannot usually be judged as any better than “moderately strong.”

Exercises Chapter 13, set (b)

For each argument, give a preliminary judgment of each argument’s strength based solely on the first part of the total evidence condition. (These are the same as set (a), except for some small revisions to ensure that all of them satisfy the correct form condition.)

Sample exercise.  I’m counting on good weather tomorrow; after all, it was rainy today, and a little more than half the time around here, clear days follow rainy ones.

Sample answer. Very weak.

• Woman to her friend: Nine times out of ten, guys that I meet on a dating app are a big disappointment. I don’t expect to have a good time tonight.
• The vast majority of reports on that site are unfounded conspiracy theories. I wouldn’t believe it if I were you.
• Most French painters late in the 19th century were impressionists. Seurat is a late 19th century French painter, so chances are he was an impressionist.

13.2.3 The Total Evidence Condition (2): No Strong Undermining Evidence

In addition, there must not be strong undermining evidence—that is, strong background evidence against the conclusion. You must carefully consider whether you know anything else about A that would undermine the argument. This is exactly what happened in our revised version of the off-ramp argument. You reflected on your total evidence, remembered that you had already discovered that this exit was an exception—that is, that it allowed no way of getting back onto the freeway—and so you discounted the initial argument without further ado.

There is a more careful way of stating this part of the total evidence condition for frequency arguments. It is slightly more complicated, but is worth introducing because it will in some cases be helpful. You should consider whether there are other populations to which A belongs that weaken the initial support provided by the argument . Return once again to the off-ramp argument; the Firestone exit, according to the second premise, belongs to the population of freeway off-ramps. But when you reflect on your total evidence, you realize it also belongs to the population of things that you vividly remember as not having an opposing on-ramp. When expressed in this way, it may at first look as though you are in an evaluative logjam. On the one hand, almost all freeway on-ramps do provide an opposing return to the freeway; on the other hand, almost all things that you vividly remember are true. The frequency is about the same in each of the statements, yet one of them points to the truth of the conclusion while the other points to its falsity. It is intuitively clear that the second frequency statement wins—that is, that you are right to trust your memory. Why?

A simple, general procedure provides the solution. When you recognize the undermining evidence, you should consider yet another population, namely, the population that is made up of items belonging to both of the populations in question, and ask with what frequency this new population has the property in question. In the current case, the new, combined population is freeway off-ramps (original population) that you vividly remember as not being paired with opposing on-ramps (undermining population). With what frequency are members of this population likely to still have the property of being paired with an on-ramp in the opposite direction ? Almost never. The argument does not satisfy the second part of total evidence condition. The logic portion of your evaluation would look something like this:

The logic of the argument is extremely weak. The argument does satisfy the correct form condition for a frequency argument, but does not satisfy the total evidence condition. Although the frequency (“almost all”) is high enough, I remember that there is no opposing on-ramp for this off-ramp, and my memories of this sort of thing are almost always accurate.

One more example may prove useful. Suppose you are looking for a friend to join you for a skiing trip, and you want to be sure that you do not end up with a partner who will spend the whole time on the bunny slopes. You consider your Irish friend, Joseph Vaughan, but then reason as follows:

• Less than 1 percent of the residents of Ireland are experienced downhill skiers.
• Joseph Vaughan is a resident of Ireland.
• ∴ Joseph Vaughan is not an experienced downhill skier.

This is a frequency argument of the second, negative form. The form is correct and the frequency is extremely low, so, at first glance, you might expect to evaluate it as inductively strong. But then you must ask whether there is any undermining evidence that you know of—that is, whether Vaughan belongs to any populations in which the frequency of experienced downhill skiers is high. To make it easy, suppose you know that he is a former member of an Olympic downhill skiing team. With what frequency are members of both populations—residents of Ireland who have been Olympic downhill skiers—experienced skiers? Always. Your evaluation of the logic of the argument would look something like this:

The logic is extremely weak. The argument does satisfy the correct form condition for a frequency argument, but does not satisfy the total evidence condition. Though the frequency (under 1 percent) is low enough, Vaughan is a former Olympic skier, and no Olympic skier, even if from Ireland, is inexperienced at skiing.

Exercises Chapter 13, set (c)

Evaluate the logic of each of these frequency arguments, considering the background evidence in parentheses.

Sample exercise. I’m counting on good weather tomorrow; after all, it was rainy today, and a little more than half the time around here, clear days follow rainy ones. (You just saw a newscast that reported that the hurricane brewing over the Atlantic will hit your coastal town during the night.)

Sample answer. The logic of this argument is no good—the premises provide no support for the conclusion. It does satisfy the correct form condition, but the meager “more than half” frequency is more than offset by the likelihood that the newscaster was reliably reporting a very high probability of disastrous weather.

• Woman to her friend: Nine times out of ten, guys that I meet on a dating app are a big disappointment. I don’t expect to have a good time tonight. (Suppose your friend tells you that she knows him well and he’s
• The vast majority of reports on that site are unfounded conspiracy theories. I wouldn’t believe it if I were you. (Suppose you don’t have any other relevant background beliefs or experiences.)
• One fisherman to another: Oops—your tackle is snagged on the bottom of the lake. When that happens, more often than not it won’t come loose. You might as well just cut your line and be done with it. (Suppose you know that you are using super-lightweight line and you can see that you’ve gotten the tackle caught under a big rock.)
• Professor to class: Students remember about 80 percent of what they both see and hear. I am providing a handout to go with today’s lecture; therefore, I will expect you to remember this material. (Suppose the professor is exceptionally boring and the handout is confusing.)
• Most French painters late in the 19th century were impressionists. Seurat was a late 19th century French painter, so chances are he was an impressionist. (Suppose you’ve recently been to an exhibit of his work and you know that he was an impressionist.)

13.3.4 Arguments that Appeal to Authority

Arguments that appeal to authority can often best be understood as frequency arguments. In a text called Thinking Better, by David Lewis and James Greene, we are told this:

Ulrich Neisser, one of the world’s foremost specialists in the field of mental functioning, sets the record straight when he explains: “Human cognitive activity would be more usefully conceived of as a collection of acquired skills than as the operation of a single, fixed mechanism.” In other words, “intelligence” is something we acquire from experience rather than an inborn ability.

The authors are telling us, apparently, that because an expert such as Neisser supports their conclusion, we should accept it. This can be clarified as an argument in which the claim that Neisser is an expert on the relevant subject is charitably paraphrased as a frequency statement.

• Most of what Ulrich Neisser says about mental functioning is true.
• That intelligence is not innate is something that Ulrich Neisser says about mental functioning.
• ∴ That intelligence is not innate is true.

It is particularly important that you be careful when you specify the population in these sorts of arguments. It is most charitable to suppose that the argument is not depending on the implicit supposition that most of what Neisser says is true, but that most of what Neisser says about mental functioning is true. It is most charitable because a premise that declared Neisser to be an expert in everything would be almost certainly false, while a premise that declared him to be an expert in this particular arena would likely be true.

What can be said about the logic of the argument? It does have correct form for a frequency argument. As for the total evidence condition, the argument is prevented from being any more than moderately strong since the frequency is expressed merely as “most.” But is there undermining evidence? Yes, because even the experts disagree sharply on this question. Some, such as Neisser, believe that intelligence is not innate; many others, however, are persuaded that it is largely innate. If this information is all you have to go on, the next thing to determine is the frequency with which any statement is true when the experts disagree about its truth. (That is, the next thing to determine is the frequency with which a statement is true when it belongs to the population that includes both the things that one set of experts says are true and the things that another set of experts says are false). This frequency is half the time. So it turns out that the argument is logically impotent. The premises, if true, provide no more reason to believe the conclusion than to disbelieve it, given the total evidence condition. (When evaluating appeals to authority that are represented as frequency arguments, it can be very useful to review the discussion of appeals to authority in Chapters 8 and 9.)

Exercises Chapter 13, set (d)

Clarify and evaluate each of these appeals to authority as frequency arguments.

Sample exercise. “An author of this book remarked after walking about the principality of Monaco, ‘Just think—only eight square miles!’ ‘I don’t see how you even get eight out of it,’ his brother replied. Yet the Encyclopaedia Britannica, the World Almanac, Scott’s stamp album, various American atlases, and the gazetteers in the dictionaries had agreed on eight square miles.” —Quine and Ullian, The Web of Belief  (The book then provides the following additional information that can be useful background for evaluating the quality of the argument from authority above. On further investigation, the author found that the 11th edition of the Encyclopaedia Britannica, from the early 20th century, had made a mistake in arithmetic, stating: “Area about 8 square miles, the length being 2 miles and the width varying from 500 to 1,800 yards.” Apparently all of the reference works, which were later, had simply copied the Britannica’s mistaken “8 square miles.”)

• [Almost all of the statements about geography found in the Britannica, the World Almanac, Scott’s stamp album, various American atlases, and the gazetteers in the dictionaries are true.]
• That Monaco is eight square miles is a statement about geography found in all of these sources.
• ∴ That Monaco is eight square miles is true.

Premise 1 is probably true; theses sources depend on extensive careful research and are, in general, abundantly confirmed by the experience of their users.

Premise 2 is probably true; there is no reason to doubt the reliability of Quine and Ullian; the statements are not so improbable that I would not be willing to take their word for it; and I checked some of the older sources just to make sure, and they do make this claim.

Extremely weak, given the background information provided above. It is in the correct form for frequency argument, and the frequency is high enough for it to be strong. But the doubts of the passage’s author, combined with his success in tracking down the source of the mistake in a mathematical error committed by the Britannica, leave the argument failing to fit the total evidence condition.

The argument is unsound, because the argument is logically weak.

• I should think that Hoda Kotb knows what she’s talking about if she reports on the news that America has struck at terrorist bases in the Middle East. So, yes, I do have good reason to believe we are fighting back against terrorism.
• The fire in the abandoned oil well got so bad that city officials consulted with Red Adair, the legendary fireman of the oil fields. “You’re not going to kill that fire with conventional methods,” said Adair. “The first thing I would try is explosives.” (Suppose a city official argues that Adair should be trusted, due to his expertise in this area.)
• “A scholar meeting a person, said to him, ‘I heard you were dead.’ To which the other answered, ‘You see I am alive.’ The scholar replied, ‘Perhaps so, but he who told me was a man of much more credit than you.’” —Robert O. Foote, “Who Was Joe Miller?” (Clarify and evaluate the scholar’s argument, again as an appeal to authority that can be taken as a frequency argument.)
• “Seven years of largely unrecognized and unrewarded effort have led a mathematician to solve one of the most famous problems in mathematics. Until Louis de Branges of Purdue University recently proved that it was true, this problem, known as the Bierbach conjecture, had challenged mathematicians for almost 70 years. Last March, de Branges sent out his proof, as part of a 350-page manuscript for a book on power series, to about a dozen mathematicians so that the proof could be verified. ‘Every one of them wrote back and said that they would not be able to read it at the time,’ says de Branges. Explains U. of Mich. mathematician Peter Duren, one of the recipients of the manuscript, ‘We were frankly skeptical that he had done it. De Branges had a history of announcing proof of important theorems that turned out to be wrong. It has certainly shaken up the field.’”— Science News (Clarify Duren’s initial argument for thinking that de Branges was wrong. It provides an interesting twist on the ordinary appeals to authority. To simplify your evaluation, suppose you don’t have the information in the first part of the passage stating that the proof was successful.)

13.4 Summary of Chapter Thirteen

Inductive arguments differ from deductive ones in their standards for logical success. In both cases we ask whether true premises would make it reasonable for us to believe the conclusion. But, first, the standards for induction are lower. The aim of an inductive argument is for the premises to make the conclusion probable, while the aim of a deductive argument is for the premises to make the conclusion certain. Second, there are more standards for induction. Like deductive arguments, inductive ones must satisfy the correct form condition. But, unlike deductive arguments, they must also satisfy the total evidence condition. (The conclusion must not only fit the premises, but it must also fit the total available evidence.) There is a different version of this condition for each form of induction, and each will be introduced in the text in subsequent chapters. For now, you need only know that this condition requires that the conclusion accord with the total available evidence—that is, with all of the beliefs and experiences that you personally have.

Logical inductive arguments are not termed valid (they are in fact not valid, nor do they aspire to be so); rather, they are termed strong. And their success is a matter of degree, ranging from no support at all to very weak to fairly strong to very strong.

The simplest and most intuitive inductive form is the frequency argument. It always includes a frequency statement, which states that a specified population (say, dogs) has a certain property (say, being flea-ridden) with a certain frequency (say, 40 percent of the time). There are two parts to the total evidence condition for frequency arguments. First, the higher the frequency, the stronger the logic can be. (If the argument takes the form of denying that something has a property because the frequency in the population is so low, then the reverse holds and the lower the frequency, the stronger the argument.) And, second, you must not have any substantial undermining evidence among your background beliefs and experiences.

Appeals to authority are often aptly interpreted as frequency arguments, since they typically include an implicit premise to the effect that Most of what this expert says about this topic is true.

13.5 Guidelines for Chapter Thirteen

• When asking whether an inductive argument is logically successful, ask the same general question you ask of deductive arguments: If the premises were true, would that make it reasonable to believe the conclusion? In this case, however, expect only probability, not certainty.
• Inductive arguments must satisfy not only the correct form condition, but also the total evidence condition (that is, the conclusion must fit not only the premises, but also the total available evidence). This means that even if an inductive argument is formally correct, you can judge it to be a logical argument only if it also fits appropriately with your background beliefs and experiences.
• When evaluating inductive arguments, continue to follow the standard format for argument evaluation, but be sure to include in the logic section a discussion of the total evidence condition.
• Structure frequency arguments, when it would be loyal to do so, as follows: the first premise is a frequency statement about a property found in a population; the second premise identifies a member of the population; and the conclusion says whether this member has the property.
• In a frequency argument, the frequency establishes a ceiling for the argument’s logical strength. It cannot be higher, but it can be lower.
• When assessing the logic of a frequency argument, one way of considering whether there is undermining evidence is to ask whether A is a member of another population in which the frequency of those that do not have the property in question is high, and then to ask about the frequency of the property in the population of those who are members of both the first and the second population.
• When it is consistent with the principles of loyalty and charity, present arguments that appeal to authority as frequency arguments in which the frequency statement declares that most of what the authority says about a particular subject is true.

13.6 Glossary for Chapter Thirteen

Correct form condition —the logical requirement on any argument that it exemplify some correct form (that its conclusion fit with its premises). Correct deductive form is sufficient for deductive validity. But correct inductive form is sufficient for inductive strength if and only if it is paired with satisfaction of the total evidence condition.

Frequency argument —an inductive argument that takes one of these two forms:

These are also called statistical syllogisms , probabilistic syllogisms , myriokranic (that is, thousand-headed) syllogisms , and direct singular inferences .

Frequency statement —a statement of the following form: n of F are G. The variable n stands for some frequency, or proportion, stated in ordinary language (as with almost all ) or as a decimal, a fraction, or a percentage. The predicate in the F position is usually termed the population, while the predicate in the G position is usually termed the property. A frequency statement states that with a certain frequency ( n ), a certain population ( F ) has a certain property ( G ). Also called a simple statistical hypothesis.

Inductive argument —an argument in which the premises are intended to make the conclusion probable. Alternatively termed a probabilistic , ampliative , or nondemonstrative argument .

Inductive strength —the measure of an inductive argument’s logical success (contrast with deductive validity) based on how probable the premises make the conclusion. To be logically strong an inductive argument must satisfy both the correct form condition and the total evidence condition. There is a continuum of logical strength, ranging from no support at all to very weak to fairly strong to very strong.

Total available evidence —all of the beliefs and experiences (i.e., the total evidence ) that you as the evaluator personally have (i.e., that are available to you).

Total evidence condition —the logical requirement upon any inductive argument that its conclusion fit appropriately with the total available evidence. Do not confuse this condition with the requirement of true premises. The total evidence condition bears on logic and is evaluated on the assumption that the premises are true; that is, this condition is to be evaluated as part of answering the question If the premises were true, would they make it reasonable for me to believe the conclusion ?

• There is no generally accepted term for these arguments. They are also called proportional syllogisms, probabilistic syllogisms, myriokranic (i.e., thousand-headed) syllogisms, and direct singular inferences. ↵
• Sometimes termed a simple statistical hypothesis. ↵
• This is a boundary drawn solely for practical convenience, enabling us to say without qualification that frequency arguments are inductive arguments and that singular categorical arguments are deductive ones. ↵

An argument in which the premises are intended to make the conclusion probable. Alternatively termed a probabilistic , ampliative , or nondemonstrative argument .

The measure of an inductive argument’s logical success (contrast with deductive validity) based on how probable the premises make the conclusion. To be logically strong an inductive argument must satisfy both the correct form condition and the total evidence condition. There is a continuum of logical strength, ranging from no support at all to very weak to fairly strong to very strong.

The logical requirement on any argument that it exemplify some correct form (that its conclusion fit with its premises). Correct deductive form is sufficient for deductive validity. But correct inductive form is sufficient for inductive strength if and only if it is paired with satisfaction of the total evidence condition.

The logical requirement upon any inductive argument that its conclusion fit appropriately with the total available evidence. Do not confuse this condition with the requirement of true premises. The total evidence condition bears on logic and is evaluated on the assumption that the premises are true; that is, this condition is to be evaluated as part of answering the question If the premises were true, would they make it reasonable for me to believe the conclusion?

All of the beliefs and experiences (i.e., the total evidence ) that you as the evaluator personally have (i.e., that are available to you).

An inductive argument that takes one of these two forms:

1. n of F are G (where n is a frequency >.5 and <1, i.e., more than half but less than all). 2. A is F ∴ C .  A is G

1. n of F are G. (where n is a frequency <.5 and >0, i.e., less than half but more than none) 2. A is F. ∴ C .  A is not G

A statement of the following form: n of F are G. The variable n stands for some frequency, or proportion, stated in ordinary language (as with almost all ) or as a decimal, a fraction, or a percentage. The predicate in the F position is usually termed the population, while the predicate in the G position is usually termed the property. A frequency statement states that with a certain frequency ( n ), a certain population ( F ) has a certain property ( G ). Also called a simple statistical hypothesis.

A Guide to Good Reasoning: Cultivating Intellectual Virtues Copyright © 2020 by David Carl Wilson is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License , except where otherwise noted.

Share This Book

Deductive, Inductive, and Abductive Reasoning (with Examples)

Understanding different types of arguments is an important skill for philosophy as it enables us to assess the strength of the conclusions drawn. In this blog post, we’ll explore the characteristics of three different types of argument and look at some examples:

• Deductive arguments
• Inductive arguments
• Abductive arguments

Deductive Arguments: The Conclusion is Certainly True

Deductive arguments operate on the principle of logical necessity , aiming to provide conclusions that follow necessarily from the premises.

These arguments seek to establish the truth of specific claims based on the truth of general principles or premises. Deductive reasoning allows for definitive and conclusive outcomes if the premises are true.

In other words, deductive arguments are logically watertight: If the premises are true, it’s logically impossible for the conclusion to be false.

General Format of a Deductive Argument:

• Premise 1: General Principle A is true.
• Premise 2: General Principle B is true.
• Premise 3: General Principle C is true.
• Conclusion: Therefore, Specific Claim X is true.
• Premise 1: All dogs are mammals.
• Premise 2: Rex is a dog.
• Conclusion: Therefore, Rex is a mammal.

In this deductive argument, the conclusion follows necessarily from the premises. If we accept the truth of the general principle that all dogs are mammals (1) and the premise that Rex is a dog (2), we are logically compelled to accept the conclusion that Rex is a mammal (3).

Other examples of deductive argument formats include modus ponens and modus tollens .

Note: A deductively valid argument means the conclusion necessarily follows from the premises and so, if the premises of the argument are true, the conclusion must also be true. However, the premises may be false , in which case the conclusion may be false too. For example:

• Premise 1: If today is Monday, the moon is made of green cheese.
• Premise 2: Today is Monday.
• Conclusion: Therefore, the moon is made of green cheese.

This argument is still deductively valid – the conclusion does follow necessarily from the premises – but the conclusion is false because one or more of the premises are false . For more detail on valid reasoning (including the difference between a valid and sound argument) see this post .

Inductive Arguments: The Conclusion is Probably True

Inductive arguments involve reasoning from specific instances or observations to general conclusions or generalisations.

They aim to make general claims based on limited evidence, seeking to establish patterns, trends, or probabilities. While inductive arguments do not guarantee absolute certainty, they offer insights and probabilistic reasoning.

In other words, inductive arguments are not logically watertight – but they nevertheless provide support for the conclusion .

General Format of an Inductive Argument:

• Premise 1: Observation A is true.
• Premise 2: Observation B is true.
• Premise 3: Observation C is true.
• Conclusion: Therefore, it is likely that Generalisation X is true.
• Premise 1: Every bird I have observed can fly.
• Premise 2: The next bird I encounter will likely be able to fly.
• Premise 3: The bird species documented so far exhibit the ability to fly.
• Conclusion: Therefore, it is probable that all birds can fly.

This example illustrates an inductive argument where the conclusion is based on observed instances and generalises the ability of flight to all birds. While the conclusion is likely to be true, it is possible to encounter a bird species that cannot fly (e.g. an ostrich or a penguin), which weakens the argument’s strength.

Another type of inductive argument is an argument from analogy , where because two things are similar in one way they are likely to be similar in another way. For example, if your friend likes the same music as you, this may suggest they will like the same art as you.

Abductive Arguments: The Conclusion is the Best Explanation

Abductive arguments focus on finding the best or most plausible explanation for a given observation or phenomenon.

They involve reasoning from evidence to a hypothesis or explanation that provides the most likely account of the observed facts. An explanation may be considered more likely or plausible because it fits more neatly with the observed data, for example, or because it is the simplest explanation with the fewest assumptions (a principle known as Ockham’s Razor ).

Like inductive arguments, abductive arguments are not logically watertight. Although a hypothesis may seem to be the best explanation, other explanations are still logically possible.

General Format of an Abductive Argument:

• Observation: There is a certain observation or phenomenon.
• Evidence: Supporting evidence related to the observation.
• Hypothesis: A proposed explanation or claim that best accounts for the evidence.
• Conclusion: Therefore, Claim X is the most plausible explanation.
• Observation: The grass in the garden is wet.
• Evidence: There are water droplets on the leaves, and the ground is damp.
• Hypothesis: It rained last night.
• Conclusion: Therefore, the wet grass is most likely due to rain.

In this abductive argument, the wet grass and the presence of water droplets on the leaves and damp ground are the observed evidence. The hypothesis that it rained provides the best explanation for the observed evidence. However, other explanations, such as sprinklers or a hose, are also possible.

Applied to A Level Philosophy

There are various examples of deductive arguments, inductive arguments, and abductive arguments in A level philosophy .

Examples of deductive arguments in A level philosophy:

• The logical problem of evil
• Ontological arguments (e.g. Anselm’s or Malcolm’s )
• Descartes’ trademark argument

Examples of inductive arguments in A level philosophy:

• The evidential problem of evil
• Hume’s teleological argument
• Mill’s response to the problem of other minds

Examples of abductive arguments in A level philosophy:

• Russell’s argument that the external world is the best hypothesis
• Swinburne’s teleological argument

Identifying whether an argument is deductive, inductive, or abductive is a great way to demonstrate detailed and precise knowledge of philosophy and pick up those AO1 marks .

Further, knowing the difference between these types of arguments can also be useful to help evaluate ( AO2 ) the strengths and weaknesses of the various arguments you consider in the 25 mark essay questions.

• Straightforward explanations of syllabus topics for all 4 modules
• Bullet point summaries at the end of each module
• Exam blueprint for each question type (with example answers)
• Essay 25 mark essay plans for every major topic
• Glossary of key terms

Deductive and Inductive Reasoning Essay

Inductive and deductive reasoning: essay introduction, deductive approach, inductive approach, inductive vs deductive: essay conclusion, reference list.

There are different types of reasoning, most of which are explained in psychology books and articles. This paper discusses two types of reasoning – deductive and inductive reasoning using cognitive research. The inductive and deductive reasoning essay you read focuses on teaching science and technical courses in High Schools. It explores cases of science and mathematical teaching in schools.

Deductive reasoning is a logical process where conclusions are made from general cases. General cases are studied, after which conclusions are made as they apply to a certain case (Byrne, Evans and Newstead, 2019). In the context of this deductive reasoning essay, an argument from analogy is one of the examples under deductive reasoning. The rule underlying this module is that in the case where P and Q are similar and have properties a, b, and c, object P has an extra property, “x.” Therefore, Q will automatically have the same extra property, “x,” as the two are similar (Dew Jr and Foreman, 2020).

Most high school students in the United States do come across the argument from the analogy model of deductive reasoning while studying science subjects. Nonetheless, most students do not realize the applicability of this rule. They apply the rule unconsciously. Therefore, high school students should learn about this model of reasoning. This will help them know certain instances under which they should apply this rule when making arguments in science subjects (National Academies of Sciences, Engineering, and Medicine, 2019).

Researches conducted on analogies give a clear way of explaining why student reports have added ideas. While studying scientific subjects, students do make productive analogies. They apply scientific principles, for instance, energy conservation principles, to different settings.

Unproductive analogies are also made by students, for example, in experiments between temperature and heat. Research that compares different forms of analogies gained from visual and animated representations. Such studies distinguish the functions of different brain parts. It emphasizes the benefits of activating correct pathways for specific learning forms. Research on analogies emphasizes on the selection and inclusion of right analogies in the reports. It also encourages the analysis of different analogies (Vygotsky, 2020).

Argument from analogy is one of the tools that students can use to advance reasonable arguments in different science subjects. This is according to a study that was conducted to ascertain the model that can be used by high school students in when solving problems in genetics. Different questions and student-teacher engagements were used to reach the conclusion (Choden and Kijkuakul, 2020).

The major problems in the teaching of science subjects are the lapses in communication. More often, students and teachers in science classrooms rarely share similar purpose on either the subject or the activity. At times, teachers and students assign different meanings to the same concept. This happens in cases where the two have different levels of understanding about the science concepts because most of these concepts are technical (Choden and Kijkuakul, 2020).

In order to improve the understanding of science subjects, students are required to use different approaches. For students to use analogy, they must have an understanding of the concept in question first. The concept is the most important thing as arguments derived from the subject will be concrete when the concept is well grasped.

More models should be used by science teachers in the science classes. The real nature of the models or analogs used for teaching are better understood when they are realistic. Analogs are forms of human interventions in learning. They should be used carefully as poor use may result in mal understanding of the real meaning. Analogs have an aspect of practicality which leaves images in the minds of students.

When used well, a constructive learning environment will be attained. Analogies should be used in a way that students can easily capture or map. Students should also be given room to make suggestions of improving the analogies used by their teachers. Imperfect analogies expose difficulties that arise in describing and explaining scientific ideas that are mostly of an abstract nature (Newton, 2022).

According to Oaksford and Chater (2020), inductive reasoning entails taking certain examples and using the examples to develop a general principle. It cannot be utilized in proving a concept. In inductive reasoning, solutions to problems can be reached even when the person offering the solution does not have general knowledge about the world.

An example of deductive reasoning is the case of ‘Rex the dog’. In this case, a child can make a deduction that is logical when Rex barks even at times when barking itself is an unfamiliar activity. If the child was told that Rex is a cat and that all cats bark, the child would respond with a “yes” when asked whether Rex barks. This is even when Rex does not bark. Under this reasoning, logical deductions are counterfactual in that they are not made in line with the beliefs of the real world (Pellegrino and Glaser, 2021).

On the other hand, inductive reasoning is one of the oldest learning models. Inductive reasoning develops with time as students grow. However, this reasoning has not been fully utilized in schools. It carries many cognitive skills within it. Inductive thinking is used in creative arts in high schools. In creative art subjects, students are expected to build on their learned ideas. The knowledge learned is applied in different contexts. This is the real goal of inductive reasoning (Csapó, 2020).

For the purposes of the inductive reasoning essay, research has revealed that deductive reasoning can be applied in two performance contexts. This includes the school knowledge application and the applicable knowledge context. School knowledge is the knowledge that is acquired at school. This knowledge is mostly applied in situations that are related to schoolwork.

It is applied in a similar context in which it was acquired. This knowledge or reasoning is what the students apply in handling assignments, tests, and examinations in school. It is used to grade students and determine student careers in schools. Applicable knowledge can be easily applied in situations that differ from the context in which the command was acquired (Csapó, 2020).

Research conducted in the United States revealed that the skills students acquire at the elementary level are insufficient. Elementary mathematics teaching lacks a conceptual explanation to the students. When these students get to high school, they need a basis upon which they can understand mathematical formulas and measurements. Therefore, teachers are forced to introduce these students to a higher level of thinking.

The tasks in high school mathematics that require deep thinking are also called high cognitive demand tasks. At this level of thinking, students can understand complex mathematical concepts and apply them correctly. Thus, students are introduced to inductive reasoning (Brahier, 2020).

Students will mostly have a tough time at the introductory to inductive reasoning. Students will get a grasp of concepts, mostly mathematical ones. However, it will take longer for students to develop application skills. Mathematical concepts will be understood by students within a short span.

However, applying the concepts to solve different mathematical problems is another problem. Just like for the two types of knowledge, it has always been hard for students from high school to apply the school concept in the real world. Students acquire the inside, but in most cases, they reserve it for schoolwork only.

When students do not get good tutoring, gaining the transition required to achieve the real concepts becomes difficult. This idea further destroys them and may even cause a total failure to understand and apply inductive reasoning (Van Vo and Csapó, 2022).

The transition from elementary school to high school includes psychological changes. These changes need to be molded by introducing the student to detailed thinking. This gradual process begins with slowly ushering the students to simple concepts. This simple concept builds slowly, and complexity is introduced gradually.

The students’ minds grow as they get used to the hard concepts. Later, the students become more creative and critical in thinking and understanding concepts (Hayes et al., 2019).

Inductive and deductive reasoning are two types of reasoning that borrow from one another. The use of logical conclusion applies in both of them. They are very useful, especially in teaching mathematics and science courses.

Brahier, D. (2020) Teaching secondary and middle school mathematics . Abingdon: Routledge.

Byrne, R.M., Evans, J.S.B. and Newstead, S.E. (2019) Human reasoning: the psychology of deduction . London: Psychology Press.

Choden, T. and Kijkuakul, S. (2020) ‘Blending problem based learning with scientific argumentation to enhance students’ understanding of basic genetics’, International Journal of Instruction , 13(1), pp. 445-462.

Csapó, B. (2020) ‘Development of inductive reasoning in students across school grade levels’, Thinking Skills and Creativity , 37, pp. 1-15.

Dew Jr, J.K. and Foreman, M.W. (2020) How do we know?: an introduction to epistemology . Westmont: InterVarsity Press.

Hayes, B.K. et al. (2019) ‘The diversity effect in inductive reasoning depends on sampling assumptions’, Psychonomic Bulletin & Review , 26, pp.1043-1050.

National Academies of Sciences, Engineering, and Medicine (2019) Science and engineering for grades 6-12: investigation and design at the center . Washington, D.C.: National Academies Press.

Newton, D.P. (2022) A practical guide to teaching science in the secondary school . Milton Park: Taylor & Francis.

Oaksford, M. and Chater, N. (2020) ‘New paradigms in the psychology of reasoning’, Annual Review of Psychology , 71, pp. 305-330.

Pellegrino, J.W. and Glaser, R. (2021) ‘Components of inductive reasoning’, In Aptitude, learning, and instruction (pp. 177-218). Abingdon: Routledge.

Upmeier zu Belzen, A., Engelschalt, P. and Krüger, D. (2021) ‘Modeling as scientific reasoning – the role of abductive reasoning for modeling competence’, Education Sciences , 11(9), pp. 1-11.

Van Vo, D. and Csapó, B. (2022) ‘Exploring students’ science motivation across grade levels and the role of inductive reasoning in science motivation’, European Journal of Psychology of Education , 37(3), pp. 807-829.

Vygotsky, L.S. (2020) Educational psychology . Boca Raton: CRC Press.

• Chicago (A-D)
• Chicago (N-B)

IvyPanda. (2024, February 3). Deductive and Inductive Reasoning. https://ivypanda.com/essays/deductive-and-inductive-reasoning-essay/

"Deductive and Inductive Reasoning." IvyPanda , 3 Feb. 2024, ivypanda.com/essays/deductive-and-inductive-reasoning-essay/.

IvyPanda . (2024) 'Deductive and Inductive Reasoning'. 3 February.

IvyPanda . 2024. "Deductive and Inductive Reasoning." February 3, 2024. https://ivypanda.com/essays/deductive-and-inductive-reasoning-essay/.

1. IvyPanda . "Deductive and Inductive Reasoning." February 3, 2024. https://ivypanda.com/essays/deductive-and-inductive-reasoning-essay/.

Bibliography

IvyPanda . "Deductive and Inductive Reasoning." February 3, 2024. https://ivypanda.com/essays/deductive-and-inductive-reasoning-essay/.

• Inductive Versus Deductive Profiling
• Deductive vs. Inductive Reasoning in Everyday Life
• Deductive Reasoning: Social Contract Algorithm
• Inductive and Deductive Approach in Social Science
• Deductive and Inductive Arguments in Medical Profession
• Inductive and Deductive Criminal Profiling Methodologies
• Market Research: Inductive and Deductive Models
• A Logical Error Is Called a Logical Fallacy
• Thinking Types and Problem Identification
• Cognitive Processes in Problem Solving
• Contemporary Mathematical Model of Human Behavior Under Some Environmental Constraints
• An Early Literacy Intervention
• Biological Psychology
• The Mind Is Separate From the Brain: A Descartes’ Assumptions
• Value Neutrality for a counselor