hypothesis test example questions

Data Science Duniya

Learn Data Science, Machine Learning and Artificial Intelligence

Practice Problems on Hypothesis Testing

In this post I have put together the practice problems (from my academics study notes) to explain how in practical Hypothesis Testing works. This post is written mostly for the learners who want to deep dive into the statistics for data science. Focus will be on problem solving. For concepts please refer my previous posts on testing of hypothesis.

Prerequisite to understand Hypothesis testing examples:

• Understanding of hypothesis testing concepts
• How to use z-table, t-table and chi square table.

Formula list:

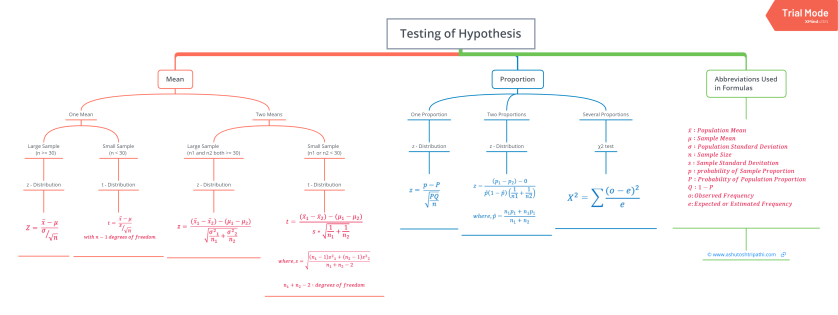
Critical Regions

In hypothesis testing, critical region is represented by set of values, where null hypothesis is rejected. So it is also know as region of rejection. It takes different boundary values for different level of significance. Below info graphics shows the region of rejection that is critical region and region of acceptance with respect to the level of significance 1%.

A Telecom service provider claims that individual customers pay on an average 400 rs. per month with standard deviation of 25 rs. A random sample of 50 customers bills during a given month is taken with a mean of 250 and standard deviation of 15. What to say with respect to the claim made by the service provider?

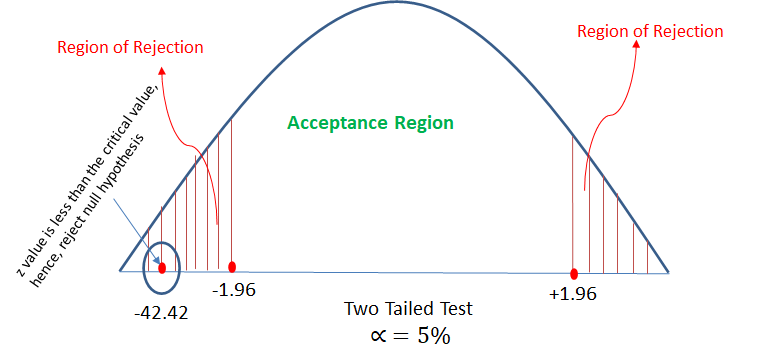
From the data available, it is observed that 400 out of 850 customers purchased the groceries online. Can we say that most of the customers are moving towards online shopping even for groceries?

It is found that 250 errors in the randomly selected 1000 lines of code from Team A and 300 errors in 800 lines of code from Team B. Can we assume that team B’s performance is superior to that of A.

Following is the record of number of accidents took place during the various days of the week.

Can we conclude that accident s are independent of the day of week?

Analyze the below data and tell whether you can conclude that smoking causes cancer or not?

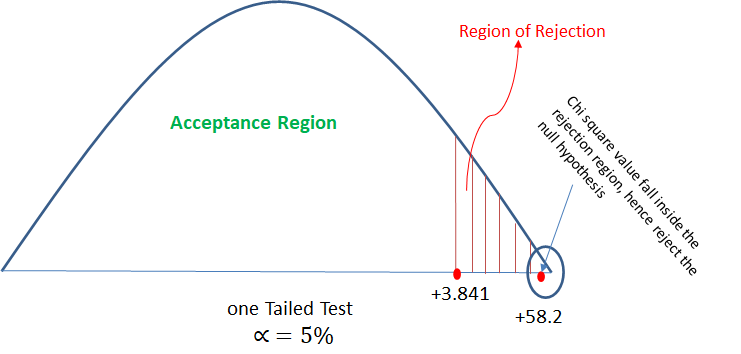
It is claimed that the mean of the population is 67 at 5% level of significance. Mean obtained from a random sample of size 100 is 64 with SD 3. Validate the claim.

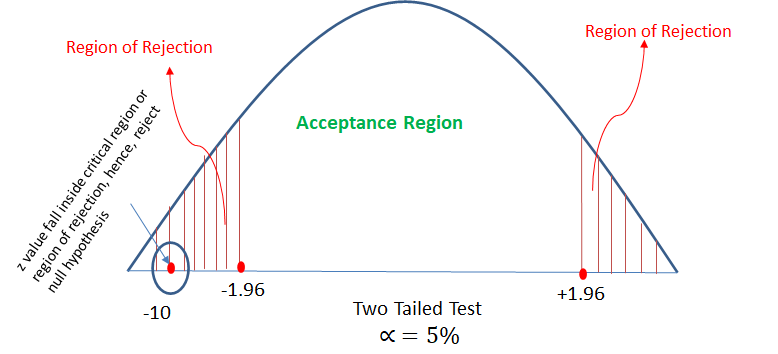
There is an assumption that there is no significant difference between boys and girls with respect to intelligence. Tests are conducted on two groups and the following are the observations

Validate the claim with 5% LoS (Level of Significance)

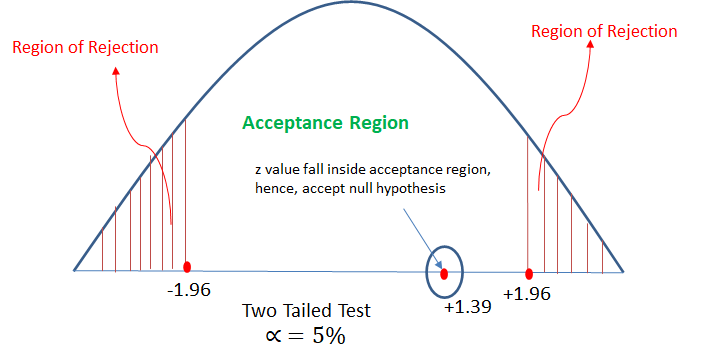
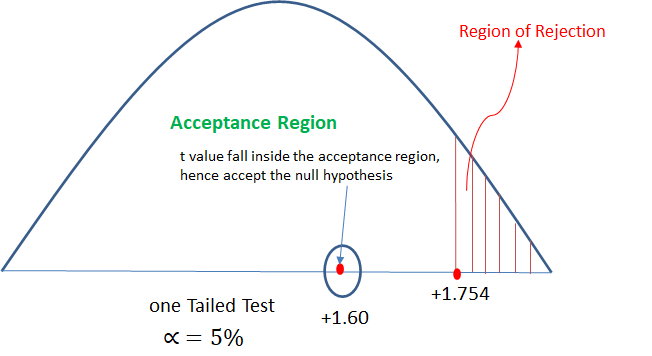
An automobile tyre manufacturer claims that the average life of a particular grade of tyre is more than 20,000 km. A random sample of 16 tyres is having mean 22,000 km with a standard deviation of 5000 km.

Validate the claim of the manufacturer at 5% LoS.

That is all for now. Please share your thoughts using the comment section below.

Type your email…

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)
• Click to print (Opens in new window)
• Click to email a link to a friend (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on Reddit (Opens in new window)
• Click to share on WhatsApp (Opens in new window)
• Click to share on Tumblr (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to share on Pocket (Opens in new window)
• Click to share on Telegram (Opens in new window)

Solution to question #2 is wrong because the value of Step 1: calculate z value using the z-test formula z = (p – P)/√(P*Q/n) z = (0.47 – 0.50)/√(0.5*0.5/850) z = 1.74 should be negative value. So in the conclusion you should be comparing -1.64 vs -1.74 and since -1.74 falls under the rejection region, you should be rejecting the null hypnosis

Thank you Karan. solution is updated.

I think smoking problem is wrongly concluded. There the H0 is assumed of dependency(smoking and cancer are dependent) while for chi square test, the null hypothesis is always for independence. So the H0 should be “Smoking and Cancer are independent”.

Please how can I download this page?

In the last sum the alternate hypothesis is less than 22,000 and the null hypothesis is more than 20,000. If the value turns out to be 21,000 then which hypothesis will you accept? I guess there’s an error, the alternate hypothesis should be less than equal to 20,000 and not 22,000. Correct me if I’m wrong.

Thanks for presenting above test cases, it really really helps to understand the tail concept. I am reading z-test and refer your hypothesis page as an example. I go through z-test example and in example no.8 last one it is “One tail – Left tailed test” but in the diag below it shows the right tailed. Not sure am I interpret wrong or diag error ? pls . correct me. Thanks.

The alternate hypothesis is the opposite of null hypothesis so it’s less less than or left tailed. Since the null hypothesis was accepted the graph is Right Tailed had the null hypothesis been rejected or the alternate hypothesis been accepted the graph would have been left tailed. I hope I cleared your doubt

Leave a Reply Cancel reply

This site uses Akismet to reduce spam. Learn how your comment data is processed .

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar