do hypothesis need to be tested

• Search Search Please fill out this field.
• Fundamental Analysis

Hypothesis to Be Tested: Definition and 4 Steps for Testing with Example

What Is Hypothesis Testing?

Hypothesis testing, sometimes called significance testing, is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used and the reason for the analysis.

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data. Such data may come from a larger population, or from a data-generating process. The word "population" will be used for both of these cases in the following descriptions.

Key Takeaways

• Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data.
• The test provides evidence concerning the plausibility of the hypothesis, given the data.
• Statistical analysts test a hypothesis by measuring and examining a random sample of the population being analyzed.
• The four steps of hypothesis testing include stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

How Hypothesis Testing Works

In hypothesis testing, an  analyst  tests a statistical sample, with the goal of providing evidence on the plausibility of the null hypothesis.

Statistical analysts test a hypothesis by measuring and examining a random sample of the population being analyzed. All analysts use a random population sample to test two different hypotheses: the null hypothesis and the alternative hypothesis.

The null hypothesis is usually a hypothesis of equality between population parameters; e.g., a null hypothesis may state that the population mean return is equal to zero. The alternative hypothesis is effectively the opposite of a null hypothesis (e.g., the population mean return is not equal to zero). Thus, they are mutually exclusive , and only one can be true. However, one of the two hypotheses will always be true.

The null hypothesis is a statement about a population parameter, such as the population mean, that is assumed to be true.

4 Steps of Hypothesis Testing

All hypotheses are tested using a four-step process:

• The first step is for the analyst to state the hypotheses.
• The second step is to formulate an analysis plan, which outlines how the data will be evaluated.
• The third step is to carry out the plan and analyze the sample data.
• The final step is to analyze the results and either reject the null hypothesis, or state that the null hypothesis is plausible, given the data.

Real-World Example of Hypothesis Testing

If, for example, a person wants to test that a penny has exactly a 50% chance of landing on heads, the null hypothesis would be that 50% is correct, and the alternative hypothesis would be that 50% is not correct.

Mathematically, the null hypothesis would be represented as Ho: P = 0.5. The alternative hypothesis would be denoted as "Ha" and be identical to the null hypothesis, except with the equal sign struck-through, meaning that it does not equal 50%.

A random sample of 100 coin flips is taken, and the null hypothesis is then tested. If it is found that the 100 coin flips were distributed as 40 heads and 60 tails, the analyst would assume that a penny does not have a 50% chance of landing on heads and would reject the null hypothesis and accept the alternative hypothesis.

If, on the other hand, there were 48 heads and 52 tails, then it is plausible that the coin could be fair and still produce such a result. In cases such as this where the null hypothesis is "accepted," the analyst states that the difference between the expected results (50 heads and 50 tails) and the observed results (48 heads and 52 tails) is "explainable by chance alone."

Some staticians attribute the first hypothesis tests to satirical writer John Arbuthnot in 1710, who studied male and female births in England after observing that in nearly every year, male births exceeded female births by a slight proportion. Arbuthnot calculated that the probability of this happening by chance was small, and therefore it was due to “divine providence.”

What is Hypothesis Testing?

Hypothesis testing refers to a process used by analysts to assess the plausibility of a hypothesis by using sample data. In hypothesis testing, statisticians formulate two hypotheses: the null hypothesis and the alternative hypothesis. A null hypothesis determines there is no difference between two groups or conditions, while the alternative hypothesis determines that there is a difference. Researchers evaluate the statistical significance of the test based on the probability that the null hypothesis is true.

What are the Four Key Steps Involved in Hypothesis Testing?

Hypothesis testing begins with an analyst stating two hypotheses, with only one that can be right. The analyst then formulates an analysis plan, which outlines how the data will be evaluated. Next, they move to the testing phase and analyze the sample data. Finally, the analyst analyzes the results and either rejects the null hypothesis or states that the null hypothesis is plausible, given the data.

What are the Benefits of Hypothesis Testing?

Hypothesis testing helps assess the accuracy of new ideas or theories by testing them against data. This allows researchers to determine whether the evidence supports their hypothesis, helping to avoid false claims and conclusions. Hypothesis testing also provides a framework for decision-making based on data rather than personal opinions or biases. By relying on statistical analysis, hypothesis testing helps to reduce the effects of chance and confounding variables, providing a robust framework for making informed conclusions.

What are the Limitations of Hypothesis Testing?

Hypothesis testing relies exclusively on data and doesn’t provide a comprehensive understanding of the subject being studied. Additionally, the accuracy of the results depends on the quality of the available data and the statistical methods used. Inaccurate data or inappropriate hypothesis formulation may lead to incorrect conclusions or failed tests. Hypothesis testing can also lead to errors, such as analysts either accepting or rejecting a null hypothesis when they shouldn’t have. These errors may result in false conclusions or missed opportunities to identify significant patterns or relationships in the data.

The Bottom Line

Hypothesis testing refers to a statistical process that helps researchers and/or analysts determine the reliability of a study. By using a well-formulated hypothesis and set of statistical tests, individuals or businesses can make inferences about the population that they are studying and draw conclusions based on the data presented. There are different types of hypothesis testing, each with their own set of rules and procedures. However, all hypothesis testing methods have the same four step process, which includes stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result. Hypothesis testing plays a vital part of the scientific process, helping to test assumptions and make better data-based decisions.

Sage. " Introduction to Hypothesis Testing. " Page 4.

Elder Research. " Who Invented the Null Hypothesis? "

Formplus. " Hypothesis Testing: Definition, Uses, Limitations and Examples. "

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

Methodology

• How to Write a Strong Hypothesis | Steps & Examples

How to Write a Strong Hypothesis | Steps & Examples

Published on May 6, 2022 by Shona McCombes . Revised on November 20, 2023.

A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses before you start your experiment or data collection .

Example: Hypothesis

Daily apple consumption leads to fewer doctor’s visits.

Table of contents

What is a hypothesis, developing a hypothesis (with example), hypothesis examples, other interesting articles, frequently asked questions about writing hypotheses.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess – it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Variables in hypotheses

Hypotheses propose a relationship between two or more types of variables .

• An independent variable is something the researcher changes or controls.
• A dependent variable is something the researcher observes and measures.

If there are any control variables , extraneous variables , or confounding variables , be sure to jot those down as you go to minimize the chances that research bias  will affect your results.

In this example, the independent variable is exposure to the sun – the assumed cause . The dependent variable is the level of happiness – the assumed effect .

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

Step 1. Ask a question

Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project.

Step 2. Do some preliminary research

Your initial answer to the question should be based on what is already known about the topic. Look for theories and previous studies to help you form educated assumptions about what your research will find.

At this stage, you might construct a conceptual framework to ensure that you’re embarking on a relevant topic . This can also help you identify which variables you will study and what you think the relationships are between them. Sometimes, you’ll have to operationalize more complex constructs.

Step 3. Formulate your hypothesis

Now you should have some idea of what you expect to find. Write your initial answer to the question in a clear, concise sentence.

4. Refine your hypothesis

You need to make sure your hypothesis is specific and testable. There are various ways of phrasing a hypothesis, but all the terms you use should have clear definitions, and the hypothesis should contain:

• The relevant variables
• The specific group being studied
• The predicted outcome of the experiment or analysis

5. Phrase your hypothesis in three ways

To identify the variables, you can write a simple prediction in  if…then form. The first part of the sentence states the independent variable and the second part states the dependent variable.

In academic research, hypotheses are more commonly phrased in terms of correlations or effects, where you directly state the predicted relationship between variables.

If you are comparing two groups, the hypothesis can state what difference you expect to find between them.

6. Write a null hypothesis

If your research involves statistical hypothesis testing , you will also have to write a null hypothesis . The null hypothesis is the default position that there is no association between the variables. The null hypothesis is written as H 0 , while the alternative hypothesis is H 1 or H a .

• H 0 : The number of lectures attended by first-year students has no effect on their final exam scores.
• H 1 : The number of lectures attended by first-year students has a positive effect on their final exam scores.

If you want to know more about the research process , methodology , research bias , or statistics , make sure to check out some of our other articles with explanations and examples.

• Sampling methods
• Simple random sampling
• Stratified sampling
• Cluster sampling
• Likert scales
• Reproducibility

 Statistics

• Null hypothesis
• Statistical power
• Probability distribution
• Effect size
• Poisson distribution

Research bias

• Optimism bias
• Cognitive bias
• Implicit bias
• Hawthorne effect
• Anchoring bias
• Explicit bias

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

McCombes, S. (2023, November 20). How to Write a Strong Hypothesis | Steps & Examples. Scribbr. Retrieved March 12, 2024, from https://www.scribbr.com/methodology/hypothesis/

Is this article helpful?

Shona McCombes

Other students also liked, construct validity | definition, types, & examples, what is a conceptual framework | tips & examples, operationalization | a guide with examples, pros & cons, what is your plagiarism score.

Statistics Made Easy

Introduction to Hypothesis Testing

A statistical hypothesis is an assumption about a population parameter .

For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

The Two Types of Statistical Hypotheses

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

There are two types of statistical hypotheses:

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H 1 or H a , is the hypothesis that the sample data is influenced by some non-random cause.

Hypothesis Tests

A hypothesis test consists of five steps:

1. State the hypotheses. 

State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

2. Determine a significance level to use for the hypothesis.

Decide on a significance level. Common choices are .01, .05, and .1. 

3. Find the test statistic.

Find the test statistic and the corresponding p-value. Often we are analyzing a population mean or proportion and the general formula to find the test statistic is: (sample statistic – population parameter) / (standard deviation of statistic)

4. Reject or fail to reject the null hypothesis.

Using the test statistic or the p-value, determine if you can reject or fail to reject the null hypothesis based on the significance level.

The p-value  tells us the strength of evidence in support of a null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis.

5. Interpret the results. 

Interpret the results of the hypothesis test in the context of the question being asked. 

The Two Types of Decision Errors

There are two types of decision errors that one can make when doing a hypothesis test:

Type I error: You reject the null hypothesis when it is actually true. The probability of committing a Type I error is equal to the significance level, often called  alpha , and denoted as α.

Type II error: You fail to reject the null hypothesis when it is actually false. The probability of committing a Type II error is called the Power of the test or  Beta , denoted as β.

One-Tailed and Two-Tailed Tests

A statistical hypothesis can be one-tailed or two-tailed.

A one-tailed hypothesis involves making a “greater than” or “less than ” statement.

For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches. The null hypothesis would be H0: µ ≥ 70 inches and the alternative hypothesis would be Ha: µ < 70 inches.

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement.

For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null hypothesis would be H0: µ = 70 inches and the alternative hypothesis would be Ha: µ ≠ 70 inches.

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Related:   What is a Directional Hypothesis?

Types of Hypothesis Tests

There are many different types of hypothesis tests you can perform depending on the type of data you’re working with and the goal of your analysis.

The following tutorials provide an explanation of the most common types of hypothesis tests:

Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test Introduction to the One Proportion Z-Test Introduction to the Two Proportion Z-Test

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

• Quality Improvement
• Talk To Minitab

Understanding Hypothesis Tests: Why We Need to Use Hypothesis Tests in Statistics

Topics: Hypothesis Testing , Data Analysis , Statistics

Hypothesis testing is an essential procedure in statistics. A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. When we say that a finding is statistically significant, it’s thanks to a hypothesis test. How do these tests really work and what does statistical significance actually mean?

In this series of three posts, I’ll help you intuitively understand how hypothesis tests work by focusing on concepts and graphs rather than equations and numbers. After all, a key reason to use statistical software like Minitab is so you don’t get bogged down in the calculations and can instead focus on understanding your results.

To kick things off in this post, I highlight the rationale for using hypothesis tests with an example.

The Scenario

An economist wants to determine whether the monthly energy cost for families has changed from the previous year, when the mean cost per month was $260. The economist randomly samples 25 families and records their energy costs for the current year. (The data for this example is FamilyEnergyCost and it is just one of the many data set examples that can be found in Minitab’s Data Set Library.)

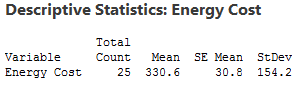
I’ll use these descriptive statistics to create a probability distribution plot that shows you the importance of hypothesis tests. Read on!

The Need for Hypothesis Tests

Why do we even need hypothesis tests? After all, we took a random sample and our sample mean of 330.6 is different from 260. That is different, right? Unfortunately, the picture is muddied because we’re looking at a sample rather than the entire population.

Sampling error is the difference between a sample and the entire population. Thanks to sampling error, it’s entirely possible that while our sample mean is 330.6, the population mean could still be 260. Or, to put it another way, if we repeated the experiment, it’s possible that the second sample mean could be close to 260. A hypothesis test helps assess the likelihood of this possibility!

Use the Sampling Distribution to See If Our Sample Mean is Unlikely

For any given random sample, the mean of the sample almost certainly doesn’t equal the true mean of the population due to sampling error. For our example, it’s unlikely that the mean cost for the entire population is exactly 330.6. In fact, if we took multiple random samples of the same size from the same population, we could plot a distribution of the sample means.

A sampling distribution is the distribution of a statistic, such as the mean, that is obtained by repeatedly drawing a large number of samples from a specific population. This distribution allows you to determine the probability of obtaining the sample statistic.

Fortunately, I can create a plot of sample means without collecting many different random samples! Instead, I’ll create a probability distribution plot using the t-distribution , the sample size, and the variability in our sample to graph the sampling distribution.

Our goal is to determine whether our sample mean is significantly different from the null hypothesis mean. Therefore, we’ll use the graph to see whether our sample mean of 330.6 is unlikely assuming that the population mean is 260. The graph below shows the expected distribution of sample means.

You can see that the most probable sample mean is 260, which makes sense because we’re assuming that the null hypothesis is true. However, there is a reasonable probability of obtaining a sample mean that ranges from 167 to 352, and even beyond! The takeaway from this graph is that while our sample mean of 330.6 is not the most probable, it’s also not outside the realm of possibility.

The Role of Hypothesis Tests

We’ve placed our sample mean in the context of all possible sample means while assuming that the null hypothesis is true. Are these results statistically significant?

As you can see, there is no magic place on the distribution curve to make this determination. Instead, we have a continual decrease in the probability of obtaining sample means that are further from the null hypothesis value. Where do we draw the line?

This is where hypothesis tests are useful. A hypothesis test allows us quantify the probability that our sample mean is unusual.

For this series of posts, I’ll continue to use this graphical framework and add in the significance level, P value, and confidence interval to show how hypothesis tests work and what statistical significance really means.

• Part Two: Significance Levels (alpha) and P values
• Part Three: Confidence Intervals and Confidence Levels

If you'd like to see how I made these graphs, please read: How to Create a Graphical Version of the 1-sample t-Test .

You Might Also Like

• Trust Center

© 2023 Minitab, LLC. All Rights Reserved.

• Terms of Use
• Privacy Policy
• Cookies Settings

• Hypothesis Testing: Definition, Uses, Limitations + Examples

Hypothesis testing is as old as the scientific method and is at the heart of the research process. 

Research exists to validate or disprove assumptions about various phenomena. The process of validation involves testing and it is in this context that we will explore hypothesis testing. 

What is a Hypothesis? 

A hypothesis is a calculated prediction or assumption about a population parameter based on limited evidence. The whole idea behind hypothesis formulation is testing—this means the researcher subjects his or her calculated assumption to a series of evaluations to know whether they are true or false. 

Typically, every research starts with a hypothesis—the investigator makes a claim and experiments to prove that this claim is true or false . For instance, if you predict that students who drink milk before class perform better than those who don’t, then this becomes a hypothesis that can be confirmed or refuted using an experiment.  

Read: What is Empirical Research Study? [Examples & Method]

What are the Types of Hypotheses? 

1. simple hypothesis.

Also known as a basic hypothesis, a simple hypothesis suggests that an independent variable is responsible for a corresponding dependent variable. In other words, an occurrence of the independent variable inevitably leads to an occurrence of the dependent variable. 

Typically, simple hypotheses are considered as generally true, and they establish a causal relationship between two variables. 

Examples of Simple Hypothesis  

• Drinking soda and other sugary drinks can cause obesity. 
• Smoking cigarettes daily leads to lung cancer.

2. Complex Hypothesis

A complex hypothesis is also known as a modal. It accounts for the causal relationship between two independent variables and the resulting dependent variables. This means that the combination of the independent variables leads to the occurrence of the dependent variables . 

Examples of Complex Hypotheses  

• Adults who do not smoke and drink are less likely to develop liver-related conditions.
• Global warming causes icebergs to melt which in turn causes major changes in weather patterns.

3. Null Hypothesis

As the name suggests, a null hypothesis is formed when a researcher suspects that there’s no relationship between the variables in an observation. In this case, the purpose of the research is to approve or disapprove this assumption. 

Examples of Null Hypothesis

• This is no significant change in a student’s performance if they drink coffee or tea before classes. 
• There’s no significant change in the growth of a plant if one uses distilled water only or vitamin-rich water. 

Read: Research Report: Definition, Types + [Writing Guide]

4. Alternative Hypothesis 

To disapprove a null hypothesis, the researcher has to come up with an opposite assumption—this assumption is known as the alternative hypothesis. This means if the null hypothesis says that A is false, the alternative hypothesis assumes that A is true. 

An alternative hypothesis can be directional or non-directional depending on the direction of the difference. A directional alternative hypothesis specifies the direction of the tested relationship, stating that one variable is predicted to be larger or smaller than the null value while a non-directional hypothesis only validates the existence of a difference without stating its direction. 

Examples of Alternative Hypotheses  

• Starting your day with a cup of tea instead of a cup of coffee can make you more alert in the morning. 
• The growth of a plant improves significantly when it receives distilled water instead of vitamin-rich water. 

5. Logical Hypothesis

Logical hypotheses are some of the most common types of calculated assumptions in systematic investigations. It is an attempt to use your reasoning to connect different pieces in research and build a theory using little evidence. In this case, the researcher uses any data available to him, to form a plausible assumption that can be tested. 

Examples of Logical Hypothesis

• Waking up early helps you to have a more productive day. 
• Beings from Mars would not be able to breathe the air in the atmosphere of the Earth. 

6. Empirical Hypothesis  

After forming a logical hypothesis, the next step is to create an empirical or working hypothesis. At this stage, your logical hypothesis undergoes systematic testing to prove or disprove the assumption. An empirical hypothesis is subject to several variables that can trigger changes and lead to specific outcomes. 

Examples of Empirical Testing 

• People who eat more fish run faster than people who eat meat.
• Women taking vitamin E grow hair faster than those taking vitamin K.

7. Statistical Hypothesis

When forming a statistical hypothesis, the researcher examines the portion of a population of interest and makes a calculated assumption based on the data from this sample. A statistical hypothesis is most common with systematic investigations involving a large target audience. Here, it’s impossible to collect responses from every member of the population so you have to depend on data from your sample and extrapolate the results to the wider population. 

Examples of Statistical Hypothesis  

• 45% of students in Louisiana have middle-income parents. 
• 80% of the UK’s population gets a divorce because of irreconcilable differences.

What is Hypothesis Testing? 

Hypothesis testing is an assessment method that allows researchers to determine the plausibility of a hypothesis. It involves testing an assumption about a specific population parameter to know whether it’s true or false. These population parameters include variance, standard deviation, and median. 

Typically, hypothesis testing starts with developing a null hypothesis and then performing several tests that support or reject the null hypothesis. The researcher uses test statistics to compare the association or relationship between two or more variables. 

Explore: Research Bias: Definition, Types + Examples

Researchers also use hypothesis testing to calculate the coefficient of variation and determine if the regression relationship and the correlation coefficient are statistically significant.

How Hypothesis Testing Works

The basis of hypothesis testing is to examine and analyze the null hypothesis and alternative hypothesis to know which one is the most plausible assumption. Since both assumptions are mutually exclusive, only one can be true. In other words, the occurrence of a null hypothesis destroys the chances of the alternative coming to life, and vice-versa. 

Interesting: 21 Chrome Extensions for Academic Researchers in 2021

What Are The Stages of Hypothesis Testing?  

To successfully confirm or refute an assumption, the researcher goes through five (5) stages of hypothesis testing; 

• Determine the null hypothesis
• Specify the alternative hypothesis
• Set the significance level
• Calculate the test statistics and corresponding P-value
• Draw your conclusion
• Determine the Null Hypothesis

Like we mentioned earlier, hypothesis testing starts with creating a null hypothesis which stands as an assumption that a certain statement is false or implausible. For example, the null hypothesis (H0) could suggest that different subgroups in the research population react to a variable in the same way. 

• Specify the Alternative Hypothesis

Once you know the variables for the null hypothesis, the next step is to determine the alternative hypothesis. The alternative hypothesis counters the null assumption by suggesting the statement or assertion is true. Depending on the purpose of your research, the alternative hypothesis can be one-sided or two-sided. 

Using the example we established earlier, the alternative hypothesis may argue that the different sub-groups react differently to the same variable based on several internal and external factors. 

• Set the Significance Level

Many researchers create a 5% allowance for accepting the value of an alternative hypothesis, even if the value is untrue. This means that there is a 0.05 chance that one would go with the value of the alternative hypothesis, despite the truth of the null hypothesis. 

Something to note here is that the smaller the significance level, the greater the burden of proof needed to reject the null hypothesis and support the alternative hypothesis.

Explore: What is Data Interpretation? + [Types, Method & Tools]

• Calculate the Test Statistics and Corresponding P-Value 

Test statistics in hypothesis testing allow you to compare different groups between variables while the p-value accounts for the probability of obtaining sample statistics if your null hypothesis is true. In this case, your test statistics can be the mean, median and similar parameters. 

If your p-value is 0.65, for example, then it means that the variable in your hypothesis will happen 65 in100 times by pure chance. Use this formula to determine the p-value for your data: 

• Draw Your Conclusions

After conducting a series of tests, you should be able to agree or refute the hypothesis based on feedback and insights from your sample data.  

Applications of Hypothesis Testing in Research

Hypothesis testing isn’t only confined to numbers and calculations; it also has several real-life applications in business, manufacturing, advertising, and medicine. 

In a factory or other manufacturing plants, hypothesis testing is an important part of quality and production control before the final products are approved and sent out to the consumer. 

During ideation and strategy development, C-level executives use hypothesis testing to evaluate their theories and assumptions before any form of implementation. For example, they could leverage hypothesis testing to determine whether or not some new advertising campaign, marketing technique, etc. causes increased sales. 

In addition, hypothesis testing is used during clinical trials to prove the efficacy of a drug or new medical method before its approval for widespread human usage. 

What is an Example of Hypothesis Testing?

An employer claims that her workers are of above-average intelligence. She takes a random sample of 20 of them and gets the following results: 

Mean IQ Scores: 110

Standard Deviation: 15 

Mean Population IQ: 100

Step 1: Using the value of the mean population IQ, we establish the null hypothesis as 100.

Step 2: State that the alternative hypothesis is greater than 100.

Step 3: State the alpha level as 0.05 or 5% 

Step 4: Find the rejection region area (given by your alpha level above) from the z-table. An area of .05 is equal to a z-score of 1.645.

Step 5: Calculate the test statistics using this formula

Z = (110–100) ÷ (15÷√20) 

10 ÷ 3.35 = 2.99 

If the value of the test statistics is higher than the value of the rejection region, then you should reject the null hypothesis. If it is less, then you cannot reject the null. 

In this case, 2.99 > 1.645 so we reject the null. 

Importance/Benefits of Hypothesis Testing 

The most significant benefit of hypothesis testing is it allows you to evaluate the strength of your claim or assumption before implementing it in your data set. Also, hypothesis testing is the only valid method to prove that something “is or is not”. Other benefits include: 

• Hypothesis testing provides a reliable framework for making any data decisions for your population of interest. 
• It helps the researcher to successfully extrapolate data from the sample to the larger population. 
• Hypothesis testing allows the researcher to determine whether the data from the sample is statistically significant. 
• Hypothesis testing is one of the most important processes for measuring the validity and reliability of outcomes in any systematic investigation. 
• It helps to provide links to the underlying theory and specific research questions.

Criticism and Limitations of Hypothesis Testing

Several limitations of hypothesis testing can affect the quality of data you get from this process. Some of these limitations include: 

• The interpretation of a p-value for observation depends on the stopping rule and definition of multiple comparisons. This makes it difficult to calculate since the stopping rule is subject to numerous interpretations, plus “multiple comparisons” are unavoidably ambiguous. 
• Conceptual issues often arise in hypothesis testing, especially if the researcher merges Fisher and Neyman-Pearson’s methods which are conceptually distinct. 
• In an attempt to focus on the statistical significance of the data, the researcher might ignore the estimation and confirmation by repeated experiments.
• Hypothesis testing can trigger publication bias, especially when it requires statistical significance as a criterion for publication.
• When used to detect whether a difference exists between groups, hypothesis testing can trigger absurd assumptions that affect the reliability of your observation.

Connect to Formplus, Get Started Now - It's Free!

• alternative hypothesis
• alternative vs null hypothesis
• complex hypothesis
• empirical hypothesis
• hypothesis testing
• logical hypothesis
• simple hypothesis
• statistical hypothesis
• busayo.longe

You may also like:

What is Pure or Basic Research? + [Examples & Method]

Simple guide on pure or basic research, its methods, characteristics, advantages, and examples in science, medicine, education and psychology

Alternative vs Null Hypothesis: Pros, Cons, Uses & Examples

We are going to discuss alternative hypotheses and null hypotheses in this post and how they work in research.

Internal Validity in Research: Definition, Threats, Examples

In this article, we will discuss the concept of internal validity, some clear examples, its importance, and how to test it.

Type I vs Type II Errors: Causes, Examples & Prevention

This article will discuss the two different types of errors in hypothesis testing and how you can prevent them from occurring in your research

Formplus - For Seamless Data Collection

Collect data the right way with a versatile data collection tool. try formplus and transform your work productivity today..

• Business Essentials
• Leadership & Management
• Credential of Leadership, Impact, and Management in Business (CLIMB)
• Entrepreneurship & Innovation
• *New* Digital Transformation
• Finance & Accounting
• Business in Society
• For Organizations
• Support Portal
• Media Coverage
• Founding Donors
• Leadership Team

• Harvard Business School →
• HBS Online →
• Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

• Career Development
• Communication
• Decision-Making
• Earning Your MBA
• Negotiation
• News & Events
• Productivity
• Staff Spotlight
• Student Profiles
• Work-Life Balance
• Alternative Investments
• Business Analytics
• Business Strategy
• Business and Climate Change
• Design Thinking and Innovation
• Digital Marketing Strategy
• Disruptive Strategy
• Economics for Managers
• Entrepreneurship Essentials
• Financial Accounting
• Global Business
• Launching Tech Ventures
• Leadership Principles
• Leadership, Ethics, and Corporate Accountability
• Leading with Finance
• Management Essentials
• Negotiation Mastery
• Organizational Leadership
• Power and Influence for Positive Impact
• Strategy Execution
• Sustainable Business Strategy
• Sustainable Investing
• Winning with Digital Platforms

A Beginner’s Guide to Hypothesis Testing in Business

• 30 Mar 2021

Becoming a more data-driven decision-maker can bring several benefits to your organization, enabling you to identify new opportunities to pursue and threats to abate. Rather than allowing subjective thinking to guide your business strategy, backing your decisions with data can empower your company to become more innovative and, ultimately, profitable.

If you’re new to data-driven decision-making, you might be wondering how data translates into business strategy. The answer lies in generating a hypothesis and verifying or rejecting it based on what various forms of data tell you.

Below is a look at hypothesis testing and the role it plays in helping businesses become more data-driven.

Access your free e-book today.

What Is Hypothesis Testing?

To understand what hypothesis testing is, it’s important first to understand what a hypothesis is.

A hypothesis or hypothesis statement seeks to explain why something has happened, or what might happen, under certain conditions. It can also be used to understand how different variables relate to each other. Hypotheses are often written as if-then statements; for example, “If this happens, then this will happen.”

Hypothesis testing , then, is a statistical means of testing an assumption stated in a hypothesis. While the specific methodology leveraged depends on the nature of the hypothesis and data available, hypothesis testing typically uses sample data to extrapolate insights about a larger population.

Hypothesis Testing in Business

When it comes to data-driven decision-making, there’s a certain amount of risk that can mislead a professional. This could be due to flawed thinking or observations, incomplete or inaccurate data , or the presence of unknown variables. The danger in this is that, if major strategic decisions are made based on flawed insights, it can lead to wasted resources, missed opportunities, and catastrophic outcomes.

The real value of hypothesis testing in business is that it allows professionals to test their theories and assumptions before putting them into action. This essentially allows an organization to verify its analysis is correct before committing resources to implement a broader strategy.

As one example, consider a company that wishes to launch a new marketing campaign to revitalize sales during a slow period. Doing so could be an incredibly expensive endeavor, depending on the campaign’s size and complexity. The company, therefore, may wish to test the campaign on a smaller scale to understand how it will perform.

In this example, the hypothesis that’s being tested would fall along the lines of: “If the company launches a new marketing campaign, then it will translate into an increase in sales.” It may even be possible to quantify how much of a lift in sales the company expects to see from the effort. Pending the results of the pilot campaign, the business would then know whether it makes sense to roll it out more broadly.

Related: 9 Fundamental Data Science Skills for Business Professionals

Key Considerations for Hypothesis Testing

1. alternative hypothesis and null hypothesis.

In hypothesis testing, the hypothesis that’s being tested is known as the alternative hypothesis . Often, it’s expressed as a correlation or statistical relationship between variables. The null hypothesis , on the other hand, is a statement that’s meant to show there’s no statistical relationship between the variables being tested. It’s typically the exact opposite of whatever is stated in the alternative hypothesis.

For example, consider a company’s leadership team that historically and reliably sees $12 million in monthly revenue. They want to understand if reducing the price of their services will attract more customers and, in turn, increase revenue.

In this case, the alternative hypothesis may take the form of a statement such as: “If we reduce the price of our flagship service by five percent, then we’ll see an increase in sales and realize revenues greater than $12 million in the next month.”

The null hypothesis, on the other hand, would indicate that revenues wouldn’t increase from the base of $12 million, or might even decrease.

Check out the video below about the difference between an alternative and a null hypothesis, and subscribe to our YouTube channel for more explainer content.

2. Significance Level and P-Value

Statistically speaking, if you were to run the same scenario 100 times, you’d likely receive somewhat different results each time. If you were to plot these results in a distribution plot, you’d see the most likely outcome is at the tallest point in the graph, with less likely outcomes falling to the right and left of that point.

With this in mind, imagine you’ve completed your hypothesis test and have your results, which indicate there may be a correlation between the variables you were testing. To understand your results' significance, you’ll need to identify a p-value for the test, which helps note how confident you are in the test results.

In statistics, the p-value depicts the probability that, assuming the null hypothesis is correct, you might still observe results that are at least as extreme as the results of your hypothesis test. The smaller the p-value, the more likely the alternative hypothesis is correct, and the greater the significance of your results.

3. One-Sided vs. Two-Sided Testing

When it’s time to test your hypothesis, it’s important to leverage the correct testing method. The two most common hypothesis testing methods are one-sided and two-sided tests , or one-tailed and two-tailed tests, respectively.

Typically, you’d leverage a one-sided test when you have a strong conviction about the direction of change you expect to see due to your hypothesis test. You’d leverage a two-sided test when you’re less confident in the direction of change.

4. Sampling

To perform hypothesis testing in the first place, you need to collect a sample of data to be analyzed. Depending on the question you’re seeking to answer or investigate, you might collect samples through surveys, observational studies, or experiments.

A survey involves asking a series of questions to a random population sample and recording self-reported responses.

Observational studies involve a researcher observing a sample population and collecting data as it occurs naturally, without intervention.

Finally, an experiment involves dividing a sample into multiple groups, one of which acts as the control group. For each non-control group, the variable being studied is manipulated to determine how the data collected differs from that of the control group.

Learn How to Perform Hypothesis Testing

Hypothesis testing is a complex process involving different moving pieces that can allow an organization to effectively leverage its data and inform strategic decisions.

If you’re interested in better understanding hypothesis testing and the role it can play within your organization, one option is to complete a course that focuses on the process. Doing so can lay the statistical and analytical foundation you need to succeed.

Do you want to learn more about hypothesis testing? Explore Business Analytics —one of our online business essentials courses —and download our Beginner’s Guide to Data & Analytics .

About the Author

Teach yourself statistics

How to Test Statistical Hypotheses

This lesson describes a general procedure that can be used to test statistical hypotheses.

How to Conduct Hypothesis Tests

All hypothesis tests are conducted the same way. The researcher states a hypothesis to be tested, formulates an analysis plan, analyzes sample data according to the plan, and accepts or rejects the null hypothesis, based on results of the analysis.

• State the hypotheses. Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.
• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Typically, the test method involves a test statistic and a sampling distribution . Computed from sample data, the test statistic might be a mean score, proportion, difference between means, difference between proportions, z-score, t statistic, chi-square, etc. Given a test statistic and its sampling distribution, a researcher can assess probabilities associated with the test statistic. If the test statistic probability is less than the significance level, the null hypothesis is rejected.

Test statistic = (Statistic - Parameter) / (Standard deviation of statistic)

Test statistic = (Statistic - Parameter) / (Standard error of statistic)

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic, assuming the null hypothesis is true.
• Interpret the results. If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Applications of the General Hypothesis Testing Procedure

The next few lessons show how to apply the general hypothesis testing procedure to different kinds of statistical problems.

• Proportions
• Difference between proportions
• Regression slope
• Difference between means
• Difference between matched pairs
• Goodness of fit
• Homogeneity
• Independence

At this point, don't worry if the general procedure for testing hypotheses seems a little bit unclear. The procedure will be clearer as you see it applied in the next few lessons.

Test Your Understanding

In hypothesis testing, which of the following statements is always true?

I. The P-value is greater than the significance level. II. The P-value is computed from the significance level. III. The P-value is the parameter in the null hypothesis. IV. The P-value is a test statistic. V. The P-value is a probability.

(A) I only (B) II only (C) III only (D) IV only (E) V only

The correct answer is (E). The P-value is the probability of observing a sample statistic as extreme as the test statistic. It can be greater than the significance level, but it can also be smaller than the significance level. It is not computed from the significance level, it is not the parameter in the null hypothesis, and it is not a test statistic.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Advanced Search
• Journal List
• R Soc Open Sci
• v.10(8); 2023 Aug
• PMC10465209

On the scope of scientific hypotheses

William hedley thompson.

1 Department of Applied Information Technology, University of Gothenburg, Gothenburg, Sweden

2 Institute of Neuroscience and Physiology, Sahlgrenska Academy, University of Gothenburg, Gothenburg, Sweden

3 Department of Pedagogical, Curricular and Professional Studies, Faculty of Education, University of Gothenburg, Gothenburg, Sweden

4 Department of Clinical Neuroscience, Karolinska Institutet, Stockholm, Sweden

Associated Data

This article has no additional data.

Hypotheses are frequently the starting point when undertaking the empirical portion of the scientific process. They state something that the scientific process will attempt to evaluate, corroborate, verify or falsify. Their purpose is to guide the types of data we collect, analyses we conduct, and inferences we would like to make. Over the last decade, metascience has advocated for hypotheses being in preregistrations or registered reports, but how to formulate these hypotheses has received less attention. Here, we argue that hypotheses can vary in specificity along at least three independent dimensions: the relationship, the variables, and the pipeline. Together, these dimensions form the scope of the hypothesis. We demonstrate how narrowing the scope of a hypothesis in any of these three ways reduces the hypothesis space and that this reduction is a type of novelty. Finally, we discuss how this formulation of hypotheses can guide researchers to formulate the appropriate scope for their hypotheses and should aim for neither too broad nor too narrow a scope. This framework can guide hypothesis-makers when formulating their hypotheses by helping clarify what is being tested, chaining results to previous known findings, and demarcating what is explicitly tested in the hypothesis.

1.  Introduction

Hypotheses are an important part of the scientific process. However, surprisingly little attention is given to hypothesis-making compared to other skills in the scientist's skillset within current discussions aimed at improving scientific practice. Perhaps this lack of emphasis is because the formulation of the hypothesis is often considered less relevant, as it is ultimately the scientific process that will eventually decide the veracity of the hypothesis. However, there are more hypotheses than scientific studies as selection occurs at various stages: from funder selection and researcher's interests. So which hypotheses are worthwhile to pursue? Which hypotheses are the most effective or pragmatic for extending or enhancing our collective knowledge? We consider the answer to these questions by discussing how broad or narrow a hypothesis can or should be (i.e. its scope).

We begin by considering that the two statements below are both hypotheses and vary in scope:

• H 1 : For every 1 mg decrease of x , y will increase by, on average, 2.5 points.
• H 2 : Changes in x 1 or x 2 correlate with y levels in some way.

Clearly, the specificity of the two hypotheses is very different. H 1 states a precise relationship between two variables ( x and y ), while H 2 specifies a vaguer relationship and does not specify which variables will show the relationship. However, they are both still hypotheses about how x and y relate to each other. This claim of various degrees of the broadness of hypotheses is, in and of itself, not novel. In Epistemetrics, Rescher [ 1 ], while drawing upon the physicist Duhem's work, develops what he calls Duhem's Law. This law considers a trade-off between certainty or precision in statements about physics when evaluating them. Duhem's Law states that narrower hypotheses, such as H 1 above, are more precise but less likely to be evaluated as true than broader ones, such as H 2 above. Similarly, Popper, when discussing theories, describes the reverse relationship between content and probability of a theory being true, i.e. with increased content, there is a decrease in probability and vice versa [ 2 ]. Here we will argue that it is important that both H 1 and H 2 are still valid scientific hypotheses, and their appropriateness depends on certain scientific questions.

The question of hypothesis scope is relevant since there are multiple recent prescriptions to improve science, ranging from topics about preregistrations [ 3 ], registered reports [ 4 ], open science [ 5 ], standardization [ 6 ], generalizability [ 7 ], multiverse analyses [ 8 ], dataset reuse [ 9 ] and general questionable research practices [ 10 ]. Within each of these issues, there are arguments to demarcate between confirmatory and exploratory research or normative prescriptions about how science should be done (e.g. science is ‘bad’ or ‘worse’ if code/data are not open). Despite all these discussions and improvements, much can still be done to improve hypothesis-making. A recent evaluation of preregistered studies in psychology found that over half excluded the preregistered hypotheses [ 11 ]. Further, evaluations of hypotheses in ecology showed that most hypotheses are not explicitly stated [ 12 , 13 ]. Other research has shown that obfuscated hypotheses are more prevalent in retracted research [ 14 ]. There have been recommendations for simpler hypotheses in psychology to avoid misinterpretations and misspecifications [ 15 ]. Finally, several evaluations of preregistration practices have found that a significant proportion of articles do not abide by their stated hypothesis or add additional hypotheses [ 11 , 16 – 18 ]. In sum, while multiple efforts exist to improve scientific practice, our hypothesis-making could improve.

One of our intentions is to provide hypothesis-makers with tools to assist them when making hypotheses. We consider this useful and timely as, with preregistrations becoming more frequent, the hypothesis-making process is now open and explicit . However, preregistrations are difficult to write [ 19 ], and preregistered articles can change or omit hypotheses [ 11 ] or they are vague and certain degrees of freedom hard to control for [ 16 – 18 ]. One suggestion has been to do less confirmatory research [ 7 , 20 ]. While we agree that all research does not need to be confirmatory, we also believe that not all preregistrations of confirmatory work must test narrow hypotheses. We think there is a possible point of confusion that the specificity in preregistrations, where researcher degrees of freedom should be stated, necessitates the requirement that the hypothesis be narrow. Our belief that this confusion is occurring is supported by the study Akker et al . [ 11 ] where they found that 18% of published psychology studies changed their preregistered hypothesis (e.g. its direction), and 60% of studies selectively reported hypotheses in some way. It is along these lines that we feel the framework below can be useful to help formulate appropriate hypotheses to mitigate these identified issues.

We consider this article to be a discussion of the researcher's different choices when formulating hypotheses and to help link hypotheses over time. Here we aim to deconstruct what aspects there are in the hypothesis about their specificity. Throughout this article, we intend to be neutral to many different philosophies of science relating to the scientific method (i.e. how one determines the veracity of a hypothesis). Our idea of neutrality here is that whether a researcher adheres to falsification, verification, pragmatism, or some other philosophy of science, then this framework can be used when formulating hypotheses. 1

The framework this article advocates for is that there are (at least) three dimensions that hypotheses vary along regarding their narrowness and broadness: the selection of relationships, variables, and pipelines. We believe this discussion is fruitful for the current debate regarding normative practices as some positions make, sometimes implicit, commitments about which set of hypotheses the scientific community ought to consider good or permissible. We proceed by outlining a working definition of ‘scientific hypothesis' and then discuss how it relates to theory. Then, we justify how hypotheses can vary along the three dimensions. Using this framework, we then discuss the scopes in relation to appropriate hypothesis-making and an argument about what constitutes a scientifically novel hypothesis. We end the article with practical advice for researchers who wish to use this framework.

2.  The scientific hypothesis

In this section, we will describe a functional and descriptive role regarding how scientists use hypotheses. Jeong & Kwon [ 21 ] investigated and summarized the different uses the concept of ‘hypothesis’ had in philosophical and scientific texts. They identified five meanings: assumption, tentative explanation, tentative cause, tentative law, and prediction. Jeong & Kwon [ 21 ] further found that researchers in science and philosophy used all the different definitions of hypotheses, although there was some variance in frequency between fields. Here we see, descriptively , that the way researchers use the word ‘hypothesis’ is diverse and has a wide range in specificity and function. However, whichever meaning a hypothesis has, it aims to be true, adequate, accurate or useful in some way.

Not all hypotheses are ‘scientific hypotheses'. For example, consider the detective trying to solve a crime and hypothesizing about the perpetrator. Such a hypothesis still aims to be true and is a tentative explanation but differs from the scientific hypothesis. The difference is that the researcher, unlike the detective, evaluates the hypothesis with the scientific method and submits the work for evaluation by the scientific community. Thus a scientific hypothesis entails a commitment to evaluate the statement with the scientific process . 2 Additionally, other types of hypotheses can exist. As discussed in more detail below, scientific theories generate not only scientific hypotheses but also contain auxiliary hypotheses. The latter refers to additional assumptions considered to be true and not explicitly evaluated. 3

Next, the scientific hypothesis is generally made antecedent to the evaluation. This does not necessitate that the event (e.g. in archaeology) or the data collection (e.g. with open data reuse) must be collected before the hypothesis is made, but that the evaluation of the hypothesis cannot happen before its formulation. This claim state does deny the utility of exploratory hypothesis testing of post hoc hypotheses (see [ 25 ]). However, previous results and exploration can generate new hypotheses (e.g. via abduction [ 22 , 26 – 28 ], which is the process of creating hypotheses from evidence), which is an important part of science [ 29 – 32 ], but crucially, while these hypotheses are important and can be the conclusion of exploratory work, they have yet to be evaluated (by whichever method of choice). Hence, they still conform to the antecedency requirement. A further way to justify the antecedency is seen in the practice of formulating a post hoc hypothesis, and considering it to have been evaluated is seen as a questionable research practice (known as ‘hypotheses after results are known’ or HARKing [ 33 ]). 4

While there is a varying range of specificity, is the hypothesis a critical part of all scientific work, or is it reserved for some subset of investigations? There are different opinions regarding this. Glass and Hall, for example, argue that the term only refers to falsifiable research, and model-based research uses verification [ 36 ]. However, this opinion does not appear to be the consensus. Osimo and Rumiati argue that any model based on or using data is never wholly free from hypotheses, as hypotheses can, even implicitly, infiltrate the data collection [ 37 ]. For our definition, we will consider hypotheses that can be involved in different forms of scientific evaluation (i.e. not just falsification), but we do not exclude the possibility of hypothesis-free scientific work.

Finally, there is a debate about whether theories or hypotheses should be linguistic or formal [ 38 – 40 ]. Neither side in this debate argues that verbal or formal hypotheses are not possible, but instead, they discuss normative practices. Thus, for our definition, both linguistic and formal hypotheses are considered viable.

Considering the above discussion, let us summarize the scientific process and the scientific hypothesis: a hypothesis guides what type of data are sampled and what analysis will be done. With the new observations, evidence is analysed or quantified in some way (often using inferential statistics) to judge the hypothesis's truth value, utility, credibility, or likelihood. The following working definition captures the above:

• Scientific hypothesis : an implicit or explicit statement that can be verbal or formal. The hypothesis makes a statement about some natural phenomena (via an assumption, explanation, cause, law or prediction). The scientific hypothesis is made antecedent to performing a scientific process where there is a commitment to evaluate it.

For simplicity, we will only use the term ‘hypothesis’ for ‘scientific hypothesis' to refer to the above definition for the rest of the article except when it is necessary to distinguish between other types of hypotheses. Finally, this definition could further be restrained in multiple ways (e.g. only explicit hypotheses are allowed, or assumptions are never hypotheses). However, if the definition is more (or less) restrictive, it has little implication for the argument below.

3.  The hypothesis, theory and auxiliary assumptions

While we have a definition of the scientific hypothesis, we have yet to link it with how it relates to scientific theory, where there is frequently some interconnection (i.e. a hypothesis tests a scientific theory). Generally, for this paper, we believe our argument applies regardless of how scientific theory is defined. Further, some research lacks theory, sometimes called convenience or atheoretical studies [ 41 ]. Here a hypothesis can be made without a wider theory—and our framework fits here too. However, since many consider hypotheses to be defined or deducible from scientific theory, there is an important connection between the two. Therefore, we will briefly clarify how hypotheses relate to common formulations of scientific theory.

A scientific theory is generally a set of axioms or statements about some objects, properties and their relations relating to some phenomena. Hypotheses can often be deduced from the theory. Additionally, a theory has boundary conditions. The boundary conditions specify the domain of the theory stating under what conditions it applies (e.g. all things with a central neural system, humans, women, university teachers) [ 42 ]. Boundary conditions of a theory will consequently limit all hypotheses deduced from the theory. For example, with a boundary condition ‘applies to all humans’, then the subsequent hypotheses deduced from the theory are limited to being about humans. While this limitation of the hypothesis by the theory's boundary condition exists, all the considerations about a hypothesis scope detailed below still apply within the boundary conditions. Finally, it is also possible (depending on the definition of scientific theory) for a hypothesis to test the same theory under different boundary conditions. 5

The final consideration relating scientific theory to scientific hypotheses is auxiliary hypotheses. These hypotheses are theories or assumptions that are considered true simultaneously with the theory. Most philosophies of science from Popper's background knowledge [ 24 ], Kuhn's paradigms during normal science [ 44 ], and Laktos' protective belt [ 45 ] all have their own versions of this auxiliary or background information that is required for the hypothesis to test the theory. For example, Meelh [ 46 ] auxiliary theories/assumptions are needed to go from theoretical terms to empirical terms (e.g. neural activity can be inferred from blood oxygenation in fMRI research or reaction time to an indicator of cognition) and auxiliary theories about instruments (e.g. the experimental apparatus works as intended) and more (see also Other approaches to categorizing hypotheses below). As noted in the previous section, there is a difference between these auxiliary hypotheses, regardless of their definition, and the scientific hypothesis defined above. Recall that our definition of the scientific hypothesis included a commitment to evaluate it. There are no such commitments with auxiliary hypotheses, but rather they are assumed to be correct to test the theory adequately. This distinction proves to be important as auxiliary hypotheses are still part of testing a theory but are separate from the hypothesis to be evaluated (discussed in more detail below).

4.  The scope of hypotheses

In the scientific hypothesis section, we defined the hypothesis and discussed how it relates back to the theory. In this section, we want to defend two claims about hypotheses:

• (A1) Hypotheses can have different scopes . Some hypotheses are narrower in their formulation, and some are broader.
• (A2) The scope of hypotheses can vary along three dimensions relating to relationship selection , variable selection , and pipeline selection .

A1 may seem obvious, but it is important to establish what is meant by narrower and broader scope. When a hypothesis is very narrow, it is specific. For example, it might be specific about the type of relationship between some variables. In figure 1 , we make four different statements regarding the relationship between x and y . The narrowest hypothesis here states ‘there is a positive linear relationship with a magnitude of 0.5 between x and y ’ ( figure 1 a ), and the broadest hypothesis states ‘there is a relationship between x and y ’ ( figure 1 d ). Note that many other hypotheses are possible that are not included in this example (such as there being no relationship).

Examples of narrow and broad hypotheses between x and y . Circles indicate a set of possible relationships with varying slopes that can pivot or bend.

We see that the narrowest of these hypotheses claims a type of relationship (linear), a direction of the relationship (positive) and a magnitude of the relationship (0.5). As the hypothesis becomes broader, the specific magnitude disappears ( figure 1 b ), the relationship has additional options than just being linear ( figure 1 c ), and finally, the direction of the relationship disappears. Crucially, all the examples in figure 1 can meet the above definition of scientific hypotheses. They are all statements that can be evaluated with the same scientific method. There is a difference between these statements, though— they differ in the scope of the hypothesis . Here we have justified A1.

Within this framework, when we discuss whether a hypothesis is narrower or broader in scope, this is a relation between two hypotheses where one is a subset of the other. This means that if H 1 is narrower than H 2 , and if H 1 is true, then H 2 is also true. This can be seen in figure 1 a–d . Suppose figure 1 a , the narrowest of all the hypotheses, is true. In that case, all the other broader statements are also true (i.e. a linear correlation of 0.5 necessarily entails that there is also a positive linear correlation, a linear correlation, and some relationship). While this property may appear trivial, it entails that it is only possible to directly compare the hypothesis scope between two hypotheses (i.e. their broadness or narrowness) where one is the subset of the other. 6

4.1. Sets, disjunctions and conjunctions of elements

The above restraint defines the scope as relations between sets. This property helps formalize the framework of this article. Below, when we discuss the different dimensions that can impact the scope, these become represented as a set. Each set contains elements. Each element is a permissible situation that allows the hypothesis to be accepted. We denote elements as lower case with italics (e.g. e 1 , e 2 , e 3 ) and sets as bold upper case (e.g. S ). Each of the three different dimensions discussed below will be formalized as sets, while the total number of elements specifies their scope.

Let us reconsider the above restraint about comparing hypotheses as narrower or broader. This can be formally shown if:

• e 1 , e 2 , e 3 are elements of S 1 ; and
• e 1 and e 2 are elements of S 2 ,

then S 2 is narrower than S 1 .

Each element represents specific propositions that, if corroborated, would support the hypothesis. Returning to figure 1 a , b , the following statements apply to both:

• ‘There is a positive linear relationship between x and y with a slope of 0.5’.

Whereas the following two apply to figure 1 b but not figure 1 a :

• ‘There is a positive linear relationship between x and y with a slope of 0.4’ ( figure 1 b ).
• ‘There is a positive linear relationship between x and y with a slope of 0.3’ ( figure 1 b ).

Figure 1 b allows for a considerably larger number of permissible situations (which is obvious as it allows for any positive linear relationship). When formulating the hypothesis in figure 1 b , we do not need to specify every single one of these permissible relationships. We can simply specify all possible positive slopes, which entails the set of permissible elements it includes.

That broader hypotheses have more elements in their sets entails some important properties. When we say S contains the elements e 1 , e 2 , and e 3 , the hypothesis is corroborated if e 1 or e 2 or e 3 is the case. This means that the set requires only one of the elements to be corroborated for the hypothesis to be considered correct (i.e. the positive linear relationship needs to be 0.3 or 0.4 or 0.5). Contrastingly, we will later see cases when conjunctions of elements occur (i.e. both e 1 and e 2 are the case). When a conjunction occurs, in this formulation, the conjunction itself becomes an element in the set (i.e. ‘ e 1 and e 2 ’ is a single element). Figure 2 illustrates how ‘ e 1 and e 2 ’ is narrower than ‘ e 1 ’, and ‘ e 1 ’ is narrower than ‘ e 1 or e 2 ’. 7 This property relating to the conjunction being narrower than individual elements is explained in more detail in the pipeline selection section below.

Scope as sets. Left : four different sets (grey, red, blue and purple) showing different elements which they contain. Right : a list of each colour explaining which set is a subset of the other (thereby being ‘narrower’).

4.2. Relationship selection

We move to A2, which is to show the different dimensions that a hypothesis scope can vary along. We have already seen an example of the first dimension of a hypothesis in figure 1 , the relationship selection . Let R denote the set of all possible configurations of relationships that are permissible for the hypothesis to be considered true. For example, in the narrowest formulation above, there was one allowed relationship for the hypothesis to be true. Consequently, the size of R (denoted | R |) is one. As discussed above, in the second narrowest formulation ( figure 1 b ), R has more possible relationships where it can still be considered true:

• r 1 = ‘a positive linear relationship of 0.1’
• r 2 = ‘a positive linear relationship of 0.2’
• r 3 = ‘a positive linear relationship of 0.3’.

Additionally, even broader hypotheses will be compatible with more types of relationships. In figure 1 c , d , nonlinear and negative relationships are also possible relationships included in R . For this broader statement to be affirmed, more elements are possible to be true. Thus if | R | is greater (i.e. contains more possible configurations for the hypothesis to be true), then the hypothesis is broader. Thus, the scope of relating to the relationship selection is specified by | R |. Finally, if |R H1 | > |R H2 | , then H 1 is broader than H 2 regarding the relationship selection.

Figure 1 is an example of the relationship narrowing. That the relationship became linear is only an example and does not necessitate a linear relationship or that this scope refers only to correlations. An alternative example of a relationship scope is a broad hypothesis where there is no knowledge about the distribution of some data. In such situations, one may assume a uniform relationship or a Cauchy distribution centred at zero. Over time the specific distribution can be hypothesized. Thereafter, the various parameters of the distribution can be hypothesized. At each step, the hypothesis of the distribution gets further specified to narrower formulations where a smaller set of possible relationships are included (see [ 47 , 48 ] for a more in-depth discussion about how specific priors relate to more narrow tests). Finally, while figure 1 was used to illustrate the point of increasingly narrow relationship hypotheses, it is more likely to expect the narrowest relationship, within fields such as psychology, to have considerable uncertainty and be formulated with confidence or credible intervals (i.e. we will rarely reach point estimates).

4.3. Variable selection

We have demonstrated that relationship selection can affect the scope of a hypothesis. Additionally, at least two other dimensions can affect the scope of a hypothesis: variable selection and pipeline selection . The variable selection in figure 1 was a single bivariate relationship (e.g. x 's relationship with y ). However, it is not always the case that we know which variables will be involved. For example, in neuroimaging, we can be confident that one or more brain regions will be processing some information following a stimulus. Still, we might not be sure which brain region(s) this will be. Consequently, our hypothesis becomes broader because we have selected more variables. The relationship selection may be identical for each chosen variable, but the variable selection becomes broader. We can consider the following three hypotheses to be increasing in their scope:

• H 1 : x relates to y with relationship R .
• H 2 : x 1 or x 2 relates to y with relationship R .
• H 3 : x 1 or x 2 or x 3 relates to y with relationship R .

For H 1 –H 3 above, we assume that R is the same. Further, we assume that there is no interaction between these variables.

In the above examples, we have multiple x ( x 1 , x 2 , x 3 , … , x n ). Again, we can symbolize the variable selection as a non-empty set XY , containing either a single variable or many variables. Our motivation for designating it XY is that the variable selection can include multiple possibilities for both the independent variable ( x ) and the dependent variable ( y ). Like with relationship selection, we can quantify the broadness between two hypotheses with the size of the set XY . Consequently, | XY | denotes the total scope concerning variable selection. Thus, in the examples above | XY H1 | < | XY H2 | < | XY H3 |. Like with relationship selection, hypotheses that vary in | XY | still meet the definition of a hypothesis. 8

An obvious concern for many is that a broader XY is much easier to evaluate as correct. Generally, when | XY 1 | > | XY 2 |, there is a greater chance of spurious correlations when evaluating XY 1 . This concern is an issue relating to the evaluation of hypotheses (e.g. applying statistics to the evaluation), which will require additional assumptions relating to how to evaluate the hypotheses. Strategies to deal with this apply some correction or penalization for multiple statistical testing [ 49 ] or partial pooling and regularizing priors [ 50 , 51 ]. These strategies aim to evaluate a broader variable selection ( x 1 or x 2 ) on equal or similar terms to a narrow variable selection ( x 1 ).

4.4. Pipeline selection

Scientific studies require decisions about how to perform the analysis. This scope considers transformations applied to the raw data ( XY raw ) to achieve some derivative ( XY ). These decisions can also involve selection procedures that drop observations deemed unreliable, standardizing, correcting confounding variables, or different philosophies. We can call the array of decisions and transformations used as the pipeline . A hypothesis varies in the number of pipelines:

• H 1 : XY has a relationship(s) R with pipeline p 1 .
• H 2 : XY has a relationship(s) R with pipeline p 1 or pipeline p 2 .
• H 3 : XY has a relationship(s) R with pipeline p 1 or pipeline p 2 , or pipeline p 3 .

Importantly, the pipeline here considers decisions regarding how the hypothesis shapes the data collection and transformation. We do not consider this to include decisions made regarding the assumptions relating to the statistical inference as those relate to operationalizing the evaluation of the hypothesis and not part of the hypothesis being evaluated (these assumptions are like auxiliary hypotheses, which are assumed to be true but not explicitly evaluated).

Like with variable selection ( XY ) and relationship selection ( R ), we can see that pipelines impact the scope of hypotheses. Again, we can symbolize the pipeline selection with a set P . As previously, | P | will denote the dimension of the pipeline selection. In the case of pipeline selection, we are testing the same variables, looking for the same relationship, but processing the variables or relationships with different pipelines to evaluate the relationship. Consequently, | P H1 | < | P H2 | < | P H3 |.

These issues regarding pipelines have received attention as the ‘garden of forking paths' [ 52 ]. Here, there are calls for researchers to ensure that their entire pipeline has been specified. Additionally, recent work has highlighted the diversity of results based on multiple analytical pipelines [ 53 , 54 ]. These results are often considered a concern, leading to calls that results should be pipeline resistant.

The wish for pipeline-resistant methods entails that hypotheses, in their narrowest form, are possible for all pipelines. Consequently, a narrower formulation will entail that this should not impact the hypothesis regardless of which pipeline is chosen. Thus the conjunction of pipelines is narrower than single pipelines. Consider the following three scenarios:

• H 3 : XY has a relationship(s) R with pipeline p 1 and pipeline p 2 .

In this instance, since H 1 is always true if H 3 is true, thus H 3 is a narrower formulation than H 1 . Consequently, | P H3 | < | P H1 | < | P H2 |. Decreasing the scope of the pipeline dimension also entails the increase in conjunction of pipelines (i.e. creating pipeline-resistant methods) rather than just the reduction of disjunctional statements.

4.5. Combining the dimensions

In summary, we then have three different dimensions that independently affect the scope of the hypothesis. We have demonstrated the following general claim regarding hypotheses:

• The variables XY have a relationship R with pipeline P .

And that the broadness and narrowness of a hypothesis depend on how large the three sets XY , R and P are. With this formulation, we can conclude that hypotheses have a scope that can be determined with a 3-tuple argument of (| R |, | XY |, | P |).

While hypotheses can be formulated along these three dimensions and generally aim to be reduced, it does not entail that these dimensions behave identically. For example, the relationship dimensions aim to reduce the number of elements as far as possible (e.g. to an interval). Contrastingly, for both variables and pipeline, the narrower hypothesis can reduce to single variables/pipelines or become narrower still and become conjunctions where all variables/pipelines need to corroborate the hypothesis (i.e. regardless of which method one follows, the hypothesis is correct).

5.  Additional possible dimensions

No commitment is being made about the exhaustive nature of there only being three dimensions that specify the hypothesis scope. Other dimensions may exist that specify the scope of a hypothesis. For example, one might consider the pipeline dimension as two different dimensions. The first would consider the experimental pipeline dimension regarding all variables relating to the experimental setup to collect data, and the latter would be the analytical pipeline dimension regarding the data analysis of any given data snapshot. Another possible dimension is adding the number of situations or contexts under which the hypothesis is valid. For example, any restraint such as ‘in a vacuum’, ‘under the speed of light’, or ‘in healthy human adults' could be considered an additional dimension of the hypothesis. There is no objection to whether these should be additional dimensions of the hypothesis. However, as stated above, these usually follow from the boundary conditions of the theory.

6.  Specifying the scope versus assumptions

We envision that this framework can help hypothesis-makers formulate hypotheses (in research plans, registered reports, preregistrations etc.). Further, using this framework while formulating hypotheses can help distinguish between auxiliary hypotheses and parts of the scientific hypothesis being tested. When writing preregistrations, it can frequently occur that some step in the method has two alternatives (e.g. a preprocessing step), and there is not yet reason to choose one over the other, and the researcher needs to make a decision. These following scenarios are possible:

• 1. Narrow pipeline scope . The researcher evaluates the hypothesis with both pipeline variables (i.e. H holds for both p 1 and p 2 where p 1 and p 2 can be substituted with each other in the pipeline).
• 2. Broad pipeline scope. The researcher evaluates the hypothesis with both pipeline variables, and only one needs to be correct (i.e. H holds for either p 1 or p 2 where p 1 and p 2 can be substituted with each other in the pipeline). The result of this experiment may help motivate choosing either p 1 or p 2 in future studies.
• 3. Auxiliary hypothesis. Based on some reason (e.g. convention), the researcher assumes p 1 and evaluates H assuming p 1 is true.

Here we see that the same pipeline step can be part of either the auxiliary hypotheses or the pipeline scope. This distinction is important because if (3) is chosen, the decision becomes an assumption that is not explicitly tested by the hypothesis. Consequently, a researcher confident in the hypothesis may state that the auxiliary hypothesis p 1 was incorrect, and they should retest their hypothesis using different assumptions. In the cases where this decision is part of the pipeline scope, the hypothesis is intertwined with this decision, removing the eventual wiggle-room to reject auxiliary hypotheses that were assumed. Furthermore, starting with broader pipeline hypotheses that gradually narrow down can lead to a more well-motivated protocol for approaching the problem. Thus, this framework can help researchers while writing their hypotheses in, for example, preregistrations because they can consider when they are committing to a decision, assuming it, or when they should perhaps test a broader hypothesis with multiple possible options (discussed in more detail in §11 below).

7.  The reduction of scope in hypothesis space

Having established that different scopes of a hypothesis are possible, we now consider how the hypotheses change over time. In this section, we consider how the scope of the hypothesis develops ideally within science.

Consider a new research question. A large number of hypotheses are possible. Let us call this set of all possible hypotheses the hypothesis space . Hypotheses formulated within this space can be narrower or broader based on the dimensions discussed previously ( figure 3 ).

Example of hypothesis space. The hypothesis scope is expressed as cuboids in three dimensions (relationship ( R ), variable ( XY ), pipeline ( P )). The hypothesis space is the entire possible space within the three dimensions. Three hypotheses are shown in the hypothesis space (H 1 , H 2 , H 3 ). H 2 and H 3 are subsets of H 1 .

After the evaluation of the hypothesis with the scientific process, the hypothesis will be accepted or rejected. 9 The evaluation could be done through falsification or via verification, depending on the philosophy of science commitments. Thereafter, other narrower formulations of the hypothesis can be formulated by reducing the relationship, variable or pipeline scope. If a narrower hypothesis is accepted, more specific details about the subject matter are known, or a theory has been refined in greater detail. A narrower hypothesis will entail a more specific relationship, variable or pipeline detailed in the hypothesis. Consequently, hypotheses linked to each other in this way will become narrower over time along one or more dimensions. Importantly, considering that the conjunction of elements is narrower than single elements for pipelines and variables, this process of narrower hypotheses will lead to more general hypotheses (i.e. they have to be applied in all conditions and yield less flexibility when they do not apply). 10

Considering that the scopes of hypotheses were defined as sets above, some properties can be deduced from this framework about how narrower hypotheses relate to broader hypotheses. Let us consider three hypotheses (H 1 , H 2 , and H 3 ; figure 3 ). H 2 and H 3 are non-overlapping subsets of H 1 . Thus H 2 and H 3 are both narrower in scope than H 1 . Thus the following is correct:

• P1: If H 1 is false, then H 2 is false, and H 2 does not need to be evaluated.
• P2: If H 2 is true, then the broader H 1 is true, and H 1 does not need to be evaluated.
• P3: If H 1 is true and H 2 is false, some other hypothesis H 3 of similar scope to H 2 is possible.

For example, suppose H 1 is ‘there is a relationship between x and y ’, H 2 is ‘there is a positive relationship between x and y ’, and H 3 is ‘a negative relationship between x and y ’. In that case, it becomes apparent how each of these follows. 11 Logically, many deductions from set theory are possible but will not be explored here. Instead, we will discuss two additional consequences of hypothesis scopes: scientific novelty and applications for the researcher who formulates a hypothesis.

P1–P3 have been formulated as hypotheses being true or false. In practice, hypotheses are likely evaluated probabilistically (e.g. ‘H 1 is likely’ or ‘there is evidence in support of H 1 ’). In these cases, P1–P3 can be rephrased to account for this by substituting true/false with statements relating to evidence. For example, P2 could read: ‘If there is evidence in support of H 2 , then there is evidence in support of H 1 , and H 1 does not need to be evaluated’.

8.  Scientific novelty as the reduction of scope

Novelty is a key concept that repeatedly occurs in multiple aspects of the scientific enterprise, from funding to publishing [ 55 ]. Generally, scientific progress establishes novel results based on some new hypothesis. Consequently, the new hypothesis for the novel results must be narrower than previously established knowledge (i.e. the size of the scopes is reduced). Otherwise, the result is trivial and already known (see P2 above). Thus, scientific work is novel if the scientific process produces a result based on hypotheses with either a smaller | R |, | XY |, or | P | compared to previous work.

This framework of dimensions of the scope of a hypothesis helps to demarcate when a hypothesis and the subsequent result are novel. If previous studies have established evidence for R 1 (e.g. there is a positive relationship between x and y ), a hypothesis will be novel if and only if it is narrower than R 1 . Thus, if R 2 is narrower in scope than R 1 (i.e. | R 2 | < | R 1 |), R 2 is a novel hypothesis.

Consider the following example. Study 1 hypothesizes, ‘There is a positive relationship between x and y ’. It identifies a linear relationship of 0.6. Next, Study 2 hypothesizes, ‘There is a specific linear relationship between x and y that is 0.6’. Study 2 also identifies the relationship of 0.6. Since this was a narrower hypothesis, Study 2 is novel despite the same result. Frequently, researchers claim that they are the first to demonstrate a relationship. Being the first to demonstrate a relationship is not the final measure of novelty. Having a narrower hypothesis than previous researchers is a sign of novelty as it further reduces the hypothesis space.

Finally, it should be noted that novelty is not the only objective of scientific work. Other attributes, such as improving the certainty of a current hypothesis (e.g. through replications), should not be overlooked. Additional scientific explanations and improved theories are other aspects. Additionally, this definition of novelty relating to hypothesis scope does not exclude other types of novelty (e.g. new theories or paradigms).

9.  How broad should a hypothesis be?

Given the previous section, it is elusive to conclude that the hypothesis should be as narrow as possible as it entails maximal knowledge gain and scientific novelty when formulating hypotheses. Indeed, many who advocate for daring or risky tests seem to hold this opinion. For example, Meehl [ 46 ] argues that we should evaluate theories based on point (or interval) prediction, which would be compatible with very narrow versions of relationships. We do not necessarily think that this is the most fruitful approach. In this section, we argue that hypotheses should aim to be narrower than current knowledge , but too narrow may be problematic .

Let us consider the idea of confirmatory analyses. These studies will frequently keep the previous hypothesis scopes regarding P and XY but aim to become more specific regarding R (i.e. using the same method and the same variables to detect a more specific relationship). A very daring or narrow hypothesis is to minimize R to include the fewest possible relationships. However, it becomes apparent that simply pursuing specificness or daringness is insufficient for selecting relevant hypotheses. Consider a hypothetical scenario where a researcher believes virtual reality use leads people to overestimate the amount of exercise they have done. If unaware of previous studies on this project, an apt hypothesis is perhaps ‘increased virtual reality usage correlates with a less accuracy of reported exercise performed’ (i.e. R is broad). However, a more specific and more daring hypothesis would be to specify the relationship further. Thus, despite not knowing if there is a relationship at all, a more daring hypothesis could be: ‘for every 1 h of virtual reality usage, there will be, on average, a 0.5% decrease in the accuracy of reported exercise performed’ (i.e. R is narrow). We believe it would be better to establish the broader hypothesis in any scenario here for the first experiment. Otherwise, if we fail to confirm the more specific formulation, we could reformulate another equally narrow relative to the broader hypothesis. This process of tweaking a daring hypothesis could be pursued ad infinitum . Such a situation will neither quickly identify the true hypothesis nor effectively use limited research resources.

By first discounting a broader hypothesis that there is no relationship, it will automatically discard all more specific formulations of that relationship in the hypothesis space. Returning to figure 3 , it will be better to establish H 1 before attempting H 2 or H 3 to ensure the correct area in the hypothesis space is being investigated. To provide an analogy: when looking for a needle among hay, first identify which farm it is at, then which barn, then which haystack, then which part of the haystack it is at before we start picking up individual pieces of hay. Thus, it is preferable for both pragmatic and cost-of-resource reasons to formulate sufficiently broad hypotheses to navigate the hypothesis space effectively.

Conversely, formulating too broad a relationship scope in a hypothesis when we already have evidence for narrower scope would be superfluous research (unless the evidence has been called into question by, for example, not being replicated). If multiple studies have supported the hypothesis ‘there is a 20-fold decrease in mortality after taking some medication M’, it would be unnecessary to ask, ‘Does M have any effect?’.

Our conclusion is that the appropriate scope of a hypothesis, and its three dimensions, follow a Goldilocks-like principle where too broad is superfluous and not novel, while too narrow is unnecessary or wasteful. Considering the scope of one's hypothesis and how it relates to previous hypotheses' scopes ensures one is asking appropriate questions.

Finally, there has been a recent trend in psychology that hypotheses should be formal [ 38 , 56 – 60 ]. Formal theories are precise since they are mathematical formulations entailing that their interpretations are clear (non-ambiguous) compared to linguistic theories. However, this literature on formal theories often refers to ‘precise predictions’ and ‘risky testing’ while frequently referencing Meehl, who advocates for narrow hypotheses (e.g. [ 38 , 56 , 59 ]). While perhaps not intended by any of the proponents, one interpretation of some of these positions is that hypotheses derived from formal theories will be narrow hypotheses (i.e. the quality of being ‘precise’ can mean narrow hypotheses with risky tests and non-ambiguous interpretations simultaneously). However, the benefit from the clarity (non-ambiguity) that formal theories/hypotheses bring also applies to broad formal hypotheses as well. They can include explicit but formalized versions of uncertain relationships, multiple possible pipelines, and large sets of variables. For example, a broad formal hypothesis can contain a hyperparameter that controls which distribution the data fit (broad relationship scope), or a variable could represent a set of formalized explicit pipelines (broad pipeline scope) that will be tested. In each of these instances, it is possible to formalize non-ambiguous broad hypotheses from broad formal theories that do not yet have any justification for being overly narrow. In sum, our argumentation here stating that hypotheses should not be too narrow is not an argument against formal theories but rather that hypotheses (derived from formal theories) do not necessarily have to be narrow.

10.  Other approaches to categorizing hypotheses

The framework we present here is a way of categorizing hypotheses into (at least) three dimensions regarding the hypothesis scope, which we believe is accessible to researchers and help link scientific work over time while also trying to remain neutral with regard to a specific philosophy of science. Our proposal does not aim to be antagonistic or necessarily contradict other categorizing schemes—but we believe that our framework provides benefits.

One recent categorization scheme is the Theoretical (T), Auxiliary (A), Statistical (S) and Inferential (I) assumption model (together becoming the TASI model) [ 61 , 62 ]. Briefly, this model considers theory to generate theoretical hypotheses. To translate from theoretical unobservable terms (e.g. personality, anxiety, mass), auxiliary assumptions are needed to generate an empirical hypothesis. Statistical assumptions are often needed to test the empirical hypothesis (e.g. what is the distribution, is it skewed or not) [ 61 , 62 ]. Finally, additional inferential assumptions are needed to generalize to a larger population (e.g. was there a random and independent sampling from defined populations). The TASI model is insightful and helpful in highlighting the distance between a theory and the observation that would corroborate/contradict it. Part of its utility is to bring auxiliary hypotheses into the foreground, to improve comparisons between studies and improve theory-based interventions [ 63 , 64 ].

We do agree with the importance of being aware of or stating the auxiliary hypotheses, but there are some differences between the frameworks. First, the number of auxiliary assumptions in TASI can be several hundred [ 62 ], whereas our framework will consider some of them as part of the pipeline dimension. Consider the following four assumptions: ‘the inter-stimulus interval is between 2000 ms and 3000 ms', ‘the data will be z-transformed’, ‘subjects will perform correctly’, and ‘the measurements were valid’. According to the TASI model, all these will be classified similarly as auxiliary assumptions. Contrarily, within our framework, it is possible to consider the first two as part of the pipeline dimension and the latter two as auxiliary assumptions, and consequently, the first two become integrated as part of the hypothesis being tested and the latter two auxiliary assumptions. A second difference between the frameworks relates to non-theoretical studies (convenience, applied or atheoretical). Our framework allows for the possibility that the hypothesis space generated by theoretical and convenience studies can interact and inform each other within the same framework . Contrarily, in TASI, the theory assumptions no longer apply, and a different type of hypothesis model is needed; these assumptions must be replaced by another group of assumptions (where ‘substantive application assumptions' replace the T and the A, becoming SSI) [ 61 ]. Finally, part of our rationale for our framework is to be able to link and track hypotheses and hypothesis development together over time, so our classification scheme has different utility.

Another approach which has some similar utility to this framework is theory construction methodology (TCM) [ 57 ]. The similarity here is that TCM aims to be a practical guide to improve theory-making in psychology. It is an iterative process which relates theory, phenomena and data. Here hypotheses are not an explicit part of the model. However, what is designated as ‘proto theory’ could be considered a hypothesis in our framework as they are a product of abduction, shaping the theory space. Alternatively, what is deduced to evaluate the theory can also be considered a hypothesis. We consider both possible and that our framework can integrate with these two steps, especially since TCM does not have clear guidelines for how to do each step.

11.  From theory to practice: implementing this framework

We believe that many practising researchers can relate to many aspects of this framework. But, how can a researcher translate the above theoretical framework to their work? The utility of this framework lies in bringing these three scopes of a hypothesis together and explaining how each can be reduced. We believe researchers can use this framework to describe their current practices more clearly. Here we discuss how it can be helpful for researchers when formulating, planning, preregistering, and discussing the evaluation of their scientific hypotheses. These practical implications are brief, and future work can expand on the connection between the full interaction between hypothesis space and scope. Furthermore, both authors have the most experience in cognitive neuroscience, and some of the practical implications may revolve around this type of research and may not apply equally to other fields.

11.1. Helping to form hypotheses

Abduction, according to Peirce, is a hypothesis-making exercise [ 22 , 26 – 28 ]. Given some observations, a general testable explanation of the phenomena is formed. However, when making the hypothesis, this statement will have a scope (either explicitly or implicitly). Using our framework, the scope can become explicit. The hypothesis-maker can start with ‘The variables XY have a relationship R with pipeline P ’ as a scaffold to form the hypothesis. From here, the hypothesis-maker can ‘fill in the blanks’, explicitly adding each of the scopes. Thus, when making a hypothesis via abduction and using our framework, the hypothesis will have an explicit scope when it is made. By doing this, there is less chance that a formulated hypothesis is unclear, ambiguous, and needs amending at a later stage.

11.2. Assisting to clearly state hypotheses

A hypothesis is not just formulated but also communicated. Hypotheses are stated in funding applications, preregistrations, registered reports, and academic articles. Further, preregistered hypotheses are often omitted or changed in the final article [ 11 ], and hypotheses are not always explicitly stated in articles [ 12 ]. How can this framework help to make better hypotheses? Similar to the previous point, filling in the details of ‘The variables XY have a relationship R with pipeline P ’ is an explicit way to communicate the hypothesis. Thinking about each of these dimensions should entail an appropriate explicit scope and, hopefully, less variation between preregistered and reported hypotheses. The hypothesis does not need to be a single sentence, and details of XY and P will often be developed in the methods section of the text. However, using this template as a starting point can help ensure the hypothesis is stated, and the scope of all three dimensions has been communicated.

11.3. Helping to promote explicit and broad hypotheses instead of vague hypotheses

There is an important distinction between vague hypotheses and broad hypotheses, and this framework can help demarcate between them. A vague statement would be: ‘We will quantify depression in patients after treatment’. Here there is uncertainty relating to how the researcher will go about doing the experiment (i.e. how will depression be quantified?). However, a broad statement can be uncertain, but the uncertainty is part of the hypothesis: ‘Two different mood scales (S 1 or S 2 ) will be given to patients and test if only one (or both) changed after treatment’. This latter statement is transparently saying ‘S 1 or S 2 ’ is part of a broad hypothesis—the uncertainty is whether the two different scales are quantifying the same construct. We keep this uncertainty within the broad hypothesis, which will get evaluated, whereas a vague hypothesis has uncertainty as part of the interpretation of the hypothesis. This framework can be used when formulating hypotheses to help be broad (where needed) but not vague.

11.4. Which hypothesis should be chosen?

When considering the appropriate scope above, we argued for a Goldilocks-like principle of determining the hypothesis that is not too broad or too narrow. However, when writing, for example, a preregistration, how does one identify this sweet spot? There is no easy or definite universal answer to this question. However, one possible way is first to identify the XY , R , and P of previous hypotheses. From here, identify what a non-trivial step is to improve our knowledge of the research area. So, for example, could you be more specific about the exact nature of the relationship between the variables? Does the pipeline correspond to today's scientific standards, or were some suboptimal decisions made? Is there another population that you think the previous result also applies to? Do you think that maybe a more specific construct or subpopulation might explain the previous result? Could slightly different constructs (perhaps easier to quantify) be used to obtain a similar relationship? Are there even more constructs to which this relationship should apply simultaneously? Are you certain of the direction of the relationship? Answering affirmatively to any of these questions will likely make a hypothesis narrower and connect to previous research while being clear and explicit. Moreover, depending on the research question, answering any of these may be sufficiently narrow to be a non-trivial innovation. However, there are many other ways to make a hypothesis narrower than these guiding questions.

11.5. The confirmatory–exploratory continuum

Research is often dichotomized into confirmatory (testing a hypothesis) or exploratory (without a priori hypotheses). With this framework, researchers can consider how their research acts on some hypothesis space. Confirmatory and exploratory work has been defined in terms of how each interacts with the researcher's degrees of freedom (where confirmatory aims to reduce while exploratory utilizes them [ 30 ]). Both broad confirmatory and narrow exploratory research are possible using this definition and possible within this framework. How research interacts with the hypothesis space helps demarcate it. For example, if a hypothesis reduces the scope, it becomes more confirmatory, and trying to understand data given the current scope would be more exploratory work. This further could help demarcate when exploration is useful. Future theoretical work can detail how different types of research impact the hypothesis space in more detail.

11.6. Understanding when multiverse analyses are needed

Researchers writing a preregistration may face many degrees of freedom they have to choose from, and different researchers may motivate different choices. If, when writing such a preregistration, there appears to be little evidential support for certain degrees of freedom over others, the researcher is left with the option to either make more auxiliary assumptions or identify when an investigation into the pipeline scope is necessary by conducting a multiverse analysis that tests the impact of the different degrees of freedom on the result (see [ 8 ]). Thus, when applying this framework to explicitly state what pipeline variables are part of the hypothesis or an auxiliary assumption, the researcher can identify when it might be appropriate to conduct a multiverse analysis because they are having difficulty formulating hypotheses.

11.7. Describing novelty

Academic journals and research funders often ask for novelty, but the term ‘novelty’ can be vague and open to various interpretations [ 55 ]. This framework can be used to help justify the novelty of research. For example, consider a scenario where a previous study has established a psychological construct (e.g. well-being) that correlates with a certain outcome measure (e.g. long-term positive health outcomes). This framework can be used to explicitly justify novelty by (i) providing a more precise understanding of the relationship (e.g. linear or linear–plateau) or (ii) identifying more specific variables related to well-being or health outcomes. Stating how some research is novel is clearer than merely stating that the work is novel. This practice might even help journals and funders identify what type of novelty they would like to reward. In sum, this framework can help identify and articulate how research is novel.

11.8. Help to identify when standardization of pipelines is beneficial or problematic to a field

Many consider standardization in a field to be important for ensuring the comparability of results. Standardization of methods and tools entails that the pipeline P is identical (or at least very similar) across studies. However, in such cases, the standardized pipeline becomes an auxiliary assumption representing all possible pipelines. Therefore, while standardized pipelines have their benefits, this assumption becomes broader without validating (e.g. via multiverse analysis) which pipelines a standardized P represents. In summary, because this framework helps distinguish between auxiliary assumptions and explicit parts of the hypothesis and identifies when a multiverse analysis is needed, it can help determine when standardizations of pipelines are representative (narrower hypotheses) or assumptive (broader hypotheses).

12.  Conclusion

Here, we have argued that the scope of a hypothesis is made up of three dimensions: the relationship ( R ), variable ( XY ) and pipeline ( P ) selection. Along each of these dimensions, the scope can vary. Different types of scientific enterprises will often have hypotheses that vary the size of the scopes. We have argued that this focus on the scope of the hypothesis along these dimensions helps the hypothesis-maker formulate their hypotheses for preregistrations while also helping demarcate auxiliary hypotheses (assumed to be true) from the hypothesis (those being evaluated during the scientific process).

Hypotheses are an essential part of the scientific process. Considering what type of hypothesis is sufficient or relevant is an essential job of the researcher that we think has been overlooked. We hope this work promotes an understanding of what a hypothesis is and how its formulation and reduction in scope is an integral part of scientific progress. We hope it also helps clarify how broad hypotheses need not be vague or inappropriate.

Finally, we applied this idea of scopes to scientific progress and considered how to formulate an appropriate hypothesis. We have also listed several ways researchers can practically implement this framework today. However, there are other practicalities of this framework that future work should explore. For example, it could be used to differentiate and demarcate different scientific contributions (e.g. confirmatory studies, exploration studies, validation studies) with how their hypotheses interact with the different dimensions of the hypothesis space. Further, linking hypotheses over time within this framework can be a foundation for open hypothesis-making by promoting explicit links to previous work and detailing the reduction of the hypothesis space. This framework helps quantify the contribution to the hypothesis space of different studies and helps clarify what aspects of hypotheses can be relevant at different times.

Acknowledgements

We thank Filip Gedin, Kristoffer Sundberg, Jens Fust, and James Steele for valuable feedback on earlier versions of this article. We also thank Mark Rubin and an unnamed reviewer for valuable comments that have improved the article.

1 While this is our intention, we cannot claim that every theory has been accommodated.

2 Similar requirements of science being able to evaluate the hypothesis can be found in pragmatism [ 22 ], logical positivism [ 23 ] and falsification [ 24 ].

3 Although when making inferences about a failed evaluation of a scientific hypothesis it is possible, due to underdetermination, to reject the auxiliary hypothesis instead of rejecting the hypothesis. However, that rejection occurs at a later inference stage. The evaluation using the scientific method aims to test the scientific hypothesis, not the auxiliary assumptions.

4 Although some have argued that this practice is not as problematic or questionable (see [ 34 , 35 ]).

5 Alternatively, theories sometimes expand their boundary conditions. A theory that was previously about ‘humans' can be used with a more inclusive boundary condition. Thus it is possible for the hypothesis-maker to use a theory about humans (decision making) and expand it to fruit flies or plants (see [ 43 ]).

6 A similarity exists here with Popper, where he uses set theory in a similar way to compare theories (not hypotheses). Popper also discusses how theories with overlapping sets but neither is a subset are also comparable (see [ 24 , §§32–34]). We do not exclude this possibility but can require additional assumptions.

7 When this could be unclear, we place the element within quotation marks.

8 Here, we have assumed that there is no interaction between these variables in variable selection. If an interaction between x 1 and x 2 is hypothesized, this should be viewed as a different variable compared to ‘ x 1 or x 2 ’. The motivation behind this is because the hypothesis ‘ x 1 or x 2 ’ is not a superset of the interaction (i.e. ‘ x 1 or x 2 ’ is not necessarily true when the interaction is true). The interaction should, in this case, be considered a third variable (e.g. I( x 1 , x 2 )) and the hypothesis ‘ x 1 or x 2 or I( x 1 , x 2 )’ is broader than ‘ x 1 or x 2 ’.

9 Or possibly ambiguous or inconclusive.

10 This formulation of scope is compatible with different frameworks from the philosophy of science. For example, by narrowing the scope would in a Popperian terminology mean prohibiting more basic statements (thus a narrower hypothesis has a higher degree of falsifiability). The reduction of scope in the relational dimension would in Popperian terminology mean increase in precision (e.g. a circle is more precise than an ellipse since circles are a subset of possible ellipses), whereas reduction in variable selection and pipeline dimension would mean increase universality (e.g. ‘all heavenly bodies' is more universal than just ‘planets') [ 24 ]. For Meehl the reduction of the relationship dimension would amount to decreasing the relative tolerance of a theory to the Spielraum [ 46 ] .

11 If there is no relationship between x and y , we do not need to test if there is a positive relationship. If we know there is a positive relationship between x and y , we do not need to test if there is a relationship. If we know there is a relationship but there is not a positive relationship, then it is possible that they have a negative relationship.

Data accessibility

Declaration of ai use.

We have not used AI-assisted technologies in creating this article.

Authors' contributions

W.H.T.: conceptualization, investigation, writing—original draft, writing—review and editing; S.S.: investigation, writing—original draft, writing—review and editing.

Both authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

We received no funding for this study.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.4: Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 283

• David Diez, Christopher Barr, & Mine Çetinkaya-Rundel
• OpenIntro Statistics

Is the typical US runner getting faster or slower over time? We consider this question in the context of the Cherry Blossom Run, comparing runners in 2006 and 2012. Technological advances in shoes, training, and diet might suggest runners would be faster in 2012. An opposing viewpoint might say that with the average body mass index on the rise, people tend to run slower. In fact, all of these components might be influencing run time.

In addition to considering run times in this section, we consider a topic near and dear to most students: sleep. A recent study found that college students average about 7 hours of sleep per night.15 However, researchers at a rural college are interested in showing that their students sleep longer than seven hours on average. We investigate this topic in Section 4.3.4.

Hypothesis Testing Framework

The average time for all runners who finished the Cherry Blossom Run in 2006 was 93.29 minutes (93 minutes and about 17 seconds). We want to determine if the run10Samp data set provides strong evidence that the participants in 2012 were faster or slower than those runners in 2006, versus the other possibility that there has been no change. 16 We simplify these three options into two competing hypotheses :

• H 0 : The average 10 mile run time was the same for 2006 and 2012.
• H A : The average 10 mile run time for 2012 was different than that of 2006.

We call H 0 the null hypothesis and H A the alternative hypothesis.

Null and alternative hypotheses

• The null hypothesis (H 0 ) often represents either a skeptical perspective or a claim to be tested.
• The alternative hypothesis (H A ) represents an alternative claim under consideration and is often represented by a range of possible parameter values.

15 theloquitur.com/?p=1161

16 While we could answer this question by examining the entire population data (run10), we only consider the sample data (run10Samp), which is more realistic since we rarely have access to population data.

The null hypothesis often represents a skeptical position or a perspective of no difference. The alternative hypothesis often represents a new perspective, such as the possibility that there has been a change.

Hypothesis testing framework

The skeptic will not reject the null hypothesis (H 0 ), unless the evidence in favor of the alternative hypothesis (H A ) is so strong that she rejects H 0 in favor of H A .

The hypothesis testing framework is a very general tool, and we often use it without a second thought. If a person makes a somewhat unbelievable claim, we are initially skeptical. However, if there is sufficient evidence that supports the claim, we set aside our skepticism and reject the null hypothesis in favor of the alternative. The hallmarks of hypothesis testing are also found in the US court system.

Exercise \(\PageIndex{1}\)

A US court considers two possible claims about a defendant: she is either innocent or guilty. If we set these claims up in a hypothesis framework, which would be the null hypothesis and which the alternative? 17

Jurors examine the evidence to see whether it convincingly shows a defendant is guilty. Even if the jurors leave unconvinced of guilt beyond a reasonable doubt, this does not mean they believe the defendant is innocent. This is also the case with hypothesis testing: even if we fail to reject the null hypothesis, we typically do not accept the null hypothesis as true. Failing to find strong evidence for the alternative hypothesis is not equivalent to accepting the null hypothesis.

17 H 0 : The average cost is $650 per month, \(\mu\) = $650.

In the example with the Cherry Blossom Run, the null hypothesis represents no difference in the average time from 2006 to 2012. The alternative hypothesis represents something new or more interesting: there was a difference, either an increase or a decrease. These hypotheses can be described in mathematical notation using \(\mu_{12}\) as the average run time for 2012:

• H 0 : \(\mu_{12} = 93.29\)
• H A : \(\mu_{12} \ne 93.29\)

where 93.29 minutes (93 minutes and about 17 seconds) is the average 10 mile time for all runners in the 2006 Cherry Blossom Run. Using this mathematical notation, the hypotheses can now be evaluated using statistical tools. We call 93.29 the null value since it represents the value of the parameter if the null hypothesis is true. We will use the run10Samp data set to evaluate the hypothesis test.

Testing Hypotheses using Confidence Intervals

We can start the evaluation of the hypothesis setup by comparing 2006 and 2012 run times using a point estimate from the 2012 sample: \(\bar {x}_{12} = 95.61\) minutes. This estimate suggests the average time is actually longer than the 2006 time, 93.29 minutes. However, to evaluate whether this provides strong evidence that there has been a change, we must consider the uncertainty associated with \(\bar {x}_{12}\).

1 6 The jury considers whether the evidence is so convincing (strong) that there is no reasonable doubt regarding the person's guilt; in such a case, the jury rejects innocence (the null hypothesis) and concludes the defendant is guilty (alternative hypothesis).

We learned in Section 4.1 that there is fluctuation from one sample to another, and it is very unlikely that the sample mean will be exactly equal to our parameter; we should not expect \(\bar {x}_{12}\) to exactly equal \(\mu_{12}\). Given that \(\bar {x}_{12} = 95.61\), it might still be possible that the population average in 2012 has remained unchanged from 2006. The difference between \(\bar {x}_{12}\) and 93.29 could be due to sampling variation, i.e. the variability associated with the point estimate when we take a random sample.

In Section 4.2, confidence intervals were introduced as a way to find a range of plausible values for the population mean. Based on run10Samp, a 95% confidence interval for the 2012 population mean, \(\mu_{12}\), was calculated as

\[(92.45, 98.77)\]

Because the 2006 mean, 93.29, falls in the range of plausible values, we cannot say the null hypothesis is implausible. That is, we failed to reject the null hypothesis, H 0 .

Double negatives can sometimes be used in statistics

In many statistical explanations, we use double negatives. For instance, we might say that the null hypothesis is not implausible or we failed to reject the null hypothesis. Double negatives are used to communicate that while we are not rejecting a position, we are also not saying it is correct.

Example \(\PageIndex{1}\)

Next consider whether there is strong evidence that the average age of runners has changed from 2006 to 2012 in the Cherry Blossom Run. In 2006, the average age was 36.13 years, and in the 2012 run10Samp data set, the average was 35.05 years with a standard deviation of 8.97 years for 100 runners.

First, set up the hypotheses:

• H 0 : The average age of runners has not changed from 2006 to 2012, \(\mu_{age} = 36.13.\)
• H A : The average age of runners has changed from 2006 to 2012, \(\mu _{age} 6 \ne 36.13.\)

We have previously veri ed conditions for this data set. The normal model may be applied to \(\bar {y}\) and the estimate of SE should be very accurate. Using the sample mean and standard error, we can construct a 95% con dence interval for \(\mu _{age}\) to determine if there is sufficient evidence to reject H 0 :

\[\bar{y} \pm 1.96 \times \dfrac {s}{\sqrt {100}} \rightarrow 35.05 \pm 1.96 \times 0.90 \rightarrow (33.29, 36.81)\]

This confidence interval contains the null value, 36.13. Because 36.13 is not implausible, we cannot reject the null hypothesis. We have not found strong evidence that the average age is different than 36.13 years.

Exercise \(\PageIndex{2}\)

Colleges frequently provide estimates of student expenses such as housing. A consultant hired by a community college claimed that the average student housing expense was $650 per month. What are the null and alternative hypotheses to test whether this claim is accurate? 18

H A : The average cost is different than $650 per month, \(\mu \ne\) $650.

18 Applying the normal model requires that certain conditions are met. Because the data are a simple random sample and the sample (presumably) represents no more than 10% of all students at the college, the observations are independent. The sample size is also sufficiently large (n = 75) and the data exhibit only moderate skew. Thus, the normal model may be applied to the sample mean.

Exercise \(\PageIndex{3}\)

The community college decides to collect data to evaluate the $650 per month claim. They take a random sample of 75 students at their school and obtain the data represented in Figure 4.11. Can we apply the normal model to the sample mean?

If the court makes a Type 1 Error, this means the defendant is innocent (H 0 true) but wrongly convicted. A Type 2 Error means the court failed to reject H 0 (i.e. failed to convict the person) when she was in fact guilty (H A true).

Example \(\PageIndex{2}\)

The sample mean for student housing is $611.63 and the sample standard deviation is $132.85. Construct a 95% confidence interval for the population mean and evaluate the hypotheses of Exercise 4.22.

The standard error associated with the mean may be estimated using the sample standard deviation divided by the square root of the sample size. Recall that n = 75 students were sampled.

\[ SE = \dfrac {s}{\sqrt {n}} = \dfrac {132.85}{\sqrt {75}} = 15.34\]

You showed in Exercise 4.23 that the normal model may be applied to the sample mean. This ensures a 95% confidence interval may be accurately constructed:

\[\bar {x} \pm z*SE \rightarrow 611.63 \pm 1.96 \times 15.34 \times (581.56, 641.70)\]

Because the null value $650 is not in the confidence interval, a true mean of $650 is implausible and we reject the null hypothesis. The data provide statistically significant evidence that the actual average housing expense is less than $650 per month.

Decision Errors

Hypothesis tests are not flawless. Just think of the court system: innocent people are sometimes wrongly convicted and the guilty sometimes walk free. Similarly, we can make a wrong decision in statistical hypothesis tests. However, the difference is that we have the tools necessary to quantify how often we make such errors.

There are two competing hypotheses: the null and the alternative. In a hypothesis test, we make a statement about which one might be true, but we might choose incorrectly. There are four possible scenarios in a hypothesis test, which are summarized in Table 4.12.

A Type 1 Error is rejecting the null hypothesis when H0 is actually true. A Type 2 Error is failing to reject the null hypothesis when the alternative is actually true.

Exercise 4.25

In a US court, the defendant is either innocent (H 0 ) or guilty (H A ). What does a Type 1 Error represent in this context? What does a Type 2 Error represent? Table 4.12 may be useful.

To lower the Type 1 Error rate, we might raise our standard for conviction from "beyond a reasonable doubt" to "beyond a conceivable doubt" so fewer people would be wrongly convicted. However, this would also make it more difficult to convict the people who are actually guilty, so we would make more Type 2 Errors.

Exercise 4.26

How could we reduce the Type 1 Error rate in US courts? What influence would this have on the Type 2 Error rate?

To lower the Type 2 Error rate, we want to convict more guilty people. We could lower the standards for conviction from "beyond a reasonable doubt" to "beyond a little doubt". Lowering the bar for guilt will also result in more wrongful convictions, raising the Type 1 Error rate.

Exercise 4.27

How could we reduce the Type 2 Error rate in US courts? What influence would this have on the Type 1 Error rate?

A skeptic would have no reason to believe that sleep patterns at this school are different than the sleep patterns at another school.

Exercises 4.25-4.27 provide an important lesson:

If we reduce how often we make one type of error, we generally make more of the other type.

Hypothesis testing is built around rejecting or failing to reject the null hypothesis. That is, we do not reject H 0 unless we have strong evidence. But what precisely does strong evidence mean? As a general rule of thumb, for those cases where the null hypothesis is actually true, we do not want to incorrectly reject H 0 more than 5% of the time. This corresponds to a significance level of 0.05. We often write the significance level using \(\alpha\) (the Greek letter alpha): \(\alpha = 0.05.\) We discuss the appropriateness of different significance levels in Section 4.3.6.

If we use a 95% confidence interval to test a hypothesis where the null hypothesis is true, we will make an error whenever the point estimate is at least 1.96 standard errors away from the population parameter. This happens about 5% of the time (2.5% in each tail). Similarly, using a 99% con dence interval to evaluate a hypothesis is equivalent to a significance level of \(\alpha = 0.01\).

A confidence interval is, in one sense, simplistic in the world of hypothesis tests. Consider the following two scenarios:

• The null value (the parameter value under the null hypothesis) is in the 95% confidence interval but just barely, so we would not reject H 0 . However, we might like to somehow say, quantitatively, that it was a close decision.
• The null value is very far outside of the interval, so we reject H 0 . However, we want to communicate that, not only did we reject the null hypothesis, but it wasn't even close. Such a case is depicted in Figure 4.13.

In Section 4.3.4, we introduce a tool called the p-value that will be helpful in these cases. The p-value method also extends to hypothesis tests where con dence intervals cannot be easily constructed or applied.

Formal Testing using p-Values

The p-value is a way of quantifying the strength of the evidence against the null hypothesis and in favor of the alternative. Formally the p-value is a conditional probability.

definition: p-value

The p-value is the probability of observing data at least as favorable to the alternative hypothesis as our current data set, if the null hypothesis is true. We typically use a summary statistic of the data, in this chapter the sample mean, to help compute the p-value and evaluate the hypotheses.

A poll by the National Sleep Foundation found that college students average about 7 hours of sleep per night. Researchers at a rural school are interested in showing that students at their school sleep longer than seven hours on average, and they would like to demonstrate this using a sample of students. What would be an appropriate skeptical position for this research?

This is entirely based on the interests of the researchers. Had they been only interested in the opposite case - showing that their students were actually averaging fewer than seven hours of sleep but not interested in showing more than 7 hours - then our setup would have set the alternative as \(\mu < 7\).

We can set up the null hypothesis for this test as a skeptical perspective: the students at this school average 7 hours of sleep per night. The alternative hypothesis takes a new form reflecting the interests of the research: the students average more than 7 hours of sleep. We can write these hypotheses as

• H 0 : \(\mu\) = 7.
• H A : \(\mu\) > 7.

Using \(\mu\) > 7 as the alternative is an example of a one-sided hypothesis test. In this investigation, there is no apparent interest in learning whether the mean is less than 7 hours. (The standard error can be estimated from the sample standard deviation and the sample size: \(SE_{\bar {x}} = \dfrac {s_x}{\sqrt {n}} = \dfrac {1.75}{\sqrt {110}} = 0.17\)). Earlier we encountered a two-sided hypothesis where we looked for any clear difference, greater than or less than the null value.

Always use a two-sided test unless it was made clear prior to data collection that the test should be one-sided. Switching a two-sided test to a one-sided test after observing the data is dangerous because it can inflate the Type 1 Error rate.

TIP: One-sided and two-sided tests

If the researchers are only interested in showing an increase or a decrease, but not both, use a one-sided test. If the researchers would be interested in any difference from the null value - an increase or decrease - then the test should be two-sided.

TIP: Always write the null hypothesis as an equality

We will find it most useful if we always list the null hypothesis as an equality (e.g. \(\mu\) = 7) while the alternative always uses an inequality (e.g. \(\mu \ne 7, \mu > 7, or \mu < 7)\).

The researchers at the rural school conducted a simple random sample of n = 110 students on campus. They found that these students averaged 7.42 hours of sleep and the standard deviation of the amount of sleep for the students was 1.75 hours. A histogram of the sample is shown in Figure 4.14.

Before we can use a normal model for the sample mean or compute the standard error of the sample mean, we must verify conditions. (1) Because this is a simple random sample from less than 10% of the student body, the observations are independent. (2) The sample size in the sleep study is sufficiently large since it is greater than 30. (3) The data show moderate skew in Figure 4.14 and the presence of a couple of outliers. This skew and the outliers (which are not too extreme) are acceptable for a sample size of n = 110. With these conditions veri ed, the normal model can be safely applied to \(\bar {x}\) and the estimated standard error will be very accurate.

What is the standard deviation associated with \(\bar {x}\)? That is, estimate the standard error of \(\bar {x}\). 25

The hypothesis test will be evaluated using a significance level of \(\alpha = 0.05\). We want to consider the data under the scenario that the null hypothesis is true. In this case, the sample mean is from a distribution that is nearly normal and has mean 7 and standard deviation of about 0.17. Such a distribution is shown in Figure 4.15.

The shaded tail in Figure 4.15 represents the chance of observing such a large mean, conditional on the null hypothesis being true. That is, the shaded tail represents the p-value. We shade all means larger than our sample mean, \(\bar {x} = 7.42\), because they are more favorable to the alternative hypothesis than the observed mean.

We compute the p-value by finding the tail area of this normal distribution, which we learned to do in Section 3.1. First compute the Z score of the sample mean, \(\bar {x} = 7.42\):

\[Z = \dfrac {\bar {x} - \text {null value}}{SE_{\bar {x}}} = \dfrac {7.42 - 7}{0.17} = 2.47\]

Using the normal probability table, the lower unshaded area is found to be 0.993. Thus the shaded area is 1 - 0.993 = 0.007. If the null hypothesis is true, the probability of observing such a large sample mean for a sample of 110 students is only 0.007. That is, if the null hypothesis is true, we would not often see such a large mean.

We evaluate the hypotheses by comparing the p-value to the significance level. Because the p-value is less than the significance level \((p-value = 0.007 < 0.05 = \alpha)\), we reject the null hypothesis. What we observed is so unusual with respect to the null hypothesis that it casts serious doubt on H 0 and provides strong evidence favoring H A .

p-value as a tool in hypothesis testing

The p-value quantifies how strongly the data favor H A over H 0 . A small p-value (usually < 0.05) corresponds to sufficient evidence to reject H 0 in favor of H A .

TIP: It is useful to First draw a picture to find the p-value

It is useful to draw a picture of the distribution of \(\bar {x}\) as though H 0 was true (i.e. \(\mu\) equals the null value), and shade the region (or regions) of sample means that are at least as favorable to the alternative hypothesis. These shaded regions represent the p-value.

The ideas below review the process of evaluating hypothesis tests with p-values:

• The null hypothesis represents a skeptic's position or a position of no difference. We reject this position only if the evidence strongly favors H A .
• A small p-value means that if the null hypothesis is true, there is a low probability of seeing a point estimate at least as extreme as the one we saw. We interpret this as strong evidence in favor of the alternative.
• We reject the null hypothesis if the p-value is smaller than the significance level, \(\alpha\), which is usually 0.05. Otherwise, we fail to reject H 0 .
• We should always state the conclusion of the hypothesis test in plain language so non-statisticians can also understand the results.

The p-value is constructed in such a way that we can directly compare it to the significance level ( \(\alpha\)) to determine whether or not to reject H 0 . This method ensures that the Type 1 Error rate does not exceed the significance level standard.

If the null hypothesis is true, how often should the p-value be less than 0.05?

About 5% of the time. If the null hypothesis is true, then the data only has a 5% chance of being in the 5% of data most favorable to H A .

Exercise 4.31

Suppose we had used a significance level of 0.01 in the sleep study. Would the evidence have been strong enough to reject the null hypothesis? (The p-value was 0.007.) What if the significance level was \(\alpha = 0.001\)? 27

27 We reject the null hypothesis whenever p-value < \(\alpha\). Thus, we would still reject the null hypothesis if \(\alpha = 0.01\) but not if the significance level had been \(\alpha = 0.001\).

Exercise 4.32

Ebay might be interested in showing that buyers on its site tend to pay less than they would for the corresponding new item on Amazon. We'll research this topic for one particular product: a video game called Mario Kart for the Nintendo Wii. During early October 2009, Amazon sold this game for $46.99. Set up an appropriate (one-sided!) hypothesis test to check the claim that Ebay buyers pay less during auctions at this same time. 28

28 The skeptic would say the average is the same on Ebay, and we are interested in showing the average price is lower.

Exercise 4.33

During early October, 2009, 52 Ebay auctions were recorded for Mario Kart.29 The total prices for the auctions are presented using a histogram in Figure 4.17, and we may like to apply the normal model to the sample mean. Check the three conditions required for applying the normal model: (1) independence, (2) at least 30 observations, and (3) the data are not strongly skewed. 30

30 (1) The independence condition is unclear. We will make the assumption that the observations are independent, which we should report with any nal results. (2) The sample size is sufficiently large: \(n = 52 \ge 30\). (3) The data distribution is not strongly skewed; it is approximately symmetric.

H 0 : The average auction price on Ebay is equal to (or more than) the price on Amazon. We write only the equality in the statistical notation: \(\mu_{ebay} = 46.99\).

H A : The average price on Ebay is less than the price on Amazon, \(\mu _{ebay} < 46.99\).

29 These data were collected by OpenIntro staff.

Example 4.34

The average sale price of the 52 Ebay auctions for Wii Mario Kart was $44.17 with a standard deviation of $4.15. Does this provide sufficient evidence to reject the null hypothesis in Exercise 4.32? Use a significance level of \(\alpha = 0.01\).

The hypotheses were set up and the conditions were checked in Exercises 4.32 and 4.33. The next step is to find the standard error of the sample mean and produce a sketch to help find the p-value.

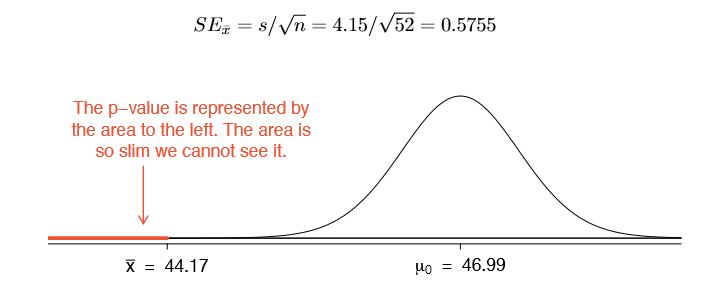
Because the alternative hypothesis says we are looking for a smaller mean, we shade the lower tail. We find this shaded area by using the Z score and normal probability table: \(Z = \dfrac {44.17 \times 46.99}{0.5755} = -4.90\), which has area less than 0.0002. The area is so small we cannot really see it on the picture. This lower tail area corresponds to the p-value.

Because the p-value is so small - specifically, smaller than = 0.01 - this provides sufficiently strong evidence to reject the null hypothesis in favor of the alternative. The data provide statistically signi cant evidence that the average price on Ebay is lower than Amazon's asking price.

Two-sided hypothesis testing with p-values

We now consider how to compute a p-value for a two-sided test. In one-sided tests, we shade the single tail in the direction of the alternative hypothesis. For example, when the alternative had the form \(\mu\) > 7, then the p-value was represented by the upper tail (Figure 4.16). When the alternative was \(\mu\) < 46.99, the p-value was the lower tail (Exercise 4.32). In a two-sided test, we shade two tails since evidence in either direction is favorable to H A .

Exercise 4.35 Earlier we talked about a research group investigating whether the students at their school slept longer than 7 hours each night. Let's consider a second group of researchers who want to evaluate whether the students at their college differ from the norm of 7 hours. Write the null and alternative hypotheses for this investigation. 31

Example 4.36 The second college randomly samples 72 students and nds a mean of \(\bar {x} = 6.83\) hours and a standard deviation of s = 1.8 hours. Does this provide strong evidence against H 0 in Exercise 4.35? Use a significance level of \(\alpha = 0.05\).

First, we must verify assumptions. (1) A simple random sample of less than 10% of the student body means the observations are independent. (2) The sample size is 72, which is greater than 30. (3) Based on the earlier distribution and what we already know about college student sleep habits, the distribution is probably not strongly skewed.

Next we can compute the standard error \((SE_{\bar {x}} = \dfrac {s}{\sqrt {n}} = 0.21)\) of the estimate and create a picture to represent the p-value, shown in Figure 4.18. Both tails are shaded.

31 Because the researchers are interested in any difference, they should use a two-sided setup: H 0 : \(\mu\) = 7, H A : \(\mu \ne 7.\)

An estimate of 7.17 or more provides at least as strong of evidence against the null hypothesis and in favor of the alternative as the observed estimate, \(\bar {x} = 6.83\).

We can calculate the tail areas by rst nding the lower tail corresponding to \(\bar {x}\):

\[Z = \dfrac {6.83 - 7.00}{0.21} = -0.81 \xrightarrow {table} \text {left tail} = 0.2090\]

Because the normal model is symmetric, the right tail will have the same area as the left tail. The p-value is found as the sum of the two shaded tails:

\[ \text {p-value} = \text {left tail} + \text {right tail} = 2 \times \text {(left tail)} = 0.4180\]

This p-value is relatively large (larger than \(\mu\)= 0.05), so we should not reject H 0 . That is, if H 0 is true, it would not be very unusual to see a sample mean this far from 7 hours simply due to sampling variation. Thus, we do not have sufficient evidence to conclude that the mean is different than 7 hours.

Example 4.37 It is never okay to change two-sided tests to one-sided tests after observing the data. In this example we explore the consequences of ignoring this advice. Using \(\alpha = 0.05\), we show that freely switching from two-sided tests to onesided tests will cause us to make twice as many Type 1 Errors as intended.

Suppose the sample mean was larger than the null value, \(\mu_0\) (e.g. \(\mu_0\) would represent 7 if H 0 : \(\mu\) = 7). Then if we can ip to a one-sided test, we would use H A : \(\mu > \mu_0\). Now if we obtain any observation with a Z score greater than 1.65, we would reject H 0 . If the null hypothesis is true, we incorrectly reject the null hypothesis about 5% of the time when the sample mean is above the null value, as shown in Figure 4.19.

Suppose the sample mean was smaller than the null value. Then if we change to a one-sided test, we would use H A : \(\mu < \mu_0\). If \(\bar {x}\) had a Z score smaller than -1.65, we would reject H 0 . If the null hypothesis is true, then we would observe such a case about 5% of the time.

By examining these two scenarios, we can determine that we will make a Type 1 Error 5% + 5% = 10% of the time if we are allowed to swap to the "best" one-sided test for the data. This is twice the error rate we prescribed with our significance level: \(\alpha = 0.05\) (!).

Caution: One-sided hypotheses are allowed only before seeing data

After observing data, it is tempting to turn a two-sided test into a one-sided test. Avoid this temptation. Hypotheses must be set up before observing the data. If they are not, the test must be two-sided.

Choosing a Significance Level

Choosing a significance level for a test is important in many contexts, and the traditional level is 0.05. However, it is often helpful to adjust the significance level based on the application. We may select a level that is smaller or larger than 0.05 depending on the consequences of any conclusions reached from the test.

• If making a Type 1 Error is dangerous or especially costly, we should choose a small significance level (e.g. 0.01). Under this scenario we want to be very cautious about rejecting the null hypothesis, so we demand very strong evidence favoring H A before we would reject H 0 .
• If a Type 2 Error is relatively more dangerous or much more costly than a Type 1 Error, then we should choose a higher significance level (e.g. 0.10). Here we want to be cautious about failing to reject H 0 when the null is actually false. We will discuss this particular case in greater detail in Section 4.6.

Significance levels should reflect consequences of errors

The significance level selected for a test should reflect the consequences associated with Type 1 and Type 2 Errors.

Example 4.38

A car manufacturer is considering a higher quality but more expensive supplier for window parts in its vehicles. They sample a number of parts from their current supplier and also parts from the new supplier. They decide that if the high quality parts will last more than 12% longer, it makes nancial sense to switch to this more expensive supplier. Is there good reason to modify the significance level in such a hypothesis test?

The null hypothesis is that the more expensive parts last no more than 12% longer while the alternative is that they do last more than 12% longer. This decision is just one of the many regular factors that have a marginal impact on the car and company. A significancelevel of 0.05 seems reasonable since neither a Type 1 or Type 2 error should be dangerous or (relatively) much more expensive.

Example 4.39

The same car manufacturer is considering a slightly more expensive supplier for parts related to safety, not windows. If the durability of these safety components is shown to be better than the current supplier, they will switch manufacturers. Is there good reason to modify the significance level in such an evaluation?

The null hypothesis would be that the suppliers' parts are equally reliable. Because safety is involved, the car company should be eager to switch to the slightly more expensive manufacturer (reject H 0 ) even if the evidence of increased safety is only moderately strong. A slightly larger significance level, such as \(\mu = 0.10\), might be appropriate.

Exercise 4.40

A part inside of a machine is very expensive to replace. However, the machine usually functions properly even if this part is broken, so the part is replaced only if we are extremely certain it is broken based on a series of measurements. Identify appropriate hypotheses for this test (in plain language) and suggest an appropriate significance level. 32

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

Hypothesis testing.

Key Topics:

• Basic approach
• Null and alternative hypothesis
• Decision making and the p -value
• Z-test & Nonparametric alternative

Basic approach to hypothesis testing

• State a model describing the relationship between the explanatory variables and the outcome variable(s) in the population and the nature of the variability. State all of your assumptions .
• Specify the null and alternative hypotheses in terms of the parameters of the model.
• Invent a test statistic that will tend to be different under the null and alternative hypotheses.
• Using the assumptions of step 1, find the theoretical sampling distribution of the statistic under the null hypothesis of step 2. Ideally the form of the sampling distribution should be one of the “standard distributions”(e.g. normal, t , binomial..)
• Calculate a p -value , as the area under the sampling distribution more extreme than your statistic. Depends on the form of the alternative hypothesis.
• Choose your acceptable type 1 error rate (alpha) and apply the decision rule : reject the null hypothesis if the p-value is less than alpha, otherwise do not reject.
• \(\frac{\bar{X}-\mu_0}{\sigma / \sqrt{n}}\)
• general form is: (estimate - value we are testing)/(st.dev of the estimate)
• z-statistic follows N(0,1) distribution
• 2 × the area above |z|, area above z,or area below z, or
• compare the statistic to a critical value, |z| ≥ z α/2 , z ≥ z α , or z ≤ - z α
• Choose the acceptable level of Alpha = 0.05, we conclude …. ?

Making the Decision

It is either likely or unlikely that we would collect the evidence we did given the initial assumption. (Note: “likely” or “unlikely” is measured by calculating a probability!)

If it is likely , then we “ do not reject ” our initial assumption. There is not enough evidence to do otherwise.

If it is unlikely , then:

• either our initial assumption is correct and we experienced an unusual event or,
• our initial assumption is incorrect

In statistics, if it is unlikely, we decide to “ reject ” our initial assumption.

Example: Criminal Trial Analogy

First, state 2 hypotheses, the null hypothesis (“H 0 ”) and the alternative hypothesis (“H A ”)

• H 0 : Defendant is not guilty.
• H A : Defendant is guilty.

Usually the H 0 is a statement of “no effect”, or “no change”, or “chance only” about a population parameter.

While the H A , depending on the situation, is that there is a difference, trend, effect, or a relationship with respect to a population parameter.

• It can one-sided and two-sided.
• In two-sided we only care there is a difference, but not the direction of it. In one-sided we care about a particular direction of the relationship. We want to know if the value is strictly larger or smaller.

Then, collect evidence, such as finger prints, blood spots, hair samples, carpet fibers, shoe prints, ransom notes, handwriting samples, etc. (In statistics, the data are the evidence.)

Next, you make your initial assumption.

• Defendant is innocent until proven guilty.

In statistics, we always assume the null hypothesis is true .

Then, make a decision based on the available evidence.

• If there is sufficient evidence (“beyond a reasonable doubt”), reject the null hypothesis . (Behave as if defendant is guilty.)
• If there is not enough evidence, do not reject the null hypothesis . (Behave as if defendant is not guilty.)

If the observed outcome, e.g., a sample statistic, is surprising under the assumption that the null hypothesis is true, but more probable if the alternative is true, then this outcome is evidence against H 0 and in favor of H A .

An observed effect so large that it would rarely occur by chance is called statistically significant (i.e., not likely to happen by chance).

Using the p -value to make the decision

The p -value represents how likely we would be to observe such an extreme sample if the null hypothesis were true. The p -value is a probability computed assuming the null hypothesis is true, that the test statistic would take a value as extreme or more extreme than that actually observed. Since it's a probability, it is a number between 0 and 1. The closer the number is to 0 means the event is “unlikely.” So if p -value is “small,” (typically, less than 0.05), we can then reject the null hypothesis.

Significance level and p -value

Significance level, α, is a decisive value for p -value. In this context, significant does not mean “important”, but it means “not likely to happened just by chance”.

α is the maximum probability of rejecting the null hypothesis when the null hypothesis is true. If α = 1 we always reject the null, if α = 0 we never reject the null hypothesis. In articles, journals, etc… you may read: “The results were significant ( p <0.05).” So if p =0.03, it's significant at the level of α = 0.05 but not at the level of α = 0.01. If we reject the H 0 at the level of α = 0.05 (which corresponds to 95% CI), we are saying that if H 0 is true, the observed phenomenon would happen no more than 5% of the time (that is 1 in 20). If we choose to compare the p -value to α = 0.01, we are insisting on a stronger evidence!

So, what kind of error could we make? No matter what decision we make, there is always a chance we made an error.

Errors in Criminal Trial:

Errors in Hypothesis Testing

Type I error (False positive): The null hypothesis is rejected when it is true.

• α is the maximum probability of making a Type I error.

Type II error (False negative): The null hypothesis is not rejected when it is false.

• β is the probability of making a Type II error

There is always a chance of making one of these errors. But, a good scientific study will minimize the chance of doing so!

The power of a statistical test is its probability of rejecting the null hypothesis if the null hypothesis is false. That is, power is the ability to correctly reject H 0 and detect a significant effect. In other words, power is one minus the type II error risk.

\(\text{Power }=1-\beta = P\left(\text{reject} H_0 | H_0 \text{is false } \right)\)

Which error is worse?

Type I = you are innocent, yet accused of cheating on the test. Type II = you cheated on the test, but you are found innocent.

This depends on the context of the problem too. But in most cases scientists are trying to be “conservative”; it's worse to make a spurious discovery than to fail to make a good one. Our goal it to increase the power of the test that is to minimize the length of the CI.

We need to keep in mind:

• the effect of the sample size,
• the correctness of the underlying assumptions about the population,
• statistical vs. practical significance, etc…

(see the handout). To study the tradeoffs between the sample size, α, and Type II error we can use power and operating characteristic curves.

What type of error might we have made?

Type I error is claiming that average student height is not 65 inches, when it really is. Type II error is failing to claim that the average student height is not 65in when it is.

We rejected the null hypothesis, i.e., claimed that the height is not 65, thus making potentially a Type I error. But sometimes the p -value is too low because of the large sample size, and we may have statistical significance but not really practical significance! That's why most statisticians are much more comfortable with using CI than tests.

There is a need for a further generalization. What if we can't assume that σ is known? In this case we would use s (the sample standard deviation) to estimate σ.

If the sample is very large, we can treat σ as known by assuming that σ = s . According to the law of large numbers, this is not too bad a thing to do. But if the sample is small, the fact that we have to estimate both the standard deviation and the mean adds extra uncertainty to our inference. In practice this means that we need a larger multiplier for the standard error.

We need one-sample t -test.

One sample t -test

• Assume data are independently sampled from a normal distribution with unknown mean μ and variance σ 2 . Make an initial assumption, μ 0 .
• t-statistic: \(\frac{\bar{X}-\mu_0}{s / \sqrt{n}}\) where s is a sample st.dev.
• t-statistic follows t -distribution with df = n - 1
• Alpha = 0.05, we conclude ….

Testing for the population proportion

Let's go back to our CNN poll. Assume we have a SRS of 1,017 adults.

We are interested in testing the following hypothesis: H 0 : p = 0.50 vs. p > 0.50

What is the test statistic?

If alpha = 0.05, what do we conclude?

We will see more details in the next lesson on proportions, then distributions, and possible tests.

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, a complete guide on hypothesis testing in statistics, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.

All You Need to Know About Bias in Statistics

A Complete Guide to Get a Grasp of Time Series Analysis

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is hypothesis testing in statistics types and examples.

Lesson 10 of 24 By Avijeet Biswal

Table of Contents

In today’s data-driven world , decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life - 

• A teacher assumes that 60% of his college's students come from lower-middle-class families.
• A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternate Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average. 

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

 We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps of Hypothesis Testing

Step 1: specify your null and alternate hypotheses.

It is critical to rephrase your original research hypothesis (the prediction that you wish to study) as a null (Ho) and alternative (Ha) hypothesis so that you can test it quantitatively. Your first hypothesis, which predicts a link between variables, is generally your alternate hypothesis. The null hypothesis predicts no link between the variables of interest.

Step 2: Gather Data

For a statistical test to be legitimate, sampling and data collection must be done in a way that is meant to test your hypothesis. You cannot draw statistical conclusions about the population you are interested in if your data is not representative.

Step 3: Conduct a Statistical Test

Other statistical tests are available, but they all compare within-group variance (how to spread out the data inside a category) against between-group variance (how different the categories are from one another). If the between-group variation is big enough that there is little or no overlap between groups, your statistical test will display a low p-value to represent this. This suggests that the disparities between these groups are unlikely to have occurred by accident. Alternatively, if there is a large within-group variance and a low between-group variance, your statistical test will show a high p-value. Any difference you find across groups is most likely attributable to chance. The variety of variables and the level of measurement of your obtained data will influence your statistical test selection.

Step 4: Determine Rejection Of Your Null Hypothesis

Your statistical test results must determine whether your null hypothesis should be rejected or not. In most circumstances, you will base your judgment on the p-value provided by the statistical test. In most circumstances, your preset level of significance for rejecting the null hypothesis will be 0.05 - that is, when there is less than a 5% likelihood that these data would be seen if the null hypothesis were true. In other circumstances, researchers use a lower level of significance, such as 0.01 (1%). This reduces the possibility of wrongly rejecting the null hypothesis.

Step 5: Present Your Results 

The findings of hypothesis testing will be discussed in the results and discussion portions of your research paper, dissertation, or thesis. You should include a concise overview of the data and a summary of the findings of your statistical test in the results section. You can talk about whether your results confirmed your initial hypothesis or not in the conversation. Rejecting or failing to reject the null hypothesis is a formal term used in hypothesis testing. This is likely a must for your statistics assignments.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

Chi-Square 

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

• The null hypothesis is (H0 <= 90) or less change.
• A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true]. 

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Level of Significance

The alpha value is a criterion for determining whether a test statistic is statistically significant. In a statistical test, Alpha represents an acceptable probability of a Type I error. Because alpha is a probability, it can be anywhere between 0 and 1. In practice, the most commonly used alpha values are 0.01, 0.05, and 0.1, which represent a 1%, 5%, and 10% chance of a Type I error, respectively (i.e. rejecting the null hypothesis when it is in fact correct).

Future-Proof Your AI/ML Career: Top Dos and Don'ts

A p-value is a metric that expresses the likelihood that an observed difference could have occurred by chance. As the p-value decreases the statistical significance of the observed difference increases. If the p-value is too low, you reject the null hypothesis.

Here you have taken an example in which you are trying to test whether the new advertising campaign has increased the product's sales. The p-value is the likelihood that the null hypothesis, which states that there is no change in the sales due to the new advertising campaign, is true. If the p-value is .30, then there is a 30% chance that there is no increase or decrease in the product's sales.  If the p-value is 0.03, then there is a 3% probability that there is no increase or decrease in the sales value due to the new advertising campaign. As you can see, the lower the p-value, the chances of the alternate hypothesis being true increases, which means that the new advertising campaign causes an increase or decrease in sales.

Why is Hypothesis Testing Important in Research Methodology?

Hypothesis testing is crucial in research methodology for several reasons:

• Provides evidence-based conclusions: It allows researchers to make objective conclusions based on empirical data, providing evidence to support or refute their research hypotheses.
• Supports decision-making: It helps make informed decisions, such as accepting or rejecting a new treatment, implementing policy changes, or adopting new practices.
• Adds rigor and validity: It adds scientific rigor to research using statistical methods to analyze data, ensuring that conclusions are based on sound statistical evidence.
• Contributes to the advancement of knowledge: By testing hypotheses, researchers contribute to the growth of knowledge in their respective fields by confirming existing theories or discovering new patterns and relationships.

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

• It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
• Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
• Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
• Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore Simplilearn’s Post Graduate Program in Data Science.

If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is hypothesis testing and its types?

Hypothesis testing is a statistical method used to make inferences about a population based on sample data. It involves formulating two hypotheses: the null hypothesis (H0), which represents the default assumption, and the alternative hypothesis (Ha), which contradicts H0. The goal is to assess the evidence and determine whether there is enough statistical significance to reject the null hypothesis in favor of the alternative hypothesis.

Types of hypothesis testing:

• One-sample test: Used to compare a sample to a known value or a hypothesized value.
• Two-sample test: Compares two independent samples to assess if there is a significant difference between their means or distributions.
• Paired-sample test: Compares two related samples, such as pre-test and post-test data, to evaluate changes within the same subjects over time or under different conditions.
• Chi-square test: Used to analyze categorical data and determine if there is a significant association between variables.
• ANOVA (Analysis of Variance): Compares means across multiple groups to check if there is a significant difference between them.

3. What are the steps of hypothesis testing?

The steps of hypothesis testing are as follows:

• Formulate the hypotheses: State the null hypothesis (H0) and the alternative hypothesis (Ha) based on the research question.
• Set the significance level: Determine the acceptable level of error (alpha) for making a decision.
• Collect and analyze data: Gather and process the sample data.
• Compute test statistic: Calculate the appropriate statistical test to assess the evidence.
• Make a decision: Compare the test statistic with critical values or p-values and determine whether to reject H0 in favor of Ha or not.
• Draw conclusions: Interpret the results and communicate the findings in the context of the research question.

4. What are the 2 types of hypothesis testing?

• One-tailed (or one-sided) test: Tests for the significance of an effect in only one direction, either positive or negative.
• Two-tailed (or two-sided) test: Tests for the significance of an effect in both directions, allowing for the possibility of a positive or negative effect.

The choice between one-tailed and two-tailed tests depends on the specific research question and the directionality of the expected effect.

5. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

• Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
• Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
• Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

• Português Br
• Journalist Pass

What you need to know if you test positive or negative for COVID-19

Share this:.

Are you waiting for your COVID-19 test results and wonder what you need to do next? Mayo Clinic COVID-19 diagnostic experts provide some helpful guidelines to walk you through the next steps. It all depends on the type of test and your results.

Next steps after testing positive with polymerase chain reaction test

If you test positive for COVID-19 using a polymerase chain reaction, or PCR, test, follow these guidelines, based on  Centers for Disease Control and Prevention  guidelines, to determine what you need to do:

• Isolate for at least five days. You can end isolation after five full days if you are fever-free for 24 hours without the use of fever-reducing medication and your other symptoms have improved. Day 0 is your first day of symptoms. NOTE: You should also check with your employer, school district or public health department for exact isolation guidelines for you and/or your family if you test positive for COVID-19 as those guidelines may be different.
• If you test positive for COVID-19 and never develop symptoms, commonly referred to as being asymptomatic, isolate for at least five days and wear a mask around others at home. Day 0 is the day the sample was collected for a positive test result.
• Contact your health care team to let them know you tested positive for COVID-19 so it can be documented in your health record. 
• At the end of isolation, wear a properly fitted surgical/procedural mask in public settings.
• If you still have a fever, regardless of how many days you've been in isolation, continue to stay home and monitor your symptoms until you no longer have a fever.
• You may need to have a negative COVID-19 test result, either a PCR or at-home antigen test before you can return to work or school. Check with your employer, school district or public health department to determine if this is needed.

If you test negative for COVID-19 using a PCR test, you are likely not infected, provided you do not have any symptoms.

If you do not have symptoms of COVID-19 and do not have a known exposure to a person infected with COVID-19, you do not need to quarantine. Continue to wear a surgical/procedural mask in all public settings.

Next steps after testing positive with at-home antigen test

If you take an at-home COVID-19 antigen test and your results indicate you are positive for COVID-19, Mayo Clinic answers some common questions to help determine your next steps.

Can I trust the results of an at-home antigen test?

If you have symptoms of COVID-19, take an at-home antigen test and it is positive, you likely have COVID-19 and should isolate at home according to Centers for Disease Control and Prevention guidelines.

Sometimes an at-home COVID-19 antigen test can have a false-negative result. A negative at-home test is not a free pass if the person taking the test has symptoms.

If you use an at-home test that comes back negative, and you do have symptoms that persist or get worse, it’s a good idea to get a lab-based PCR test for COVID-19 and influenza. You also should stay home and isolate until you get the PCR test results back. The antigen test may have missed an early infection.

How long do I need to stay in isolation if I test positive for COVID-19 using an at-home antigen test? Is isolation time the same for a PCR test?

Generally, if you are positive for COVID-19 by either the antigen or PCR test, you will need to be in isolation for a minimum of five days from the onset of your symptoms and/or a positive test for COVID-19.

Do I need to have another PCR COVID-19 test completed before I return to work or normal activity following the five days of isolation?

You may need to have a negative COVID-19 test result, either by a PCR or at-home antigen test, before you can return to work or school, depending on specific requirements for the organization and where you live.

Should I let my local health care team know I tested positive for COVID-19 with an at-home antigen COVID-19 test?

Yes. You should let your local care team know that you tested positive for COVID-19 using an at-home antigen test. This will ensure your care team can help you with any COVID-19 related care needs if you continue to have prolonged symptoms of COVID-19 or if you need to seek additional care related to COVID-19.

Do I need to take another at-home COVID-19 antigen test to make sure I'm negative after a certain amount of time to make sure I no longer have COVID-19 before I return to normal activity?

No. If you no longer have symptoms after five days or are fever-free for at least 24 hours without using a fever-reducing medication, you do not need to take another COVID-19 test to confirm you are no longer positive, unless you have been directed to by your workplace or school. However, if your symptoms persist longer than five days, you should remain isolated until you no longer have symptoms for at least 24 hours.

Does my entire household need to be tested to make sure they are not positive following my positive at-home COVID-19 antigen test?

No. If others in your household do not have any COVID-19 symptoms, they do not need to be tested. However, if they experience symptoms, they also should be tested.

If someone in my family also tests positive using an at-home COVID-19 antigen test, do I need to quarantine again even though I've already had a positive COVID-19 diagnosis?

If you have a member in your household that tests positive for COVID-19, and you also tested positive for COVID-19  within the last 90 days, you do not need to quarantine, according to guidance from the  CDC .

For a PDF version of the test chart.

Information in this post was accurate at the time of its posting. Due to the fluid nature of the COVID-19 pandemic, scientific understanding, along with guidelines and recommendations, may have changed since the original publication date . 

For more information and all your COVID-19 coverage, go to the  Mayo Clinic News Network  and  mayoclinic.org .

Learn more about  tracking COVID-19 and COVID-19 trends .

• Study finds that patients with alcohol-associated cirrhosis have worse outcomes in recovering from critical illness, compared with other cirrhosis patients Mayo Clinic Minute: Exercising in the new year

Related Articles

• Type 2 Diabetes
• Heart Disease
• Digestive Health
• Multiple Sclerosis
• COVID-19 Vaccines
• Occupational Therapy
• Healthy Aging
• Health Insurance
• Public Health
• Patient Rights
• Caregivers & Loved Ones
• End of Life Concerns
• Health News
• Thyroid Test Analyzer
• Doctor Discussion Guides
• Hemoglobin A1c Test Analyzer
• Lipid Test Analyzer
• Complete Blood Count (CBC) Analyzer
• What to Buy
• Editorial Process
• Meet Our Medical Expert Board

If You’re Over 65, You May Not Need These Common Medical Tests and Screenings

skynesher / Getty Images

Key Takeaways

• Older adults who seek healthcare are at risk for overtreatment and having screenings that they don’t need.
• Many common medical tests are not recommended after a certain age or if you’re not having symptoms.
• Patients should ask their healthcare provider to explain why a test is recommended and speak up if they aren’t sure why it’s needed.

After the age of 65, many people find themselves in a healthcare provider’s office more frequently for help with managing a chronic disease or just to “keep an eye on” their health. Since having access to quality healthcare in the United States is not a given, being proactive about your health if you’re able is generally a smart move.

That said, there can be such a thing as too much of a good thing—even when it comes to medical care. Many older adults don’t realize that some routine screenings and treatments may not be necessary and can even be harmful for them.

A recent study highlighted the need for safeguards to avoid overtreating older adult patients, which can include unnecessary tests and screenings, particularly for prostate cancer (PSA test), urinary tract infections (UTI), and diabetes.

The study concluded that decision support tool interventions like electronic alerts and warnings helped providers reduce incidents of unnecessary PSA testing by 9% and UTI screenings by 5.5%. They also made providers aware of when tests they’d ordered for a patient may not be needed.  

“This shows that alerts like the ones used in this study can help curtail overuse of tests and treatments,” study lead author Stephen Persell, MD, MPH , professor of medicine at Northwestern University Feinberg School of Medicine, told Verywell. “We are always getting continuing education as clinicians. This type of nudge can help remind us of things we’ve learned previously when it is directly relevant to a patient we are working with.”

What Are the Risks of Over Treating Older Adults?

Ordering a simple screening or adjusting a treatment plan may not sound like a big deal, but it can actually have negative health consequences down the road for older adults. It can also be expensive, time-consuming, and stressful.

Take a routine screening for a UTI . Many older women naturally have bacteria in their bladders that can cause a UTI test to come back positive. However, just having the bacteria in their urinary tract doesn’t mean it’s causing an active infection—especially if they don’t have any symptoms.

When a patient with no symptoms gets a positive screening, it may lead to an antibiotic prescription that’s not needed, but that could come with side effects like nausea, diarrhea, and dizziness. Big picture, prescribing antibiotics that patients don’t need contributes to antibiotic resistance —an already big and growing problem.

Prostate cancer screenings are another common example. One study found that PSA testing in men over the age of 69 often results in false positives, which leads to invasive procedures and side effects from treatment. That’s part of why the U.S. Preventive Services Task Force (USPSTF) recommends against PSA screenings for men aged 70 years and older.

Another risk for older adults is the health negative consequences of overtreating diabetes. While it is important to closely manage blood sugar levels, glycemic control needs to be modified as people get older and their bodies change.

Katherine Ward, MD , a board-certified geriatrician with Stanford Senior Care, told Verywell that diabetes management guidelines should be loosened for older adults because they have an increased risk of hypoglycemia (low blood sugar), which can be a life-threatening emergency. 

“There is a lot of awareness that some tests and treatments in medicine are used in clinical situations where they haven’t been shown to be beneficial,” said Persell. “At best, it is likely that doing the tests hasn’t been shown to add value. At worst, they can potentially lead to downstream harms.”

Which Treatment and Screenings Should Be Modified for Older Adults—or Avoided?

Experts say there are other common medical tests that could be modified in older adults or even skipped for some patients. Providers have to weigh the benefits against the possible harms in each case. The decision to screen or not should be based on a patient’s health history, current physical health, and life expectancy.

Common medical tests and screenings that older adults might not need include:

• Colonoscopy  
• Anxiety screenings
• Type 2 diabetes screenings

“There are thousands of tests out there,” said Ward. “But if the patient is not having any symptoms, it is probably not necessary. Screening or testing for older adults should only be done if a doctor thinks a disease might be present.” 

Which Health Screenings Are Highly Recommended for Older Adults?

While there might be some tests and screenings that older adults don't need, that doesn’t mean they should forgo routine medical care. They should have annual well visits and physicals and ask their provider about getting routine screenings and vaccinations that are recommended for the older adult population:

• High blood pressure
• Cholesterol levels
• Vision and hearing exam
• Bone density scan (DEXA scan)
• Influenza vaccine
• COVID vaccine
• Pneumococcal vaccine
• RSV vaccine

What Can Providers Do?

Students don’t get a lot of training in geriatric care in medical school, according to Ward. As a result, many primary care providers are not well-versed in treating older adults. That lack of knowledge could be contributing to the overtreatment of their older patients.

To help combat the problem, the researchers behind the latest study offered providers who took part in the study education and embedded alerts in the electronic medical record system. The warnings popped up if the provider ordered a treatment that wasn’t not recommended for the age group. The researchers found that these interventions resulted in a significant reduction of older adults getting care that didn’t have any added benefit for their health.

Another active initiative to help providers and patients discuss what tests are necessary and which ones may not be is the Choosing Wisely campaign. The campaign lists 45 examples of common tests or treatments that don’t have strong supporting evidence behind them.

“I think it’s important for clinicians to think several steps ahead when choosing tests,” said Persell. “We always need to ask ourselves—how will these results change what I do? Is it likely that pursuing the results of a positive test will benefit this patient? And does the medical evidence support what I’m doing?”

Providers aren’t the only ones who can ask questions, though. Patients should speak up if they don’t understand why a test is being ordered or a screening is being recommended. If your provider wants you to have a test or screening, ask them why. Find out what the benefits and risks are and why they think it’s important for your health.

What This Means For You

Older adults may be getting over-screened with common medical tests that don’t offer much benefit and may even be harmful. Asking your provider to explain why a test or screening is recommended creates an honest, open dialogue that can help you avoid getting medical treatments that you don’t need.

Persell SD, Petito LC, Lee JY, et al. Reducing care overuse in older patients using professional norms and accountability: a cluster randomized controlled trial . Ann Intern Med . Published online February 6, 2024. doi:10.7326/M23-2183

Medicalxpress. Reducing harmful health screenings and overtreatment in older adults .

Cortes-Penfield NW, Trautner BW, Jump RLP. Urinary tract infection and asymptomatic bacteriuria in older adults . Infect Dis Clin North Am . 2017;31(4):673-688. doi:10.1016/j.idc.2017.07.002

US Preventive Services Task Force, Grossman DC, Curry SJ, et al. Screening for prostate cancer: US Preventive Services Task Force recommendation statement . JAMA . 2018;319(18):1901-1913. doi:10.1001/jama.2018.3710

Kalavacherla S, Riviere P, Javier-DesLoges J, et al. Low-value prostate-specific antigen screening in older males . JAMA Netw Open. 2023;6(4):e237504. doi:10.1001/jamanetworkopen.2023.7504

U.S. Preventive Services Task Force. A & B recommendations .

Centers for Disease Control and Prevention. Older adults now able to receive additional dose of updated COVID-19 vaccine .

American Academy of Family Physicians. Preventive care for seniors .

By Amy Isler, RN, MSN, CSN Amy Isler, RN, MSN, CSN, is a registered nurse with over six years of patient experience. She is a credentialed school nurse in California.

• Manage Account
• Election Results
• Solar Eclipse
• Bleeding Out
• Things to Do
• Public Notices
• Help Center

sports Rangers

What do Texas Rangers need to win multiple titles? Super-agent Scott Boras has some ideas

Boras, who represents free agent pitcher jordan montgomery, says a litmus test usually follows a franchise’s first championship.

By Evan Grant

5:34 PM on Mar 12, 2024 CDT

SURPRISE, Ariz. — If there is one thing Scott Boras has learned over more than 40 years of negotiating baseball contracts, it’s not to tell a billionaire owner what to do.

He takes a slightly different approach.

He talks about what other billionaire owners are willing to do to win championships.

Which is how Tuesday’s conversation with the super-agent, ostensibly about the Texas Rangers and the stagnant pitching market, suddenly turned to … Jim Crane.

Be the smartest Rangers fan. Get the latest news.

By signing up you agree to our  Terms of Service  and  Privacy Policy

Billionaire owner of the Astros.

The guy whose bid to buy the Rangers out of bankruptcy failed .

“I give Jim Crane and [Dodgers owner] Mark Walter a lot of credit,” Boras said, on his way to making a point about the potential fit for a reunion between the Rangers and his still-unemployed client Jordan Montgomery . “They have created modern-day franchises that optimize both winning and revenue enhancement.

“[Crane] made the commitments to make Houston competitive through multiple World Series runs and seven ALCS’ in a row. Those are the kinds of franchises that will go down as most respected and most revered franchises in baseball.”

Hang on. He’s getting there.

“There always comes a litmus test for a franchise and it usually comes after the first world championship,” Boras said. “If you sustain that championship level, you build the kind of legacy that few do. The Dodgers and Astros, for example, have always made the kind of move that is most difficult — the last one to a championship level for that season and beyond. It’s the kind of move that requires some [financial] flexibility in the moment; however it’s the kind of move that separates them from one-and-done champs to championship legacy.”

And there it is: The sermon. Without any of the shlocky, but adored, puns that mark his winter media tour.

The message: If you want to win multiple championships as the Rangers have stated, you can’t stop making moves. Because others won’t.

Now, all of this coming from Boras on March 12 — let’s see here, uh, 16 days before the season opens — may sound to you a little like desperation. Maybe it is. Montgomery, a Rangers’ postseason hero last year and Blake Snell, the NL Cy Young Award winner in 2023, give the Boras Training Institute, which is a real thing, as good a 1-2 punch as any rotation in baseball. Montgomery has been throwing live BPs there. Up to 65 pitches on Tuesday. In case anybody was wondering. They are, however, both still unsigned by MLB teams.

Even so, being desperate and being right aren’t necessarily mutually exclusive. Both can be true. Just as both these factors can be true: Rangers owner Ray Davis has gone further financially than ever before and the team’s payroll has barely changed from last year.

For the record, for Competitive Balance Tax purposes the Rangers finished 2023 at $242 million, according to Baseball Prospectus’ payroll database, and is currently estimated at $243.8 million.

The Astros, by adding Josh Hader among other changes, have jumped from $226 million to $248 million. The Braves have jumped $17 million to $265 million. The Phillies, Yankees and Dodgers. Up, up and away. The Rangers have gone further than ever before. Other teams have gone even further. And none of those teams took home the $27-30 million extra revenue that Boras estimates comes along with winning a World Series.

Again, a skeptic might say it’s rich to hear Boras say all this with two unsigned clients who could fill the Rangers’ most glaring need: More starting pitching depth. If that wasn’t abundantly clear last week, it should be more so now with Owen White, Cole Winn and Zak Kent all among the first waves of minor league cuts . The message sent to the pitchers was pretty straightforward. They aren’t ready. But maybe a subtle message to ownership as well that help, if needed, is not on hand.

To that end, more spending isn’t always the only answer. There are other methods. The Rangers, according to a person with knowledge of the club’s thinking, have been considering what it would take to trade for Chicago White Sox starter Dylan Cease. White Sox scouts have descended in droves upon Rangers camp this week.

Cease, who also happens to be a Boras client, has been pitching this spring like an ace, is under control through 2025 and will only make $8 million this year. On the other hand, he’d probably cost a significant amount of talent inventory. And the market for him might be hotter than the free agents. The Yankees, concerned about Gerrit Cole’s elbow, may be circling, too.

Boras is also an advocate for his players. And he’s got three core players all tied to the Rangers for at least five more years: Marcus Semien and Corey Seager signed willingly on; Josh Jung was drafted into it.

“I have great respect for ownership that has built this great foundation, but part and parcel of the commitment was to win multiple championships,” Boras said. “That core is built. It’s a club with championship calibrations. But there is still a need for pitching. When there is a player out there who is proven and can change the course of championship season, that is rare this time of year. It’s a clear bridge to the legacy both players and owners set out to achieve when their relationship began.”

Semien agreed: “When [Montgomery] joined the team, he fit right in and the pieces all came together and lined up. When you give up real pieces for that kind of player and it works out, you hope that player would come back. All you can do is pay attention to the best players that are out there. The best teams keep getting better.”

The Rangers finished 2023 as the best team.

They may still need to get better.

Boras would never tell them what to do. Only point out what others facing the same situation have done.

X: @Evan_P_Grant

Find more Rangers coverage from The Dallas Morning News here .

Click or tap here to sign up for our Rangers newsletter.

Evan Grant , Rangers beat writer/insider . Evan has covered the Rangers since 1997. He has twice been named one of the top 10 beat writers in the country by the AP Sports Editors. His passions outside of covering baseball are his wife, Gina, his two step kids, two crazy dogs & barbecue. Let's not discuss the cat. Evan graduated from Georgia State University, but oddly is a Georgia fan.

Top Sports Stories

Dallas mavericks’ win over a short-handed warriors highlighted by their paint dominance, dylan cease trade to padres leaves texas rangers with limited rotation options remaining, waiting for cowboys’ big free agency splash don’t be surprised by a few more ripples, mavericks’ luka doncic (hamstring) exits early vs. warriors, ending triple-double streak, texas basketball goes quietly vs. k-state in final big 12 conference tournament appearance.