type 1 error research

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base
• Type I & Type II Errors | Differences, Examples, Visualizations

Type I & Type II Errors | Differences, Examples, Visualizations

Published on January 18, 2021 by Pritha Bhandari . Revised on June 22, 2023.

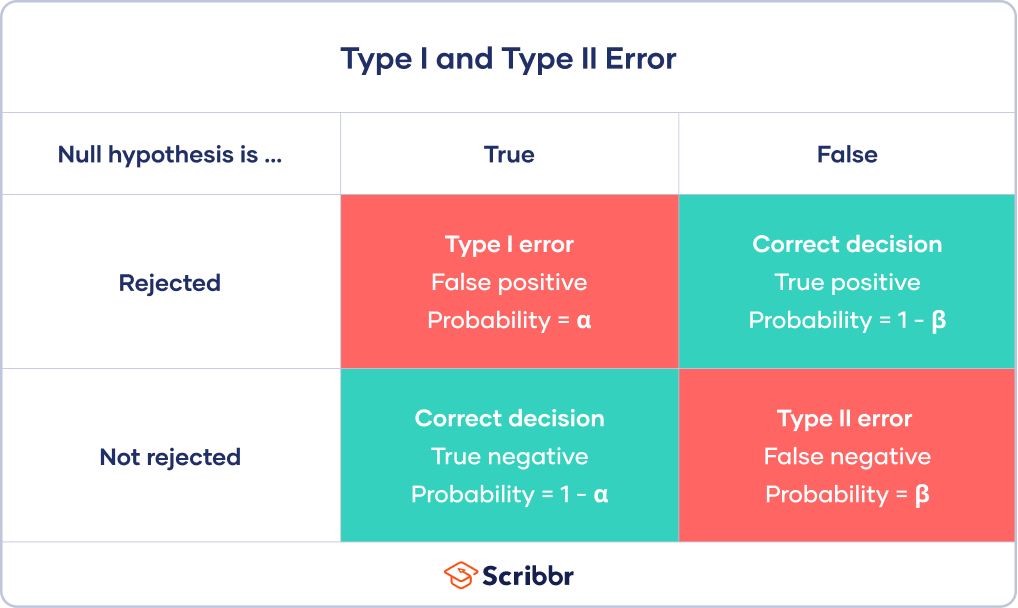
In statistics , a Type I error is a false positive conclusion, while a Type II error is a false negative conclusion.

Making a statistical decision always involves uncertainties, so the risks of making these errors are unavoidable in hypothesis testing .

The probability of making a Type I error is the significance level , or alpha (α), while the probability of making a Type II error is beta (β). These risks can be minimized through careful planning in your study design.

• Type I error (false positive) : the test result says you have coronavirus, but you actually don’t.
• Type II error (false negative) : the test result says you don’t have coronavirus, but you actually do.

Table of contents

Error in statistical decision-making, type i error, type ii error, trade-off between type i and type ii errors, is a type i or type ii error worse, other interesting articles, frequently asked questions about type i and ii errors.

Using hypothesis testing, you can make decisions about whether your data support or refute your research predictions with null and alternative hypotheses .

Hypothesis testing starts with the assumption of no difference between groups or no relationship between variables in the population—this is the null hypothesis . It’s always paired with an alternative hypothesis , which is your research prediction of an actual difference between groups or a true relationship between variables .

In this case:

• The null hypothesis (H 0 ) is that the new drug has no effect on symptoms of the disease.
• The alternative hypothesis (H 1 ) is that the drug is effective for alleviating symptoms of the disease.

Then , you decide whether the null hypothesis can be rejected based on your data and the results of a statistical test . Since these decisions are based on probabilities, there is always a risk of making the wrong conclusion.

• If your results show statistical significance , that means they are very unlikely to occur if the null hypothesis is true. In this case, you would reject your null hypothesis. But sometimes, this may actually be a Type I error.
• If your findings do not show statistical significance, they have a high chance of occurring if the null hypothesis is true. Therefore, you fail to reject your null hypothesis. But sometimes, this may be a Type II error.

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

• Academic style
• Vague sentences
• Style consistency

See an example

A Type I error means rejecting the null hypothesis when it’s actually true. It means concluding that results are statistically significant when, in reality, they came about purely by chance or because of unrelated factors.

The risk of committing this error is the significance level (alpha or α) you choose. That’s a value that you set at the beginning of your study to assess the statistical probability of obtaining your results ( p value).

The significance level is usually set at 0.05 or 5%. This means that your results only have a 5% chance of occurring, or less, if the null hypothesis is actually true.

If the p value of your test is lower than the significance level, it means your results are statistically significant and consistent with the alternative hypothesis. If your p value is higher than the significance level, then your results are considered statistically non-significant.

To reduce the Type I error probability, you can simply set a lower significance level.

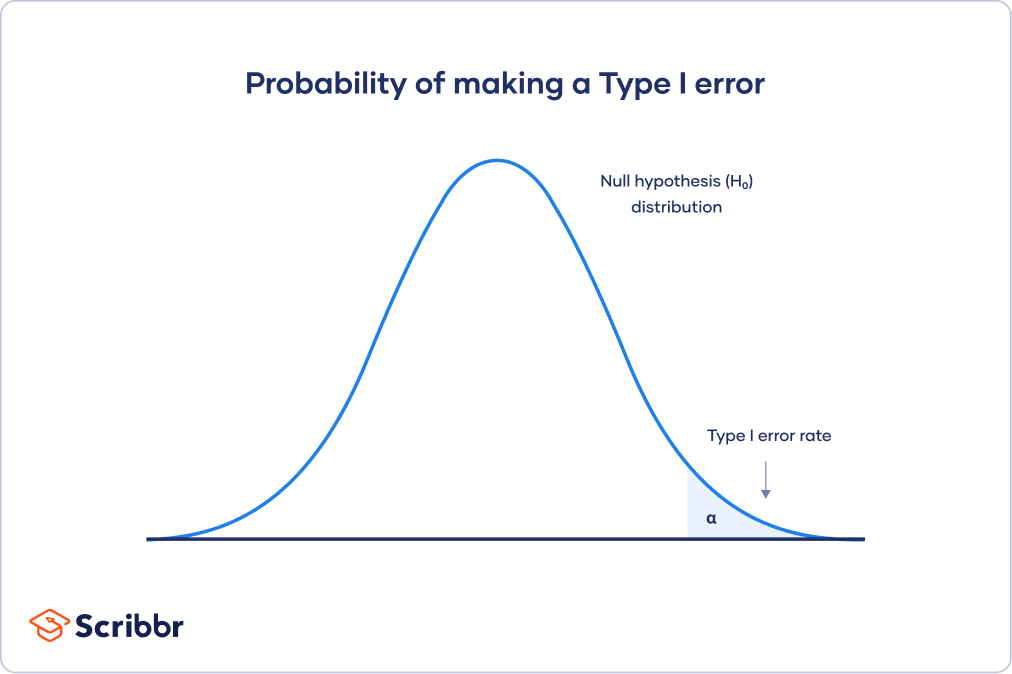
Type I error rate

The null hypothesis distribution curve below shows the probabilities of obtaining all possible results if the study were repeated with new samples and the null hypothesis were true in the population .

At the tail end, the shaded area represents alpha. It’s also called a critical region in statistics.

If your results fall in the critical region of this curve, they are considered statistically significant and the null hypothesis is rejected. However, this is a false positive conclusion, because the null hypothesis is actually true in this case!

A Type II error means not rejecting the null hypothesis when it’s actually false. This is not quite the same as “accepting” the null hypothesis, because hypothesis testing can only tell you whether to reject the null hypothesis.

Instead, a Type II error means failing to conclude there was an effect when there actually was. In reality, your study may not have had enough statistical power to detect an effect of a certain size.

Power is the extent to which a test can correctly detect a real effect when there is one. A power level of 80% or higher is usually considered acceptable.

The risk of a Type II error is inversely related to the statistical power of a study. The higher the statistical power, the lower the probability of making a Type II error.

Statistical power is determined by:

• Size of the effect : Larger effects are more easily detected.
• Measurement error : Systematic and random errors in recorded data reduce power.
• Sample size : Larger samples reduce sampling error and increase power.
• Significance level : Increasing the significance level increases power.

To (indirectly) reduce the risk of a Type II error, you can increase the sample size or the significance level.

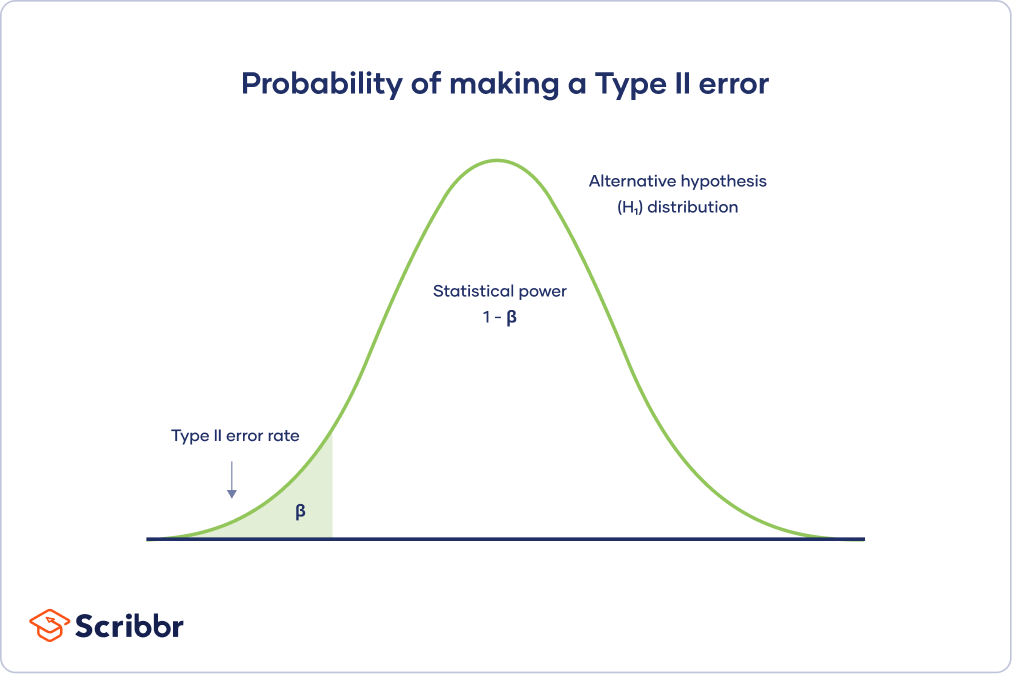
Type II error rate

The alternative hypothesis distribution curve below shows the probabilities of obtaining all possible results if the study were repeated with new samples and the alternative hypothesis were true in the population .

The Type II error rate is beta (β), represented by the shaded area on the left side. The remaining area under the curve represents statistical power, which is 1 – β.

Increasing the statistical power of your test directly decreases the risk of making a Type II error.

The Type I and Type II error rates influence each other. That’s because the significance level (the Type I error rate) affects statistical power, which is inversely related to the Type II error rate.

This means there’s an important tradeoff between Type I and Type II errors:

• Setting a lower significance level decreases a Type I error risk, but increases a Type II error risk.
• Increasing the power of a test decreases a Type II error risk, but increases a Type I error risk.

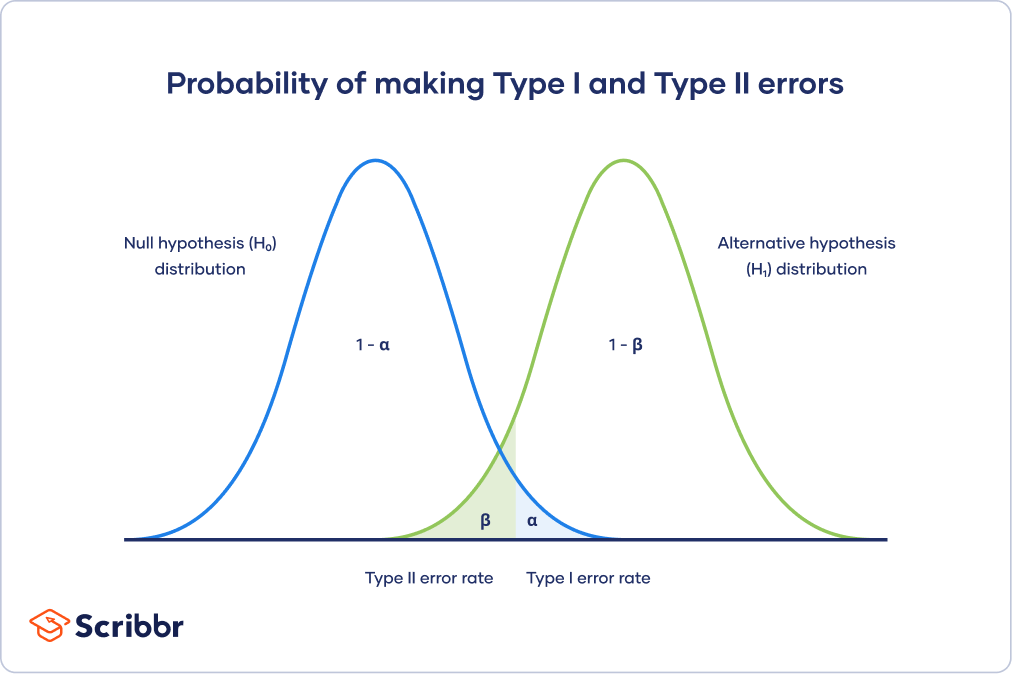
This trade-off is visualized in the graph below. It shows two curves:

• The null hypothesis distribution shows all possible results you’d obtain if the null hypothesis is true. The correct conclusion for any point on this distribution means not rejecting the null hypothesis.
• The alternative hypothesis distribution shows all possible results you’d obtain if the alternative hypothesis is true. The correct conclusion for any point on this distribution means rejecting the null hypothesis.

Type I and Type II errors occur where these two distributions overlap. The blue shaded area represents alpha, the Type I error rate, and the green shaded area represents beta, the Type II error rate.

By setting the Type I error rate, you indirectly influence the size of the Type II error rate as well.

It’s important to strike a balance between the risks of making Type I and Type II errors. Reducing the alpha always comes at the cost of increasing beta, and vice versa .

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

For statisticians, a Type I error is usually worse. In practical terms, however, either type of error could be worse depending on your research context.

A Type I error means mistakenly going against the main statistical assumption of a null hypothesis. This may lead to new policies, practices or treatments that are inadequate or a waste of resources.

In contrast, a Type II error means failing to reject a null hypothesis. It may only result in missed opportunities to innovate, but these can also have important practical consequences.

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Normal distribution
• Descriptive statistics
• Measures of central tendency
• Correlation coefficient
• Null hypothesis

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

In statistics, a Type I error means rejecting the null hypothesis when it’s actually true, while a Type II error means failing to reject the null hypothesis when it’s actually false.

The risk of making a Type I error is the significance level (or alpha) that you choose. That’s a value that you set at the beginning of your study to assess the statistical probability of obtaining your results ( p value ).

To reduce the Type I error probability, you can set a lower significance level.

The risk of making a Type II error is inversely related to the statistical power of a test. Power is the extent to which a test can correctly detect a real effect when there is one.

To (indirectly) reduce the risk of a Type II error, you can increase the sample size or the significance level to increase statistical power.

Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test . Significance is usually denoted by a p -value , or probability value.

Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis .

When the p -value falls below the chosen alpha value, then we say the result of the test is statistically significant.

In statistics, power refers to the likelihood of a hypothesis test detecting a true effect if there is one. A statistically powerful test is more likely to reject a false negative (a Type II error).

If you don’t ensure enough power in your study, you may not be able to detect a statistically significant result even when it has practical significance. Your study might not have the ability to answer your research question.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bhandari, P. (2023, June 22). Type I & Type II Errors | Differences, Examples, Visualizations. Scribbr. Retrieved March 25, 2024, from https://www.scribbr.com/statistics/type-i-and-type-ii-errors/

Is this article helpful?

Pritha Bhandari

Other students also liked, an easy introduction to statistical significance (with examples), understanding p values | definition and examples, statistical power and why it matters | a simple introduction, what is your plagiarism score.

Type 1 and Type 2 Errors in Statistics

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

On This Page:

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty). Because a p -value is based on probabilities, there is always a chance of making an incorrect conclusion regarding accepting or rejecting the null hypothesis ( H 0 ).

Anytime we make a decision using statistics, there are four possible outcomes, with two representing correct decisions and two representing errors.

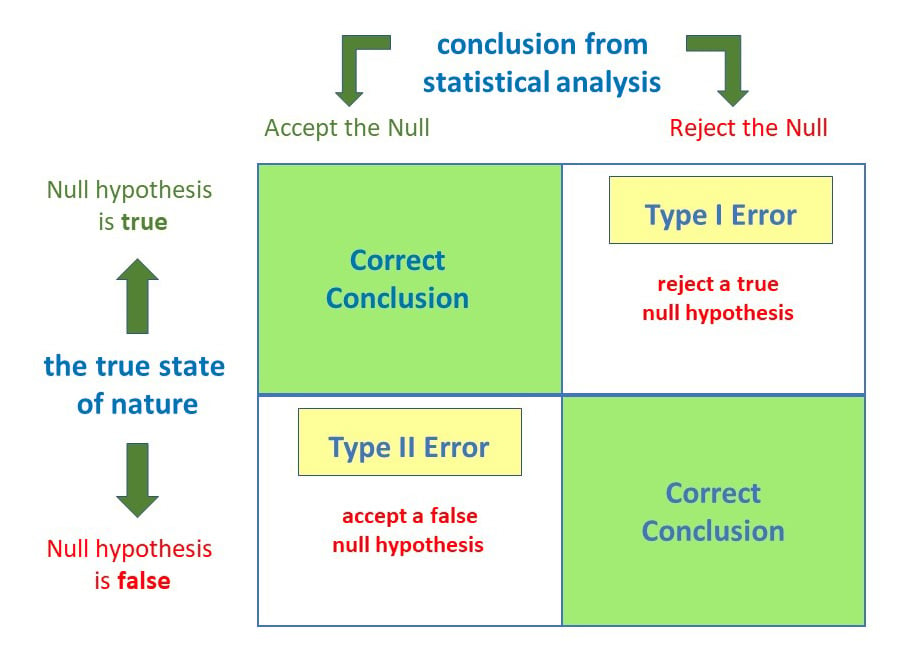
The chances of committing these two types of errors are inversely proportional: that is, decreasing type I error rate increases type II error rate and vice versa.

As the significance level (α) increases, it becomes easier to reject the null hypothesis, decreasing the chance of missing a real effect (Type II error, β). If the significance level (α) goes down, it becomes harder to reject the null hypothesis , increasing the chance of missing an effect while reducing the risk of falsely finding one (Type I error).

Type I error 

A type 1 error is also known as a false positive and occurs when a researcher incorrectly rejects a true null hypothesis. Simply put, it’s a false alarm.

This means that you report that your findings are significant when they have occurred by chance.

The probability of making a type 1 error is represented by your alpha level (α), the p- value below which you reject the null hypothesis.

A p -value of 0.05 indicates that you are willing to accept a 5% chance of getting the observed data (or something more extreme) when the null hypothesis is true.

You can reduce your risk of committing a type 1 error by setting a lower alpha level (like α = 0.01). For example, a p-value of 0.01 would mean there is a 1% chance of committing a Type I error.

However, using a lower value for alpha means that you will be less likely to detect a true difference if one really exists (thus risking a type II error).

Scenario: Drug Efficacy Study

Imagine a pharmaceutical company is testing a new drug, named “MediCure”, to determine if it’s more effective than a placebo at reducing fever. They experimented with two groups: one receives MediCure, and the other received a placebo.

• Null Hypothesis (H0) : MediCure is no more effective at reducing fever than the placebo.
• Alternative Hypothesis (H1) : MediCure is more effective at reducing fever than the placebo.

After conducting the study and analyzing the results, the researchers found a p-value of 0.04.

If they use an alpha (α) level of 0.05, this p-value is considered statistically significant, leading them to reject the null hypothesis and conclude that MediCure is more effective than the placebo.

However, MediCure has no actual effect, and the observed difference was due to random variation or some other confounding factor. In this case, the researchers have incorrectly rejected a true null hypothesis.

Error : The researchers have made a Type 1 error by concluding that MediCure is more effective when it isn’t.

Implications

Resource Allocation : Making a Type I error can lead to wastage of resources. If a business believes a new strategy is effective when it’s not (based on a Type I error), they might allocate significant financial and human resources toward that ineffective strategy.

Unnecessary Interventions : In medical trials, a Type I error might lead to the belief that a new treatment is effective when it isn’t. As a result, patients might undergo unnecessary treatments, risking potential side effects without any benefit.

Reputation and Credibility : For researchers, making repeated Type I errors can harm their professional reputation. If they frequently claim groundbreaking results that are later refuted, their credibility in the scientific community might diminish.

Type II error

A type 2 error (or false negative) happens when you accept the null hypothesis when it should actually be rejected.

Here, a researcher concludes there is not a significant effect when actually there really is.

The probability of making a type II error is called Beta (β), which is related to the power of the statistical test (power = 1- β). You can decrease your risk of committing a type II error by ensuring your test has enough power.

You can do this by ensuring your sample size is large enough to detect a practical difference when one truly exists.

Scenario: Efficacy of a New Teaching Method

Educational psychologists are investigating the potential benefits of a new interactive teaching method, named “EduInteract”, which utilizes virtual reality (VR) technology to teach history to middle school students.

They hypothesize that this method will lead to better retention and understanding compared to the traditional textbook-based approach.

• Null Hypothesis (H0) : The EduInteract VR teaching method does not result in significantly better retention and understanding of history content than the traditional textbook method.
• Alternative Hypothesis (H1) : The EduInteract VR teaching method results in significantly better retention and understanding of history content than the traditional textbook method.

The researchers designed an experiment where one group of students learns a history module using the EduInteract VR method, while a control group learns the same module using a traditional textbook.

After a week, the student’s retention and understanding are tested using a standardized assessment.

Upon analyzing the results, the psychologists found a p-value of 0.06. Using an alpha (α) level of 0.05, this p-value isn’t statistically significant.

Therefore, they fail to reject the null hypothesis and conclude that the EduInteract VR method isn’t more effective than the traditional textbook approach.

However, let’s assume that in the real world, the EduInteract VR truly enhances retention and understanding, but the study failed to detect this benefit due to reasons like small sample size, variability in students’ prior knowledge, or perhaps the assessment wasn’t sensitive enough to detect the nuances of VR-based learning.

Error : By concluding that the EduInteract VR method isn’t more effective than the traditional method when it is, the researchers have made a Type 2 error.

This could prevent schools from adopting a potentially superior teaching method that might benefit students’ learning experiences.

Missed Opportunities : A Type II error can lead to missed opportunities for improvement or innovation. For example, in education, if a more effective teaching method is overlooked because of a Type II error, students might miss out on a better learning experience.

Potential Risks : In healthcare, a Type II error might mean overlooking a harmful side effect of a medication because the research didn’t detect its harmful impacts. As a result, patients might continue using a harmful treatment.

Stagnation : In the business world, making a Type II error can result in continued investment in outdated or less efficient methods. This can lead to stagnation and the inability to compete effectively in the marketplace.

How do Type I and Type II errors relate to psychological research and experiments?

Type I errors are like false alarms, while Type II errors are like missed opportunities. Both errors can impact the validity and reliability of psychological findings, so researchers strive to minimize them to draw accurate conclusions from their studies.

How does sample size influence the likelihood of Type I and Type II errors in psychological research?

Sample size in psychological research influences the likelihood of Type I and Type II errors. A larger sample size reduces the chances of Type I errors, which means researchers are less likely to mistakenly find a significant effect when there isn’t one.

A larger sample size also increases the chances of detecting true effects, reducing the likelihood of Type II errors.

Are there any ethical implications associated with Type I and Type II errors in psychological research?

Yes, there are ethical implications associated with Type I and Type II errors in psychological research.

Type I errors may lead to false positive findings, resulting in misleading conclusions and potentially wasting resources on ineffective interventions. This can harm individuals who are falsely diagnosed or receive unnecessary treatments.

Type II errors, on the other hand, may result in missed opportunities to identify important effects or relationships, leading to a lack of appropriate interventions or support. This can also have negative consequences for individuals who genuinely require assistance.

Therefore, minimizing these errors is crucial for ethical research and ensuring the well-being of participants.

Further Information

• Publication manual of the American Psychological Association
• Statistics for Psychology Book Download

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Type I & Type II Errors | Differences, Examples, Visualizations

Type I & Type II Errors | Differences, Examples, Visualizations

Published on 18 January 2021 by Pritha Bhandari . Revised on 2 February 2023.

In statistics , a Type I error is a false positive conclusion, while a Type II error is a false negative conclusion.

Making a statistical decision always involves uncertainties, so the risks of making these errors are unavoidable in hypothesis testing .

The probability of making a Type I error is the significance level , or alpha (α), while the probability of making a Type II error is beta (β). These risks can be minimized through careful planning in your study design.

• Type I error (false positive) : the test result says you have coronavirus, but you actually don’t.
• Type II error (false negative) : the test result says you don’t have coronavirus, but you actually do.

Table of contents

Error in statistical decision-making, type i error, type ii error, trade-off between type i and type ii errors, is a type i or type ii error worse, frequently asked questions about type i and ii errors.

Using hypothesis testing, you can make decisions about whether your data support or refute your research predictions with null and alternative hypotheses .

Hypothesis testing starts with the assumption of no difference between groups or no relationship between variables in the population—this is the null hypothesis . It’s always paired with an alternative hypothesis , which is your research prediction of an actual difference between groups or a true relationship between variables .

In this case:

• The null hypothesis (H 0 ) is that the new drug has no effect on symptoms of the disease.
• The alternative hypothesis (H 1 ) is that the drug is effective for alleviating symptoms of the disease.

Then , you decide whether the null hypothesis can be rejected based on your data and the results of a statistical test . Since these decisions are based on probabilities, there is always a risk of making the wrong conclusion.

• If your results show statistical significance , that means they are very unlikely to occur if the null hypothesis is true. In this case, you would reject your null hypothesis. But sometimes, this may actually be a Type I error.
• If your findings do not show statistical significance, they have a high chance of occurring if the null hypothesis is true. Therefore, you fail to reject your null hypothesis. But sometimes, this may be a Type II error.

A Type I error means rejecting the null hypothesis when it’s actually true. It means concluding that results are statistically significant when, in reality, they came about purely by chance or because of unrelated factors.

The risk of committing this error is the significance level (alpha or α) you choose. That’s a value that you set at the beginning of your study to assess the statistical probability of obtaining your results ( p value).

The significance level is usually set at 0.05 or 5%. This means that your results only have a 5% chance of occurring, or less, if the null hypothesis is actually true.

If the p value of your test is lower than the significance level, it means your results are statistically significant and consistent with the alternative hypothesis. If your p value is higher than the significance level, then your results are considered statistically non-significant.

To reduce the Type I error probability, you can simply set a lower significance level.

Type I error rate

The null hypothesis distribution curve below shows the probabilities of obtaining all possible results if the study were repeated with new samples and the null hypothesis were true in the population .

At the tail end, the shaded area represents alpha. It’s also called a critical region in statistics.

If your results fall in the critical region of this curve, they are considered statistically significant and the null hypothesis is rejected. However, this is a false positive conclusion, because the null hypothesis is actually true in this case!

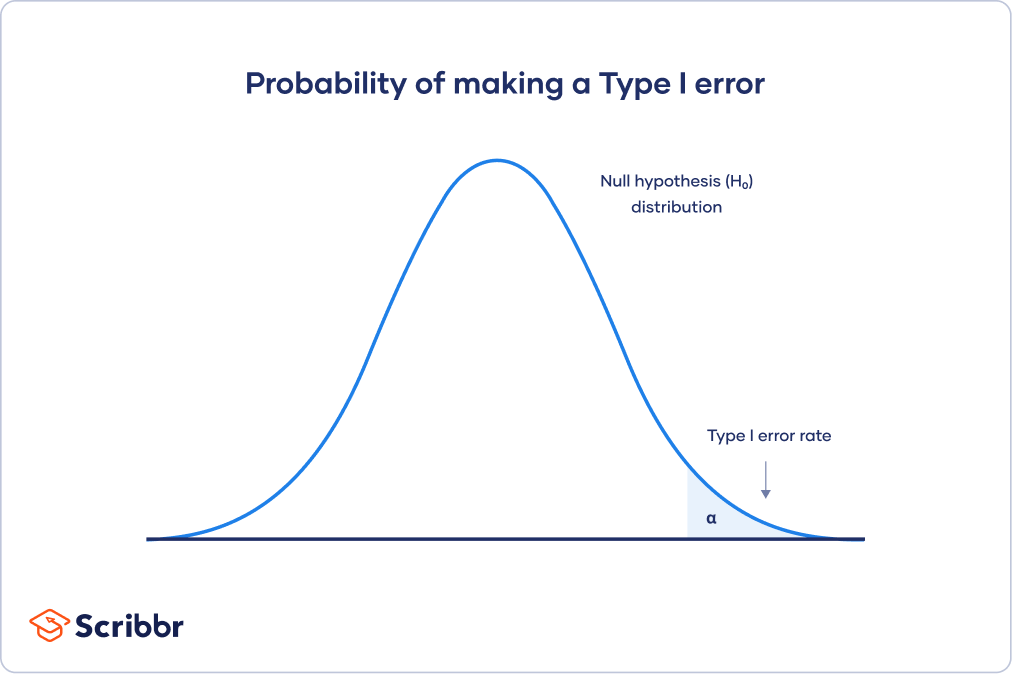
A Type II error means not rejecting the null hypothesis when it’s actually false. This is not quite the same as “accepting” the null hypothesis, because hypothesis testing can only tell you whether to reject the null hypothesis.

Instead, a Type II error means failing to conclude there was an effect when there actually was. In reality, your study may not have had enough statistical power to detect an effect of a certain size.

Power is the extent to which a test can correctly detect a real effect when there is one. A power level of 80% or higher is usually considered acceptable.

The risk of a Type II error is inversely related to the statistical power of a study. The higher the statistical power, the lower the probability of making a Type II error.

Statistical power is determined by:

• Size of the effect : Larger effects are more easily detected.
• Measurement error : Systematic and random errors in recorded data reduce power.
• Sample size : Larger samples reduce sampling error and increase power.
• Significance level : Increasing the significance level increases power.

To (indirectly) reduce the risk of a Type II error, you can increase the sample size or the significance level.

Type II error rate

The alternative hypothesis distribution curve below shows the probabilities of obtaining all possible results if the study were repeated with new samples and the alternative hypothesis were true in the population .

The Type II error rate is beta (β), represented by the shaded area on the left side. The remaining area under the curve represents statistical power, which is 1 – β.

Increasing the statistical power of your test directly decreases the risk of making a Type II error.

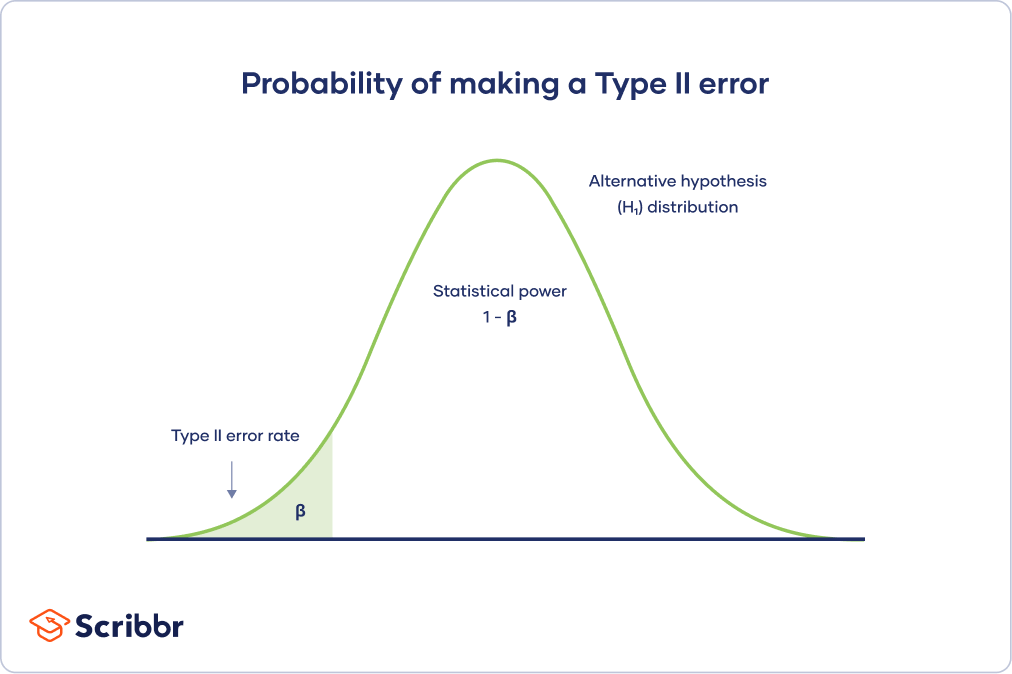
The Type I and Type II error rates influence each other. That’s because the significance level (the Type I error rate) affects statistical power, which is inversely related to the Type II error rate.

This means there’s an important tradeoff between Type I and Type II errors:

• Setting a lower significance level decreases a Type I error risk, but increases a Type II error risk.
• Increasing the power of a test decreases a Type II error risk, but increases a Type I error risk.

This trade-off is visualized in the graph below. It shows two curves:

• The null hypothesis distribution shows all possible results you’d obtain if the null hypothesis is true. The correct conclusion for any point on this distribution means not rejecting the null hypothesis.
• The alternative hypothesis distribution shows all possible results you’d obtain if the alternative hypothesis is true. The correct conclusion for any point on this distribution means rejecting the null hypothesis.

Type I and Type II errors occur where these two distributions overlap. The blue shaded area represents alpha, the Type I error rate, and the green shaded area represents beta, the Type II error rate.

By setting the Type I error rate, you indirectly influence the size of the Type II error rate as well.

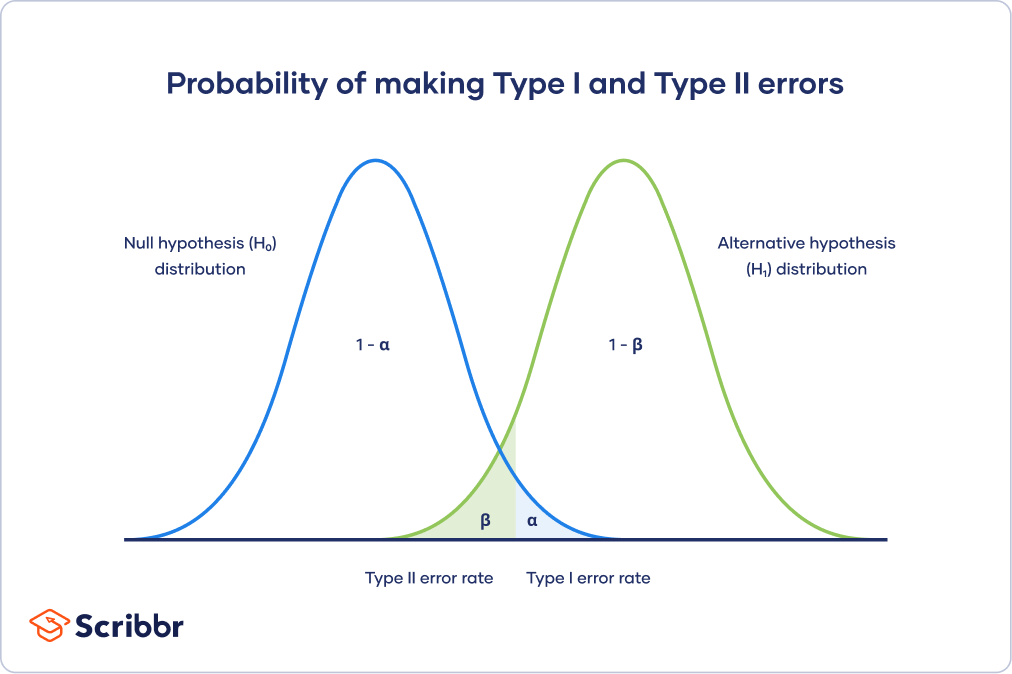
It’s important to strike a balance between the risks of making Type I and Type II errors. Reducing the alpha always comes at the cost of increasing beta, and vice versa .

For statisticians, a Type I error is usually worse. In practical terms, however, either type of error could be worse depending on your research context.

A Type I error means mistakenly going against the main statistical assumption of a null hypothesis. This may lead to new policies, practices or treatments that are inadequate or a waste of resources.

In contrast, a Type II error means failing to reject a null hypothesis. It may only result in missed opportunities to innovate, but these can also have important practical consequences.

In statistics, a Type I error means rejecting the null hypothesis when it’s actually true, while a Type II error means failing to reject the null hypothesis when it’s actually false.

The risk of making a Type I error is the significance level (or alpha) that you choose. That’s a value that you set at the beginning of your study to assess the statistical probability of obtaining your results ( p value ).

To reduce the Type I error probability, you can set a lower significance level.

The risk of making a Type II error is inversely related to the statistical power of a test. Power is the extent to which a test can correctly detect a real effect when there is one.

To (indirectly) reduce the risk of a Type II error, you can increase the sample size or the significance level to increase statistical power.

Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test . Significance is usually denoted by a p -value , or probability value.

Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis .

When the p -value falls below the chosen alpha value, then we say the result of the test is statistically significant.

In statistics, power refers to the likelihood of a hypothesis test detecting a true effect if there is one. A statistically powerful test is more likely to reject a false negative (a Type II error).

If you don’t ensure enough power in your study, you may not be able to detect a statistically significant result even when it has practical significance. Your study might not have the ability to answer your research question.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Bhandari, P. (2023, February 02). Type I & Type II Errors | Differences, Examples, Visualizations. Scribbr. Retrieved 25 March 2024, from https://www.scribbr.co.uk/stats/type-i-and-type-ii-error/

Is this article helpful?

Pritha Bhandari

• Search Search Please fill out this field.

What Is a Type I Error?

• How It Works
• False Positive

The Bottom Line

• Business Leaders
• Math and Statistics

Type 1 Error: Definition, False Positives, and Examples

ljubaphoto / Getty Images

In statistical research, a type 1 error is when the null hypothesis is rejected, which incorrectly leads to the study stating that notable differences were found in the variables when actually there were no differences. Put simply, a type I error is a false positive result.

Making a type I error often can't be avoided because of the degree of uncertainty involved. A null hypothesis is established during hypothesis testing before a test begins. In some cases, a type I error assumes there's no cause-and-effect relationship between the tested item and the stimuli to trigger an outcome to the test.

Key Takeaways

• A type I error occurs during hypothesis testing when a null hypothesis is rejected, even though it is accurate and should not be rejected.
• Hypothesis testing is a testing process that uses sample data.
• The null hypothesis assumes no cause-and-effect relationship between the tested item and the stimuli applied during the test.
• A type I error is a false positive leading to an incorrect rejection of the null hypothesis.
• A false positive can occur if something other than the stimuli causes the outcome of the test.

How a Type I Error Works

Hypothesis testing is a testing process that uses sample data. The test is designed to provide evidence that the hypothesis or conjecture is supported by the data being tested. A null hypothesis is a belief that there is no statistical significance or effect between the two data sets, variables, or populations being considered in the hypothesis. A researcher would generally try to disprove the null hypothesis.

For example, let's say the null hypothesis states that an investment strategy doesn't perform any better than a market index like the S&P 500 . The researcher would take samples of data and test the historical performance of the investment strategy to determine if the strategy performed at a higher level than the S&P. If the test results show that the strategy performed at a higher rate than the index, the null hypothesis is rejected.

This condition is denoted as n=0. If the result seems to indicate that the stimuli applied to the test subject caused a reaction when the test is conducted, the null hypothesis stating that the stimuli do not affect the test subject then needs to be rejected.

A null hypothesis should ideally never be rejected if it's found to be true. It should always be rejected if it's found to be false. However, there are situations when errors can occur.

False Positive Type I Error

A type I error is also called a false positive result. This result leads to an incorrect rejection of the null hypothesis. It rejects an idea that shouldn't have been rejected in the first place.

Rejecting the null hypothesis under the assumption that there is no relationship between the test subject, the stimuli, and the outcome may sometimes be incorrect. If something other than the stimuli causes the outcome of the test, it can cause a false positive result.

Examples of Type I Errors

Let's look at a couple of hypothetical examples to show how type I errors occur.

Criminal Trials

Type I errors commonly occur in criminal trials, where juries are required to come up with a verdict of either innocent or guilty. In this case, the null hypothesis is that the person is innocent, while the alternative is guilty. A jury may come up with a type I error if the members find that the person is found guilty and is sent to jail, despite actually being innocent.

Medical Testing

In medical testing, a type I error would cause the appearance that a treatment for a disease has the effect of reducing the severity of the disease when, in fact, it does not. When a new medicine is being tested, the null hypothesis will be that the medicine does not affect the progression of the disease.

Let's say a lab is researching a new cancer drug . Their null hypothesis might be that the drug does not affect the growth rate of cancer cells.

After applying the drug to the cancer cells, the cancer cells stop growing. This would cause the researchers to reject their null hypothesis that the drug would have no effect. If the drug caused the growth stoppage, the conclusion to reject the null, in this case, would be correct.

However, if something else during the test caused the growth stoppage instead of the administered drug, this would be an example of an incorrect rejection of the null hypothesis (i.e., a type I error).

How Does a Type I Error Occur?

A type I error occurs when the null hypothesis, which is the belief that there is no statistical significance or effect between the data sets considered in the hypothesis, is mistakenly rejected. The type I error should never be rejected even though it's accurate. It is also known as a false positive result.

What Is the Difference Between a Type I and Type II Error?

Type I and type II errors occur during statistical hypothesis testing. While the type I error (a false positive) rejects a null hypothesis when it is, in fact, correct, the type II error (a false negative) fails to reject a false null hypothesis. For example, a type I error would convict someone of a crime when they are actually innocent. A type II error would acquit a guilty individual when they are guilty of a crime.

What Is a Null Hypothesis?

A null hypothesis occurs in statistical hypothesis testing. It states that no relationship exists between two data sets or populations. When a null hypothesis is accurate and rejected, the result is a false positive or a type I error. When it is false and fails to be rejected, a false negative occurs. This is also referred to as a type II error.

What's the Difference Between a Type I Error and a False Positive?

A type I error is often called a false positive. This occurs when the null hypothesis is rejected even though it's correct. The rejection takes place because of the assumption that there is no relationship between the data sets and the stimuli. As such, the outcome is assumed to be incorrect.

Hypothesis testing is a form of testing that uses data sets to either accept or determine a specific outcome using a null hypothesis. Although we often don't realize it, we use hypothesis testing in our everyday lives.

This comes in many areas, such as making investment decisions or deciding the fate of a person in a criminal trial. Sometimes, the result may be a type I error. This false positive is the incorrect rejection of the null hypothesis even when it is true.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.2: Type I and II Errors

• Last updated
• Save as PDF
• Page ID 24056

• Rachel Webb
• Portland State University

How do you quantify really small? Is 5% or 10% or 15% really small? How do you decide? That depends on your field of study and the importance of the situation. Is this a pilot study? Is someone’s life at risk? Would you lose your job? Most industry standards use 5% as the cutoff point for how small is small enough, but 1%, 5% and 10% are frequently used depending on what the situation calls for.

Now, how small is small enough? To answer that, you really want to know the types of errors you can make in hypothesis testing.

The first error is if you say that H 0 is false, when in fact it is true. This means you reject H 0 when H 0 was true. The second error is if you say that H 0 is true, when in fact it is false. This means you fail to reject H 0 when H 0 is false.

Figure 8-4 shows that if we “Reject H 0 ” when H 0 is actually true, we are committing a type I error. The probability of committing a type I error is the Greek letter \(\alpha\), pronounced alpha. This can be controlled by the researcher by choosing a specific level of significance \(\alpha\).

Figure 8-4 shows that if we “Do Not Reject H 0 ” when H 0 is actually false, we are committing a type II error. The probability of committing a type II error is denoted with the Greek letter β, pronounced beta. When we increase the sample size this will reduce β. The power of a test is 1 – β.

A jury trial is about to take place to decide if a person is guilty of committing murder. The hypotheses for this situation would be:

• \(H_0\): The defendant is innocent
• \(H_1\): The defendant is not innocent

The jury has two possible decisions to make, either acquit or convict the person on trial, based on the evidence that is presented. There are two possible ways that the jury could make a mistake. They could convict an innocent person or they could let a guilty person go free. Both are bad news, but if the death penalty was sentenced to the convicted person, the justice system could be killing an innocent person. If a murderer is let go without enough evidence to convict them then they could possibly murder again. In statistics we call these two types of mistakes a type I and II error.

Figure 8-5 is a diagram to see the four possible jury decisions and two errors.

Type I Error is rejecting H 0 when H 0 is true, and Type II Error is failing to reject H 0 when H 0 is false.

Since these are the only two possible errors, one can define the probabilities attached to each error.

\(\alpha\) = P(Type I Error) = P(Rejecting H 0 | H 0 is true)

β = P(Type II Error) = P(Failing to reject H 0 | H 0 is false)

An investment company wants to build a new food cart. They know from experience that food carts are successful if they have on average more than 100 people a day walk by the location. They have a potential site to build on, but before they begin, they want to see if they have enough foot traffic. They observe how many people walk by the site every day over a month. They will build if there is more than an average of 100 people who walk by the site each day. In simple terms, explain what the type I & II errors would be using context from the problem.

The hypotheses are: H 0 : μ = 100 and H 1 : μ > 100.

Sometimes it is helpful to use words next to your hypotheses instead of the formal symbols

• H 0 : μ ≤ 100 (Do not build)
• H 1 : μ > 100 (Build).

A type I error would be to reject the null when in fact it is true. Take your finger and cover up the null hypothesis (our decision is to reject the null), then what is showing? The alternative hypothesis is what action we take.

If we reject H 0 then we would build the new food cart. However, H 0 was actually true, which means that the mean was less than or equal to 100 people walking by.

In more simple terms, this would mean that our evidence showed that we have enough foot traffic to support the food cart. Once we build, though, there was not on average more than 100 people that walk by and the food cart may fail.

A type II error would be to fail to reject the null when in fact the null is false. Evidence shows that we should not build on the site, but this actually would have been a prime location to build on.

The missed opportunity of a type II error is not as bad as possibly losing thousands of dollars on a bad investment.

What is more severe of an error is dependent on what side of the desk you are sitting on. For instance, if a hypothesis is about miles per gallon for a new car the hypotheses may be set up differently depending on if you are buying the car or selling the car. For this course, the claim will be stated in the problem and always set up the hypotheses to match the stated claim. In general, the research question should be set up as some type of change in the alternative hypothesis.

Controlling for Type I Error

The significance level used by the researcher should be picked prior to collection and analyzing data. This is called “a priori,” versus picking α after you have done your analysis which is called “post hoc.” When deciding on what significance level to pick, one needs to look at the severity of the consequences of the type I and type II errors. For example, if the type I error may cause the loss of life or large amounts of money the researcher would want to set \(\alpha\) low.

Controlling for Type II Error

The power of a test is the complement of a type II error or correctly rejecting a false null hypothesis. You can increase the power of the test and hence decrease the type II error by increasing the sample size. Similar to confidence intervals, where we can reduce our margin of error when we increase the sample size. In general, we would like to have a high confidence level and a high power for our hypothesis tests. When you increase your confidence level, then in turn the power of the test will decrease. Calculating the probability of a type II error is a little more difficult and it is a conditional probability based on the researcher’s hypotheses and is not discussed in this course.

“‘That's right!’ shouted Vroomfondel, ‘we demand rigidly defined areas of doubt and uncertainty!’” (Adams, 2002)

Visualizing \(\alpha\) and β

If \(\alpha\) increases that means the chances of making a type I error will increase. It is more likely that a type I error will occur. It makes sense that you are less likely to make type II errors, only because you will be rejecting H 0 more often. You will be failing to reject H 0 less, and therefore, the chance of making a type II error will decrease. Thus, as α increases, β will decrease, and vice versa. That makes them seem like complements, but they are not complements. Consider one more factor – sample size.

Consider if you have a larger sample that is representative of the population, then it makes sense that you have more accuracy than with a smaller sample. Think of it this way, which would you trust more, a sample mean of 890 if you had a sample size of 35 or sample size of 350 (assuming a representative sample)? Of course, the 350 because there are more data points and so more accuracy. If you are more accurate, then there is less chance that you will make any error.

By increasing the sample size of a representative sample, you decrease β.

• For a constant sample size, n , if \(\alpha\) increases, β decreases.
• For a constant significance level, \(\alpha\), if n increases, β decreases.

When the sample size becomes large, point estimates become more precise and any real differences in the mean and null value become easier to detect and recognize. Even a very small difference would likely be detected if we took a large enough sample size. Sometimes researchers will take such a large sample size that even the slightest difference is detected. While we still say that difference is statistically significant, it might not be practically significant. Statistically significant differences are sometimes so minor that they are not practically relevant. This is especially important to research: if we conduct a study, we want to focus on finding a meaningful result. We do not want to spend lots of money finding results that hold no practical value.

The role of a statistician in conducting a study often includes planning the size of the study. The statistician might first consult experts or scientific literature to learn what would be the smallest meaningful difference from the null value. They also would obtain some reasonable estimate for the standard deviation. With these important pieces of information, they would choose a sufficiently large sample size so that the power for the meaningful difference is perhaps 80% or 90%. While larger sample sizes may still be used, the statistician might advise against using them in some cases, especially in sensitive areas of research.

If we look at the following two sampling distributions in Figure 8-6, the one on the left represents the sampling distribution for the true unknown mean. The curve on the right represents the sampling distribution based on the hypotheses the researcher is making. Do you remember the difference between a sampling distribution, the distribution of a sample, and the distribution of the population? Revisit the Central Limit Theorem in Chapter 6 if needed.

If we start with \(\alpha\) = 0.05, the critical value is represented by the vertical green line at \(z_{\alpha}\) = 1.96. Then the blue shaded area to the right of this line represents \(\alpha\). The area under the curve to the left of \(z_{\alpha / 2}\) = 1.96 based on the researcher’s claim would represent β.

If we were to change \(\alpha\) from 0.05 to 0.01 then we get a critical value of \(z_{\alpha / 2}\) = 2.576. Note that when \(\alpha\) decreases, then β increases which means your power 1 – β decreases. See Figure 8-7.

This text does not go over how to calculate β. You will need to be able to write out a sentence interpreting either the type I or II errors given a set of hypotheses. You also need to know the relationship between \(\alpha\), β, confidence level, and power.

Hypothesis tests are not flawless, since we can make a wrong decision in statistical hypothesis tests based on the data. For example, in the court system, innocent people are sometimes wrongly convicted and the guilty sometimes walk free, or diagnostic tests that have false negatives or false positives. However, the difference is that in statistical hypothesis tests, we have the tools necessary to quantify how often we make such errors. A type I Error is rejecting the null hypothesis when H 0 is actually true. A type II Error is failing to reject the null hypothesis when the alternative is actually true (H 0 is false).

We use the symbols \(\alpha\) = P(Type I Error) and β = P(Type II Error). The critical value is a cutoff point on the horizontal axis of the sampling distribution that you can compare your test statistic to see if you should reject the null hypothesis. For a left-tailed test the critical value will always be on the left side of the sampling distribution, the right-tailed test will always be on the right side, and a two-tailed test will be on both tails. Use technology to find the critical values. Most of the time in this course the shortcut menus that we use will give you the critical values as part of the output.

8.2.1 Finding Critical Values

A researcher decides they want to have a 5% chance of making a type I error so they set α = 0.05. What z-score would represent that 5% area? It would depend on if the hypotheses were a left-tailed, two-tailed or right-tailed test. This zscore is called a critical value. Figure 8-8 shows examples of critical values for the three possible sets of hypotheses.

Two-tailed Test

If we are doing a two-tailed test then the \(\alpha\) = 5% area gets divided into both tails. We denote these critical values \(z_{\alpha / 2}\) and \(z_{1-\alpha / 2}\). When the sample data finds a z-score ( test statistic ) that is either less than or equal to \(z_{\alpha / 2}\) or greater than or equal to \(z_{1-\alpha / 2}\) then we would reject H 0 . The area to the left of the critical value \(z_{\alpha / 2}\) and to the right of the critical value \(z_{1-\alpha / 2}\) is called the critical or rejection region. See Figure 8-9.

When \(\alpha\) = 0.05 then the critical values \(z_{\alpha / 2}\) and \(z_{1-\alpha / 2}\) are found using the following technology.

Excel: \(z_{\alpha / 2}\) =NORM.S.INV(0.025) = –1.96 and \(z_{1-\alpha / 2}\) =NORM.S.INV(0.975) = 1.96

TI-Calculator: \(z_{\alpha / 2}\) = invNorm(0.025,0,1) = –1.96 and \(z_{1-\alpha / 2}\) = invNorm(0.975,0,1) = 1.96

Since the normal distribution is symmetric, you only need to find one side’s z-score and we usually represent the critical values as ± \(z_{\alpha / 2}\).

Most of the time we will be finding a probability (p-value) instead of the critical values. The p-value and critical values are related and tell the same information so it is important to know what a critical value represents.

Right-tailed Test

If we are doing a right-tailed test then the \(\alpha\) = 5% area goes into the right tail. We denote this critical value \(z_{1-\alpha}\). When the sample data finds a z-score more than \(z_{1-\alpha}\) then we would reject H 0 , reject H 0 if the test statistic is ≥ \(z_{1-\alpha}\). The area to the right of the critical value \(z_{1-\alpha}\) is called the critical region. See Figure 8-10.

Figure 8-10

When \(\alpha\) = 0.05 then the critical value \(z_{1-\alpha}\) is found using the following technology.

Excel: \(z_{1-\alpha}\) =NORM.S.INV(0.95) = 1.645 Figure 8-10

TI-Calculator: \(z_{1-\alpha}\) = invNorm(0.95,0,1) = 1.645

Left-tailed Test

If we are doing a left-tailed test then the \(\alpha\) = 5% area goes into the left tail. If the sampling distribution is a normal distribution then we can use the inverse normal function in Excel or calculator to find the corresponding z-score. We denote this critical value \(z_{\alpha}\).

When the sample data finds a z-score less than \(z_{\alpha}\) then we would reject H0, reject Ho if the test statistic is ≤ \(z_{\alpha}\). The area to the left of the critical value \(z_{\alpha}\) is called the critical region. See Figure 8-11.

Figure 8-11

When \(\alpha\) = 0.05 then the critical value \(z_{\alpha}\) is found using the following technology.

Excel: \(z_{\alpha}\) =NORM.S.INV(0.05) = –1.645

TI-Calculator: \(z_{\alpha}\) = invNorm(0.05,0,1) = –1.645

The Claim and Summary

The wording on the summary statement changes depending on which hypothesis the researcher claims to be true. We really should always be setting up the claim in the alternative hypothesis since most of the time we are collecting evidence to show that a change has occurred, but occasionally a textbook will have the claim in the null hypothesis. Do not use the phrase “accept H 0 ” since this implies that H0 is true. The lack of evidence is not evidence of nothing.

There were only two possible correct answers for the decision step.

i. Reject H 0

ii. Fail to reject H 0

Caution! If we fail to reject the null this does not mean that there was no change, we just do not have any evidence that change has occurred. The absence of evidence is not evidence of absence. On the other hand, we need to be careful when we reject the null hypothesis we have not proved that there is change.

When we reject the null hypothesis, there is only evidence that a change has occurred. Our evidence could have been false and lead to an incorrect decision. If we use the phrase, “accept H 0 ” this implies that H 0 was true, but we just do not have evidence that it is false. Hence you will be marked incorrect for your decision if you use accept H 0 , use instead “fail to reject H 0 ” or “do not reject H 0 .”

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6.1 - type i and type ii errors.

When conducting a hypothesis test there are two possible decisions: reject the null hypothesis or fail to reject the null hypothesis. You should remember though, hypothesis testing uses data from a sample to make an inference about a population. When conducting a hypothesis test we do not know the population parameters. In most cases, we don't know if our inference is correct or incorrect.

When we reject the null hypothesis there are two possibilities. There could really be a difference in the population, in which case we made a correct decision. Or, it is possible that there is not a difference in the population (i.e., \(H_0\) is true) but our sample was different from the hypothesized value due to random sampling variation. In that case we made an error. This is known as a Type I error.

When we fail to reject the null hypothesis there are also two possibilities. If the null hypothesis is really true, and there is not a difference in the population, then we made the correct decision. If there is a difference in the population, and we failed to reject it, then we made a Type II error.

Rejecting \(H_0\) when \(H_0\) is really true, denoted by \(\alpha\) ("alpha") and commonly set at .05

     \(\alpha=P(Type\;I\;error)\)

Failing to reject \(H_0\) when \(H_0\) is really false, denoted by \(\beta\) ("beta")

     \(\beta=P(Type\;II\;error)\)

Example: Trial Section  

A man goes to trial where he is being tried for the murder of his wife.

We can put it in a hypothesis testing framework. The hypotheses being tested are:

• \(H_0\) : Not Guilty
• \(H_a\) : Guilty

Type I error  is committed if we reject \(H_0\) when it is true. In other words, did not kill his wife but was found guilty and is punished for a crime he did not really commit.

Type II error  is committed if we fail to reject \(H_0\) when it is false. In other words, if the man did kill his wife but was found not guilty and was not punished.

Example: Culinary Arts Study Section  

A group of culinary arts students is comparing two methods for preparing asparagus: traditional steaming and a new frying method. They want to know if patrons of their school restaurant prefer their new frying method over the traditional steaming method. A sample of patrons are given asparagus prepared using each method and asked to select their preference. A statistical analysis is performed to determine if more than 50% of participants prefer the new frying method:

• \(H_{0}: p = .50\)
• \(H_{a}: p>.50\)

Type I error  occurs if they reject the null hypothesis and conclude that their new frying method is preferred when in reality is it not. This may occur if, by random sampling error, they happen to get a sample that prefers the new frying method more than the overall population does. If this does occur, the consequence is that the students will have an incorrect belief that their new method of frying asparagus is superior to the traditional method of steaming.

Type II error  occurs if they fail to reject the null hypothesis and conclude that their new method is not superior when in reality it is. If this does occur, the consequence is that the students will have an incorrect belief that their new method is not superior to the traditional method when in reality it is.

• Type I vs Type II Errors: Causes, Examples & Prevention

There are two common types of errors, type I and type II errors you’ll likely encounter when testing a statistical hypothesis. The mistaken rejection of the finding or the null hypothesis is known as a type I error. In other words, type I error is the false-positive finding in hypothesis testing . Type II error on the other hand is the false-negative finding in hypothesis testing.

To better understand the two types of errors, here’s an example:

Let’s assume you notice some flu-like symptoms and decide to go to a hospital to get tested for the presence of malaria. There is a possibility of two errors occurring:

• In type I error (False positive): The result of the test shows you have malaria but you actually don’t have it.
• Type II error (false negative): The test result indicates that you don’t have malaria when you in fact do.

Type I error and Type II error are extensively used in areas such as computer science, Engineering, Statistics, and many more.

The chance of committing a type I error is known as alpha (α), while the chance of committing a type II error is known as beta (β). If you carefully plan your study design, you can minimize the probability of committing either of the errors.

Read: Survey Errors To Avoid: Types, Sources, Examples, Mitigation

What are Type I Errors?

Type I error is an omission that happens when a null hypothesis is reprobated during hypothesis testing. This is when it is indeed precise or positive and should not have been initially disapproved. So if a null hypothesis is erroneously rejected when it is positive, it is called a Type I error.

What this means is that results are concluded to be significant when in actual fact, it was obtained by chance.

When conducting hypothesis testing, a null hypothesis is determined before carrying out the actual test. The null hypothesis may presume that there is no chain of circumstances between the items being tested which may cause an outcome for the test.

When a null hypothesis is rejected, it means a chain of circumstances has been established between the items being tested even though it is a false alarm or false positive. This could lead to an error or many errors in a test, known as a Type I error.

It is worthy of note that statistical outcomes of every testing involve uncertainties, so making errors while performing these hypothesis testings is unavoidable. It is inherent that type I error may be considered as an error of commission in the sense that the producer or researcher mistakenly decides on a false outcome.

Read: Systematic Errors in Research: Definition, Examples

Causes of Type I Error

• When a factor other than the variable affects the variables being tested. This factor that causes the effect produces a result that supports the decision to reject the null hypothesis.
• When the result of a hypothesis testing is caused by chance, it is a Type I error. 
• Lastly, because a null hypothesis and the significance level are decided before conducting a hypothesis test, and also the sample size is not considered, a type I error may occur due to chance.

Read: Margin of error – Definition, Formula + Application

Risk Factor and Probability of Type I Error

• The risk factor and probability of Type I error are mostly set in advance and the level of significance of the hypothesis testing is known.
• The level of significance in a test is represented by α and it signifies the rate of the possibility of Type I error.
• While it is possible to reduce the rate of Type I error by using a determined sample size. The consequence of this, however, is that the possibility of a Type II error occurring in a test will increase.
• In a case where Type I error is decided at 5 percent, it means in the null hypothesis ( H 0), chances are there that 5 in the 100 hypotheses even if true will be rejected.
• Another risk factor is that both Type I and Type II errors can not be changed simultaneously. To reduce the possibility of one error occurring means the possibility of the other error will increase. Hence changing the outcome of one test inherently affects the outcome of the other test.

Read: Sampling Bias: Definition, Types + [Examples]

Consequences of a Type I Error

A type I error will result in a false alarm. The outcome of the hypothesis testing will be a false positive. This implies that the researcher decided the result of a hypothesis testing is true when in fact, it is not. 

For a sales group, the consequences of a type I error may result in losing potential market and missing out on probable sales because the findings of a test are faulty.

What are Type II Errors?

A Type II error means a researcher or producer did not disapprove of the alternate hypothesis when it is in fact negative or false. This does not mean the null hypothesis is accepted as positive as hypothesis testing only indicates if a null hypothesis should be rejected.

A Type II error means a conclusion on the effect of the test wasn’t recognized when an effect truly existed. Before a test can be said to have a real effect, it has to have a power level that is 80% or more.

This implies the statistical power of a test determines the risk of a type II error. The probability of a type II error occurring largely depends on how high the statistical power is.

Note: Null hypothesis is represented as (H0) and alternative hypothesis is represented as (H1)

Causes of Type II Error

• Type II error is mainly caused by the statistical power of a test being low. A Type II error will occur if the statistical test is not powerful enough. 
• The size of the sample can also lead to a Type I error because the outcome of the test will be affected. A small sample size might hide the significant level of the items being tested.
• Another cause of Type Ii error is the possibility that a researcher may disapprove of the actual outcome of a hypothesis even when it is correct.

Probability of Type II Error

• To arrive at the possibility of a Type II error occurring, the power of the test must be deducted from type 1.
• The level of significance in a test is represented by β and it shows the rate of the possibility of Type I error. 
• It is possible to reduce the rate of Type II error if the significance level of the test is increased.
• In a case where Type II error is decided at 5 percent, it means in the null hypothesis ( H 0), chances are there that 5 in the 100 hypotheses even if it is false will be accepted.
•  Type I error and Type II error are connected. Hence, to reduce the possibility of one type of error from occurring means the possibility of the other error will increase.
• It is important to decide which error has lesser effects on the test.

Consequences of a Type II Error

Type II errors can also result in a wrong decision that will affect the outcomes of a test and have real-life consequences.  

Note that even if you proved your test hypothesis, your conversion result can invalidate the outcome unintended. This turn of events can be discouraging, hence the need to be extra careful when conducting hypothesis testing.  

How to Avoid Type I and II errors

Type I error and type II errors can not be entirely avoided in hypothesis testing, but the researcher can reduce the probability of them occurring.

For Type I error, minimize the significance level to avoid making errors. This can be determined by the researcher. 

To avoid type II errors, ensure the test has high statistical power. The higher the statistical power, the higher the chance of avoiding an error. Set your statistical power to 80% and above and conduct your test.

Increase the sample size of the hypothesis testing.

The Type II error can also be avoided if the significance level of the test hypothesis is chosen.

How to Detect Type I and Type II Errors in Data

After completing a study, the researcher can conduct any of the available statistical tests to reject the default hypothesis in favor of its alternative. If the study is free of bias, there are four possible outcomes. See the image below;

Image source: IPJ

If the findings in the sample and reality in the population match, the researchers’ inferences will be correct. However, if in any of the situations a type I or II error has been made, the inference will be incorrect. 

Key Differences between Type I & II Errors

• In statistical hypothesis testing, a type I error is caused by disapproving a null hypothesis that is otherwise correct while in contrast, Type II error occurs when the null hypothesis is not rejected even though it is not true.
• Type I error is the same as a false alarm or false positive while Type II error is also referred to as false negative.
• A Type I error is represented by α while a Type II error is represented by β.
• The level of significance determines the possibility of a type I error while type II error is the possibility of deducting the power of the test from 1.
• You can decrease the possibility of Type I error by reducing the level of significance. The same way you can reduce the probability of a Type II error by increasing the significance level of the test.
• Type I error occurs when you reject the null hypothesis, in contrast, Type II error occurs when you accept an incorrect outcome of a false hypothesis

Examples of Type I & II errors

Type i error examples.

To understand the statistical significance of Type I error, let us look at this example.

In this hypothesis, a driver wants to determine the relationship between him getting a new driving wheel and the number of passengers he carries in a week.

Now, if the number of passengers he carries in a week increases after he got a new driving wheel than the number of passengers he carried in a week with the old driving wheel, this driver might assume that there is a relationship between the new wheel and the increase in the number of passengers and support the alternative hypothesis.

However, the increment in the number of passengers he carried in a week, might have been influenced by chance and not by the new wheel which results in type I error.

By this indication, the driver should have supported the null hypothesis because the increment of his passengers might have been due to chance and not fact. 

Type II error examples

For Type II error and statistical power, let us assume a hypothesis where a farmer that rears birds assumes none of his birds have bird-flu. He observes his birds for four days to find out if there are symptoms of the flu.

If after four days, the farmer sees no symptoms of the flu in his birds, he might assume his birds are indeed free from bird flu whereas the bird flu might have affected his birds and the symptoms are obvious on the sixth day. 

By this indication, the farmer accepts that no flu exists in his birds. This leads to a type II error where it supports the null hypothesis when it is in fact false.

Frequently Asked Questions about Type I and II Errors

• Is a Type I or Type II error worse?

Both Type I and type II errors could be worse based on the type of research being conducted.

A Type I error means an incorrect assumption has been made when the assumption is in reality not true. The consequence of this is that other alternatives are disapproved of to accept this conclusion. A type II error implies that a null hypothesis was not rejected. This means that a significant outcome wouldn’t have any benefit in reality.

A Type I error however may be terrible for statisticians. It is difficult to decide which of the errors is worse than the other but both types of errors could do enough damage to your research. 

• Does sample size affect type 1 error?

Small or large sample size does not affect type I error . So sample size will not increase the occurrence of Type I error.

The only principle is that your test has a normal sample size. If the sample size is small in Type II errors, the level of significance will decrease.

This may cause a false assumption from the researcher and discredit the outcome of the hypothesis testing.

• What is statistical power as it relates to Type I or Type II errors

Statistical power is used in type II to deduce the measurement error. This is because random errors reduce the statistical power of hypothesis testing. Not only that, the larger the size of the effect, the more detectable the errors are.

The statistical power of a hypothesis increases when the level of significance increases. The statistical power also increases when a larger sample size is being tested thereby reducing the errors. If you want the risk of Type II error to reduce, increase the level of significance of the test.

• What is statistical significance as it relates to Type I or Type II errors

Statistical significance relates to Type I error. Researchers sometimes assume that the outcome of a test is statistically significant when they are not and the researcher then rejects the null hypothesis. The fact is, the outcome might have happened due to chance.

A type I error decreases when a lower significance level is set.

If your test power is lower compared to the significance level, then the alternative hypothesis is relevant to the statistical significance of your test, then the outcome is relevant.

In this article, we have extensively discussed Type I error and Type II error. We have also discussed their causes, the probabilities of their occurrence, and how to avoid them. We have seen that both Types of errors have their usefulness and limitations. The best approach as a researcher is to know which to apply and when.

Connect to Formplus, Get Started Now - It's Free!

• alternative vs null hypothesis
• hypothesis testing
• level of errors
• level of significance
• statistical hypothesis
• statistical power
• type i errors
• type ii errors
• busayo.longe

You may also like:

Hypothesis Testing: Definition, Uses, Limitations + Examples

The process of research validation involves testing and it is in this context that we will explore hypothesis testing.

Alternative vs Null Hypothesis: Pros, Cons, Uses & Examples

We are going to discuss alternative hypotheses and null hypotheses in this post and how they work in research.

Internal Validity in Research: Definition, Threats, Examples

In this article, we will discuss the concept of internal validity, some clear examples, its importance, and how to test it.

What is Pure or Basic Research? + [Examples & Method]

Simple guide on pure or basic research, its methods, characteristics, advantages, and examples in science, medicine, education and psychology

Formplus - For Seamless Data Collection

Collect data the right way with a versatile data collection tool. try formplus and transform your work productivity today..

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List

Curbing type I and type II errors

Kenneth j. rothman.

RTI Health Solutions, Research Triangle Park, NC USA

The statistical education of scientists emphasizes a flawed approach to data analysis that should have been discarded long ago. This defective method is statistical significance testing. It degrades quantitative findings into a qualitative decision about the data. Its underlying statistic, the P -value, conflates two important but distinct aspects of the data, effect size and precision [ 1 ]. It has produced countless misinterpretations of data that are often amusing for their folly, but also hair-raising in view of the serious consequences.

Significance testing maintains its hold through brilliant marketing tactics—the appeal of having a “significant” result is nearly irresistible—and through a herd mentality. Novices quickly learn that significant findings are the key to publication and promotion, and that statistical significance is the mantra of many senior scientists who will judge their efforts. Stang et al. [ 2 ], in this issue of the journal, liken the grip of statistical significance testing on the biomedical sciences to tyranny, as did Loftus in the social sciences two decades ago [ 3 ]. The tyranny depends on collaborators to maintain its stranglehold. Some collude because they do not know better. Others do so because they lack the backbone to swim against the tide.

Students of significance testing are warned about two types of errors, type I and II, also known as alpha and beta errors. A type I error is a false positive, rejecting a null hypothesis that is correct. A type II error is a false negative, a failure to reject a null hypothesis that is false. A large literature, much of it devoted to the topic of multiple comparisons, subgroup analysis, pre-specification of hypotheses, and related topics, are aimed at reducing type I errors [ 4 ]. This lopsided emphasis on type I errors comes at the expense of type II errors. The type I error, the false positive, is only possible if the null hypothesis is true. If the null hypothesis is false, a type I error is impossible, but a type II error, the false negative, can occur.

Type I and type II errors are the product of forcing the results of a quantitative analysis into the mold of a decision, which is whether to reject or not to reject the null hypothesis. Reducing interpretations to a dichotomy, however, seriously degrades the information. The consequence is often a misinterpretation of study results, stemming from a failure to separate effect size from precision. Both effect size and precision need to be assessed, but they need to be assessed separately, rather than blended into the P -value, which is then degraded into a dichotomous decision about statistical significance.

As an example of what can happen when significance testing is exalted beyond reason, consider the case of the Wall Street Journal investigative reporter who broke the news of a scandal about a medical device maker, Boston Scientific, having supposedly distorted study results [ 5 ]. Boston Scientific reported to the FDA that a new device was better than a competing device. They based their conclusion in part on results from a randomized trial in which the significance test showing the superiority of their device had a P -value of 0.049, just under the criterion of 0.05 that the FDA used statistical significance. The reporter found, however, that the P -value was not significant when calculated using 16 other test procedures that he tried. The P -values from those procedures averaged 0.051. According to the news story, that small difference between the reported P -value of 0.049 and the journalist’s recalculated P -value of 0.051 was “the difference between success and failure” [ 5 ]. Regardless of what the “correct” P -value is for the data in question, it should be obvious that it is absurd to classify the success or failure of this new device according to whether or not the P -value falls barely on one side or the other of an arbitrary line, especially when the discussion revolves around the third decimal place of the P -value. No sensible interpretation of the data from the study should be affected by the news in this newspaper report. Unfortunately, the arbitrary standard imposed by regulatory agencies, which foster that focus on the P -value, reduces the prospects for more sensible evaluations.

In their article, Stang et al. [ 2 ] not only describe the problems with significance testing, but also allude to the solution, which is to rely on estimation using confidence intervals. Sadly, although the use of confidence intervals is increasing, for many readers and authors they are used only as surrogate tests of statistical significance [ 6 ], to note whether the null hypothesis value falls inside the interval or not. This dichotomy is equivalent to the dichotomous interpretation that results from significance testing. When confidence intervals are misused in this way, the entire conclusion can depend on whether the boundary of the interval is located precisely on one side or the other of an artificial criterion point. This is just the kind of mistake that tripped up the Wall Street Journal reporter. Using a confidence interval as a significance test is an opportunity lost.

How should a confidence interval be interpreted? It should be approached in the spirit of a quantitative estimate. A confidence interval allows a measurement of both effect size and precision, the two aspects of study data that are conflated in a P -value. A properly interpreted confidence interval allows these two aspects of the results to be inferred separately and quantitatively. The effect size is measured directly by the point estimate, which, if not given explicitly, can be calculated from the two confidence limits. For a difference measure, the point estimate is the arithmetic mean of the two limits, and for a ratio measure, it is the geometric mean. Precision is measured by the narrowness of the confidence interval. Thus, the two limits of a confidence interval convey information on both effect size and precision. The single number that is the P -value, even without degrading it into categories of “significant” and “not significant”, cannot measure two distinct things. Instead the P -value mixes effect size and precision in a way that by itself reveals little about either.

Scientists who wish to avoid type I or type II errors at all costs may have chosen the wrong profession, because making and correcting mistakes are inherent to science. There is a way, however, to minimize both type I and type II errors. All that is needed is simply to abandon significance testing. If one does not impose an artificial and potentially misleading dichotomous interpretation upon the data, one can reduce all type I and type II errors to zero. Instead of significance testing, one can rely on confidence intervals, interpreted quantitatively, not simply as surrogate significance tests. Only then would the analyses be truly quantitative.

Finally, here is a gratuitous bit of advice for testers and estimators alike: both P -values and confidence intervals are calculated and all too often interpreted as if the study they came from were free of bias. In reality, every study is biased to some extent. Even those who wisely eschew significance testing should keep in mind that if any study were increased in size, its precision would improve and thus all its confidence intervals would shrink, but as they do, they would eventually converge around incorrect values as a result of bias. The final interpretation should measure effect size and precision separately, while considering bias and even correcting for it [ 7 ].

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

Advisory boards aren’t only for executives. Join the LogRocket Content Advisory Board today →

• Product Management
• Solve User-Reported Issues
• Find Issues Faster
• Optimize Conversion and Adoption

A guide to type 1 errors: Examples and best practices

When managing products, product managers often use statistical testing to evaluate the impact of new features, user interface adjustments, or other product modifications. Statistical testing provides evidence to help product managers make informed decisions based on data, indicating whether a change has significantly affected user behavior, engagement, or other relevant metrics.

However, statistical tests aren’t always accurate, and there is a risk of type 1 errors, also known as “false positives,” in statistics. A type 1 error occurs when a null hypothesis is wrongly rejected, even if it’s true.

PMs must consider the risk of type 1 errors when conducting statistical tests. If the significance level is set too high or multiple tests are performed without adjusting for multiple comparisons, the chance of false positives increases. This could lead to incorrect conclusions and waste resources on changes that don’t significantly affect the product.

In this article, you will learn what a type 1 error is, the factors that contribute to one, and best practices for minimizing the risks associated with it.

What is a type 1 error?

A type 1 error, also known as a “false positive,” occurs when you mistakenly reject a null hypothesis as true. The null hypothesis assumes no significant relationship or effect between variables, while the alternative hypothesis suggests the opposite.

For example, a product manager wants to determine if a new call to action (CTA) button implementation on a web app leads to a statistically significant increase in new customer acquisition.

The null hypothesis (H₀) states no significant effect on acquiring new customers on a web app after implementing a new feature, and an alternative hypothesis (H₁) suggests a significant increase in customer acquisition. To confirm their hypothesis, the product managers gather information on user acquisition metrics, like the daily number of active users, repeat customers, click through rate (CTR), churn rate, and conversion rates, both before and after the feature’s implementation.

After collecting data on the acquisition metrics from two different periods and running a statistical evaluation using a t-test or chi-square test, the PM * * falsely believes that the new CTA button is effective based on the sample data. In this case, a type 1 error occurs as he rejected the H₀ even though it has no impact on the population as a whole.

A PM must carefully interpret data, control the significance level, and perform appropriate sample size calculations to avoid this. Product managers, researchers, and practitioners must also take these steps to reduce the likelihood of making type 1 errors:

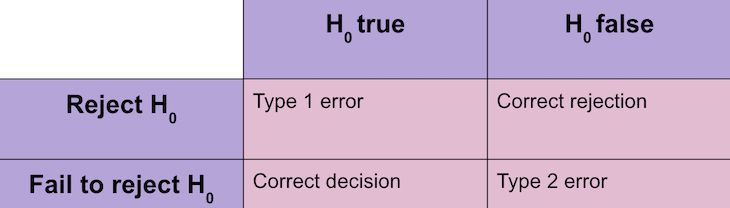
Type 1 vs. type 2 errors

Before comparing type 1 and type 2 errors, let’s first focus on type 2 errors . Unlike type 1 errors, type 2 errors occur when an effect is present but not detected. This means a null hypothesis (Ho) is not rejected even though it is false.

In product management, type 1 errors lead to incorrect decisions, wasted resources, and unsuccessful products, while type 2 errors result in missed opportunities, stunted growth, and suboptimal decision-making. For a comprehensive comparison between type 1 and type 2 errors with product development and management, please refer to the following:

To understand the comparison table above, it’s necessary to grasp the relationship between type 1 and type 2 errors. This is where the concept of statistical power comes in handy.

Statistical power refers to the likelihood of accurately rejecting a null hypothesis( Ho) when it’s false. This likelihood is influenced by factors such as sample size, effect size, and the chosen level of significance, alpha ( α ).

Over 200k developers and product managers use LogRocket to create better digital experiences

With hypothesis testing, there’s often a trade-off between type 1 and type 2 errors. By setting a more stringent significance level with a lower α, you can decrease the chance of type 1 errors, but increase the chance of Type 2 errors.

On the other hand, by setting a less stringent significance level with a higher α, we can decrease the chance of type 2 errors, but increase the chance of type 1 errors.

It’s crucial to consider the consequences of each type of error in the specific context of the study or decision being made. The importance of avoiding one type of error over the other will depend on the field of study, the costs associated with the errors, and the goals of the analysis.

Factors that contribute to type 1 errors

Type 1 errors can be caused by a range of different factors, but the following are some of the most common reasons:

Insufficient sample size

Multiple comparisons, publication bias, inadequate control groups or comparison conditions, human judgment and bias.

When sample sizes are too small, there is a greater chance of type 1 errors. This is because random variation may affect the observed results rather than an actual effect. To avoid this, studies should be conducted with larger sample sizes, which increases statistical power and decreases the risk of type 1 errors.

When multiple statistical tests or comparisons are conducted simultaneously without appropriate adjustments, the likelihood of encountering false positives increases. Conducting numerous tests without correcting for multiple comparisons can lead to an inflated type 1 error rate.

Techniques like Bonferroni correction or false discovery rate control should be employed to address this issue.

Publication bias is when studies with statistically significant results are more likely to be published than those with non-significant or null findings. This can lead to misleading perceptions of the true effect sizes or relationships. To mitigate this bias, meta-analyses or systematic reviews consider all available evidence, including unpublished studies.

More great articles from LogRocket:

• How to implement issue management to improve your product
• 8 ways to reduce cycle time and build a better product
• What is a PERT chart and how to make one
• Discover how to use behavioral analytics to create a great product experience
• Explore six tried and true product management frameworks you should know
• Advisory boards aren’t just for executives. Join LogRocket’s Content Advisory Board. You’ll help inform the type of content we create and get access to exclusive meetups, social accreditation, and swag.

When conducting experimental studies, selecting the wrong control group or comparison condition can lead to inaccurate results. Without a suitable control group, distinguishing the actual impact of the intervention from other variables becomes difficult, which raises the likelihood of making type 1 errors.

When researchers allow their personal opinions or assumptions to influence their analysis, they can make type 1 errors. This is especially true when researchers favor results that align with their expectations, known as confirmation bias.

To reduce the chances of type 1 errors, it’s crucial to consider these factors and utilize appropriate research design, statistical analysis methods, and reporting protocols.

Type 1 error examples

In software product management, minimizing type 1 errors is important. To help you better understand, here are some examples of type 1 errors from product management in the context of null hypothesis (Ho) validation, alongside strategies to mitigate them:

False positive impact of a new feature

False positive correlation between metrics, false positive for performance improvement, overstating the effectiveness of an algorithm.

Here, the assumption is that specific features of your software would greatly improve user involvement. To test this hypothesis, a PM conducts experiments and observes increased user involvement. However, it later becomes clear that the boost was not solely due to the feature, but also other factors, such as a simultaneous marketing campaign.

This results in a type 1 error.

Experiments focusing solely on the analyzed feature are important to avoid mistakes. One effective method is A/B testing , where you randomly divide users into two groups — one group with the new feature and the other without. By comparing the outcomes of both groups, you can accurately attribute any observed effects to the feature being tested.

In this case, a PM believes there is a direct connection between the number of bug fixes and customer satisfaction scores (CSAT) . However, after examining the data, you find a correlation that appears to support your hypothesis that could just be coincidental.

This leads to a Type 1 error, where bug fixes have no direct impact on CSAT.

It’s important to use rigorous statistical analysis techniques to reduce errors. This includes employing appropriate statistical tests like correlation coefficients and evaluating the statistical significance of the correlations observed.

Another potential instance comes when a hypothesis states that the performance of the software can be greatly enhanced by implementing a particular optimization technique. However, if the optimization technique is implemented and there is no noticeable improvement in the software’s performance, a type 1 error has occured.

To ensure the successful implementation of optimization techniques, it is important to conduct thorough benchmarking and profiling beforehand. This will help identify any existing bottlenecks.

A type 1 error occurs when an algorithm claims to predict user behavior or outcomes with high accuracy and then often falls short in real-life situations.

To ensure the effectiveness of algorithms, conduct extensive testing in real-world settings, using diverse datasets and consider various edge cases. Additionally, evaluate the algorithm’s performance against relevant metrics and benchmarks before making any bold claims.

Designing rigorous experiments, using proper statistical analysis techniques, controlling for confounding variables, and incorporating qualitative data are important to reduce the risk of type 1 error.

Best practices to minimize type 1 errors

To reduce the chances of type 1 errors, product managers should take the following measures:

• Careful experiment design — To increase the reliability of results, it is important to prioritize well-designed experiments, clear hypotheses, and have appropriate sample sizes
• Set a significance level — The significance level determines the threshold for rejecting the null hypothesis. The most commonly used values are 0.05 or 0.01. These values represent a 5 percent or 1 percent chance of making a type 1 error. Opting for a lower significance level can decrease the probability of mistakenly rejecting the null hypothesis
• Correcting for multiple comparisons — To control the overall type 1 error rate, statistical techniques like Bonferroni correction or the false discovery rate (FDR) can be helpful when performing multiple tests simultaneously, such as testing several features or variants
• Replication and validation — To ensure accuracy and minimize false positives, it’s important to repeat important findings in future experiments
• Use appropriate sample sizes — Sufficient sample size is important for accurate results. Determine the required size of the sample based on effect size, desired power, and significance level. A suitable sample size improves the chances of detecting actual effects and reduces type 2 errors

Product managers must grasp the importance of type 1 errors in statistical testing. By recognizing the possibility of false positives, you can make better evidence-based decisions and avoid wasting resources on changes that do not truly benefit the product or its users. Employing appropriate statistical techniques, considering effect sizes, replicating findings, and conducting rigorous experiments can help mitigate the risk of type 1 errors and ensure reliable decision-making in product management.

Featured image source: IconScout

LogRocket generates product insights that lead to meaningful action

Get your teams on the same page — try LogRocket today.

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Reddit (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on Facebook (Opens in new window)
• #product analytics
• #tools and resources

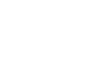
Stop guessing about your digital experience with LogRocket

Recent posts:.

Leader Spotlight: Making magic with the right SDLC model, with Trevor Riley

Trevor Riley talks about how adaptation is crucial to long-term success and how you need to adapt your software development life cycle.

Leader Spotlight: Enabling a cultural mind shift, with Nancy Wang

Nancy Wang shares how she’s spearheaded a “cultural mind shift” away from an IT plan-build-run organization to a product-centric one.

A guide to decentralized decision-making

Decentralized decision-making is the process where stakeholders distribute strategic decisions within an organization to lower-level teams.

Cumulative flow diagrams: Unraveling Kanban metrics

A cumulative flow diagram is an advanced analytic tool that represents the stability of your workflow over time.

Leave a Reply Cancel reply

Learn / Guides / CRO glossary

Back to guides

CRO glossary: type 1 error

What is a type 1 error?

Type 1 error is a term statisticians use to describe a false positive—a test result that incorrectly affirms a false statement about the nature of reality.

In  A/B testing , type 1 errors occur when experimenters falsely conclude that any variation of an A/B or  multivariate test  outperformed the other(s) due to something more than random chance. Type 1 errors can hurt conversions when companies make website changes based on incorrect information.

Type 1 errors vs. type 2 errors

While a type 1 error implies a false positive—that one version outperforms another—a type 2 error implies a false negative. In other words, a type 2 error falsely concludes that there is no  statistically significant  difference between conversion rates of different variations when there actually  is  a difference.

Here’s what that looks like:

What causes type 1 errors?

Type 1 errors can result from two sources: random chance and improper research techniques. 

Random chance:  no random sample, whether it’s a pre-election poll or an A/B test, can ever perfectly represent the population it intends to describe. Since researchers sample a small portion of the total population, it’s possible that the results don’t accurately predict or represent reality—that the conclusions are the product of random chance.

Statistical significance  measures the odds that the results of an A/B test were produced by random chance. For example, let’s say you’ve run an A/B test that shows Version B outperforming Version A with a statistical significance of 95%. That means there’s a 5% chance these results were produced by random chance.You can raise your level of statistical significance by increasing the sample size, but this requires more traffic and therefore takes more time. In the end, you have to strike a balance between your desired level of accuracy and the resources you have available. 

Improper research techniques : when running an A/B test, it’s important to gather enough data to reach your desired level of statistical significance. Sloppy researchers might start running a test and pull the plug when they feel there’s a ‘clear winner’—long before they’ve gathered enough data to reach their desired level of statistical significance. There’s really no excuse for a type 1 error like this.

Why are type 1 errors important?

Type 1 errors can have a huge impact on conversions. For example, if you A/B test two page versions and incorrectly conclude that version B is the winner, you could see a massive drop in conversions when you take that change live for all your visitors to see. As mentioned above, this  could  be the result of poor experimentation techniques, but it might also be the result of random chance. Type 1 errors can (and do) result from flawless experimentation.

When you make a change to a webpage based on A/B testing, it’s important to understand that you may be working with incorrect conclusions produced by type 1 errors. 

Understanding type 1 errors allows you to:

Choose the level of risk you’re willing to accept (e.g., increase your sample size to achieve a higher level of statistical significance)

Do proper experimentation to reduce your risk of human-caused type 1 errors 

Recognize when a type 1 error may have caused a drop in conversions so you can fix the problem 

It’s impossible to achieve 100% statistical significance (and it’s usually impractical to aim for 99% statistical significance, since it requires a disproportionately large sample size compared to 95%-97% statistical significance). The goal of CRO isn’t to get it right every time—it’s to make the right choices  most  of the time. And when you understand type 1 errors, you increase your odds of getting it right. 

How do you minimize type 1 errors?

The only way to minimize type 1 errors, assuming you’re A/B testing properly, is to raise your level of statistical significance. Of course, if you want a higher level of statistical significance, you’ll need a larger sample size.

It isn’t a challenge to study large sample sizes if you’ve got massive amounts of traffic, but if your website doesn’t generate that level of traffic, you’ll need to be more selective about what you decide to study—especially if you’re going for higher statistical significance.

Here’s how to narrow down the focus of your experiments.

6 ways to find the most important elements to test

In order to test what matters most, you need to determine what really matters to your target audience. Here are six ways to figure out what’s worth testing.

Read reviews and speak with your Customer Support department : figure out what people think of your brand and products. Talk to Sales, Customer Support, and Product Design to get a sense of what people really want from you and your products.

Figure out why visitors leave without buying:   traditional analytics  tools (e.g., Google Analytics) can show where people leave the site. Combining this data with Hotjar’s  Conversion Funnels Tool  will give you a strong sense of which pages are worth focusing on.

Discover the page elements that people engage :  heatmaps  show where the majority of users click, scroll, and hover their mouse pointers (or tap their fingers on mobile devices and tablets). Heatmaps will help you find trends in how visitors interact with key pages on your website, which in turn will help you decide which elements to keep (since they work) and which ones are being ignored and need further examination.

Gather feedback from customers : on-page surveys,  polls , and feedback widgets give your customers a way to quickly send feedback about their experience your way. This will alert you to issues you never knew existed and will help you prioritize what needs fixing for the experience to improve.

Look at   session recordings : see how individual (anonymized) users behave on your site. Notice where they struggle and how they go back and forth when they can’t find what they need.  Pro tip : pay particular attention to what they do just  before  they leave your site.

Explore usability testing : can help you understand how people see and experience your website. Capture spoken feedback about issues they encounter, and discover what could improve their experience.

Pro tip : do you want to improve  everyone’s  experience? That may be tempting, but you’ll get a whole lot further by focusing on your ideal customers. To learn more about identifying your ideal customers, check out our blog post about  creating simple user personas .

Find the perfect elements to A/B test

Use Hotjar to pinpoint the right elements to test—those that matter most to your target market.

Statistical significance

Previous chapter

Unique selling proposition

Next chapter

Comparing type 1 and type 2 error rates of different tests for heterogeneous treatment effects

• Original Manuscript
• Open access
• Published: 20 March 2024

Cite this article

You have full access to this open access article

• Steffen Nestler 1 &
• Marie Salditt 1  

115 Accesses

2 Altmetric

Explore all metrics

Psychologists are increasingly interested in whether treatment effects vary in randomized controlled trials. A number of tests have been proposed in the causal inference literature to test for such heterogeneity, which differ in the sample statistic they use (either using the variance terms of the experimental and control group, their empirical distribution functions, or specific quantiles), and in whether they make distributional assumptions or are based on a Fisher randomization procedure. In this manuscript, we present the results of a simulation study in which we examine the performance of the different tests while varying the amount of treatment effect heterogeneity, the type of underlying distribution, the sample size, and whether an additional covariate is considered. Altogether, our results suggest that researchers should use a randomization test to optimally control for type 1 errors. Furthermore, all tests studied are associated with low power in case of small and moderate samples even when the heterogeneity of the treatment effect is substantial. This suggests that current tests for treatment effect heterogeneity require much larger samples than those collected in current research.

Similar content being viewed by others

Compensation and Amplification of Attenuation Bias in Causal Effect Estimates

Marie-Ann Sengewald & Steffi Pohl

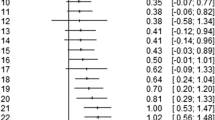
A group-specific prior distribution for effect-size heterogeneity in meta-analysis

Christopher G. Thompson & Betsy Jane Becker

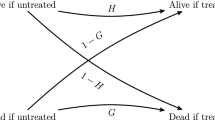
Effect heterogeneity and variable selection for standardizing causal effects to a target population

Anders Huitfeldt, Sonja A. Swanson, … Etsuji Suzuki

Avoid common mistakes on your manuscript.

In the last decades, psychologists have conducted a large number of randomized controlled trials and observational studies to test the effectiveness of specific interventions, such as, for example, an educational support program or a psychotherapy (Kravitz et al., 2004 ). In almost all of these studies, the parameter of interest is the average treatment effect, a measure of the overall impact of treatment. However, researchers and practitioners know that treatment effects can be highly heterogeneous across study participants. For example, students with a low social status may benefit more from an educational support program than students with a higher social status, or certain patients may respond more to a specific treatment than other patients.

Knowing the variables that are responsible for the heterogeneity in treatment effects is very interesting from an applied perspective because this would allow to better tailor the results of randomized controlled trials to particular persons (e.g., to identify the right educational support program for a student or the right treatment for a patient; see Deaton & Cartwright, 2018 , but also Cook, 2018 ). Hence, there is a growing interest in statistical approaches that allow to detect whether – and if so, why – treatment effects vary in randomized controlled trials. Specifically, multiple methods have been suggested for detecting how the treatment effect varies based on variables that are measured prior to treatment. Among these approaches are standard linear methods such as the moderated regression model (Cox, 1984 ), but also different machine learning methods such as causal forests (Athey et al., 2019 ), causal boosting (Powers, Qian, and et al., 2018 ), and various meta-learners (e.g., the S-Learner, the T-Learner, or the X-Learner, see Künzel et al., 2019 ; Salditt et al., 2023 ; Wendling et al., 2018 ).

However, in some settings, the relevant variables may not have been measured, so that these methods cannot be applied. Then, researchers may simply want to assess whether the average treatment effect observed in their randomized controlled trial varies across participants to such a degree that it is of substantive importance. If it does not, this would indicate that the treatment can be applied to all individuals. Conversely, if it does vary, this would indicate the need for further research to investigate which variables are driving the heterogeneity. A number of tests have been proposed to assess the null hypothesis of homogeneity of treatment effects in the causal inference literature to answer this question. Despite the increasing focus on heterogeneity of treatment effects, only some of these tests are known in psychology (see Kaiser et al., 2022 for a meta-analytic application of one of these tests), and to date there are no simulation studies that have examined and compared the performance of all of these tests in different settings.

In this article we aim to present the different tests suggested in the causality literature for detecting heterogeneous treatment effects. Furthermore, we conducted a simulation study to examine their performance subject to the amount of treatment effect heterogeneity, the sample size, and the inclusion of an additional covariate when performing the test. In the following, we first introduce the average treatment effect using the potential outcomes framework (Imbens & Rubin, 2015 ). We then describe the different test procedures to test the null hypothesis that the average treatment effect is constant across persons. Afterwards, we present the results of the simulation study, and then conclude with a discussion of the results and questions for future research.

Potential outcome framework and heterogeneous treatment effects

We use the potential outcome framework to define homogeneous and heterogeneous treatment effects (see Hernan & Robins, 2020 ; Imbens & Rubin, 2015 ; Rosenbaum, 2010 for introductions). To this end, let \(A_i\) be the binary treatment variable with 0 indicating that person i is in the control group and 1 that she is in the experimental group. The potential outcome corresponding to the outcome person i would have experienced had she received the treatment is denoted by \(Y_{i}(1)\) and the outcome had she been in the control condition is \(Y_{i}(0)\) . The causal effect of the treatment for the i th person then is

The stable unit treatment value assumption (SUTVA, see Imbens & Rubin2015, 2015 ; Rosenbaum, 2002 ) entails that the observed outcome equals the potential outcome under the condition actually received:

Since a single person i can only be assigned to either the experimental or the control group, only \(Y_{i}(1)\) or \(Y_{i}(0)\) can be observed, such that it is impossible to observe \(\tau _{i}\) (see Holland, 1986 ). However, under certain additional assumptions, such as the assumption that the potential outcomes are independent from treatment (i.e., \(A_{i} \perp \!\!\!\!\perp \lbrace Y_{i}(0),Y_{i}(1) \rbrace \) ), we can estimate the average of each potential outcome using the average of the observed outcome values in the experimental and control group, respectively:

This in turn allows to estimate the average of the individual treatment effects:

When the treatment effect is homogeneous across all persons, that is, \(\tau _{i} = \tau \) for all \(i = 1, \dots , n\) , the average treatment effect equals the constant effect, \(\mathbb {E}[\tau _{i}] = \tau \) . Thus, the treatment increases the mean difference between the experimental and control group by amount \(\tau \) :

Tests for heterogeneous treatment effects

The goal of all test procedures suggested in the causal inference literature is to test the null hypothesis that the treatment effect is constant for all persons:

The proposed tests differ in the sample statistics they use and in whether they make distributional assumptions for the potential outcomes. Concerning sample statistics, the different tests use estimates of the variance parameters in the control and the experimental group, the empirical distribution functions of the two groups, or they compare a grid of quantiles estimated in the two groups. Concerning the distributional assumptions, some tests presume that the potential outcomes, and therefore the observed outcomes, are normally distributed, while other tests belong to the class of Fisher randomization tests (FRT) that do not rely on any distributional assumptions (Imbens & Rubin, 2015 ; Rosenbaum, 2002 ).

Comparing variance terms

There are several ways to implement a comparison of variance terms for testing treatment effect heterogeneity. All of these tests are based on the observation that when the treatment effect is constant across persons, it does not influence the variance of the potential outcomes:

where the first equality follows from Eq. 1 and the second uses the fact that the variance of a constant is zero. Under the assumptions introduced above, \(\mathbb {V}[Y_{i}(1)]\) and \(\mathbb {V}[Y_{i}(0)]\) equal the variance of the observed values in the experimental and the control group, respectively:

Variance ratio

Using Eq. 8 , a potential test statistic to test for treatment effect heterogeneity consists of computing the ratio of the two estimates of the aforementioned variance terms:

When we assume that each potential outcome is normally distributed, \(T_{V}\) is F -distributed with degrees of freedom \(n_{1} - 1\) and \(n_{0} - 1\) and testing \(T_{V}\) equals the F -test for two variance terms (e.g., Casella & Berger, 2002 ). Alternatively, one can use a heterogeneous regression model in which the residual variance is modeled as a function of the treatment variable (Bloome & Schrage, 2021 ; Western & Bloome, 2009 ):

Here, the estimate \(\hat{\gamma }_1\) measures the difference between the variance of the two groups on a log-scale and a test statistic \(T_{\gamma }\) is obtained by dividing \(\hat{\gamma }_1\) by its standard error. The resulting test statistic can be used to test the presence of a heterogeneous treatment effect (Bloome & Schrage, 2021 ), and we will simply refer to this test as \(T_{\gamma }\) in the simulation study reported later. Importantly, \(\hat{\gamma }_1\) equals \(T_{V}\) after exponentiation, which is why we only consider \(T_{\gamma }\) and not the F -test for \(T_{V}\) as variance-ratio-based test that assumes normally distributed data, because the two tests yield the same decision concerning the null hypothesis.

A test that does not rely on such distributional assumptions can be obtained when using \(T_{V}\) in a Fisher randomization test (FRT, Imbens & Rubin, 2015 ; Rosenbaum, 2002 ; 2010 ). The basis of the FRT is that – given the aforementioned null hypothesis – the missing potential outcome values can be imputed assuming that we know the treatment effect. Thus, when person i belongs to the experimental group, her observed value is \(Y_i = Y_i(1)\) and the missing potential outcome is \(Y_i(0) = Y_i(1) - \tau = Y_i - \tau \) . Alternatively, when person i is in the control group, her missing potential outcome is \(Y_i(1) = Y_i + \tau \) .

Using this, the FRT constructs a sampling distribution of the test statistic ( \(T_{V}\) in this case) by randomly permuting the observed values of the treatment variable . To illustrate, when the observed treatment values are 0, 1, 1, 0, 0, and 1 for person one to six, a randomly permuted treatment variable would be 1, 0, 0, 1, 1, and 0. The test statistic is then computed again using the group assignments in the permuted treatment variable. This process is repeated a large number of times (e.g., B = 1000) and the resulting distribution of the test statistic (e.g., the distribution of the \(T_{V}\) values) is used to obtain a p  value by computing the relative frequency of the values of the test statistic that are greater than the observed test statistic:

where \(T_{\textrm{obs}}\) is the observed test statistic (i.e., \(T_{V}\) here) and \(T_j\) is the value of the test statistic in the j th randomization sample. As said above, the basis of the FRT is that given the null hypothesis of a constant treatment effect, the missing potential outcome values can be imputed assuming that one knows the true average treatment effect. In case of \(T_{V}\) the assumption of knowing the true treatment effect is not important, because the test compares two variance parameters that – given the null hypothesis – are not affected by the ‘constant’ \(\tau \) .

Variance difference

\(T_{V}\) and \(T_{\gamma }\) use the ratio of the two variance terms. Another way to test the null hypothesis of a constant treatment effect consists of taking the absolute difference between the two variance terms

and to use \(T_{D}\) in a FRT (we refer to this test as \(T_{D}\) in the simulation study reported later). Alternatively, when one assumes normally distributed potential outcomes, one can implement a test of the variance difference in a random coefficient regression model or in the multiple group structural equation model framework. In a random coefficient regression model, the slope of a predictor variable is allowed to vary across individuals (as in the case of a multilevel model), although only one score is available for a single participant (in econometrics this model is called the Hildreth–Houck model, see Hildreth & Houck, 1968 ; Muthén et al., 2017 ). Applied to the present context, the slope of the treatment variable is modeled to differ between persons:

where \(u_i\) is a normally distributed error term with expectation zero and variance \(\sigma _{u}^{2}\) . When the (normally distributed) error term is uncorrelated with \(u_i\) , the conditional variance of \(y_i\) is given by

Thus, the variance in the control group is \(\mathbb {V}[y_{i}|A_i = 0] = \sigma _{\epsilon }^{2}\) and in the experimental group the variance is \(\mathbb {V}[y_{i}|A_i = 1] = \sigma _{u}^{2} + \sigma _{\epsilon }^{2}\) , showing that the difference between the two is \(\sigma _{u}^{2}\) . When we fit the model to the data (using Mplus, see below and Muthen & Muthen, 1998-2017 ), a Wald test can then be employed to check whether the sample estimate \(\hat{\sigma }_{u}^{2}\) is significantly different from zero. In the simulation study, we call this test \(T_{\beta }\) .

The second way to implement the variance difference test when assuming normally distributed data is to use a multiple group structural equation model (Tucker-Drob, 2011 ). Specifically, one fits a structural equation model to the data of the experimental group and another one to the control group and compares the fit of this unconstrained multiple group model to the fit of a constrained multiple group model in which the variance terms of the outcome variable are restricted to be equal. Formally, the fit of the two models is compared using a chi-squared difference test that is a likelihood-ratio (LR) test. The LR-test is asymptotically equivalent to a Wald-test that compares the difference between the two variance terms (Bollen, 1989 ; Muthén et al., 2017 ). Later, we abbreviate this test with \(T_{LR}\) .

Variance ratio and variance differences with rank data

All tests described so far use the observed data to compute the respective test statistic. However, in the case of testing the null hypothesis of no average treatment effect, simulation studies showed that a FRT that uses rank data has good error rates across different simulation conditions (Imbens & Rubin, 2015 ; Rosenbaum, 2002 , 2010 ). To conduct such a rank-based FRT, one first transforms the outcome to ranks and then computes the test statistic on the resulting rank data. To examine whether the good performance of the rank-based FRTs for testing the average treatment effects against zero generalizes to the context of heterogeneous treatment effects, we also consider rank-based versions of the FRTs in the simulation study (referred to as \(T^{R}_{V}\) and \(T^{R}_{D}\) , respectively).

Comparing the cumulative distribution functions

A second group of tests is based on the two-sample Kolmogorov–Smirnov test statistic. The idea is to compare the marginal distribution function in the control group with the marginal distribution function in the experimental group, because under the null hypothesis of a constant treatment effect, the two distribution functions differ only by the average treatment effect \(\tau \) . Thus, if \(\tau \) would be known, one could use (Ding et al., 2016 )

where \(\hat{F}_{0}\) and \(\hat{F}_{1}\) denotes the empirical cumulative distribution functions of the outcome in the control and experimental group, respectively. \(T_{\textrm{KS}}\) presumes that the true treatment effect \(\tau \) is known. Because this is not the case, an obvious fix would be to use the estimated average treatment effect \(\hat{\tau }\) , resulting in the ’shifted’ test statistic:

However, (Ding et al., 2016 ) show that the sampling distribution of \(T_{\textrm{SKS}}\) is not equivalent to the sampling distribution of the standard KS test statistic (see Wasserman, 2004 for the function) and therefore yields either inflated or deflated false-positive and false-negative error rates. To deal with this problem, they suggest to use \(T_{\textrm{SKS}}\) in a FRT. To this end, one first computes the potential outcomes \(Y_{i}(0)\) and \(Y_{i}(1)\) for each participant by plugging in the estimated average treatment effect \(\hat{\tau }\) . That is, \(Y_{i}(0) = Y_i\) and \(Y_{i}(1) = Y_i + \hat{\tau }\) for the persons in the control group, and \(Y_{i}(0) = Y_i - \hat{\tau }\) and \(Y_{i}(1) = Y_i\) for the persons in the experimental group. These potential outcomes are then used as the basis for the FRT in which \(T_{\textrm{SKS}}\) is computed in each randomization sample. The resulting distribution of the \(T_{\textrm{SKS}}\) scores is then used to test the null hypothesis (see Eq. 11 ).

Ding et al. ( 2016 ) call this the FRT-Plug in test (henceforth, FRT-PI) and argue that the procedure should yield valid results when the estimated average treatment effect is close to the true average treatment effect (e.g., when the sample size is large). However, as there are no guarantees that this is the case, Ding et al. ( 2016 ) suggest a second FRT in which not only one value for the hypothesized constant treatment effect is plugged in, but rather a range of plausible average treatment effects. Specifically, they suggest to construct a 99.9% confidence interval for the estimated average treatment effect and to use a grid of values covering this interval in the FRT. That is, for each of these treatment effects, the FRT is performed and one then finds the maximum p  value over all the resulting randomization tests. When this p  value is smaller than the significance level, one rejects the null hypothesis. Following Ding et al. ( 2016 ), we henceforth call this test FRT-CI.

Comparing quantiles

A third test was suggested by Chernozhukov & Fernandez-Val ( 2005 ) and is based on a comparison of quantiles instead of the cumulative distribution functions. Specifically, the test is based on the observation that

where \(F^{-1}_{0}\) and \(F^{-1}_{1}\) is the inverse of the cumulative distribution function in the control and experimental group, respectively, q is a certain quantile, and \(\tau (q)\) is the average treatment effect at the q th quantile. When the null hypothesis of a constant treatment effect is true, \(\tau (q)\) would be constant across all quantiles q . Therefore, Chernozhukov & Fernandez-Val ( 2005 ) suggest testing the null hypothesis with a type of KS-statistic in which one first obtains estimates of the treatment effect at certain quantiles and then takes the largest difference between these values and the average treatment effect:

In their implementation of the test, Chernozhukov & Fernandez-Val ( 2005 ) use quantile regression (Hao & Naiman, 2007 ), in which the outcome Y is regressed on the treatment indicator A at a quantile q , to obtain an estimate of \(\hat{\tau }(q)\) .

Similar to the shifted KS statistic (see Eq. 16 ), \(T_{\textrm{sub}}\) uses an estimate of the true average treatment effect. Therefore, Chernozhukov & Fernandez-Val ( 2005 ) suggest to use a subsampling approach to obtain a valid test statistic. In subsampling, the sampling distribution of a statistic is obtained by drawing subsamples of a certain size b without replacement from the current dataset. In each subsample, the respective statistic is computed ( \(T_{\textrm{sub}}\) in our case) and the resulting sampling distribution is then used – similar to the bootstrap – for inferences concerning the statistic. Chernozhukov & Fernandez-Val ( 2005 ) show that their subsampling approach is asymptotically correct. They also found their approach to yield valid type 1 error rates in a simulation study.

Comparing coefficients of variation

Finally, it was also suggested to compare the coefficients of variation (CV) instead of the variance terms to detect heterogeneous treatment effects (Nakagawa et al., 2015 ; Volkmann et al., 2020 ), because the magnitude of the variance depends on the mean (e.g., the larger the mean on a bounded scale, the lower a variable’s reachable variance). The coefficient of variation is the ratio of the standard deviation \(\sigma \) of a variable to its mean \(\mu \)

and a potential test statistic then is to compare the estimated CVs from the two groups

However, a problem with using \(T_{CV}\) is that the test statistic is not only affected by a heterogeneous treatment effect (e.g., \(\hat{\sigma }_{1} \ne \hat{\sigma }_{0}\) ), but also by whether there is a nonzero average treatment effect. For instance, when \(\hat{\sigma }_{1}\) = \(\hat{\sigma }_{0}\) = 1 and \(\hat{\mu }_{1} = \hat{\mu }_{0} + 1\) , then \(T_{CV}\) would be equal to 0.5. Thus, \(T_{CV}\) cannot be used to test the null hypothesis of a constant treatment effect, at least when the average treatment effect is nonzero. Footnote 1 Therefore, we do not consider this test statistic in our simulation.

Considering covariates

So far we assumed that data is available for the treatment variable and the outcome only. However, when a randomized controlled trial is conducted in practice, researchers may also have assessed a number of person-level pretreatment covariates. When testing the average treatment effect against zero, it is well known (e.g., Murnane & Willett, 2011 ) that considering these covariates in the model can increase the precision of the treatment effect estimate and power. In a similar way, considering covariates may help to increase the power of the treatment heterogeneity tests.

In case of the test based on the heterogeneous regression model ( \(T_{\gamma }\) , see Eq. 10 ), the random coefficient model ( \(T_{\beta }\) , see Eq. 13 ), and the structural equation model ( \(T_{LR}\) ), one can consider such covariates by including them as predictors of the outcome variable. Footnote 2 For the other tests, the outcome variable is first regressed on the covariates. The residuals of this regression can then be used in the FRT approaches or in the tests based on the cumulative distribution function. In the latter case, one then computes a ‘regression-adjusted KS statistic’ (cf., Ding et al., 2016 ). For the quantile-based test (i.e., \(T_{\textrm{sub}}\) ), Koenker and Xiao ( 2002 ) suggested to estimate \(\tau (q)\) in a quantile regression of the outcome on the treatment variable and the covariates and to use these estimates when computing \(T_{\textrm{sub}}\) .

The present research

The foregoing discussion showed that a number of tests were proposed in the causal inference literature to test for heterogeneity in treatment effects (see Table 1 for a summary) and simulation studies conducted so far found that some of the proposed tests keep their nominal type 1 error rates while also preserving low type 2 error rates. Bloome and Schrage ( 2021 ), for example, examined the performance of \(T_{\gamma }\) in case of normally distributed potential outcomes and a sample size of 200 or 1000 persons per group. They found that \(T_{\gamma }\) has good type 1 error rates at both sample sizes and that the type 2 error rate gets smaller the larger the size of the two groups. Ding et al. ( 2016 ) compared their proposed FRT approaches (i.e., FRT-PI and FRT-CI) with the subsampling approach of (Chernozhukov & Fernandez-Val, 2005 ) at sample sizes of 100 or 1000 persons in each group. When the treatment effect is homogeneous, all three tests yielded good type 1 error rates. Furthermore, the power of the tests to detect heterogeneous treatment effects was low for all three methods when the size of the samples was small. However, as expected, the power increased with increasing sample sizes and with increasing treatment effect heterogeneity.

The simulation study reported here is aimed at replicating and extending these results. Specifically, we conducted the simulation study with four purposes. First, in our review we described several tests whose suitability for testing treatment effect heterogeneity has not yet been investigated (e.g., the random coefficient model, rank-based FRTs), neither alone nor in comparison to the other tests. We wanted to compare all of the proposed tests in one simulation study, rather than evaluating a subset of the tests only. We believe that this is important because so far psychologists often compare – if at all – the variance terms to test the presence of heterogeneous treatment effects and seldomly use (rank-based) FRT versions. Thus, if the other tests have higher power, applied researchers would currently make a type 2 error unnecessarily often (i.e., they would underestimate the frequency of heterogeneous treatment effects). Second, we wanted to examine the error rates at smaller sample sizes. So far, sample sizes of 100, 200, or 1000 persons per group have been investigated. However, randomized controlled trials sometimes involve fewer persons per condition and it is thus important to evaluate the performance of the tests at such smaller sample sizes. Third, to the best of our knowledge, there is no simulation study that has investigated whether and to what extent the inclusion of covariates affects the power of the various tests. Finally, we also wanted to investigate whether (and how) the error rates are affected when variables are not normally distributed, but stem from distributions in which more extreme values can occur, or which are skewed.

Simulation study

We performed a simulation study to assess the type 1 and type 2 error rates in different sample size conditions and in different conditions of treatment effect heterogeneity. We also varied the size of the average treatment effect and the distribution of the potential outcomes, and we examined whether the consideration of a covariate increase the power of the tests. The R code for the simulation study can be found at https://osf.io/nbrg2/ .

Simulation model and conditions

The population model that we used was inspired by the model used in Chernozhukov and Fernandez ( 2005 ) and Ding et al. ( 2016 ). Specifically, the model used to generate the data was an additive treatment effect model:

To manipulate the size of the heterogeneous treatment effect, we followed (Ding et al., 2016 ) by setting \(\sigma _{\tau }\) to 0, 0.25, or 0.5, corresponding to a constant treatment effect across participants, a moderate, or a large heterogeneous treatment effect. Although no conventions with regard to the size of heterogeneous treatment effect exist, we call the two conditions moderate and large, because setting \(\sigma _{\tau }\) to 0.25 (0.50) implies that the variance in the experimental group is about 1.5 (2) times larger than the variance in the control group (i.e., \(\sigma ^2_{0} = 1\) vs. \(\sigma ^2_{1} = 1.56\) and \(\sigma ^2_{1} = 2.25\) , respectively). To manipulate the type of underlying distribution, \(\epsilon _{i}\) was generated from a standard normal distribution (i.e., \(\epsilon _{i} \sim \mathcal {N}(0,1)\) ), from a t -distribution with 5 degrees of freedom, or from a log-normal distribution with mean 0 and standard deviation 1 (both on a log-scale). The t -distribution is a symmetric distribution that has thicker tails compared to the normal distribution. The chance that extreme values occur in a random sample are thus larger. The log-normal distribution, by contrast, is an asymmetric distribution. Using this distribution thus allows us to examine how skewness of the data influences the five tests. Furthermore, the average treatment effect \(\tau \) was set to either 0 or 1. The latter manipulation was examined to examine whether the performance of the tests is affected by the presence of an nonzero average treatment effect and we set \(\tau \) to this rather large value (i.e., in the normal case the implied d is 1) to not miss any effects that an (incorrect) estimation of the average treatment effect might have.

The number of participants was set to 25, 50, 100, or 250 in each group. A sample size of 25 per group is a rather small sample size for a randomized controlled trial and 250 participants per group can be considered a large sample (reflecting, for example, the growing number of multi-center studies). The other two sample sizes are in between and were included to examine the error rates in case of more moderate sample sizes. Finally, to examine the effect of including a covariate on the power of the tests, we generated a standard normal variable \(X_i\) and used

to generate \(Y_{i}(0)\) in the first step of the respective conditions. In the case where \(\epsilon _{i}\) is drawn from a standard normal distribution, this implies that the correlation between \(X_i\) and each of the potential outcomes is 0.30, which corresponds to a moderate effect.

Tests and dependent variables

For each of the 3 (size of heterogeneity) \(\times \) 3 (type of distribution) \(\times \) 2 (zero versus nonzero average treatment effect) \(\times \) 4 (no. of participants in a group) \(\times \) 2 (zero versus nonzero covariate) = 144 conditions, we generated 1000 simulated data sets. For each condition, the 1000 replications were analyzed by computing the ten test statistics, that is, \(T_{\gamma }\) , \(T_{V}\) , \(T^{R}_{V}\) , \(T_{LR}\) , \(T_{\beta }\) , \(T_{D}\) , \(T^{R}_{D}\) , FRT-PI, FRT-CI, and \(T_{\textrm{sub}}\) . Footnote 3 \(T_{V}\) , \(T^{R}_{V}\) , \(T_{D}\) , and \(T^{R}_{D}\) were each implemented as a FRT. We used B = 2000 randomization samples to obtain the sampling distribution of the statistic in each replication. This distribution was then used to obtain the p  value for this replication. When the p  value was smaller than \(\alpha = .05\) , the null hypothesis of a constant treatment effect was rejected, otherwise it was accepted.

We used the functions of Ding et al. ( 2016 ) to compute the FRT-PI and the FRT-CI, respectively. For both tests, we proceeded the same way as for \(T_{V}\) , but with the difference that we followed the suggestions of Ding et al. ( 2016 ) and set the number of randomization samples to B = 500. In case of FRT-CI, a grid of 150 values was used to compute the maximum p  value (this is the default value in the functions of Ding et al. 2016 ). \(T_{\gamma }\) was obtained by regressing the treatment variable on the outcome variable in a regression model. Furthermore, the residual variance of this model (see Eq. 10 ) was also modeled as function of the treatment variable and the latter coefficient was used to test for heterogeneous treatment effects. Specifically, if the absolute value of the estimate divided by its standard error was greater than 1.96, the null hypothesis of a constant treatment effect was counted as rejected. The heterogeneous regression model was estimated using remlscore function in the R package statmod (Giner & Smyth, 2016 ). We used Mplus (Muthén & Muthén, 1998-2017 ) to compute the random coefficient regression model to obtain \(T_{\beta }\) . Mplus implements a maximum likelihood estimator for the model’s parameters (see, Muthén et al., 2017 . In the simulation, we used the R package MplusAutomation (Hallquist & Wiley, 2018 ) to control Mplus from R. To obtain \(T_{LR}\) , we fitted two multiple group structural equation models with the lavaan package (Rosseel, 2012 ). The first model was an unconstrained model, in which the variance of the outcome variable in the experimental and the control group were allowed to differ, and in the second, constrained model, they were restricted to be equal. The LR-test is then obtained by comparing the fit of the two models with a chi-square difference test. Finally, we used the functions of Chernozhukov and Fernandez-Val ( 2005 ) with their default settings to obtain \(T_{\textrm{sub}}\) (resulting in a subsampling size of \(b \approx \) 20).

In each replication, we determined whether a test statistic rejected the null hypothesis of a constant treatment effect and used this information to calculate the rejection rate per simulation condition. When the standard deviation \(\sigma _{\tau }\) is 0, this rate measures the type 1 error rate. If \(\sigma _{\tau }\) is greater than 0, the rejection rate is an indicator of the power of a test.

We first discuss the results for the case that no covariate was considered in the tests. The results for the different tests concerning the two error rates were very similar for an average treatment effect of zero and one. Therefore, we focus on the results for the conditions of a zero average treatment effect here and later discuss some noticeable differences from the conditions in which the treatment effect is one.

Table 2 presents the results concerning type 1 error and power rates when no covariate was considered when performing the tests. Turning to the number of type 1 errors first (i.e., the columns with \(\sigma _{\tau } = 0\) ), \(T_{V}\) \(T_{V}^{R}\) , \(T_{D}\) , \(T_{D}^{R}\) , \(T_{\gamma }\) , \(T_{LR}\) and the FRT-PI yielded exact or almost exact rejection rates when the potential outcomes were normally distributed, irrespective of the size of the two groups. For FRT-CI, \(T_{\textrm{sub}}\) , and \(T_{\beta }\) the rates were too conservative, but they almost approached the nominal \(\alpha \) -level as the sample size increased. When the data followed a t -distribution, all FRT-based except FRT-CI tests (i.e., \(T_{V}\) , \(T_{V}^{R}\) , \(T_{D}\) , \(T_{D}^{R}\) , FRT-PI) were still near the nominal value. For the latter, the type 1 error rate again approached the nominal value with an increasing sample size, while the rates for \(T_{\textrm{sub}}\) and \(T_{\beta }\) remained largely too conservative. For \(T_{\gamma }\) and \(T_{LR}\) , rejection rates were too liberal. In case of the log-normal distribution, \(T_{\textrm{sub}}\) and \(T_{\beta }\) yielded even higher type 1 error rates. Interestingly, while FRT-PI showed a good size for normally and t -distributed potential outcomes, the test was too liberal when the potential outcomes were log-normally distributed and when the samples size was small to moderate. In this case, the FRT-CI yielded more exact rejection rates. Finally, \(T_{V}\) \(T_{V}^{R}\) , \(T_{D}\) , and \(T_{D}^{R}\) were again near the nominal value, and the rates for \(T_{\textrm{sub}}\) and \(T_{\beta }\) were again largely unaffected by the sample size.

With regard to the power of the tests (see columns with \(\sigma _{\tau } = 0.25\) and \(\sigma _{\tau } = 0.50\) in Table 2 ), all tests were more powerful the larger the size of the effect and the larger the size of the two groups. However, there were notable differences between the tests depending on conditions. Specifically, \(T_{V}\) , \(T_{D}\) , \(T_{\gamma }\) , \(T_{LR}\) , and \(T_{\beta }\) were the most powerful tests in case of normally distributed data, irrespective of sample size and level of treatment effect variation. The rank-based FRT versions \(T_{V}^{R}\) and \(T_{D}^{R}\) were always less powerful than their raw-data counterparts \(T_{D}\) and \(T_{V}\) , respectively, and \(T_{\textrm{sub}}\) was more powerful than FRT-CI, but not FRT-PI. However, the latter three tests reached power rates above 80% only at 250 participants per group and when treatment effect variation was large. All other tests reached these values prior to these three tests when treatment effect variation was moderate and large, but even these tests did not reach a sufficient power for the small sample size condition. A similar result pattern occurred in conditions in which the potential outcomes were t -distributed. Again, \(T_{V}\) , \(T_{D}\) , \(T_{\gamma }\) , \(T_{LR}\) and \(T_{\beta }\) were the most powerful tests, although the result for \(T_{\gamma }\) and \(T_{LR}\) has to be considered in light of the large type 1 error rates when there was no effect variation. Interestingly, \(T_{\beta }\) , although also based on normal-theory, performed similar to \(T_{V}\) and \(T_{D}\) . Furthermore, and in contrast to the normal distribution condition, FRT-PI was more powerful than FRT-CI and \(T_{\textrm{sub}}\) and the rank-based versions of \(T_{V}\) and \(T_{D}\) had the same power rates as their raw-data counterparts. Finally, when the potential outcomes were log-normally distributed, \(T^{R}_{V}\) , \(T^{R}_{D}\) , \(T_{\gamma }\) , \(T_{LR}\) and FRT-PI were the most powerful tests. Again, for \(T_{\gamma }\) and \(T_{LR}\) this result has to be considered in light of the worse performance of the two tests in case of no treatment effect variation. Similarly, the results concerning the rank-based tests should be interpreted in comparison to their performance when the average treatment effect is one, where \(T^{R}_{V}\) and \(T^{R}_{D}\) yielded high rejection rates when the treatment effect was constant (see the discussion below).

The type 1 and type 2 error rates of the tests when considering an additional covariate were, unexpectedly, very similar to the error rates when not considering the covariate (see Table 3 for the specific results). When we examine the small sample size condition only (i.e., 25 participants per condition) and average across all tests, we find that for normally distributed data the mean rejection rate is 0.038 when \(\sigma _{\tau }\) is zero, it is .137 when \(\sigma _{\tau }\) is 0.25, and it is 0.331 when \(\sigma _{\tau }\) is 0.50. These values differ only slightly from the values that we obtain when we consider the tests without covariates, \(\sigma _{\tau }\) = 0: 0.038, \(\sigma _{\tau }\) = 0.25: .133, \(\sigma _{\tau }\) = 0.50: 0.333. Very similar results are obtained when we consider the conditions in which the data was t - or log-normal-distributed, and also when we consider each specific tests. Thus, in the conditions studied here, taking a covariate into account leads, if at all, only to a small improvement in the power of the tests, when the correlation between the covariate and the dependent variable does not exceed 0.3.

Finally, as mentioned above, the results are very similar for the conditions in which the average treatment effect is one (see Tables  6 and 7 in the Appendix for the specific error rates of the considered tests). Exceptions were the results for the rank tests \(T^{R}_{V}\) and \(T^{R}_{D}\) when the data were log-normally distributed. Here, rejection rates were unacceptably high when there was no treatment effect variation (i.e., \(\sigma _{\tau }\) = 0). To better understand these results, we conducted another small simulation study in which we examined the performance of a FRT when testing the null hypotheses that the average treatment effect is zero for log-normal data. The results showed (see Table 4 ) that the rank based test performed better than the raw-data based test when there was no treatment effect heterogeneity (i.e., \(\sigma _{\tau }\) = 0). However, when the treatment effect was zero, we found that rejection rates of the rank test increased the larger the variation in the treatment effect, while the raw-data based test had the correct size. This suggests that nonzero treatment effect heterogeneity results in a difference between the two outcome means in the rank data, which is actually not present, and this increases with higher heterogeneity. This ’bias’ also affects the rank-test of the variances (analogous to the test using the coefficient of variation, as discussed above). Finally, when the average treatment is one, then the actual difference in means is ’added’ to this bias, leading to the exceptional rejection rates.

Psychological researchers are increasingly interested in methods that allow them to detect whether a treatment effect investigated in a study is non-constant across participants. Based on the potential outcome framework, a number of procedures were suggested to test the null hypothesis of a homogeneous treatment effect. These tests can be distinguished according to whether they make distributional assumptions and to which sampling statistics are used in the test. The present study was done to examine the type 1 and type 2 error rates of the suggested tests as a function of the amount of treatment heterogeneity, the presence of an average causal effect, the distribution of the potential outcomes, the sample size, and of whether a covariate is considered when conducting the test.

With regard to the type 1 error rate, our results replicate the findings of earlier simulation research (Bloome & Schrage, 2021 ; Ding et al., 2016 ) by showing that the majority of tests were close to the nominal \(\alpha \) -level regardless of sample size when the data was normally distributed. However, extending prior research we also found that the variance tests in the heterogeneous regression model \(T_{\gamma }\) and the LR test implemented with a multiple group structural equation model \(T_{LR}\) rejected the null hypothesis too often in the case of non-normally distributed data. Furthermore, we found that the subsampling procedure \(T_{sub}\) and the test in the random coefficient regression model \(T_{\beta }\) decided too conservatively in these conditions, and that the FRT-CI performed best in case of skewed data. Overall, these results suggest that, regardless of sample size, applied researchers should use a Fisher randomization test with variance ratios or variance differences (i.e., \(T_{V}\) , \(T_{D}\) ) or the empirical distribution function (i.e., FRT-CI), because they protect well against false positive decisions. When the data are normally distributed, they could, again regardless of sample size, use the variance tests in the heterogeneous regression model \(T_{\gamma }\) and the LR test, but should use one of the FRT tests as a sensitivity check if there is any doubt as to whether the normality assumption is met.

Concerning the power of the tests, the results of the simulation – at least for the small sample sizes of 25 and 50 persons per group – are quite sobering, because none of the tests reached satisfactory power levels even when size of treatment heterogeneity was stronger. When samples sizes were larger, our results were consistent with earlier research showing that the variance test of the heterogeneous regression model is characterized by good type 2 error rates in case of normally distributed data (Bloome & Schrage, 2021 ). They also show that the LR-test and the test of the random coefficient regression model achieved good power. Power rates of all three tests were slightly larger than the power rates of the variance ratio and the variance difference tests, but this is to be expected given that the parametric assumptions are met in these conditions. Furthermore, the power of FRT-PI increased with larger sample sizes and with larger treatment effect heterogeneity. The same pattern occurred for FRT-CI, although it performed better (in terms of type 2 and type 1 error rates) than FRT-PI in case of skewed data. For practitioners these results suggest that they should use the FRT variance tests, the variance test in the heterogeneous regression model \(T_{\gamma }\) or the LR test when the data is normally distributed. However, they should keep in mind that the power is only acceptable for sample sizes greater than or equal to 50 participants per group in case of large heterogeneity in treatment effects, or with 250 participants per group in case of moderate heterogeneity. In the case of non-normally distributed data, they should use the FRT variance tests or the FRT-PI test. Once again, however, when interpreting the result, it is important to bear in mind that the power is only sufficiently high for very large samples (250 people per group in case of high heterogeneity).

We also examined the performance of rank-based versions of the variance ratio and the variance difference tests, because in the case of the average treatment effect, simulation studies show that an FRT that uses rank data (i.e., the initial data is transformed into ranks in a first step) performs well across many simulation conditions (Imbens & Rubin, 2015 ; Rosenbaum, 2002 , 2010 ). In our simulations, these tests performed similar (in case of t -distributed data) or worse (in case of normally distributed data) than their raw-data based counterparts. Furthermore, in the case of log-normal distributed data, their performance was unsatisfactory. Thus, we provisionally conclude that the performance advantage that is observed for the average treatment effect does not generalize to the detection of a heterogeneous treatment effect. However, our results have to be replicated in future simulation studies to reach a final conclusion.

Finally, we also investigated whether the power of the tests is increased by considering a relevant covariate. However, our results show only a tiny effect of including a covariate. The obvious explanation is that the influence of the covariate was too small in our simulation to detect an effect on power. We used a moderate effect, because we think this is the most plausible value for the considered setting in which participants are randomly assigned to treatment. Nevertheless, future research should replicate and also extend our results by additionally examining larger sizes of the covariate’s effect. Another point to consider is that covariates are often not measured with perfect reliability, which in turn may also affect the error rates of the tests for treatment effect heterogeneity. In fact, we assumed here that the outcome variable is not subject to measurement error and it remains unclear how a violation of this assumption would affect the different tests. We think that this is also an interesting question to examine in future research.

Furthermore, in our simulation study, we focused on tests that have been proposed in the causal inference literature to test for treatment effect heterogeneity. However, in the context of methods that compare variance terms, the statistical literature suggests a number of further tests that are aimed to be more robust to violations of the normal distribution, such as the Levene test or the Brown and Forsythe test (see Wilcox, 2017b , for an overview) or tests that are based on bootstrapping (see Lim & Loh, 1996 ; Wilcox, 2017a ). We expect these tests to perform similarly to the FRT tests, though this assumption should be validated in a future simulation study. Finally, in the case of the average treatment effect, previous research has found that the meta-analytical integration of the results of many small-sample studies can match a single, large-sample study in terms of power (e.g., Cappelleri et al., 1996 ). This suggests that the pooled results of several heterogeneous treatment effect tests may have a sufficient power, even when the single studies are underpowered due to using small samples. We think that testing this hypothesis in future research is not only interesting from an applied perspective, but also from a methodological point of view: Although meta-analytic methods for the variance ratio statistic exist (see Nakagawa et al., 2015 ; Senior et al., 2020 )), it is currently unclear, at least to our knowledge, how to best pool the results of the FRT tests or the quantile tests (i.e., whether Fisher’s or Stouffer’s method is appropriate, for example, when there is substantial between-study heterogeneity). Footnote 4

To summarize, our results suggest that researchers often fail to reject the null hypothesis of a constant treatment effect in a single study even when there is actual heterogeneity in effects present in the data. We think that this result is relevant for applied researchers from multiple points of view. To begin with, currently the sample sizes are determined a priori in such a way that a pre-specified average (causal) effect can be tested with as much power as possible. Thus, assuming that future studies will extend their focus to treatment effect heterogeneity, much larger samples sizes have to be assessed, at least when the variables that are responsible for treatment effect heterogeneity are not known before conducting the RCT.

Specifically, in our study we examined the setting that researchers have not assessed or do not know the heterogeneity-generating variables and therefore perform one of the (global) tests considered here. However, researchers may sometimes know these variables prior to the randomization and may then, assuming that they have assessed them and that a linear model is true, compute a regression model with an interaction term to test whether the treatment effect varies with this variable. In this case, the power of the interaction test is larger than the power of the tests considered in the simulation. For instance, when the population model is linear and the interaction term has a moderate effect ( \(R^2\) about .13), the power of the interaction test is higher than the power of the variance ratio and the variance difference tests (see Table 5 ). Footnote 5 For applied researchers this result suggests, second, that they should already consider which variables can explain potential variation in the average treatment effect during the planning stage of the study, because in this case a much higher power can be achieved at lower samples sizes.

A final recommendation for applied researchers pertains to the case that one of the tests studied here leads to the rejection of the null hypothesis of a constant treatment effect. Then, researchers will be motivated to detect the person-level variables that explain differences in the treatment effect. In the introduction we mentioned that there are a number of statistical approaches available (classical as well as more modern approaches from machine learning) that can then be used for this task. When performing these (post-hoc) analyses, however, it has to be taken into account that one potentially conducts a large number of statistical tests, which may lead to many false-positive results (Schulz and Grimes, 2005 ; Sun et al., 2014 ). Thus, one has to investigate in other studies how stable (in terms of replicability) and generalizable (in terms of external validity) the resulting findings are, also given that the sample sizes are (typically) optimized with respect to the statistical test of the average treatment effect.

To conclude, we conducted a simulation study to investigate the type 1 and type 2 error rates of different tests of treatment effect heterogeneity that were suggested in the causal inference literature. The results suggest that a randomization test should be used in order to have good control of the type 1 error. Furthermore, all tests studied are associated with high type 2 error rates when sample sizes are small to moderate. Thus, to detect heterogeneous treatment effects with sufficient power, much larger samples are needed than those typically collected in current studies, or new test procedures must be developed that have higher power even with smaller samples.

We also computed \(T_{CV}\) in selected conditions of our simulation. When the average treatment effect and the variance of the treatment effects was 0, the rejection rate of \(T_{CV}\) was near the nominal value (i.e., 0.05). However, when the average treatment effect was 1, but the variance of the treatment effects was 0, the rejection rate was 0.935.

The heterogeneous regression model, the random coefficient model, and the structural equation model assume a linear relationship between the covariates and the outcome. When this assumption is suspected to be violated, one could also first predict the outcome with the covariates using any machine learning model and then proceed with the residuals from this model.

Chernozhukov and Fernandez ( 2005 ) also suggest a bootstrap-variant of their approach that we also included in the simulation. However, the performance of the test with regard to the type 1 and type 2 error rates was unsatisfactory (see Ding et al., 2016 , for similar findings), so that we decided to not report results concerning this test.

In a preliminary simulation study, we examined the power of a pooled variance ratio test depending on the size of treatment effect heterogeneity in the single studies, the number of the studies to be pooled, and the amount of between-study heterogeneity. Specifically, to generate the data for a single study, we used the same population model as in the simulation study reported in the main text. The differences were that we generated data for a small, a moderate, and a large heterogeneous treatment effect (i.e., the standard deviation of \(\sigma _{\tau }\) was set to 0.10, 0.25, or 0.50; see Eq. 21 ), and that we considered the small sample size condition only (i.e., 25 persons in the experimental and the control group in a single study). In addition, we varied the amount of systematic variation of the heterogeneous treatment effect across studies (i.e., the between-study heterogeneity was either 0 or 0.10) and we varied the number of studies that are meta-analytically integrated (i.e., 10 vs. 30 vs. 50 studies). In each of the 1000 replications generated for a simulation condition, we computed a random-effect meta-analysis (using the metafor package, see Viechtbauer, 2010 ) and checked whether the pooled variance ratio was significantly different from zero. The results showed that when the size of the heterogeneous treatment effect was small, the power of the pooled test was adequate, when the number of aggregated studies was 50 and when there was no between-study heterogeneity (i.e., the power was .816). When between-study heterogeneity was 0.10, the power was lower than .80 when the number of to-be-aggregated studies was 50 (i.e., the power was .746). Furthermore, when the heterogeneous treatment effect was moderate or large, the power of the pooled variance ratio test was already adequate when the number of studies was 10 (i.e., the power was near 1.00 in almost all conditions), independent upon the amount of between-study heterogeneity. The exception was the moderate heterogeneous treatment effect condition in which between-study heterogeneity was 0.10; here, the nominal power level was not reached (i.e., the power was .750). However, we note that these results were obtained under rather optimal conditions (i.e., correct test statistic; distributional assumptions are met) and that they have to be replicated in future simulation research.

The model used to generate the data was

were A is the treatment variable (with prevalence 0.5) and X is a standard normal variable. The residual terms were also standard normally distributed.

Athey, S., Wager, S., & Tibshirani, J. (2019). Generalized random forests. Annals of Statistics, 47 , 1148–1178. https://doi.org/10.1214/18-AOS1709

Article   MathSciNet   Google Scholar  

Bloome, D., & Schrage, D. (2021). Covariance regression models for studying treatment effect heterogeneity across one or more outcomes: Understanding how treatments shape inequality. Sociological Methods & Research, 50 , 1034–1072. https://doi.org/10.1177/0049124119882449

Bollen, K. A. (1989). Structural equations with latent variables . West Sussex: John Wiley & Sons.

Book   Google Scholar  

Cappelleri, J. C., & loannidis, J.P.A., Schmid, C.H., de Ferranti, S.D., Aubert, M., Chalmers, T.C., Lau, J. (1996). Large trials vs meta-analysis of smaller trials: How do their results compare? JAMA, 276 , 1332–1338. https://doi.org/10.1001/jama.1996.03540160054033

Casella, G., & Berger, R. L. (2002). Statistical inference . Duxbury Press.

Google Scholar  

Chernozhukov, V., & Fernandez-Val, I. (2005). Subsampling inference on quantile regression processes. Sankhya: The Indian Journal of Statistics, 67 , 253–276.

MathSciNet   Google Scholar  

Cook, T. D. (2018). Twenty-six assumptions that have to be met if single random assignment experiments are to warrant ‘gold standard’ status: A commentary on deaton and cartwright. Social science & medicine, 210 , 37–40. https://doi.org/10.1016/j.socscimed.2018.04.031

Article   Google Scholar  

Cox, D. R. (1984). Interaction. International Statistics Review, 52 , 1–24. https://doi.org/10.2307/1403235

Deaton, A., & Cartwright, N. (2018). Understanding and misunderstanding randomized controlled trials. Social Science & Medicine, 210 , 2–21. https://doi.org/10.1016/j.socscimed.2017.12.005

Ding, P., Feller, A., & Miratrix, L. (2016). Randomization inference for treatment effect variation. Journal of the Royal Statistical Society, Section B, 78 , 655–671.

Giner, G., & Smyth, G. K. (2016). statmod: Probability calculations for the inverse gaussian distribution. R Journal, 8 , 339–351.

Hallquist, M. N., & Wiley, J. F. (2018). MplusAutomation: An R package for facilitating large-scale latent variable analyses in Mplus. Structural Equation Modeling, 621–638 ,. https://doi.org/10.1080/10705511.2017.1402334

Hao, L., & Naiman, D. Q. (2007). Quantile regression . Thousand Oaks, California: Sage.

Hernan, M., & Robins, J. M. (2020). Causal inference: What if . Boca Raton: Chapman & Hall/CRC.

Hildreth, C., & Houck, J. P. (1968). Some estimators for a linear model with random coefficients. Journal of the American Statistical Association, 63 , 584–595. https://doi.org/10.2307/2284029

Holland, P. W. (1986). Statistics and causal inference. Journal of the American Statistical Association, 81 , 945–960. https://doi.org/10.2307/2289064

Imbens, G. W., & Rubin, D. (2015). Causal inference for statistics, social, and biomedical sciences: An introduction . Cambridge: Cambridge University Press.

Kaiser, T., Volkmann, C., Volkmann, A., Karyotaki, E., Cuijpers, P., & Brakemeier, E.- L. (2022). Heterogeneity of treatment effects in trials on psychotherapy of depression. Clinical Psychology: Science and Practice. https://doi.org/10.1037/cps0000079

Koenker, R., & Xiao, Z. (2002). Inference on the quantile regression process. Econometrica, 70 , 1583–1612. https://doi.org/10.1111/1468-0262.00342

Kravitz, R. L., Duan, N., & Braslow, J. (2004). Evidence-based medicine, heterogeneity of treatment effects, and the trouble with averages. The Milbank quarterly, 82 , 661–687. https://doi.org/10.1111/j.0887-378X.2004.00327.x

Article   PubMed   PubMed Central   Google Scholar  

Künzel, S. R., Sekhon, J. S., Bickel, P. J., & Yu, B. (2019). Metalearners for estimating heterogeneous treatment effects using machine learning. Proceedings of the National Academy of Science, 116 , 4156–4165. https://doi.org/10.1073/pnas.1804597116

Article   CAS   Google Scholar  

Lim, T.- S., & Loh, W.- Y. (1996). A comparison of tests of equality of variances. Computational Statistics & Data Analysis, 22 , 287–301. https://doi.org/10.1016/0167-9473(95)00054-2

Murnane, R. J., & Willett, J. B. (2011). Methods matter: Improving causal inference in educational and social science research . Oxford: Oxford University Press.

Muthén, B. O., Muthén, L. K., & Asparouhov, T. (2017). Regression and mediation analyses using mplus . Los Angeles: Muthén & Muthén.

Muthén, B. O., Muthén, L. K., & Asparouhov, T. (2017). Regression and mediation analyses using mplus . Los Angeles, CA: Muthén & Muthén.

Nakagawa, S., Poulin, R., Mengersen, K., Reinhold, K., Engqvist, L., Lagisz, M., & Senior, A. M. (2015). Meta-analysis of variation: Ecological and evolutionary applications and beyond. Methods in Ecology and Evolution, 6 , 143–152. https://doi.org/10.1111/2041-210X.12309

Powers, S., Qian, J., K.J., et al. (2018). Some methods for heterogeneous treatment effect estimation in high dimensions. Statistics in Medicine, 37 , 1767–1787. https://doi.org/10.1002/sim.7623

Rosenbaum, P. R. (2002). Observational studies . New York: Springer.

Rosenbaum, P. R. (2010). Design of observational studies . New York: Springer.

Rosseel, Y. (2012). Lavaan: An R package for structural equation modeling. Journal of Statistical Software, 48 , 1–36. https://doi.org/10.18637/jss.v048.i02

Salditt, M., Eckes, T., & Nestler, S. (2023). A tutorial introduction to heterogeneous treatment effect estimation with meta-learners. Administration and Policy in Mental Health and Mental Health Services Research . https://doi.org/10.1007/s10488-023-01303-9

Article   PubMed   Google Scholar  

Schulz, K. F., & Grimes, D. A. (2005). Multiplicity in randomised trials ii: subgroup and interim analyses. The Lancet, 365 , 1657–1661. https://doi.org/10.1016/S0140-6736(05)66516-6

Senior, A. M., Viechtbauer, W., & Nakagawa, S. (2020). Revisiting and expanding the meta-analysis of variation: The log coefficient of variation ratio. Research Synthesis Methods, 11 , 553–567. https://doi.org/10.1002/jrsm.1423

Sun, X., Ioannidis, J. P., Agoritsas, T., Alba, A. C., & Guyatt, G. (2014). How to use a subgroup analysis: Users’ guide to the medical literature. Jama, 311 , 405–411. https://doi.org/10.1001/jama.2013.285063

Article   CAS   PubMed   Google Scholar  

Tucker-Drob, E. M. (2011). Individual difference methods for randomized experiments. Psychological Methods, 16 , 298–318. https://doi.org/10.1037/a0023349

Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software , 36 (3), 1–48. https://doi.org/10.18637/jss.v036.i03

Volkmann, C., Volkmann, A., & Müller, C. A. (2020). On the treatment effect heterogeneity of antidepressants in major depression: A bayesian meta-analysis and simulation study. Plos One, 15 , e0241497. https://doi.org/10.1371/journal.pone.0241497

Article   CAS   PubMed   PubMed Central   Google Scholar  

Wasserman, L. (2004). All of statistics . New York: Springer.

Wendling, T., Jung, K., Callahan, A., Schuler, A., Shah, N. H., & Gallego, B. (2018). Comparing methods for estimation of heterogeneous treatment effects using observational data from health care databases. Statistics in Medicine, 37 , 3309–3324. https://doi.org/10.1002/sim.7820

Western, B., & Bloome, D. (2009). Variance function regressions for studying inequality. Sociological Methodology, 39 , 293–326. https://doi.org/10.1111/j.1467-9531.2009.0122

Wilcox, R. R. (2017). Introduction to robust estimation and hypothesis testing . West Sussex: John Wiley & Sons.

Wilcox, R. R. (2017). Understanding and applying basic statistical methods using R . West Sussex: John Wiley & Sons.

Download references

Open Access funding enabled and organized by Projekt DEAL.

Author information

Authors and affiliations.

University of Münster, Institut für Psychologie, Fliednerstr. 21, 48149, Münster, Germany

Steffen Nestler & Marie Salditt

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Steffen Nestler .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Additional materials for this article can be found at https://osf.io/nbrg2/ . The materials on the OSF include the R code for the simulation study and the Mplus code to estimate the random coefficient regression model.

Additional results

Here, we present additional results of the simulation study. Table 6 displays the results for the examined tests when no cova-riates are considered and when the average treatment effect is 1, and Table 7 shows the results for the tests with covariates considered and for an average treatment effect of 1.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Nestler, S., Salditt, M. Comparing type 1 and type 2 error rates of different tests for heterogeneous treatment effects. Behav Res (2024). https://doi.org/10.3758/s13428-024-02371-x

Download citation

Accepted : 13 February 2024

Published : 20 March 2024

DOI : https://doi.org/10.3758/s13428-024-02371-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Heterogeneous treatment effects
• Randomization tests
• Heterogeneous regression
• Find a journal
• Publish with us
• Track your research