2d and 3d shapes problem solving

Spatial reasoning skills about 2D representations of 3D geometrical shapes in grades 4 to 9

• Original Article
• Open access
• Published: 27 May 2020
• Volume 32 , pages 235–255, ( 2020 )

Cite this article

You have full access to this open access article

• Taro Fujita   ORCID: orcid.org/0000-0002-3547-456X 1 ,
• Yutaka Kondo 2 ,
• Hiroyuki Kumakura 3 ,
• Susumu Kunimune 3 &
• Keith Jones   ORCID: orcid.org/0000-0003-3677-8802 4  

13k Accesses

20 Citations

5 Altmetric

Explore all metrics

Given the important role played by students’ spatial reasoning skills, in this paper we analyse how students use these skills to solve problems involving 2D representations of 3D geometrical shapes. Using data from in total 1357 grades 4 to 9 students, we examine how they visualise shapes in the given diagrams and make use of properties of shapes to reason. We found that using either spatial visualisation or property-based spatial analytic reasoning is not enough for the problems that required more than one step of reasoning, but also that these two skills have to be harmonised by domain-specific knowledge in order to overcome the perceptual appearance (or “look”) of the given diagram. We argue that more opportunities might be given to both primary and secondary school students in which they can exercise not only their spatial reasoning skills but also consolidate and use their existing domain-specific knowledge of geometry for productive reasoning in geometry.

Similar content being viewed by others

Analyzing the Relation Between Spatial and Geometric Reasoning for Elementary and Middle School Students

On the multitude of mathematics skills: spatial-numerical associations and geometry skill.

Geometry and Visual Reasoning

Avoid common mistakes on your manuscript.

Introduction

In a recent research review, Jones and Tzekaki ( 2016 ) summarise how research is focussing on “the development of students’ knowledge regarding understanding of geometric figure, definitions and inclusion relations, identification of shapes and language issues” (p. 109). In this, geometrical reasoning is a vital component in students’ tackling of problems involving geometrical figures. In geometry, figures are often in the form of diagrams (on paper or computer screen) and working with such representations (including geometric figures imagined by students) is important during geometric reasoning (Lowrie 2012 ; Fujita et al. 2017 ). When working with problems involving 2D representations of 3D shapes, students use various skills to solve the problems. Mulligan et al. ( 2018 ) say that an “integrated definition of spatial reasoning” includes the skills related to mental manipulations of visual stimuli, transforming spatial forms into other visual forms with analytical thinking of structural features of spatial forms (p. 78). At the same time, research studies also suggest that spatial skills such as manipulating given representations and reasoning can be improved through certain training or interventions (e.g. Fischbein 1993 , p. 156; Lowrie et al. 2019 ).

Our goal is to identify students’ spatial reasoning skills, and how they use their skills and knowledge to solve geometrical problems, in order to design interventions to improve teaching. In this paper, we particularly focus on the following two research questions:

RQ1: How do students across the grades use their spatial reasoning skills and domain-specific knowledge when tackling problems involving 3D geometrical shapes represented in 2D?

RQ2: What can be learnt from students’ use of such skills and knowledge in order to design and implement future interventions to improve their skills and knowledge?

We pose these questions because we speculate students’ use of spatial reasoning skills might be related to their domain-specific knowledge around elements, properties and concepts of geometrical figures (see next section). We study students from across the grades from primary to secondary because in mathematics education research not so much has been reported about students’ reasoning with 3D shapes across primary and secondary schools. More research studies are needed, not only of the teaching and learning of 3D geometry in primary schools (Sinclair and Bruce 2015 ; Sinclair et al. 2016 ) but also across primary to secondary schools to obtain a more comprehensive picture of the development of students’ understanding. In particular, if common patterns in student skills and difficulties can be identified, then such information is likely to be useful for designing effective teaching interventions for improving students’ spatial skills.

In what follows, we first construct our theoretical framework to consider the relationships between, and student use of, spatial reasoning skills and domain-specific knowledge of geometry. We then report findings from our survey of 1357 students from grades 4–9 in Japan and our observations of students’ thinking in a classroom-based study with a lesson based on a sample of tasks used in the survey. We then discuss what implications can be gained from our study which we believe to be useful for designing effective teaching interventions for improving students’ spatial skills and knowledge. Finally, we suggest some ideas for such teaching interventions.

Theoretical framework

Spatial reasoning skills in 3d geometry problem solving with 2d representations.

Pittalis and Christou ( 2010 ) identified four types of reasoning with 3D geometry: the representation of 3D objects, spatial structuring, conceptualisation of mathematical properties and measurement. These four types of reasoning are closely related to more general spatial skills such as spatial visualisation, orientation (e.g. remaining unconfused by changing orientations) or relations (e.g. mentally rotating objects) (p. 195). Lowrie et al. ( 2018 ) also list mental rotation, spatial orientation and spatial visualisation as spatial reasoning skills. In this paper, we particularly focus on the skills related to manipulating internal/external representations of 3D shapes and reasoning with geometric properties, because geometrical reasoning is characterised by the interaction between these two aspects, the visual (figural) and the conceptual (Duval 2017 , p. 63).

Fischbein ( 1993 ) proposed the notion of “figural concept” such that, while a geometrical figure (such as a square) can be described as having intrinsic conceptual properties (in that it is controlled by geometrical theory), a geometrical figure is not solely a concept but rather an image too (ibid, p. 141). Various representations of geometrical shapes, such as diagrams, are used in geometry problems so that problem solving often involves encoding information from these representations (Lowrie 2012 , p. 151). In a study of students working with 3D geometric shapes, Pittalis and Christou ( 2013 , p. 676) identified the skills of coding information, e.g. manipulating and constructing nets, constructing 2D drawings of 3D shapes, and translating from one representation mode to another and decoding information, e.g. interpreting structural elements of representations of 3D shapes and geometrical properties. Battista et al. ( 2018 , p. 195) also propose coding/decoding skills, taking spatial visualisation as “mentally creating and manipulating images of objects in space, from fixed or changing perspectives on the objects, so that one can reason about the objects and actions on them, both when the objects are and are not visible” and refer to property-based spatial analytic reasoning (“decomposes objects into their parts using geometric properties to specify how the parts or shapes are related, and, using these relationships, operates on the parts”).

Based on the above, in this paper we take the following two skills as core spatial reasoning skills for problem solving with 3D geometrical shapes represented in 2D:

Spatial visualisation (coding) : mental manipulations of visual images of shapes including rotating, transforming the given diagrams to another form, reorienting, drawing nets and adding additional lines.

Property-based spatial analytic reasoning (decoding) : interpreting the structural elements of shapes and decomposing objects into their parts using geometric properties for reasoning and decision-making

Use of spatial reasoning skills and domain-specific knowledge

In geometry, it is known that certain images of geometrical shapes can disturb students’ geometrical reasoning. A well-known example is the effect of prototypical images such as ‘slanted’ images for parallelograms in that through such images students do not include rectangles or squares as special cases of parallelograms even if they can state an appropriate definition of a parallelogram (e.g. Fujita 2012 ). Aspinwall et al. ( 1997 ) conceptualized the limitation of the use of visual imaginary as an uncontrollable image , described as “preventing the opening up of more fruitful avenues of thought, a difficulty which is particularly acute if the image is vivid” (p. 301). Another example is the dual process in which errors are “the result of either an uncontrolled intuitive thought process (no conflict-detection) or an unsuccessful intervention of the analytical processing system” (Van Hoof et al. 2013 , p. 155, see also Gillard et al. 2009 ).

Llinares and Clemente ( 2019 ) refer to configural reasoning , which coordinates visual/figural and conceptual aspects of geometrical shapes. In this paper, we consider that students’ statement around elements, properties and concepts of geometrical figures, i.e. domain-specific knowledge (Chinnappan et al. 2012 ) might also be important for coordinating visual and conceptual aspects in addition to general spatial reasoning skills described in the previous section. For example, Ufer et al. ( 2008 ) studied procedural knowledge (e.g. simple calculations in geometry) and declarative knowledge (e.g. recalling basic definitions, theorems, and concepts) and problem solving skills. They identified declarative knowledge to be the strongest influence on successful proving in geometry, with such knowledge being in the form “A is B”, “in X, A is B”, etc., in students’ discursive expression. In this paper, we take students’ statement around elements, properties and concepts of geometrical figures as “domain-specific knowledge” of geometrical shapes. Their property-based spatial analytic reasoning is represented by the use of knowledge, often accompanying by verbal or written explanations that use the word “because”. Whether correct knowledge or not, in principle domain-specific knowledge in geometry (i.e. the concepts, principles and conventions unique to that domain and represented by in X, A is B, such as “In a cube, all faces are squares”) plays a kind of coordinating role between spatial visualisation and property-based spatial analytic reasoning (of course, if students have incorrect knowledge about shapes then this can lead to incorrect answers).

Types of answers in 3D geometry problem solving

In 3D geometry, the use of spatial reasoning skills and domain-specific knowledge can lead both to successful and unsuccessful problem solving. In our previous studies (Fujita et al. 2017 ), by using data from 455 grades 7–9 students, geometric reasoning with 3D shapes were classified into five types in terms of mental manipulations of figures and reasoning based on geometric properties. In this paper, we also use the categories to see students’ use of spatial reasoning skills and domain-specific knowledge in more integrated ways, described as follows:

Type 1: Incorrect answer led by two-dimensional or intuitive global judgments without any explicit use of spatial visualisation and property-based spatial analytic reasoning ;

Type 2A: Incorrect answer only led by property-based spatial analytic reasoning but with logical gaps or influenced by visual information and/or incorrect/inappropriate domain-specific knowledge ;

Type 2B: Incorrect answer with only spatial visualisations but influenced by visual information and/or incorrect/inappropriate domain-specific knowledge ;

Type 2C: Incorrect answer with the use of spatial visualisation and property-based spatial analytic reasoning but influenced by visual information and/or incorrect/inappropriate domain-specific knowledge ;

Type 3: correct answer with valid use of spatial visualisation and/or property-based spatial analytic reasoning with correct domain-specific knowledge

This classification enables us to identify what makes students’ problems solving successful/unsuccessful in their use of spatial reasoning skills and domain-specific knowledge , represented by various forms (e.g. verbal, written) of students’ answers. For example, suppose a student answered “AB=CD” for Q2-(2) (Fig.  1 ). Then, this student answered AB=CD because of the use of incorrect knowledge “in a cube all sides and edges have the same length” (type 2B). If a student has knowledge that ‘in a cube, diagonals of each face are equal’, then they might be able to reason triangle ABC in Fig. 1 question Q3-(2) is equilateral, despite it does not look like an equilateral triangle in the given diagram (type 3). Another student might reason “CA=CB because they are diagonal” and conclude it is an isosceles triangle but no further manipulations are used (type 2A), mentally rotate the given diagram and then conclude isosceles, but not stating domain-specific knowledge explicitly to reason why (type 2B), or mentally extract triangles but no manipulations for the side AB and used “CA = CB because they are diagonal” but conclude it is isosceles (type 2C). Also, knowledge about isosceles triangle is “inappropriate” in this problem context as its use is unlikely to lead to a correct answer.

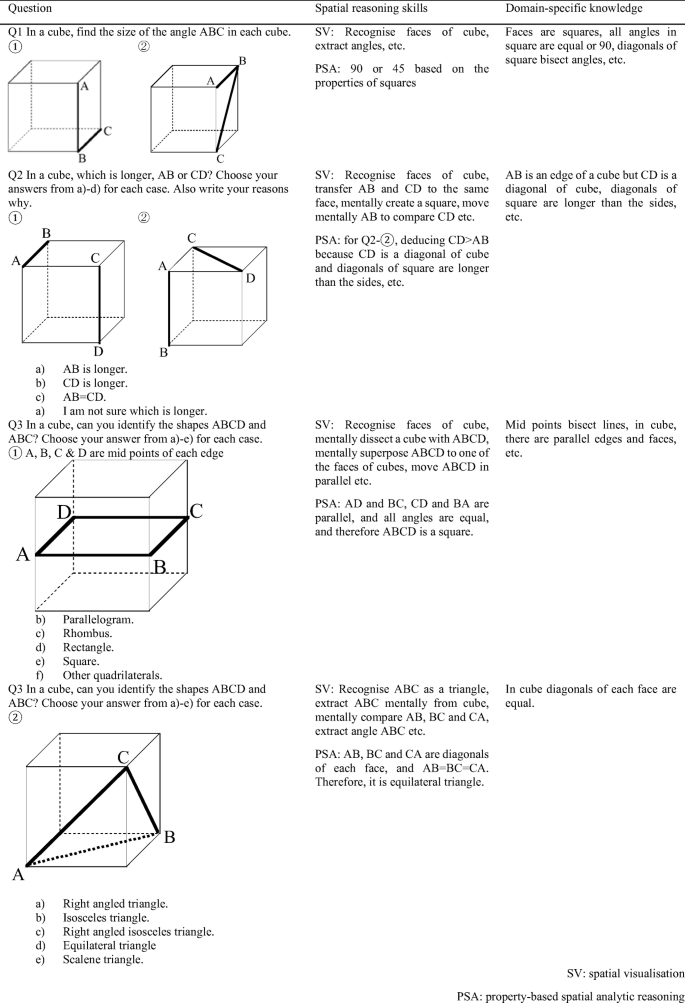
Question items for primary and lower secondary schools

Methodology

By selecting students in Japan, we were aware that the students would have had various learning experiences involving basic knowledge about 3D shapes including cubes, cuboids, prisms, pyramids, nets and how to represent 3D shapes in 2D, by following the Japanese curriculum:

In primary schools, cube and cuboid are introduced in G4, and then in G5, they further learn prisms, cylinder, nets and 2D representations of 3D shapes. Also by G4, they have learnt different triangles (equilateral, isosceles, scalene, right angled, etc.), quadrilaterals (square, rectangle, rhombus, parallelogram), parallel/perpendicular lines, angles, diagonals of quadrilaterals, etc. Although deductive proofs are not studied, students are encouraged to explain their reasoning with practical activities in mathematics lessons;

In secondary schools, G7, students study geometrical constructions, symmetry and selected properties of solid figures (names of 3D shapes, nets, surface areas and volume) informally, but logically, to establish the basis of the learning of proof which is introduced in G8 in a context of congruent triangles. In G9, students learn similar figures and properties of circles, drawing on their consolidated capacity to use proof in geometry and Pythagorean Theorem with both 2D and 3D shapes.

In order to answer RQ1, a survey was conducted with 261 grade (G)4, 213 G5, 209 G6, 225 G7, 224 G8 and 225 G9 students (in total 1357 grades 4–9 students aged from 10 to 15 years old) from state Japanese primary and lower secondary schools. The survey items do not appear in Japanese textbooks and we consider that, in using these, we would be able to identify “geometric thinking beyond that which is typically elicited in conventional lessons” (Fujita et al. 2017 , p. 100). Q1–3 were answered by all the students. For each item, oblique parallel projections of cubes (as in Figs.  1 and 2 ) were used as such representations would be familiar to students (Kondo et al. 2014 ; see, also, Parzysz 1991 ). They were designed using cubes, because (a) it is a familiar shape for students and also (b) it is possible to include mathematically challenging problems which can help reveal students’ use of spatial reasoning skills , and domain-specific knowledge . Expected use of spatial reasoning skills , and domain-specific knowledge , through our a priori analysis, are summarised in Figs. 1 and 2 (note for some question, one of spatial reasoning skills might be enough to answer a question correctly, e.g. Q3-(1), Q4 etc.). Also, for each question, duplicating knowledge is omitted; e.g. for Q5 “In a cube, the diagonals of each face are equal” might be used). Based on our previous studies and theoretical framework, students across G4–6 might find Q2-(2) or Q3-(2) to be difficult as they need to control their spatial reasoning skills by using domain-specific knowledge , and similarly across G7–9 for Q5, resulting more type 2A-2C answers to these questions.

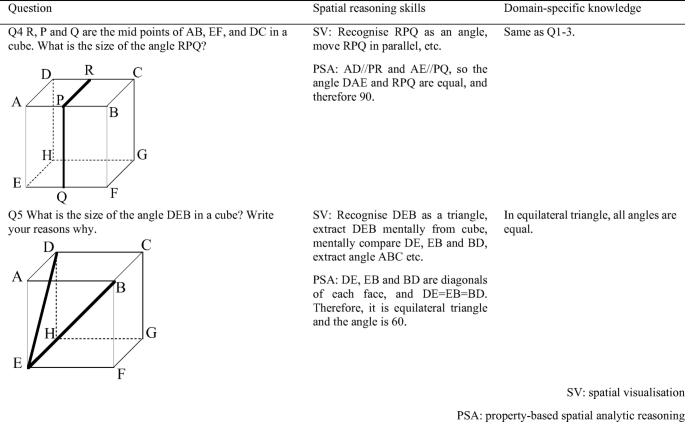
Additional question items for lower secondary schools

While the survey provides an overall account of the students’ use of spatial reasoning skills and knowledge with 3D shapes (characterised through the survey questions with cubes), it has certain limitations. In particular, from the survey, we could only judge the types of the answers from “written” responses, which might influence students’ thinking processes. Also, some students might not be familiar with writing their reasoning in a test situation. We are aware of these limitations in our study, but we believe we managed to extract useful information on students’ use of spatial reasoning skills and domain-specific knowledge from the survey, as shown in our results section.

Lesson observation

In order to gain further information which might have influenced our survey data, in particular students’ thinking processes, we also conducted a classroom-based study in which G6 students undertook Q5. We are aware that Q5 was probably too difficult for such students but, as an exploratory stage in lesson implementation, we wanted to see how the G6 students would tackle Q5.

A 45-min lesson was implemented in February 2019 by Mr. T with more than 20 years of teaching experience. Also the lesson was planned with the authors. The 34 students undertook the pre-/post-survey (using the tasks shown in Figs. 1 and 2 ) in December 2018 and March 2019 respectively. The first four authors observed the lesson and undertook their notes individually, video-recoded some of individual/group work and then these notes were shared in the post-lesson discussion and analysis. We focus on a student (SW) and examine her learning processes by describing the use of spatial reasoning skills and domain-specific knowledge in terms of the types of answers during the lesson. Student SW was randomly chosen by two of the observers at the beginning of the lesson ad hoc, and we recorded her thinking processes in lesson observation notes and video clips (a standard method of lesson observation data collection in Japan).

Data analysis

We first identified groups of geometry problems with similar difficulty levels. We created a 1357 × 6 matrix for both primary and secondary schools and a 674 × 8 matrix for secondary schools’ results with two variables (not correct, correct), and conducted an analysis using the Item Response theory approach (Sijtsma and Molenaar 2002 ) with R 3.3.3 with the packages “ltm” and “irtoys”. We undertook 2-parameter logistic (2PL) model analysis with the following two parameters: difficulties and discriminations. We use the 2PL model because the model is appropriate to see overall relationships of items in terms of the difficulties of each item (the difficulties parameter), and differences between students at different grade levels (the discrimination parameter).

Once we gained an overall picture of the students’ responses, we then examine the students’ written explanations in the survey further as such explanations represent evidence of what spatial reasoning skills and domain-specific knowledge which students were using to try and solve the geometric problems (this addresses RQ1). For the primary school students’ responses, we paid particular attention to Q2 (for which G4–9 students were asked to write their explanation) and Q5 (for which G7–9 were asked to write their explanation). In analysing the written responses to Q2-(2) and Q5, we use the types of answers to account for students’ use of spatial reasoning skills and domain-specific knowledge as well as in what ways some students had difficulties reaching correct answers for the given problems. Informed by our a priori analysis shown in Figs. 1 and 2 , we first coded selected sampled examples individually, compared our preliminary coding, and continued our discussion until we agreed. We also did lesson observations together, and have had more than 5 h of face-to-face discussions to agree how to code examples from the lessons. After this, we divided data into three sets and three of the authors completed the coding for Q2-(2) and Q5. The examples from student SW were coded by two authors independently, and no major disagreements were found. Then the analysis was shared with the other authors and agreed. Finally, we discuss our findings and, by integrating our findings from the survey and lesson observation, we consider implications for designing future interventions (thereby addressing RQ2). In this collaborative way, we are fairly confident of reliability of data analysis and coding.

Findings from the survey

Overall performance.

Analyses of the survey data for Q1–3 and Q4&5 are summarised in Tables  1 and 2 (%s for correct answers).

From Table 1 , showing the percentage correct for Q1–3, it can be seen that almost all students from G4 knew that the angle between adjacent edges of a cube is 90 degrees (Q1-(1)), that the angle between an edge and the diagonal of a face is 45 degrees (Q1-(2)), and that all the edges of a cube are congruent (Q2-(1)). In general, primary students found Q2-(2), Q3-(1), and Q3-(2) to be more difficult than the first three questions. For the secondary schools, almost all students from G7 managed to answer correctly Q1-(1), Q1-(2), Q2-(1) and Q4. For Q2-(2), there is a higher proportion of correct responses in G9, but about 30% of G7 and 8 were not able to answer this question correctly. About 40% of G7 students answered Q3-(1) incorrectly. About 20% of G4, 30% of G5 and 20% of G5–8 students selected “rectangle” as their answers, but more than 80% of all the grades selected either “rectangle” or “squares”. This indicate almost all students can recognise angles such as DAB as 90 degrees, but those who answered “rectangle” might have influenced by “how it looks”. All students found Q3-(2) and Q5 to be fairly difficult to answer.

Tables  3 and 4 summarise details for Q2-(2) and Q3-(2).

Table 3 , showing the details for Q2-(2), suggests that in primary schools (G4–6) about 30% of students considered that the side of the cube (AB) is the same length as the diagonal of a face (CD); see Q2-(2). By G8 about 18% of students still answered AB=CD in the given diagram.

Table 4 , showing the details for Q3-(2), suggests that, up to G8, more than 30% of students answered that the triangle was an isosceles but not equilateral, while more than 20% of students in G4–8 considered the triangle in the given diagram contained a right angle. Table 4 also shows that the majority of students answered the triangle would be an isosceles, or right-angled isosceles, indicating that they might have been influenced by the visual appearance of the given diagram. Q3-(2) requires more than one step of reasoning (identifying diagonals in each face→diagonals are equal→equilateral triangle), and it is expected this problem might be difficult for G6, but it was rather surprising there is no improvement until G9.

The above data suggest that, overall, there might be gaps across the grades between the set of questions (Q1-(1), Q1-(2), Q2-(1)), (Q2-(2), Q3-(1)) and question (Q3-(2)) (and [Q5] in secondary schools). In order to confirm this, we conducted 2LPM analysis in order to gain further insight into the findings, in particular examining each question item in terms of their difficulties. Figure 3 (G4–9, Q1-(1)~Q3-(2)) and Fig.  4 (G7–9, Q1-(1)~Q5) show the relationships between each question in terms of the difficulties, and discriminations, alongside the best-fitted logistic curves for each question.

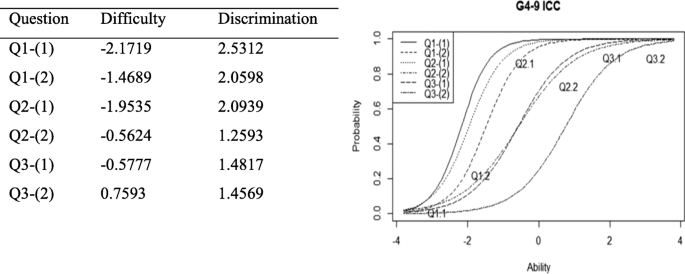
Values in each question (left) & Item characteristic curves (right) for G7–9

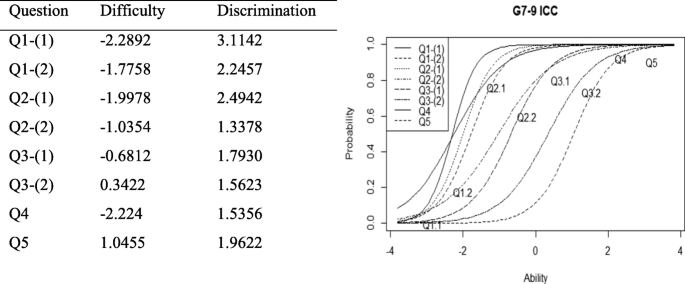
The relative difficulties listed in Figs.  3 and 4 indicate the following for G4–9 students: the relative difficulties for Q1-(1), Q1-(2) and Q2-(1) are similar; the difficulties of Q2-(2) and Q3-(1) are similar and more difficult than the first 3 questions, and Q3-(2) is confirmed as more challenging than the other questions until G9. Q5 is the hardest question for secondary school students. These two figures and 2PLM suggest that there are gaps between (Q1-(1), Q1-(2), Q2-(1)), (Q2-(2), Q3-(1)) and (Q3-(2)) (and [Q5] in secondary schools). The values of the discrimination for each questions are above 1, indicating all the items discriminate relatively well between low-skilled and high-skilled students. The overall analysis also suggests that there are difficulty gaps in Q2-(2), Q3-(2) or Q5, and we further explore what spatial reasoning and domain-specific knowledge were used to answer these questions correctly/incorrectly by focusing on Q2-(2) and Q5.

Reasoning skills and knowledge used by G4–6 students for Q2-(2)

When we examined Q2-(2) (in which G4–6 students were asked to write their reasoning), we noted that students whose explanations included the word “a diagonal (of square)” or “slanting” tend to answer this question correctly, although not many students provided such explanations. For example, 18/216 G4, 38/213 G5, and 57/209 of G6 students used a word “a diagonal of square” in their reasoning why CD > AB, and of these students who used “a diagonal”, 61.1%, 89.5% and 75.4% of G4–6 students answered Q2-(2) correctly. This indicates that these students used their domain-specific knowledge that “in a square, diagonals are longer than sides”, a type 3 answer (some of them might have also used spatial visualisation skills but we could not see explicitly from the written answers). However, if students have “incorrect” domain-specific knowledge for cubes such as “in a cube, all the sides including diagonals are equal (in Japan, ‘sides (辺)’ for both 2D and 3D shapes but not ‘edge’), then such students’ property-based spatial analytic reasoning was represented by ‘AB=CD’ as ‘AB and CD are ‘sides’ of cube, and in cube all sides are equal”. The majority of the students who answered AB=CD gave this explanation, i.e. type 2A answer. This might indicate that the use of correct domain-specific knowledge (in this case “faces of cube are squares” and “in a square, diagonals are longer than sides”) explicitly is important to solve this problem.

We also noted that some students additionally explicitly used spatial visualisation skills as evidenced by students’ answers such as “It is easier to solve this question by imagining a net of a cube” (G6) or by them adding further drawings, e.g. “when we compare a side of square and other lines, then the line becomes more distant when it goes middle”, as illustrated in Fig.  5 Although not many in our sample, such answers were categorised as type 3.

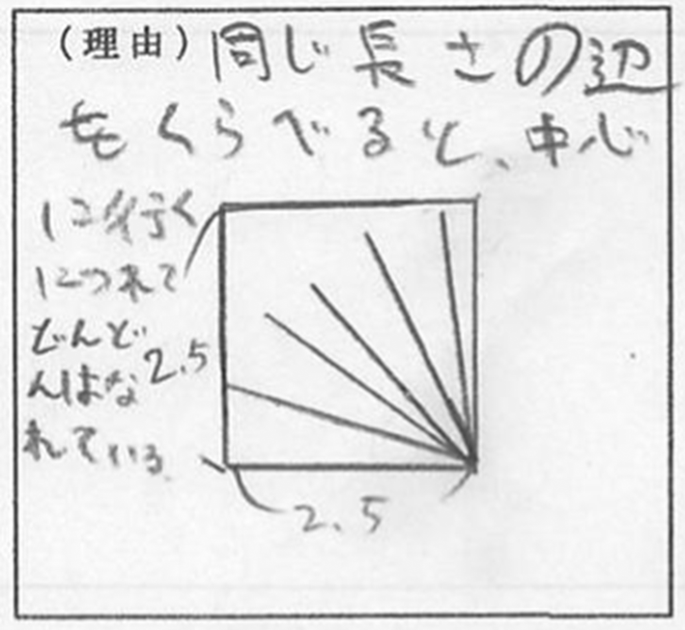
An explanation for Q2–2

Reasoning skills and knowledge used by G7–9 students for Q5

Table 5 summarises students’ answer for Q5 in terms of the types of errors:

Type 1: Incorrect answer led by 2-dimensional or intuitive global judgments, e.g. answers such as 90° with no reason stated, “looks like 90°”, “Maybe (90°)” without stating any reasons or manipulations in their answers.

Type 2A: Incorrect answer only led by property-based spatial analytic reasoning but with logical gaps or influenced by visual information, and/or incorrect/inappropriate domain-specific knowledge , e.g. answers such as “∠AEF=90°. 90/2 = 45°”, “the face ABFE and ADHE are perpendicular to each other, and BE and ED are on these faces, so 90°”, “∠BEA + ∠DEA = 45° + 45° = 90°”, etc.

Type 2B: Incorrect answer with only spatial visualisation s but influenced by visual information and/or incorrect/inappropriate domain-specific knowledge , e.g. answers such as “(drawing a net), and then 45°+45°=90°”, “(changing the orientation of the given figure) 90°”, “Looking the given from the above (mentally), it will be 90°”, etc.

Type 2C: Incorrect answer with the use of spatial visualisation and property-based spatial analytic reasoning but influenced by visual information and/or incorrect/inappropriate domain-specific knowledge . Here, triangle BDE is (mentally or on the diagram) extracted and seen as isosceles, and then inappropriate knowledge is used, e.g. “in △BDE, because ∠D=∠E=45° and it will be 90°”, “∠DAB is 90° and ∠BED is just an adjusted from ∠DAB, so it is 90°”, “in a triangle BDE, ∠B=90°, ∠D=60° and therefore 30°”.

Type 3: correct answer with valid use of spatial visualisation and/or property-based spatial analytic reasoning with correct domain-specific knowledge , e.g. answers such as “in triangle BDE, DE = EB = BD and therefore ∠BED = 60°”, “EB, ED and BD are all the diagonal of the same square. Since all the sides are equal to each other, it is an equilateral triangle (and therefore 60°)”.

From Table 5 , giving the percentages of types of answers for Q5, students in G7 and G8 did use various approaches to solve Q5, but they relied either on only property-based spatial analytic reasoning (type 2A) or only spatial visualisation (type 2B) as well as being influenced by the perceptual appearance of the given diagram. More G9 students answered Q5 correctly (37.8%) compared to G7 and 8, but 18.7% of them still relied on global judgement or provided no explanation for their answer.

When we examined the students’ explanations for their answers, it seems that students who used “in a cube, diagonals of each face are equal” were likely to give a correct answer. In G9, for example, 89 (37.8% of G9) students answered this question correctly, and within these 89, 50 of them explicitly used such knowledge to deduce the triangle is an equilateral. For G8, 32 students answered Q5 correctly, and 15 of them used “diagonals” in their explanations (in G7 but 6 of 26 who answered Q5 correctly did so). This might imply, similar to the case for Q2-(2), that domain-specific knowledge coordinates between spatial visualisation and property-based spatial analytic reasoning .

Summary of the survey results

Reflecting on the survey results and analyses described above, the following matters are suggested in terms of the use of spatial reasoning skills and domain-specific knowledge and types of answers:

Descriptive statistics and 2PLM analysis that we present suggest that gaps (in the context of our survey questions) exist between (Q1-(1), Q1-(2), Q2-(1)), (Q2-(2), Q3-(1)) and (Q3-(2)) (and [Q5] in secondary schools) across the grades.

Examining the students’ explanations for Q2-(2) and Q5 further in terms of the types of answers, one of the spatial reasoning skills (such as Type 2A or 2B), or two skills without domain-specific knowledge (Type 2C), might not be enough to answer this question correctly. In other words, to support students’ successful problem solving from type 1/2A/2B/2C to 3, it is important to encourage them not only to use spatial reasoning skills but also to make it explicit what knowledge can be used.

These findings imply (a) more research is needed to understand further the processes when students use spatial reasoning skills and domain-specific knowledge ; in particular, considering how to support students successful with types 1/2A/2B/2C to develop to be successful with type 3, and (b) learning opportunities could be provided much earlier than G8 as data from Q3-(2) point to 3 years of no improvement. This is important as in G9 students learn the Pythagorean theorem and apply this to find the lengths of diagonals in a cube, but about 30% of the students might not be able to answer Q2-(2) and 65% unable to answer 3-(2) at the end of G8 respectively, which can lead G9 students to learn superficial procedures to find the length by using the theorem without seeing the structure of cubes, for example.

Findings from lesson observation

Overall lesson progressions.

As stated in the methodology, 34 students worked with Q5 during a 45-min lesson. In the lesson, Mr. T first introduced the problem (Q5), confirming that the objective of the lesson was to find the size of angle BED. The first stage of the lesson was for the students to attempt to solve the question individually. As expected, at this stage, they used a range of different spatial reasoning skills but almost no student concluded the angle might be 60°. Many of them used only property-based spatial analytic reasoning (type 2A) or spatial visualisation skills (type 2B) (Fig.  6 ). At this stage, it is not clear what domain-specific knowledge was used for many students.

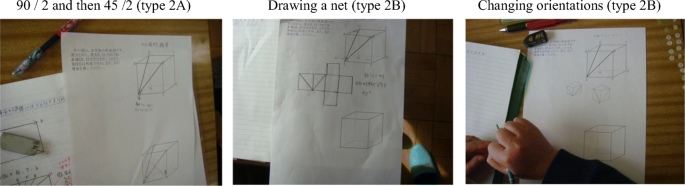
Students’ initial attempts

The next stage of the lesson was for the students to start exchanging their ideas and answers, but the diversity of answers and approaches they had used meant that they could not improve their answers or extend their initial ideas through discussions.

SW, our case students, first visualised a pyramid from the given representation, and then rotated it to another pyramid ( spatial visualisation , Fig.  7 left). After this, she seemed to visualise BDE as “an isosceles triangle” on the given diagram (Fig. 7 centre), and then tried to determine the size of the angle EDA, which she thought was 45° (indicating type 2C answer). She then had a quick conversation with student AO who sat in front of her, whose answer was 90°. SW was not convinced by this as the angle “did not look like” 90°. During their conversation, SW and AO extracted a triangle ( spatial visualisation ), and, interestingly, almost identified the triangle would be an equilateral in order to deduce the size of the angle ( property-based spatial analytic reasoning ) as follows:

SW: (pointing the two lines the diagram) They are the same (lengths)…

AO: An isosceles triangle?

SW: An equilateral triangle?

AO Then, the sum of the angles is 180°. Then because all the angles are equal in equilateral, so 60, 60, 60, and this area (incorrectly used ‘area’ to say an angle), we can see this from the front (mentally rotating the given diagram) … (then looking again the extracted triangle, and showed a confused face without any words).

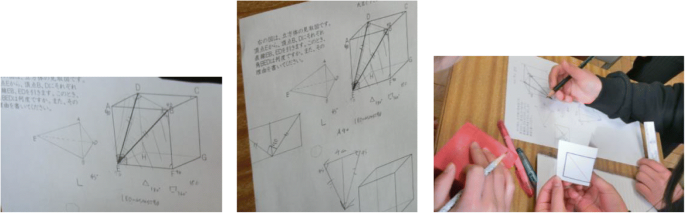
SW’s attempts

However, SW was not convinced as the triangle on the diagram still did not “look like” an equilateral, but visualised the extracted triangle as an isosceles (Fig. 7 centre). At this point, both of them also did not use explicit domain-specific knowledge specifically related to cube (e.g. diagonal), but those related to triangles which is inappropriate to reach a correct answer (indicating Type 2C answer). SW remained unsure about her answer, and exchanged various opinions with other students who sat around her, including by holding paper (Fig. 7 , right). Then AO started explaining why 90°, which is her answer, can look “narrower” in the given diagram:

AO: If you see my pencil from the above, it looks longer and from the side, it looks shorter. It is like that.

SW: Ah, I see now… I see, I need to open it (meaning to write a net, drawing additional diagrams, Fig. 6 right). So, it is 90°?

At this point, the statement “If you see my pencil from the above, it looks longer and from the side, it looks shorter. It is like that.” by AO spurred SW to draw additional diagrams ( spatial visualisation ) and she used the property of an isosceles triangle to deduce the angle would be 90° ( property-based spatial analytic reasoning ). This can be seen as type 2C as her answer was influenced by visual information and inappropriate knowledge in this problem context.

SW then went to see student OKY who explained to her that his answer was 60° because of the equilateral triangle (Fig. 7 left, OKY drew another triangle to visualise an equilateral triangle, type 3). SW seemed to be quite satisfied with OKY’s answer and explanation.

SW then tried to explain to student AO what she heard from student OKY, but SW was confused as she could not reproduce (Fig.  8 right) what she saw in OKY’s answer. Our observational notes recorded her statements which were related to spatial visualisation such as “we can draw from the front (meaning the other direction)”, “How did he do? How?”, “Something was turned to an equilateral”, etc. (Fig. 8 right) She also did not use statements such as “In cube, diagonals of each face are …” at all, but used indicative words such as “there” or “here” to point the elements of the shapes out. At this point, she wrote 45° and 60° on her sheet. The thinking processes observed from SW indicate that SW managed to use both/either spatial visualisation and/or property-based spatial analytic reasoning but because of the lack of domain-specific knowledge , her reasoning remained up to 2C, and could not advance to type 3 by herself.

OKT (left) and SW (right)’s answers

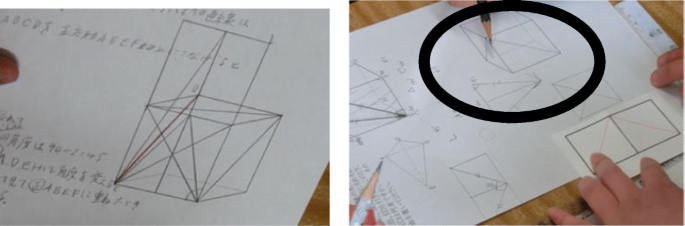
Soon after, Mr. T asked the student to stop working individually/with groups, and invited a few students to explain their reasoning. Student CA showed his answer as follows:

CA: First, here, first it is written from here (D and B) to there, the angle is written there, but when we rotated it …

Students: (whispering) (my answer is) 22.5…

CA: … then it (the angle BED) will be the same angle of this one (in the rotated triangle in red in the figure below). When we consider with the rotated shape, then when we connect diagonals, diagonals, and diagonals of a square, and this is an equilateral triangle. The sum of the angle is 180°, and since their angles and sides are equal, we divide 180° by 3, and then it will be 60°.

In his explanation in Fig. 9 , CA rotated the given diagram ( spatial visualisation , also on the board it is written “回して見ると (rotating and then see)”, indicating thinking by rotating, next to the diagram) and then used the diagonals of a square and the properties of triangles (sum of the angles and equilateral triangle) to deduce the angle is 60° ( property-based spatial analytic reasoning ), type 3 answer. Here, domain-specific knowledge “in cube, diagonals of each face are equal” explicated and represented by “the diagonals of a square” coordinate his spatial visualisation and property-based spatial analytic reasoning and enabled him to identify the triangle is equilateral . This explanation (type 3) by CA seemed to be accepted by other students in the class, including SW who nodded during CA’s explanation of his reasoning. After the explanation, SW managed to reproduce OKY’s answer of 60° (Fig.  10 ).

CA’s explanation why the angle BED is 60°

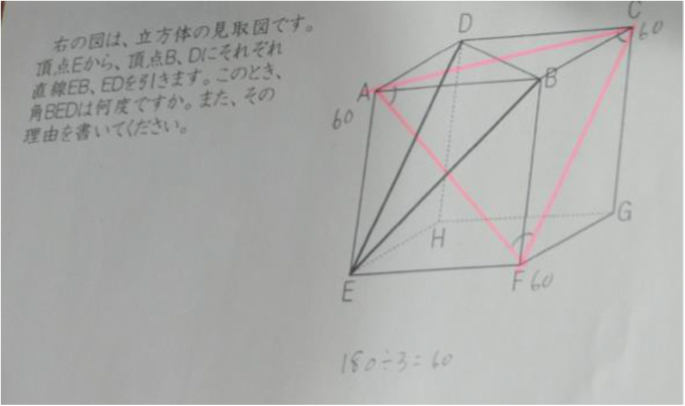
SW’s final answer

Mr. T praised the student’s efforts and CA’s answer, asked them to finished their work, and complete the post-lesson problem (which, rather than finding angle BED, was to find the size of angle FCH). With that, the lesson finished.

Pre-/post-survey results

Prior to the research lesson in February 2019, students took the pre-survey (Fig. 1 ) in December 2018. One month after the lesson, the students took the post-survey (using the same survey). They were also asked to solve Q5 with the different angle (FAH). We do not claim that only one lesson make a positive impact on students’ s patial reasoning skills , but we are interested in how the learning experience of the lesson made any changes in the students’ answers. Table 6 summarises the results from the both surveys.

From Table 6 , while the pre-survey results by this class was a bit lower than our main survey result, in the delayed post-survey their performance was generally an improvement on the pre-survey and the main survey. There was a significant difference in the pre-test ( M  = 3.89, SD = 1.64) compared to the post-test ( M  = 4.7, SD = 1.5), t(33) = 3.1, p  < .005).

What is more, 41.2% of the students answered Q3-(2) correctly, which is higher than G8 performance (35.3%) in the main survey. For the Q5 (finding FAH), 70.6% of the students answered correctly. Considering that the post-survey was undertaken 1 month after the lesson, the results suggest that about 17 students (of 34) demonstrated good spatial reasoning skills as well as retaining what they learnt well after the lesson. Nevertheless, there were 6 students who did not show much difference from before to after the lesson.

Reflecting on the lesson observation, the pre/post-survey and its analyses described above, the following matters are suggested:

G6 students used various spatial reasoning skills to tackle Q5. Similar to secondary school students, five types of answers were observed. It seems many students initially showed type 2A and 2B answers without extracting the triangle BDE.

Discussions between the students were useful to exchange various ideas and answers, and this encouraged the students to think deeply about what they have done in terms of spatial visualisation and property-based spatial analytic reasoning , making them decide what triangle BDE would be. However, their answer remained as type 2C. In order to harmonise the two spatial reasoning skills, the explicit use of domain-specific knowledge appropriate in the problem context might be more encouraged, exemplified by the case of student SW.

In the next section, we explore and integrate what our findings from the main survey and lesson observation imply in terms of our research question and the theoretical framework.

The importance of the spatial reasoning (e.g. Lowrie 2012 ; Lowrie et al. 2018 ; Mulligan et al. 2018 ; Lowrie et al. 2019 ) and relationships between different spatial skills and reasoning (Pittalis and Christou 2010 , 2013 ) are documented in existing studies. The aim of this paper was to explore how the students across the grades use spatial reasoning skills and domain-specific knowledge to solve geometrical problems (RQ1), and what can be learnt to inform future interventions to improve students’ spatial skills and reasoning (RQ2). By following Battista et al. ( 2018 ), we took spatial reasoning skills as spatial visualisation and property-based spatial analytic reasoning , and domain-specific knowledge which coordinates these two skills. We then categorised the types of answers and analysed the survey data from 1357 students across G4–9, and lesson observation from a G6 class.

Similar to existing studies, our survey results and lesson observation revealed that both spatial visualisation and property-based spatial analytic reasoning play important roles, but that, without appropriate domain-specific knowledge , students’ reasoning can be influenced by the visual appearance of the geometrical objects in the problems (e.g. Ufer et al. 2008 ; Chinnappan et al. 2012 ). In particular, when problems have more than one step of reasoning (e.g. Q3-(2) or Q5 in our case), such problems remain challenging across the grades.

The contribution of our analysis of our data is that we found that the categorisation of five types of answers accounted for the ways students could not answer the survey problems correctly. For example, when students solved, for example, Q5, they might manage to use spatial visualisations such as rotating mentally the given diagrams, extract triangles, change their points of view etc. (type 2B for example), but they struggled to determine what the triangle would be. Similarly, they could use reasoning based on properties of shapes ( property-based spatial analytic reasoning ) but they still reached incorrect answers (e.g. type 2A or type 2C), because they were incorrect/inappropriate. This might be caused by the given diagrams’ visual appearance, i.e. the dual process (Van Hoof et al. 2013 ) or uncontrollable images (Aspinwall et al. 1997 ).

What is more, our findings suggest that the students who explicitly used domain-specific knowledge which was appropriate for the problem (e.g. “in cube, diagonals of each face are equal”) were likely to reason correctly for the given problems (e.g. students’ explanations for Q2-(2) or Q5 in the main survey or the case of CA). In particular, the effective use of domain-specific knowledge might enable students to break an impasse of reasoning (2A-2C) for successful reasoning (2C).

Given our findings discussed above, our answer to our RQ1 is that the students across the grades can use spatial reasoning skills , but for problems with more than one step of reasoning, students need to make their domain-specific knowledge explicit in problem solving, in particular which knowledge should be chosen and why. Fischbein ( 1993 ) calls this productive reasoning (also what Llinares and Clemente 2019 , call configural reasoning ), and we argue that it is domain-specific knowledge that coordinates visual and conceptual aspects in 3D geometry problem solving.

Our study reveals that although there are some improvement across the grades, certain problems such as Q3-(2) do not improve much from G6–8. Also many G9 students struggle to answer correctly Q5. This is an issue for, say, upper secondary schools in trigonometry, when students might be asked to solve various questions in trigonometry, e.g. finding areas of triangles formed in a cube, etc. However, existing studies also suggest that spatial reasoning skills can be improved by certain interventions (e.g. Lowrie et al. 2019 ). A positive result in the post-survey result (Table 6 ) suggests that it is possible to implement a lesson with a problem even G9 students find difficult, and even though it was only one lesson, about half of the G6 students retained what they experienced in this lesson well even after 1 month. This implies that current Japanese curriculum for 3D geometry should be re-examined, and more learning opportunities might be given to both primary and secondary school students in which they can not only exercise their spatial reasoning skills but also consolidate and share, discuss and explicitly use what they have as domain-specific knowledge for productive (or configural ) reasoning (in this paper this was exemplified as encouraging reasoning based on type 2A, 2B or 2C to type 3), which is an answer to our RQ2.

Conclusion and limitation of the study

We consider that our findings are significant as this is one of the first studies to use the same survey questions to see how students in each grade perform certain geometry problem solving, and what kind of difficulties they show. In this paper, we mainly relied on students’ written evidence and thinking processes observed in one lesson, but our approach has certain limitations. Amongst the limitations, our data and approach is not enough to scrutinise why and how students chose particular spatial reasoning skills and domain-specific knowledge . Such metacognitive aspects are missing in this paper and are worthy of consideration in future research.

While we have deepened insight into the use of spatial reasoning skills in geometry across the grades, our findings are based on the survey questions used in this study. Taking a factor analysis approach, as Pittalis and Christou ( 2010 ) did in constructing a model for specific and general spatial reasoning skills with a wider range of different question items, is something to consider for future research. Gaining further insights into how the spatial reasoning skills revealed in our study might be related to other areas of mathematics such as proving or algebraic reasoning is also something we would like to undertake in our future research.

Aspinwall, L., Shaw, K. L., & Presmeg, N. C. (1997). Uncontrollable mental imagery: graphical connections between a function and its derivative. Educational Studies in Mathematics, 33 (3), 301–317.

Article   Google Scholar  

Battista, M. T., Frazee, L. M., & Winer, M. L. (2018). Analyzing the relation between spatial and geometric reasoning for elementary and middle school students. In K. S. Mix & M. T. Battista (Eds.), Visualizing Mathematics: the role of spatial reasoning in mathematical thought (pp. 195–228). Cham: Springer.

Chapter   Google Scholar  

Chinnappan, M., Ekanayake, M. B., & Brown, C. (2012). Knowledge use in the construction of geometry proof by Sri Lankan students. International Journal of Science and Mathematics Education, 10 (4), 865–887.

Duval, R. (2017). In M. Tania & M. Campos (Eds.), Understanding the mathematical way of thinking: the registers of semiotic representations . Cham: Springer.

Fischbein, E. (1993). The theory of figural concepts. Educational Studies in Mathematics, 24 (2), 139–162.

Fujita, T. (2012). Learners’ level of understanding of the inclusion relations of quadrilaterals and prototype phenomenon. The Journal of Mathematical Behavior, 31 (1), 60–72.

Fujita, T., Kondo, Y., Kumakura, H., & Kunimune, S. (2017). Students’ geometric thinking with cube representations: assessment framework and empirical evidence. The Journal of Mathematical Behavior, 46 , 96–111.

Gillard, E., Van Dooren, W., Schaeken, W., & Verschaffel, L. (2009). Dual processes in psychology of mathematics education and cognitive psychology. Human Development, 52 , 95–108.

Jones, K., & Tzekaki, M. (2016). Research on the teaching and learning of geometry. In A. Gutiérrez, G. C. Leder, & P. Boero (Eds.), The second handbook of research on the psychology of mathematics education (pp. 109–149). Rotterdam: Sense Publishers.

Kondo, Y., Fujita, T., Kunimune, S., Jones, K., & Kumakura, H. (2014). The influence of 3D representations on students’ level of 3D geometrical thinking. In Proceedings of PME 38 and PME-NA 36 (Vol. 4, pp. 25–32).

Google Scholar  

Llinares, S., & Clemente, F. (2019). Characteristics of the shifts from configural reasoning to deductive reasoning in geometry. Mathematics Education Research Journal, 31 (3), 259–277.

Lowrie, T. (2012). Visual and spatial reasoning: the changing form of mathematics representation and communication. In B. Kaur & T. L. Toh (Eds.), Reasoning, communication and connections in mathematics: Yearbook 2012, Association of Mathematics Educators (pp. 149–168). Singapore: World Scientific.

Lowrie, T., Logan, T., Harris, D., & Hegarty, M. (2018). The impact of an intervention program on students’ spatial reasoning: Student engagement through mathematics-enhanced learning activities. Cognitive Research: Principles and Implications, 3 (50), 1–10.

Lowrie, T., Logan, T., & Hegarty, M. (2019). The influence of spatial visualization training on students’ spatial reasoning and mathematics performance. Journal of Cognition and Development, 20 (5), 729–751.

Mulligan, J., Woolcott, G., Mitchelmore, M., & Davis, B. (2018). Connecting mathematics learning through spatial reasoning. Mathematics Education Research Journal, 30 (1), 77–87.

Parzysz, B. (1991). Representation of space and students’ conceptions at high school level. Educational Studies in Mathematics, 22 (6), 575–593.

Pittalis, M., & Christou, C. (2010). Types of reasoning in 3D geometry thinking and their relation with spatial ability. Educational Studies in Mathematics, 75 (2), 191–212.

Pittalis, M., & Christou, C. (2013). Coding and decoding representations of 3D shapes. The Journal of Mathematical Behavior, 32 (3), 673–689.

Sijtsma, K., & Molenaar, I. W. (2002). Introduction to nonparametric item response theory (Vol. 5). Thousand Oaks: Sage.

Book   Google Scholar  

Sinclair, N., & Bruce, C. D. (2015). New opportunities in geometry education at the primary school. ZDM Mathematics Education, 47 (3), 319–329.

Sinclair, N., Bussi, M. G. B., de Villiers, M., Jones, K., Kortenkamp, U., Leung, A., & Owens, K. (2016). Recent research on geometry education: An ICME-13 survey team report. ZDM, 48(5), 691–719.

Ufer, S., Heinze, A., & Reiss, K. (2008). Individual predictors of geometrical proof competence. Proceedings of the Joint Meeting of PME 32and PME-NA XXX (Vol. 4, pp. 361–368).

Van Hoof, J., Lijnen, T., Verschaffel, L., & Van Dooren, W. (2013). Are secondary school students still hampered by the natural number bias? A reaction time study on fraction comparison tasks. Research in Mathematics Education, 15 (2), 154–164.

Download references

Author information

Authors and affiliations.

University of Exeter, 79 Heavitree Rd, Exeter, EX1 2LU, UK

Taro Fujita

Nara University of Education, Nara, Japan

Yutaka Kondo

Shizuoka University, Shizuoka, Japan

Hiroyuki Kumakura & Susumu Kunimune

University of Southampton, Southampton, England

Keith Jones

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Taro Fujita .

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Fujita, T., Kondo, Y., Kumakura, H. et al. Spatial reasoning skills about 2D representations of 3D geometrical shapes in grades 4 to 9. Math Ed Res J 32 , 235–255 (2020). https://doi.org/10.1007/s13394-020-00335-w

Download citation

Received : 30 October 2019

Revised : 13 April 2020

Accepted : 02 May 2020

Published : 27 May 2020

Issue Date : June 2020

DOI : https://doi.org/10.1007/s13394-020-00335-w

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Spatial reasoning
• Domain-specific knowledge of geometrical shapes
• 2D representations
• Find a journal
• Publish with us
• Track your research

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 7: Area and perimeter

About this unit, count unit squares to find area.

• Intro to area and unit squares (Opens a modal)
• Measuring rectangles with different unit squares (Opens a modal)
• Measuring area with partial unit squares (Opens a modal)
• Creating rectangles with a given area 1 (Opens a modal)
• Creating rectangles with a given area 2 (Opens a modal)
• Find area by counting unit squares 7 questions Practice
• Find area with partial unit squares 7 questions Practice
• Create rectangles with a given area 4 questions Practice

Area of rectangles

• Transitioning from unit squares to area formula (Opens a modal)
• Finding missing side when given area (Opens a modal)
• Counting unit squares to find area formula (Opens a modal)
• Area of rectangles review (Opens a modal)
• Transition from unit squares to area formula 7 questions Practice
• Find a missing side length when given area 7 questions Practice
• Perimeter: introduction (Opens a modal)
• Perimeter of a shape (Opens a modal)
• Find perimeter by counting unit squares (Opens a modal)
• Finding perimeter when a side length is missing (Opens a modal)
• Finding missing side length when given perimeter (Opens a modal)
• Perimeter & area (Opens a modal)
• Perimeter and unit conversion (Opens a modal)
• Applying the metric system to perimeter (Opens a modal)
• Perimeter review (Opens a modal)
• Find perimeter by counting units 4 questions Practice
• Find perimeter when given side lengths 7 questions Practice
• Find a missing side length when given perimeter 4 questions Practice

Area of parallelograms

• Area of a parallelogram (Opens a modal)
• Area of parallelograms (Opens a modal)
• Area of parallelograms 4 questions Practice
• Find missing length when given area of a parallelogram 4 questions Practice

Area of triangles

• Area of a triangle (Opens a modal)
• Area of triangles (Opens a modal)
• Area of triangle proof (Opens a modal)
• Find base and height on a triangle 4 questions Practice
• Area of right triangles 4 questions Practice
• Area of triangles 7 questions Practice
• Find missing length when given area of a triangle 4 questions Practice

Area of shapes on grids

• Area of a triangle on a grid (Opens a modal)
• Area of a quadrilateral on a grid (Opens a modal)
• Areas of shapes on grids 4 questions Practice

Area of trapezoids & composite figures

• Area of trapezoids (Opens a modal)
• Area of kites (Opens a modal)
• Finding area by rearranging parts (Opens a modal)
• Area of composite shapes (Opens a modal)
• Perimeter & area of composite shapes (Opens a modal)
• Challenge problems: perimeter & area (Opens a modal)
• Area of trapezoids 4 questions Practice
• Area of composite shapes 4 questions Practice
• Area challenge 4 questions Practice

Area and circumference of circles

• Radius, diameter, circumference & π (Opens a modal)
• Labeling parts of a circle (Opens a modal)
• Radius, diameter, & circumference (Opens a modal)
• Circumference review (Opens a modal)
• Radius & diameter from circumference (Opens a modal)
• Area of a circle (Opens a modal)
• Area of circles review (Opens a modal)
• Area of a circle intuition (Opens a modal)
• Radius and diameter 7 questions Practice
• Circumference of a circle 4 questions Practice
• Area of a circle 7 questions Practice
• Area of parts of circles 4 questions Practice

Advanced area with triangles

• Area of equilateral triangle (Opens a modal)
• Area of equilateral triangle (advanced) (Opens a modal)
• Area of diagonal-generated triangles (Opens a modal)

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• Knowledge Base
• Math for kids

2D And 3D Shapes Worksheets

Created: May 12, 2022

Last updated: June 5, 2023

Has your kid started learning geometry in class yet? If yes and you want to mix things up a little bit, read on!

2D and 3D shapes worksheets are here to enhance your child’s math experience. Most students love the topic of shapes and will enjoy learning more about them through creative worksheets.

Identifying 2D And 3D Shapes Worksheet

Sort 2D And 3D Shapes Worksheet

2D And 3D Shapes Worksheet

Sorting 2D And 3D Shapes Worksheet

Comparing 2D And 3D Shapes Worksheet

3D And 2D Shapes Worksheets

Importance of 2D and 3D Shapes Worksheets

2D shapes have properties like sides, angles, lengths, and widths, while 3D shapes feature volume, length, width, and height.

The first skill children develop by studying with 2D and 3D shape worksheets is logic. For example, when making a Venn diagram with circles, kids think through all possible outcomes before choosing one or more ways of solving the problem.

Math for Kids

Another important skill that children develop is the ability to imagine things in their minds. By imagining 2D and 3D shapes and then drawing them on paper, kids develop the ability to visualize objects like letters and numbers in space.

You can use worksheets to help your students learn more about these two types of shapes. For example, during an art lesson, you can use worksheets to show students how shapes can be used to create various objects, such as a flower or a butterfly.

2D And 3D Shapes Worksheets PDF

2D And 3D Shape Worksheets

Free Printable 2D And 3D Shapes Worksheets

2D 3D Shape Worksheets

Identify 2D And 3D Shapes Worksheets

Also, 2D, 3D shapes worksheets are a great way to introduce kids to math concepts such as area, perimeter, and volume all of which will be useful when they get older.

In addition to helping children learn about 2D and 3D shapes, worksheets will help understand math concepts such as addition, subtraction, and multiplication and the way they relate to each other in space and time.

Lastly, another way to use 2D and 3D shapes worksheets is offering them as a homework assignment. If a child has forgotten what an octagon looks like or how to draw a rectangle, they can use a worksheet to refresh knowledge on the features of each shape.

More Shapes Worksheets

• Shapes Worksheets For Kindergarten
• 3D Shapes Worksheets
• 3D Shape Worksheets Kindergarten
• Shape Tracing Worksheets
• Shapes Worksheets Preschool
• Shapes Worksheets

As a seasoned educator with a Bachelor’s in Secondary Education and over three years of experience, I specialize in making mathematics accessible to students of all backgrounds through Brighterly. My expertise extends beyond teaching; I blog about innovative educational strategies and have a keen interest in child psychology and curriculum development. My approach is shaped by a belief in practical, real-life application of math, making learning both impactful and enjoyable.

Struggling with Geometry?

• Does your child need extra assistance with mastering geometry lessons?
• Start learning with an online tutor.

Kid’s grade

Is your child finding it hard to understand the concept of geometry? An online tutor could be of help.

After-School Math Program

Related worksheets.

Study the number 14 in a fun way using number 14 worksheets that are ideal for kindergarteners or grade 1 students who learn to count and recognize a set of numbers. Number 14 Addition Worksheets You can use number 14 worksheets for preschoolers to boost your child’s addition skills. These number worksheets help kids practice […]

Also called the greatest common divisor, the greatest common factor is an important math concept that comes in handy when solving fraction problems. These greatest common factor worksheets will help students find the greatest common factor of given numbers. Before downloading the greatest common factor worksheets PDF, let’s learn about GCR and its benefits. What […]

Inequalities are no fun for an average young learner. They’re even less fun when you throw a word problem into the mix. More often than not, learners may encounter a math question that looks somewhat like this: Jake and Hannah were asked to take 850 baskets of apples to the farmer’s market. Jake took 200 […]

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

The home of mathematics education in New Zealand.

• Forgot password ?
• Resource Finder

2D to 3D: Working with shapes and representations

The Ministry is migrating nzmaths content to Tāhurangi.             Relevant and up-to-date teaching resources are being moved to Tāhūrangi (tahurangi.education.govt.nz).  When all identified resources have been successfully moved, this website will close. We expect this to be in June 2024.  e-ako maths, e-ako Pāngarau, and e-ako PLD 360 will continue to be available. 

For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths

In this unit students interpret 2-dimensional representations of 3-dimensional objects and learn to create their own representations.

• Construct plan views of solid objects.
• Create nets that fold to form solid objects.
• Classify 3-dimensional shapes by their properties.
• Identify 3-dimensional shapes in the environment.

Plan views are different drawings of the same building. These drawings are commonly seen in house design and usually show the structure from above (top or seagull view), front, and side.

In this unit, students study solid (3-dimensional) shapes. Some solids are polyhedral. A polyhedron (singular) is a three-dimensional solid object that consists of a collection of polygons (flat shapes) that bound (enclose) a space. Students learn about prisms and pyramids which are classes of polyhedra (plural). In the figure below, the cube, cuboid, hexagonal prism, and triangular prism all have a constant cross-section if cut parallel to the end faces. Having a constant cross-section is the defining property of a prism. A cylinder is similar to a prism, however, because it has a curved surface, it is not technically a polyhedron.

Pyramids have a base that names the pyramid (e.g. square), and triangular faces that converge at a point, the apex. The figure below shows square-based and triangular based (tetrahedron) pyramids. A cone is similar to a pyramid in the same way that a cylinder is similar to a prism, as it has a curved surface, which means it is technically not a polyhedron.

In this unit students explore creating nets which are flat patterns that fold to form a solid. Nets are important in the packaging and construction industries. 

The learning opportunities in this unit can be differentiated by providing or removing support to students, by varying the task requirements. Ways to support students include:

• providing materials, such as physical or digital models of 3-dimensional solids, so students can move and manipulate these, and themselves, in relation to the objects
• explicitly modelling the building and drawing of shapes from various viewpoints, so students appreciate the minimal requirements of plan views. This could include the use of digital cameras
• altering the complexity of the shapes students are asked to construct
• providing access to sculpting materials, such as plasticine, so students can create their own 3-dimensional models
• orientating cube models so the viewpoint matches the orientation of isometric paper
• providing opportunities for students to work in groups and pairs to encourage collaboration, peer-sharing of ideas, questioning, and reciprocal learning

Tasks can be varied in many ways including:

• manipulating the complexity of the 3-dimensional objects the students represent
• scaffolding the process of representational drawing into a sequence of steps.

The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students, and to make connections with current events and relevant learning from other curriculum areas. Build on the interests of your students. Many buildings throughout the pacific are examples of prisms so are ideal for this unit. For example, traditional whare and fale were usually the shape of pentagonal prisms. Students might also be motivated by interesting local buildings or iconic structures from around the world (perhaps from cultures that are relevant to their heritage). You could choose one context to frame all problems in, or vary the contexts presented in each problem.

Te reo Māori kupu such as raumata (net of a solid figure) and the names for different shapes could be introduced in this unit and used throughout other mathematical learning

• Interlocking cubes
• Cuisenaire Rods (optional - a digital representation could also be used. Search online for interactive Cuisenaire Rods )
• Geometric solids (Prisms, pyramids, spheres, etc.) (Useful)
• Polydrons, Geoshapes, or other interlocking plastic polygons (a digital representation could also be used. Search online for interactive Shape Tool)
• Scissors, rulers, protractors, sticky tape
• PowerPoints One , Two , Three , Four  and Five
• Copymasters One , Two , Three , Four , Five , and Six

Session One

In this session students create plan views (top, front, side) of models made with connecting cubes.

• Use PowerPoint One to introduce cityscapes. Slides 1-3 show some iconic skylines from around the world. Ask students if they know the cities shown (New York, Melbourne, Shanghai). You could adapt the PowerPoint to include skylines from locations that are more relevant to your students (e.g. that reflect their heritage) Do you know where this is? How? Students might spot iconic buildings or landmarks such as rivers or harbours.
• Introduce the connecting cubes. Slides 4 – 6 show how plan views of a building can be created by lying it on a surface and viewing it from different positions. Note that the drawings are what the camera sees and do not include cubes hidden behind others. Slide 7 shows all three views simultaneously.
• Give all students some cubes and invite them to construct the building. They will need a maximum of 10 cubes each. This could be done in pairs if necessary. After a suitable time, ask students to compare their buildings and check that what they have built is correct. Model constructing the building and viewing it from different perspectives. Use the language that is used on the slide - e.g “this is the top view”. Encourage students to share any other terms they use when talking about perspective (e.g. bird’s eye view).
• Give students the puzzle on Slide 8. Ask them to work independently to create a building that matches the three views. Watch as students work. Look for the following: Do they approach the task systematically or resort to trial and error? Do they get one view correct first, the top for example, before trying to get the other views correct?

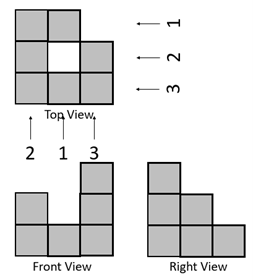
• Ask students to create their own puzzles. Provide Copymaster One to support their recording. When they are done, students can exchange their puzzle drawings with a partner to see if that student can create a matching building.

Session Two

In this session students practise making cube buildings from plan views. The session progresses to creating plan views of other objects, including common geometric solids.

• Provide students with about 15 cubes each. Show the class Slides 1-5 of PowerPoint Two , one at a time. Give students plenty of time to create their buildings and share the results with each other. The buildings get more complex as the slides progress. Look for students to apply systematic strategies, as discussed above. You might decide to create a puzzle wall with plan drawings made by students in Session One.
• Slide 6 shows plan views of a coffee cup. What do you think this object is?  Do you have enough information? Draw what the object might look like from the right side. Draw what the object might look like from the left side.
• After the students have attempted the left and right-side views animate the slide to show how lines might be used for more accuracy. An interesting point is that the width of the right and left views is the same width as the front.  Why?
• Slide 7 shows the top and left views of a cone.  What might this solid be? How do you know? Students should recognise that the front and right views are also triangles. You might take digital photographs of a cone to show the views. Many students want to show the curvature of surfaces in their plan views and require support not to do so.
• Slide 8 shows two views (top and right) of a simple house structure. What shape might this be? Sketch what you think the front view looks like.
• Animate the slide to show how construction lines support drawing the front view. Now draw the left view.
• Slide 9 shows a wharenui at Whakarewarewa village (Rotorua). This is an example of a house with a gable roof. You could edit this slide to include other wharenui, perhaps from your local area, that include gable roof.

Session Three

In this session students explore nets (flat patterns) for simple solids with the aim of connecting these to plan views. A complete unit on 3 dimensional solids is available at Level 3 at this link: Polyhedra: 3D Shapes . You may like to work through the Polyhedra Unit so students are comfortable with designing simple nets. This session builds on that work.

• Show Slide One of PowerPoint Three .  Imagine I wanted to make an architect model of this building. I would need a net or flat pattern to fold up. What shapes would be in the net? Students should recognise that the end faces of the building are pentagons (five sides).  What is a solid like this called in mathematics? (pentagonal prism) How many rectangles are needed to wrap around the pentagonal faces? (five)
• Slides 2-5 can be used to remind students how to form the net for other prisms. Slides 3-5 are animated so only the picture of the solid is visible at first. What is the mathematical name for this solid? Sketch what you think the net will look like. Note that one layout for each net is given but there are many different configurations of the set of shapes that will also work.
• Return to Slide 1 and pose the challenge. Create a net to build an architect model of this building. Take care to measure correctly so the edges match exactly. You will need to think about which edges are the same length. You might define the length of one edge to keep the models of manageable size. Eight centimetres is a good size for the width of the building.
• Provide students with 1cm grid paper ( Copymaster Two ) to make construction and measurement easier, and scissors and tape. Allow your students plenty of time to construct their nets, fold, and glue/tape them. Roam and support students with the construction, and encourage them to support each other.

An alternative is to use digital technology. Tools like PowerPoint or Google Drawings could be used. There are also a variety of freely-available tools online that allow students to manipulate shapes - search online for interactive shape tool. Using computer generated shapes, rotating, and translating them, saves time and allows for experimentation with less consequence than physical construction.

• Slide 6 shows one possible net. Animate the slide progressively using mouse clips. What other edges of the net will be the same length as this edge? What other points will join this point when the net is folded?
• Show Slide 7 but do not animate it.  Here are two views of a Manor house. Complete the drawings of the front and right views. What do you need to be careful about?
• Provide the students with Copymaster Three to draw on. Animate the slide to support students if needed. Now create a net for the architect model of this house.
• Give your students Copymaster Two to ease the measurement load and to keep lines parallel or perpendicular. Parallels and perpendiculars are an interesting point of discussion. Students may decide to build the house and annex separately. Roam while students work, looking for the following: Do they recognise that both the body of the Manor House and the annex are rectangular prisms? Do they recognise that the top of the Manor House is a square based pyramid minus the base? Do they attend to side lengths that must be equal?
• Slide 8 provides two possible nets for the Manor House and Annex though many variations also work.
• If your students require more challenge use Slides 9-11 which represent a house with a hip roof. The net is difficult to create. Copymaster Four can be used for students to draw plan views.
• After students have attempted their nets, discuss the challenges of creating the nets. What strategies were helpful? (Seeing the whole building as made of units such as a rectangular prism or a pyramid) What did you find most challenging? Which of the possible nets are best for creating architect models? (Minimising the joins creates a more robust model)

Session Four

In this session students are asked to create their own architect buildings. The intention is to create a village that can be used in Session Five.

• Look through PowerPoint Four with your students. You might choose houses that are most culturally relevant to your students. What shapes are houses and other buildings most likely to be? Why do you think those shapes are used? Why are shapes like cones and cylinders not used very much?
• We are going to create architect models for the next session. You must be able to make the building using a single sheet of grid paper ( Copymaster Two ). You can combine two shapes to make your building. I want you to be adventurous. Let’s get lots of interesting buildings.
• Provide the students with scissors, grid paper, rulers, protractors, tape, and bottles of PVA (some students might want to create tabs). Encourage students to use digital technology if it is available. Roam the room as students work. Refer them to nets of common solids if they need support. Highlight situations where edge lengths need to be equal.
• After students have sufficient time to make a model gather the class. Ensure students write their name on the base of the model. Is there a way we could group our buildings into different shapes?
• Look at how the buildings might be classified, such as, single-level and high rise, basic shape (prism, pyramid, etc.), face and curved surfaces, house and apartments, etc.
• Collect the models and locate them in a safe place.

Session Five

There are two options for this session:

• Create villages in a grid layout and challenge students to draw plan views of each village using compass directions.
• Drawing the buildings.

You might choose to do both of these activities.

Creating villages

• Use Copymaster Five to create a grid reference system. You might enlarge it to A3 to get more space.
• Place five different building models on each grid. Fix them in place with Blu-Tack or a loop of cellotape.
• Use the compass application on a mobile phone to orientate the grid, North facing North, and South facing South.
• Ask students to create place drawings of the village. You might allow them to position themselves at eye level to draw views from the West, East, and North.
• Can they draw the plan view by imaging, without needing to view the village from above?

Drawings of the buildings

• Give each student an architect model that is not their own. Ask them to draw pictures of the building that will allow another person to identify it.
• Students might use plan views, nets, perspective drawing, or their own style of representation (Cubist paintings by Picasso might inspire students).
• PowerPoint Five can be used to develop isometric drawing. The slides are animated so you can pause the slides and let students imitate the drawing to that point. Copymaster Six has isometric grid paper for students to use.
• Once drawings have been made, allocate students a drawing that is not their own. Challenge them to locate the building the drawing represents. There may be multiple candidates.

Dear family and whānau,

This week we have been exploring 3 dimensional shapes. Ask your child to explain how these solid shapes have faces, edges and vertices. We have been learning to represent solid objects with drawings on paper and make patterns that fold up to make models of the object.

You might like to look at some cardboard packets from home, open them up, and see what the net (flat pattern) looks like.

Log in or register to create plans from your planning space that include this resource.

• Printer-friendly version

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Properties of Shapes KS1

This collection is one of our Primary Curriculum collections - tasks that are grouped by topic.

Let's Investigate Triangles

Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?

Three Squares

What is the greatest number of squares you can make by overlapping three squares?

Colouring Triangles

Explore ways of colouring this set of triangles. Can you make symmetrical patterns?

Chain of Changes

Arrange the shapes in a line so that you change either colour or shape in the next piece along. Can you find several ways to start with a blue triangle and end with a red circle?

Cubes Cut Into Four Pieces

Eight children each had a cube made from modelling clay. They cut them into four pieces which were all exactly the same shape and size. Whose pieces are the same? Can you decide who made each set?

Building with Solid Shapes

We have a box of cubes, triangular prisms, cones, cuboids, cylinders and tetrahedrons. Which of the buildings would fall down if we tried to make them?

Skeleton Shapes

How many balls of modelling clay and how many straws does it take to make these skeleton shapes?

Shadow Play

Here are shadows of some 3D shapes. What shapes could have made them?

Complete the Square

Complete the squares - but be warned some are trickier than they look!

Matching Triangles

Can you sort these triangles into three different families and explain how you did it?

Inside Triangles

How many different triangles can you draw on the dotty grid which each have one dot in the middle?

What does the overlap of these two shapes look like? Try picturing it in your head and then use some cut-out shapes to test your prediction.

Can you each work out what shape you have part of on your card? What will the rest of it look like?

Exploded Squares

This practical activity challenges you to create symmetrical designs by cutting a square into strips.

Shapely Lines

This challenge invites you to create your own picture using just straight lines. Can you identify shapes with the same number of sides and decorate them in the same way?

Poly Plug Rectangles

The computer has made a rectangle and will tell you the number of spots it uses in total. Can you find out where the rectangle is?

Data Shapes

Sara and Will were sorting some pictures of shapes on cards. "I'll collect the circles," said Sara. "I'll take the red ones," answered Will. Can you see any cards they would both want?

What's Happening?

Shapes are added to other shapes. Can you see what is happening? What is the rule?

Exploring 2D Shapes

In this task, children will make shapes out of loops of string and discuss what they notice about their shapes.

Making Footprints

In this activity, children will develop an awareness of the faces of 3D shapes by using them to make 'footprints' in soft dough.

Making a Picture

This task provides an opportunity for children to work together to make a picture, discussing with each other which position they want to put each shape in.

Building Towers

In this task, children will explore 3D shapes when selecting which shapes to use in their tower.

Shapes in the Bag

In this task, children put their hands into a bag and describe what shape they think they can feel and why.

Paper Patchwork 1

Can you work out what shape is made when this piece of paper is folded up using the crease pattern shown?

Paper Patchwork 2

Have a go at making a few of these shapes from paper in different sizes. What patterns can you create?

Paper Partners

Can you describe a piece of paper clearly enough for your partner to know which piece it is?

Always, Sometimes or Never? KS1

Are these statements relating to calculation and properties of shapes always true, sometimes true or never true?

Triangle or No Triangle?

Here is a selection of different shapes. Can you work out which ones are triangles, and why?